企业内训课程考勤管理的博弈论分析

作者简介：舒晓康（1987— ），男，汉族，四川渠县人，经济师。主要研究方向：企业管理。

摘 要：本文以博弈论为分析视角，通过构建“缺勤——点名”博弈模型，试图分析企业内部培训中的缺勤现象，借由求解模型进一步揭示“激励的悖论”是参训者缺勤的主要原因，并探讨解决问题的可能方法。

关键词：企业内训;“缺勤——点名”博弈模型;激励的悖论

在现代企业中，对员工的教育培训不可或缺。企业内部自主开展的培训，由于其有别于学校教育的特点，更为普遍地存在缺勤问题。缺勤不仅影响课堂效果，浪费大量资源，困扰着主办方同时也影响员工心态。笔者从事企业管理工作，也有主讲内训课程经验，发现参训员工缺勤原因众多，但从博弈论视角看，内训评价机制存在“激励的悖论”是员工“從容”甚至“疯狂”缺勤的主要原因。所谓“激励的悖论”，是指政策、制度的目标与其执行效果出现不一致的现象。鉴于此，单纯强化签到点名难以解决问题。

一、“缺勤——点名”模型建立

从实践中看，主办方或内训师为保证培训质量，考察出勤率的方法有：纸质签到、手机签到、随堂拍照、随机点名等;参训者出于工学矛盾等原因缺勤，又想拿到学分完成任务避免惩罚，逃避考勤的花样有：请人代签、转交手机、电召即回、替人应答等。

为方便研究，本文简化情形，用典型行为代表博弈双方策略，仅以“缺勤——点名”建立模型。模型由诺贝尔经济学奖得主、博弈论专家塞尔顿原创，他1996年在上海演讲时提出“警察——小偷”博弈模型。

在“缺勤——点名”博弈模型中，博弈方有两个：内训师和参训者。内训师针对参训者缺勤的策略集是“点名，不点名”，后者相应形成“缺勤，不缺勤”的策略集。

假设内训师点名，参训者不缺勤。对内训师而言，保证课堂出勤率并完成教学内容是其义务，参训者来上课，若不考虑心理上的成就与满足，内训师无其他实际效用，因此得益记为0;对参训者而言，若身在课堂心在外，也近似于没有得益或损失，得益同样记为0。

假设内训师点名，参训者缺勤。参训者由此受到一定处罚，比如该门课程学分为零，定期内部通报批评，甚至影响部门绩效，那么缺勤对参训者而言具有负效用，记为得益-M;内训师效用不变，得益记为0。

假设内训师不点名，参训者不缺勤。内训师认真履行了自身职责获取一定课酬，参训者按要求完成培训任务，不考虑精神收获的前提下，两者都无特别收益或损失。但值得加以注意的是，由于内训课程时间紧凑，参训者人数众多，内训师如果每节课都要点名时间成本过大，也势必影响其教学计划进度，扰乱其上课心情。因此如果内训师不点名，参训者不缺勤，对于内训师来说省时省力，因此有一定正效用。所以在这种策略组合下，内训师得益记为N;参训者得益记为0。

假设内训师不点名，参训者缺勤。参训者可以挤出时间做自己的事，比如完成本职工作避免加班，获得一定正效用，得益记为Z;而因不点名参训者没来上课，则内训师存在一定程度的“失职”行为，可能被理解成缺乏应有责任心，其教学效果和教学评价可能受到一定影响，存在一定负效用，得益记为-A。

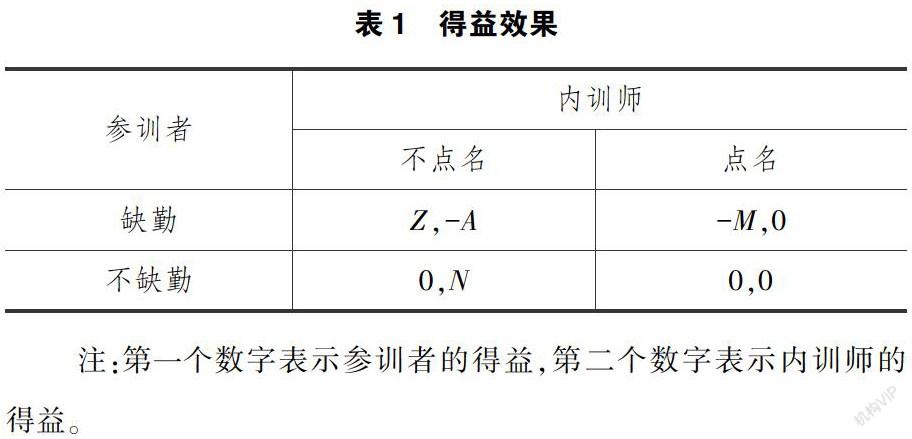
据以上分析，得益矩阵如下表1：

通过划线法、箭头法消除严格下策，显然无法得到“缺勤——点名”模型的纳什均衡解。这是一个严格竞争博弈，内训师与参训者作为博弈双方，只有竞争而没有合作的可能：若内训师的策略是点名，则参训者的策略是不缺勤;若参训者不缺勤，则内训师不点名;若内训师不点名，则参训者的策略是缺勤;若参训者缺勤，内训师又会点名，循环往复……内训师与参训者永远是猫和老鼠的关系。当然，在这一模型中，内训师和参训者事先不会通气，即不能让对方预先知道自己策略，必须随机选择。这便要引入混合策略分析法，在无法找到纯策略纳什均衡的情形下，至少可在此模型中找到一个混合策略纳什均衡的解。

二、模型的几何法（Geometic Method）求解

首先讨论参训者在缺勤或不缺勤两种策略选择的概率。

如图1所示，横轴表示参训者缺勤概率Pt，它分布在0到1之间，参训者不缺勤的概率则为1-Pt。纵轴则反映对应于参训者缺勤的不同概率，内训师选择不点名策略所获得期望值。设内训师得益为Ut，则Ut与Pt之间存在如下线性关系：

图1中从N到-A的连线即是这种线性关系反映，表示在横坐标对应的参训者缺勤概率下，内训师选择不点名的期望得益。不难看出，该线与横轴的交点Pt1就是参训者缺勤的最佳水平，参训者选择不缺勤的最佳概率是1-Pt1。首先，从N到-A连线上每一点的纵坐标就是在参训者选择该点对应横坐标表示的缺勤概率时，内训师选择不点名的期望得益N-（N+A）*Pt。假设参训者缺勤的概率大于Pt1，此时，内训师不点名的期望得益必定小于0，因此出于理性肯定选择点名，而参训者缺勤一次就要被“逮到”一次，完全没有正效用可赚。因此对参训者来说，选择大于Pt1的概率缺勤不可取。反之，若参训者缺勤概率小于Pt1，则内训师期望得益大于0，内训师每一次上课都不点名就是合理的，即使此时参训者提高一些缺勤概率，只要不大于Pt1，内训师就不会选择点名，因此参训者就不用担心被“逮到”。因为参训者在保证不被“逮到”前提下，缺勤概率越大收获就越大，因此他们会使缺勤概率趋向于Pt1，均衡点就是参训者分别以Pt1的概率选择缺勤，以1-Pt1的概率不缺勤。此时内训师点名与不点名期望得益都为0，选择纯策略点名与不点名或混合策略的期望得益都是相同的。不过事实上，为不让参训者有机可乘，内训师也必须选择自己特定概率分布的混合策略。

内训师选择点名与不点名混合策略概率分布，也可以用同样方法来确定。得出的结论就是图2中Pd1和1-Pd1是内训师最佳概率策略选择。

三、由模型得到的启示

本文“缺勤——点名”模型之间的混合策略博弈，实质上揭示了“激励的悖论”现象。