近31年中国近海潮位潮流数据库的建立及极值分析

赵建春,赵生校,赵朝志,张 哲,时 健*,童朝锋

(1.浙江省深远海风电技术研究重点实验室,浙江 杭州311122;2.中国电建集团华东勘测设计研究院有限公司,浙江 杭州311122;3.河海大学 港口海岸与近海工程学院,江苏 南京210098)

在全面推进能源生产和消费革命,构建清洁低碳、安全高效的能源体系的政策背景下,我国的海上风电事业发展迅速,海上风电场工程建设前期对潮位、潮流等海洋水文环境动力参数精细化评估成果的需求也呈现出逐步扩大趋势。潮位极值通常可以由观测数据加以分析得到[1-3],然而我国沿海的已建长期潮位站空间分布相对稀疏且一般分布在近岸区域,海上风电建设区域的潮汐潮流长时间资料数据往往比较匮乏。虽然基于历史遥感资料和数值模拟手段是获取海洋水文历史资料的有效手段,但由于遥感资料能够提供的水文资料种类有限(无法提供连续资料),因此基于数值模拟进行历史水文资料的模拟,并据此建立潮汐潮流数据库是十分必要的。Chiri等[4]以比斯开湾为例,采用ROMS数值模型方法,建立了29 a(1985—2013年)高精度的逐时潮位和潮流数据库;Fer nández-Montblanc等[5]采用SCHISM数值模型,计算了全欧洲近40 a(1979—2018年)的高精度风暴潮潮位数据。我国海洋科学工作者也对中国沿海海域的潮汐潮流特征作了大量研究和分析[6-11]。庄圆[12]计算了潮位潮位与余水位相互独立和潮位与余水位相关两种不同情况的极值水位,通过对比得出联合概率法能够比极值法更充分地利用水位观测资料,建立的风暴潮模型模拟了1997—2017年间对舟山附近海域影响较大的21场台风过程,利用耿贝尔分布计算了该区域多年一遇的极值水位和极值增水;卞建云[13]采用ADCIRC风暴潮模型对1997—2016年共42场台风进行了计算,利用泊松-广义极值分布对江苏近海20、50、100和200 a的风暴潮增水极值进行了推算。根据前人研究,目前覆盖整个中国海域的潮位和潮流数极值研究仍然较少。因此,本研究利用平面二维潮流模型TELEMAC2D建立了中国沿近海的潮汐潮流数据库,利用实测资料对天文潮潮位和风暴潮潮位及潮流充分验证,并进一步分析了1989—2019年的潮位潮流极值分布情况。研究成果可为我国的海洋工程建设提供一定的参考。

1 台风混合风场的建立和验证

1.1 背景风场

CFSR(Cli mate Forecast Syste m Reanalysis)资料是由美国环境预报中心(National Centers f or Envir on mental Prediction,NCEP)于2010年发布的全球性、高分辨率再分析资料,包含全球1979年1月至2011年3月逐时风速资料,数据空间分辨率为0.312°。2011年4月以后美国环境预报中心的第二代气候预报系统(NCEP CFSv2)提高了风场空间分辨率,为0.204°。

1.2 Jelesnianski台风风场经验计算公式

Jelesnianski气压场模型[14]为

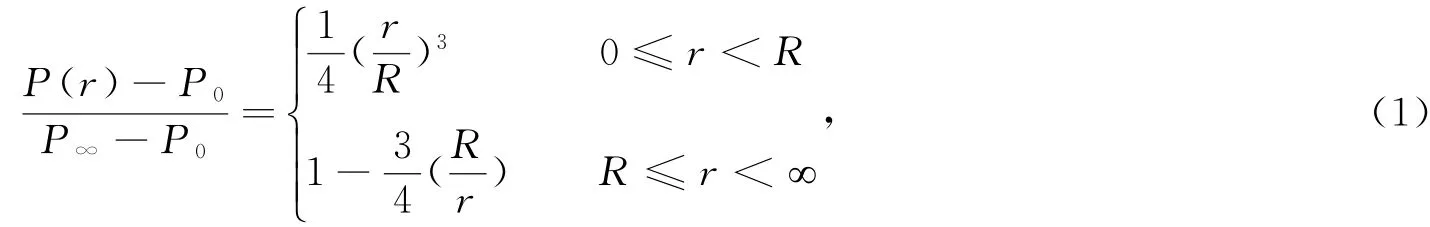
式中:P∞和P0分别为台风外围气压和中心气压,r为计算点到台风中心的距离,P(r)为模型风场气压随计算点到台风中心距离变化而变化的值,R为台风最大风速半径。

梯度风速(W )计算公式为

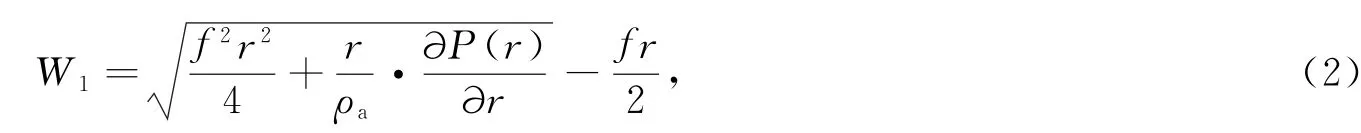
式中:f为科氏力参数,ρa为空气密度,r为计算点到台风中心的距离。

采用Jelesnianski公式获得热带气旋移行风场:

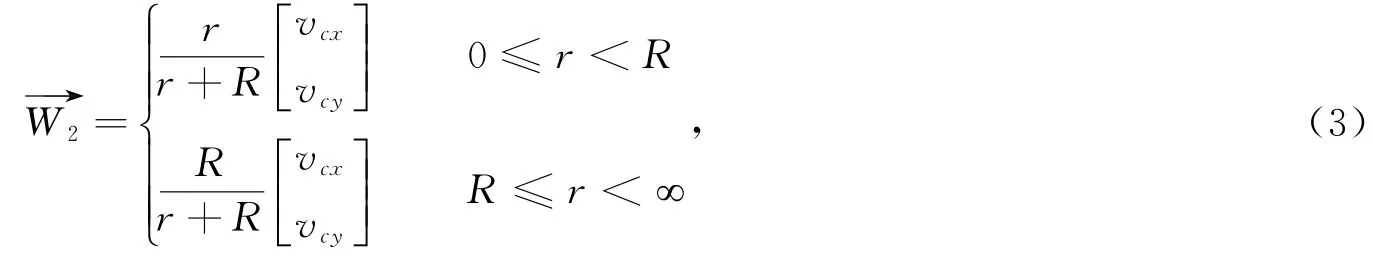
梯度风场与移行风场合成,可以得到台风风场:

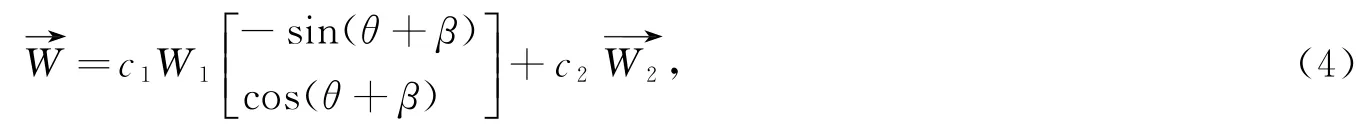
1.3 混合风场叠加方法

在台风中心附近,经验模型可较好地反映台风大风区的风场特征,但一般仅限于几百公里的范围;在台风外围,由于同时受到台风和其他天气系统的影响,风场一般与经验模型差别较大。为了改善风场模型的准确度,需要采用合适的方法将经验风场与再分析风场进行叠加。叠加方法一般有指数系数叠加法、优化半径叠加法、直接修正方法和最大风速半径叠加法。实际风场合成中发现,指数系数叠加法合成范围依赖n的取值,当最大风速半径较大时,合成区域过大,过渡带风速小于再分析风场,造成风速的不连续。优化半径叠加法难以准确确定优化半径。而直接修正法需要确定再分析风场的台风中心,这在合成过程中也难以确定。因此,本研究采用一个与最大风速半径相关的风场合成方法:

式中:VC为合成风场;VM为经验模型风场;VQ为背景风场(即再分析风场);e为权重系数。

1.4 混合风场验证结果

为验证混合风场计算精度,将台风混合风场计算的台风风速、CFSR再分析的风速、峙仔岛和滨海测风塔的风速数据进行了对比,测站位置如图1所示。

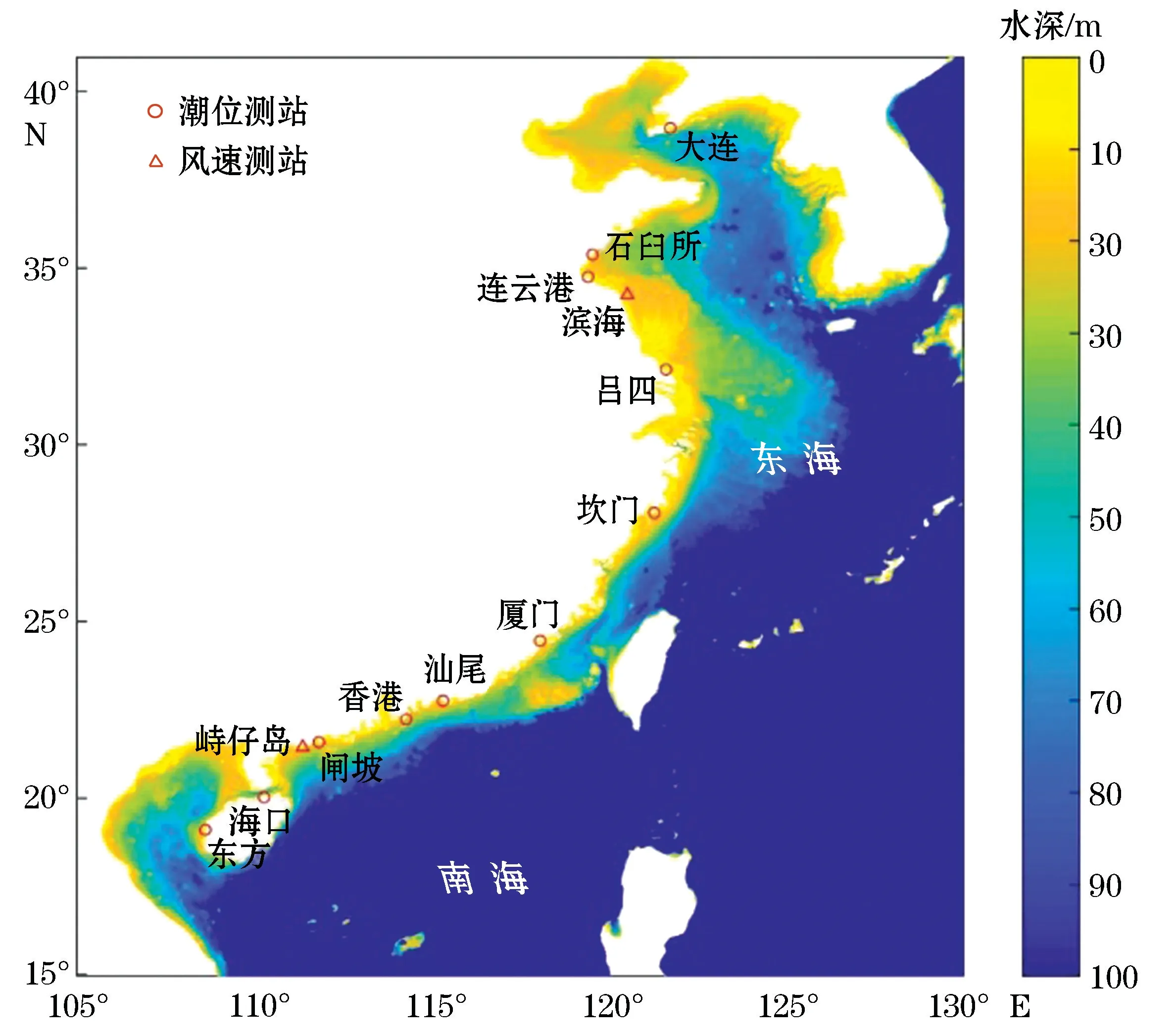
图1 潮位和风速测站位置图Fig.1 Location of the stations f or the observations of tide level and wind speed

图2 和图3分别为2008年14号台风黑格比和2012年10号达维台风期间的混合风速、CFSR风速与实测风速对比图。结果显示,CFSR再分析风场难以准确计算台风引起的风速急剧增大,存在台风期间风速偏小的情况,采用Jelesnianski台风风场经验公式计算得到的混合风场可以明显提高台风风速计算精度。

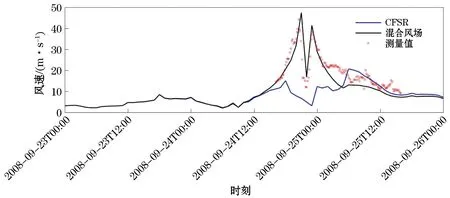
图2 峙仔岛测站2008年9月0814号台风黑格比风速对比Fig.2 Co mparison of the wind speeds of Typhoon Hagupit(No.0814)at the Zhizaidao station in September 2008

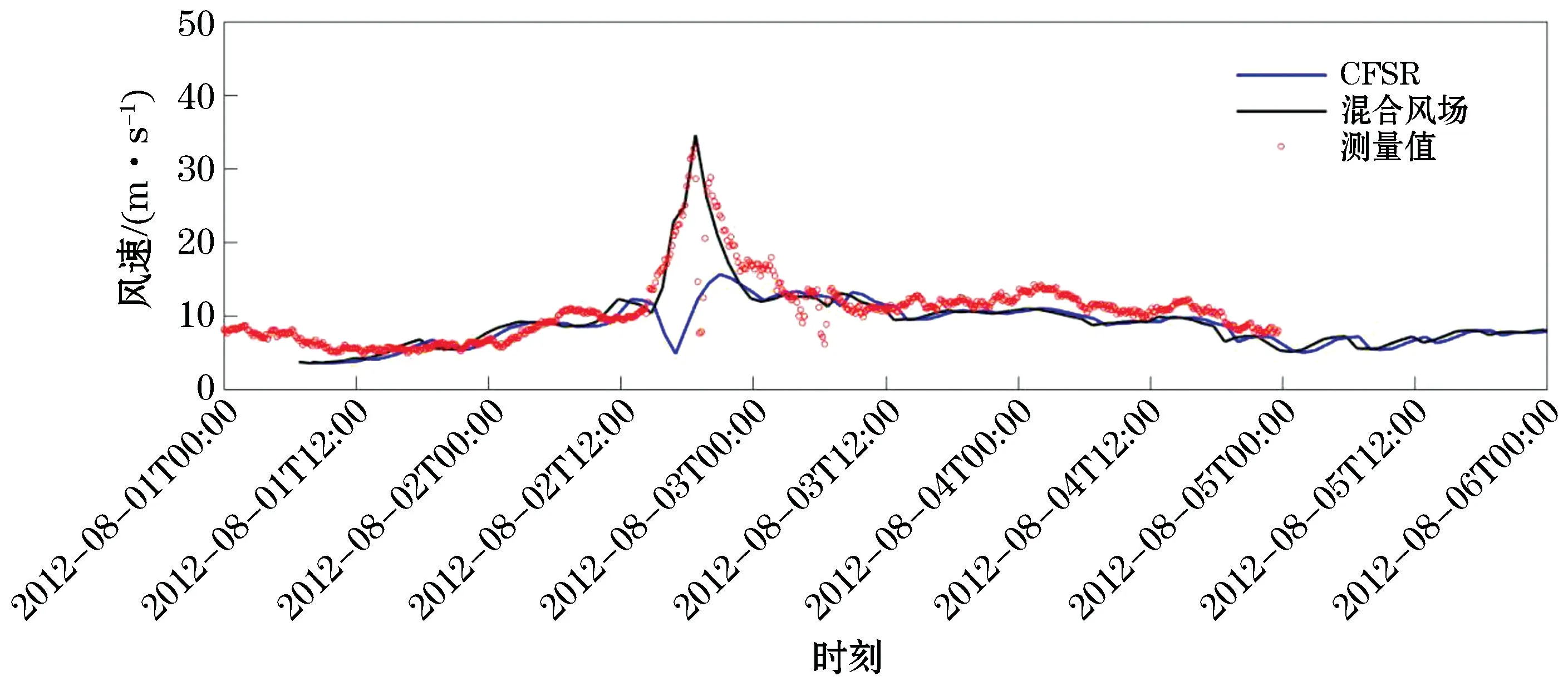
图3 滨海测站2012年8月1210号达维台风风速对比Fig.3 Co mparison of the wind speeds of Typhoon Da mrey(No.1210)at t he Binhai station in August 2012

为了进一步量化CFSR再分析风速、混合风场计算风速和实测风速的差异,采用平均偏差、相对偏差、标准差这3个统计参数来定量分析不同风速的误差(表1),计算公式如下:

表1 误差统计参数表Table 1 Statistical para meters of t he err or bet ween calculated and obser ved wind speeds

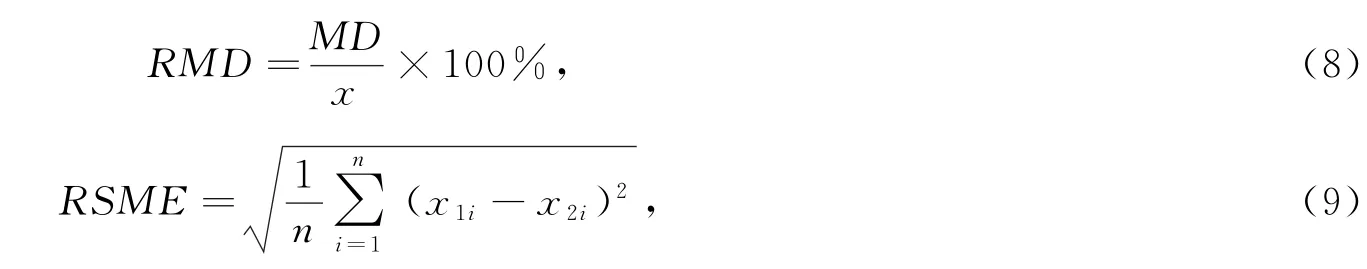
式中:MD为平均偏差,RMD为相对偏差,RMSE为均方差,n为数据点的数量,x1i为模型计算值,x2i为测站实测值。

由表1可见,CFSR再分析风速在台风期间误差较大,台风黑格比期间相对偏差近60%,而Jelesnianski模型计算出的风速与实测风速值的误差最小,台风黑格比期间相对偏差仅为-1.31%,台风达维期间相对偏差为-7.9%,说明台风混合风场可以显著提高台风期间风速精度。

2 潮汐计算

2.1 模型建立

TELEMAC2D模型是法国国家水力学与环境实验室(National Hydraulic and Environ ment Laboratory)开发的开源的河流、河口和海岸的二维水力学模型系统。模型基本方程如下:

①连续方程为

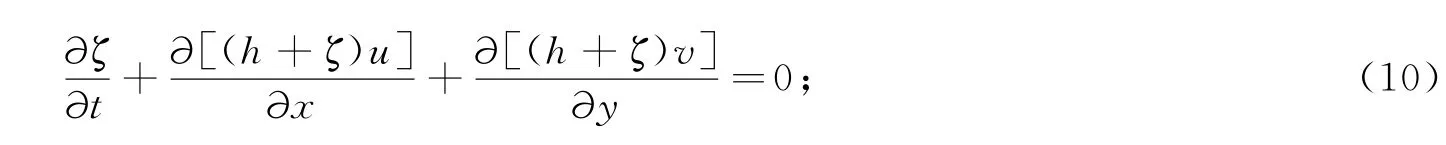
②动量方程为

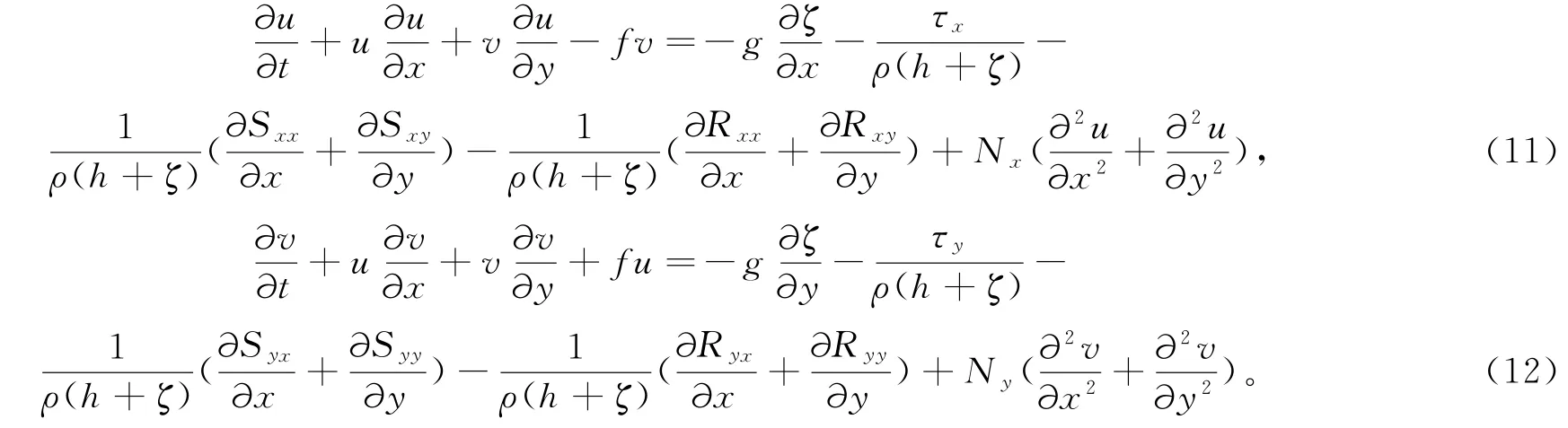
式(10)～(12)中:x和y分为直角坐标系坐标;u和v分别为x和y方向的流速分量;g为重力加速度;ρ为海水密度;Nx、Ny分别为x、y方向的水平涡动粘性系数;t为时间;f为柯氏参数;ζ为相对xy平面的水面起伏;h为静水深;Sxx、Sxy、Syx和Syy和辐射应力张量的4个分量;Rxx、Rxy、Ryx和Ryy为波浪破碎产生的切应力;τx和τy分别为波浪、潮流共同作用下的底部剪切应力矢量沿x、y方向的分量。

平面二维潮流模型网格示意图如图4所示,模型采用经纬度坐标系,共850 101个网格单元和432 516个节点。模型最大网格间距约0.5°,中国近岸研究区域网格较密,间隔约0.01°。共设置3条开边界:第1条为南面开边界,设置在印度尼西亚卡里马塔海峡;第2条设置在日本-菲律宾-印度尼西亚海域;第3条为北面开边界,设置在对马海峡和朝鲜海峡。

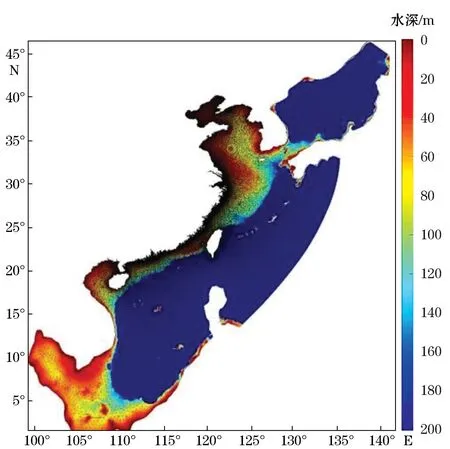
图4 模型计算区域和网格图Fig.4 The do main and grids f or t he model co mputation

2.2 模型验证

2.2.1 天文潮验证

对中国近海长期潮位站的M2和K1分潮调和常数做了验证,验证点位位置见图1,M2和K1调和常数验证结果如表2所示,分潮振幅基本在[-10,10]c m以内,分潮迟角基本在[-10,10]°以内,模型验证结果良好。此外,还对福建平潭实测潮位和潮流数据(L1～L6)进行了验证(图5和图6),验证结果显示模型能够较好地预测涨落潮流速流向,最大潮流误差为0.06 m/s(表3)。

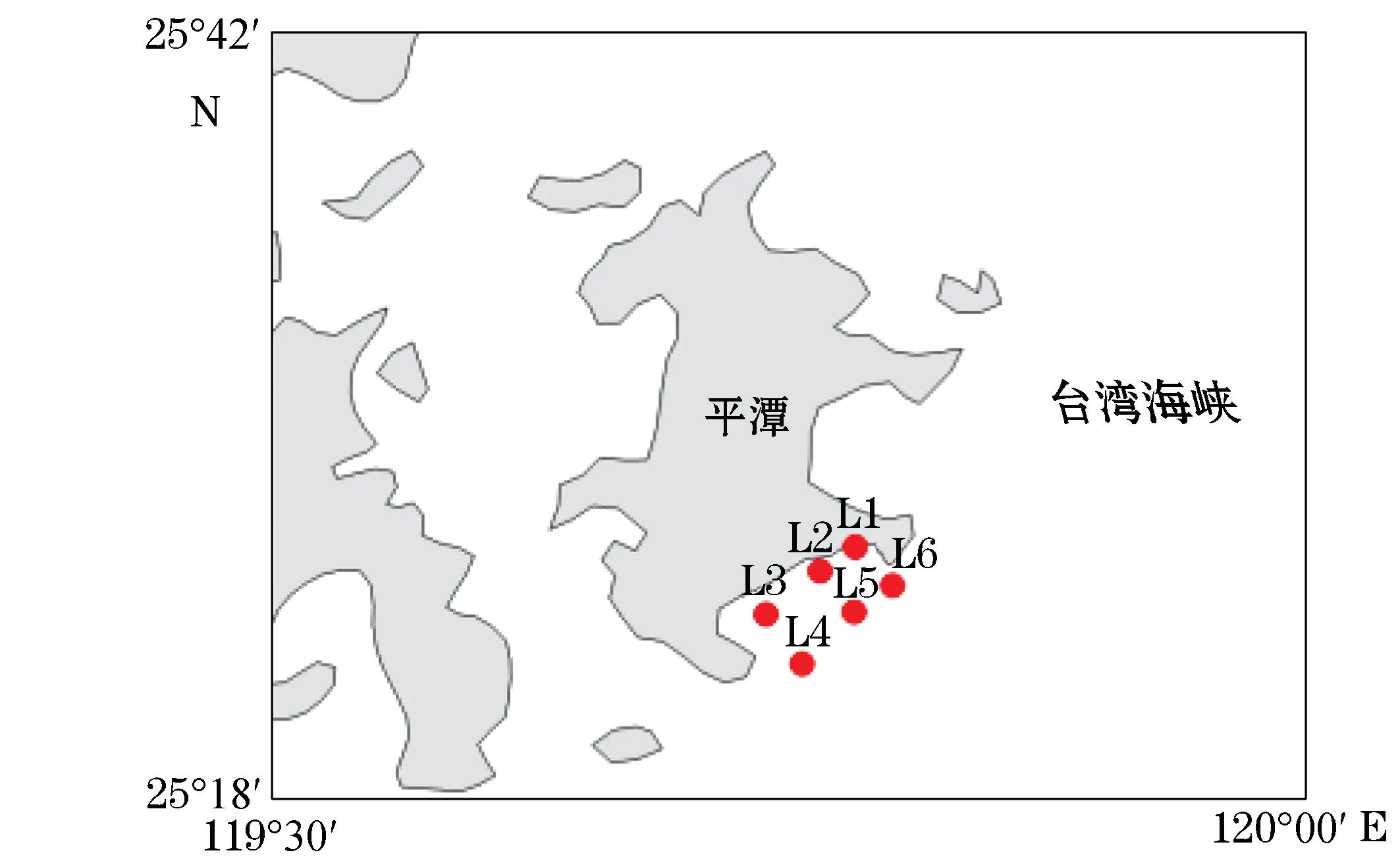
图5 2016年7月流速测站分布Fig.5 Distribution of the stations for the observations of tidal current velocity in July 2016

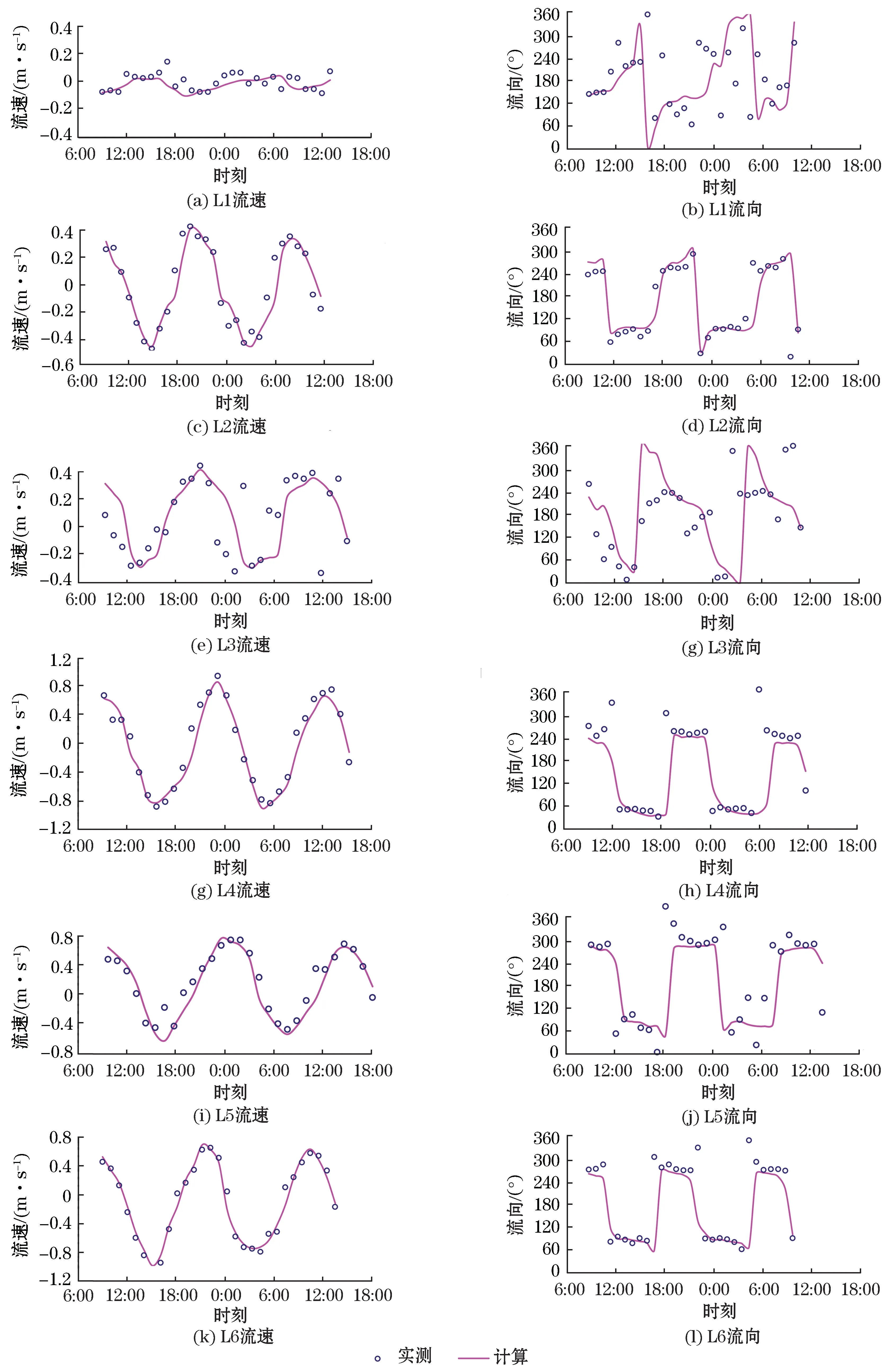
图6 2016年7月流速流向验证Fig.6 Validation of tidal current velocity and direction in July 2016

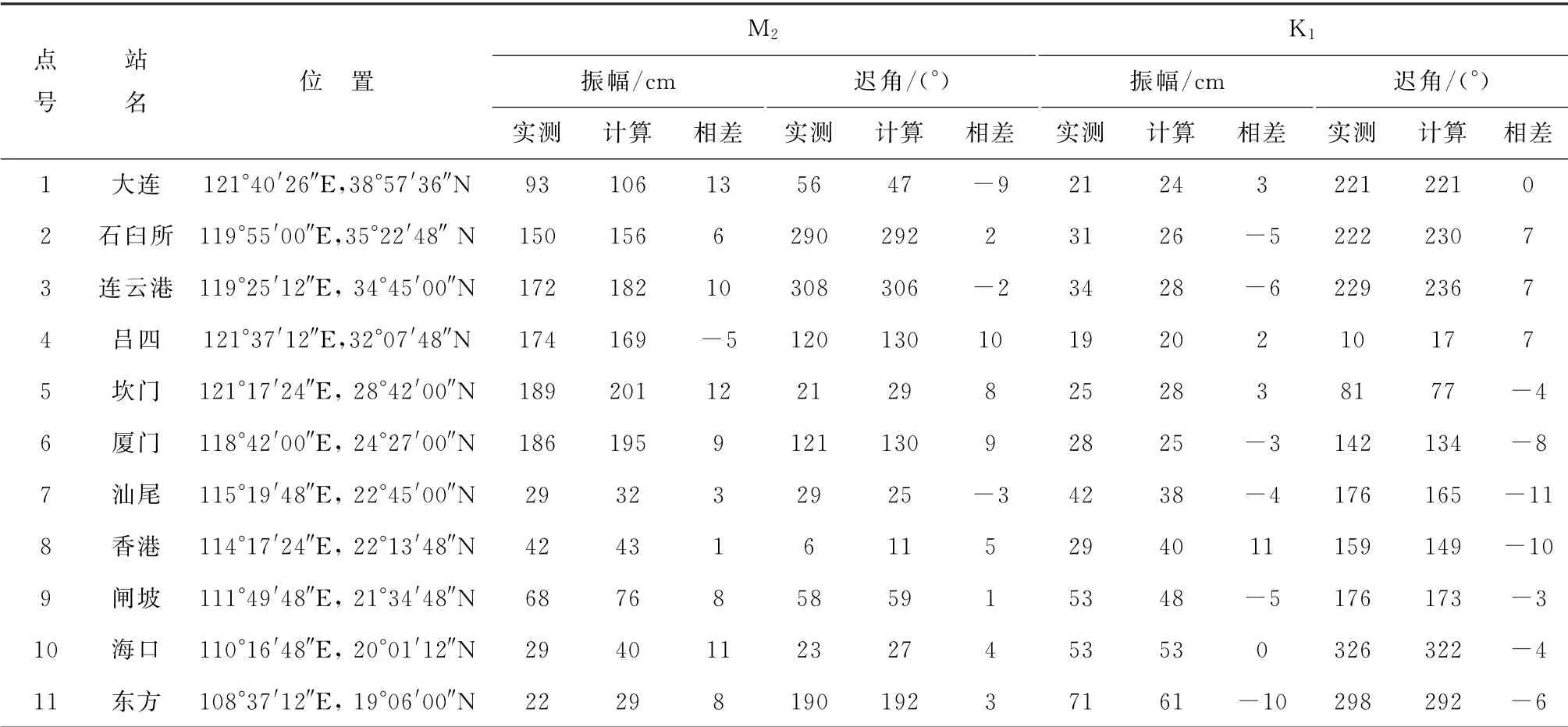
表2 中国近海模型M2和K 1调和常数验证Table 2 Verifications of har monic constants of models M 2 and K 1 in the coastal waters of China

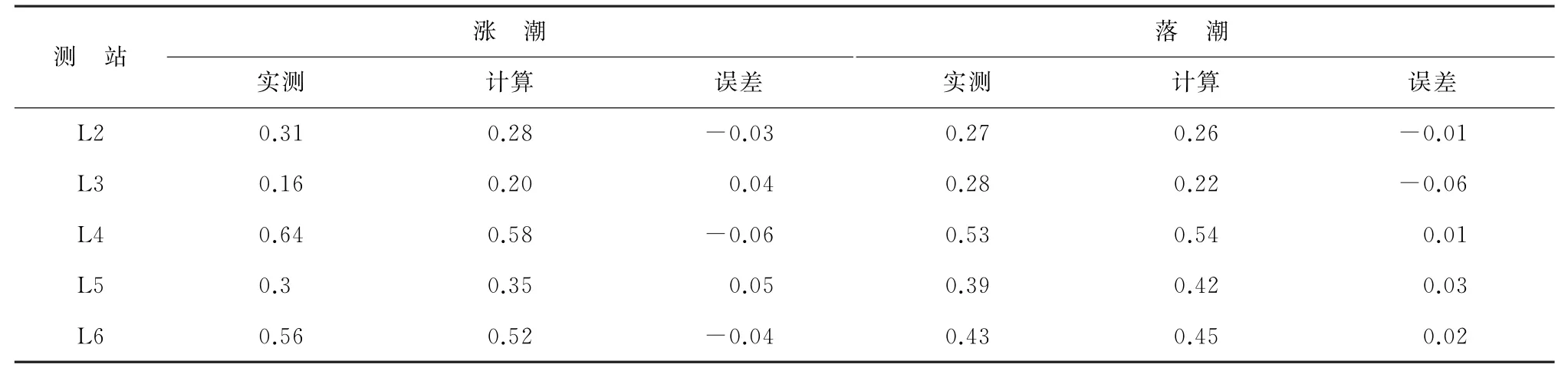
表3 平潭半潮平均流速误差参数(m·s-1)Table 3 Statistical para meters of the error bet ween si mulated and observed mean current velocities of half tide at the Pingtan station(m·s-1)

2.2.2 风暴潮验证

对盐田和惠州在“0915”和“1319”台风影响下的风暴潮位进行了验证,测站位置见图7。图8和图9分别为2次台风过程的风暴潮位验证,图中水位为相当于1985高程的水位值。结果显示,高低潮位误差在18 c m以内,验证结果相对较好(表4)。

表4 “0915”和“1319”台风风暴潮高潮位误差参数(m)Table 4 Statistical para meters of t he err or bet ween si mulated and observed high tide levels of the stor m sur ges during Typhoon No.0915 and No.1319(m)

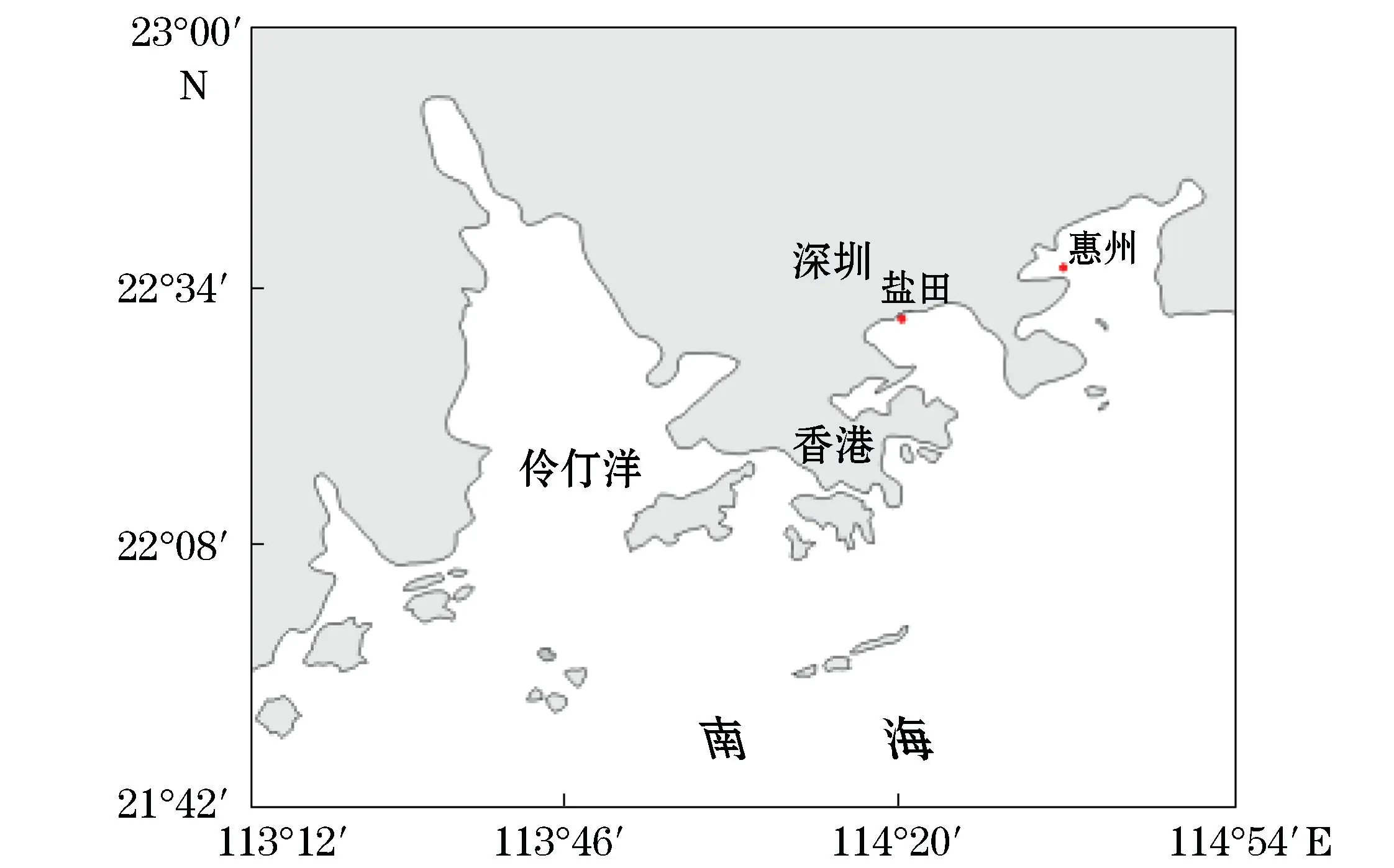
图7 潮位验证点位置Fig.7 Location of the stations for tidal level validation

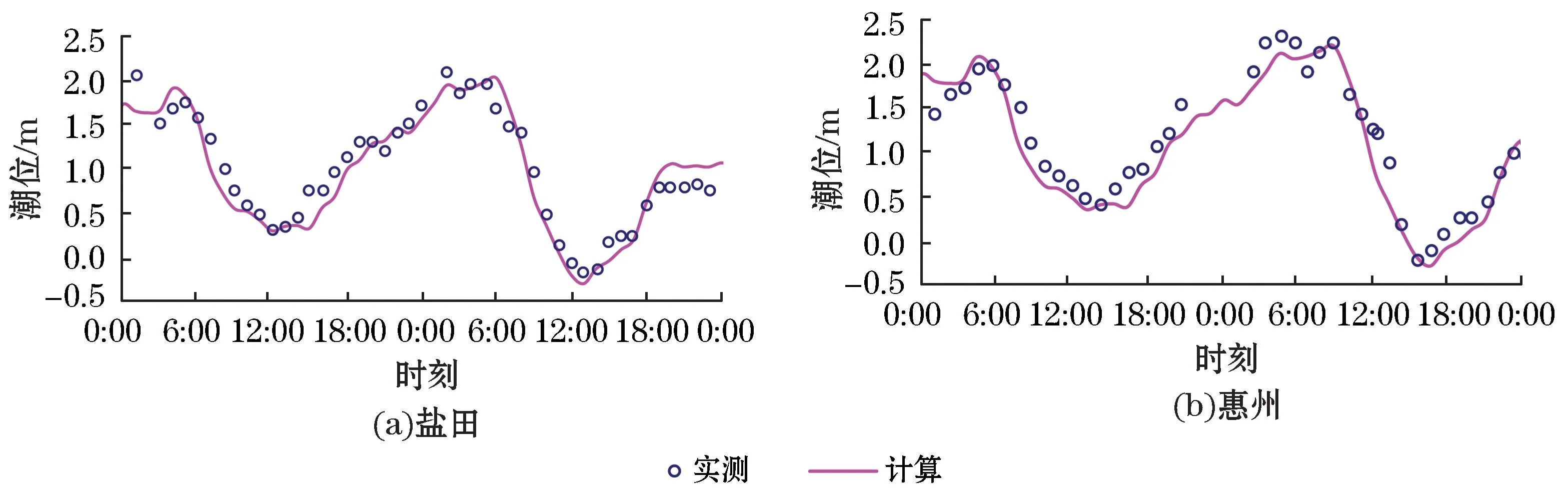
图8 “0915”台风期间潮位过程对比Fig.8 Co mparison of the tidal level processes during Typhoon No.0915

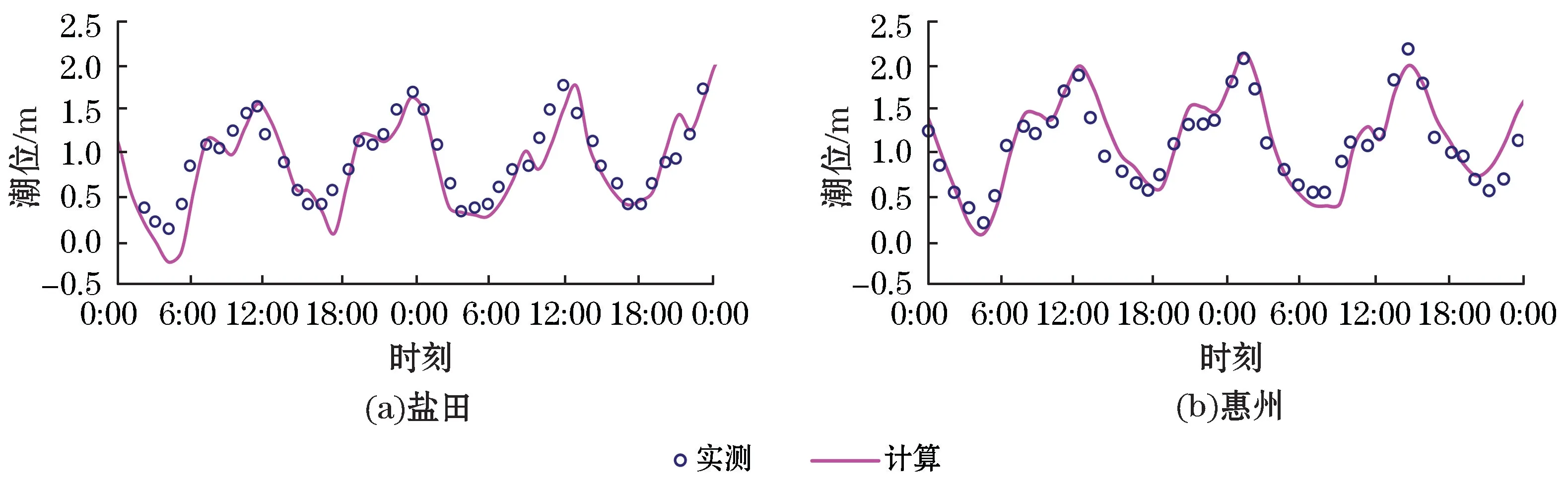
图9 “1319”台风期间潮位过程对比Fig.9 Co mparison of the tidal level processes during Typhoon No.1319

3 潮位及潮流极值分布

利用TELEMAC2D模型研究了中国沿海1989—2019年期间的逐时潮位、潮流过程。基于各地平均海平面计算得到潮位及潮流结果,提取每年的最高、最低潮位和最大流速,采用耿贝尔分布法对极值数据进行分析。

3.1 高潮位极值分布

图10为中国沿海高潮位重现期分布,中国沿海不同重现期高潮位极值主要分布在东海和南海北部,越靠近海岸高潮位越高。2 a一遇高潮位,浙江、福建近海多在2～3 m,南海远海区域略大于1 m,广东、广西近海在1.5 m左右,台湾海峡区域为3～4 m,江苏辐射沙洲区域略大于3 m。100 a一遇高潮位,浙江、福建近海在3～4 m,南海远海区域在1～2 m,台湾海峡和北部湾顶局部超过4 m,江苏辐射沙洲区域约为3.5 m,渤海老黄河口、秦皇岛、黄海山东半岛及中部海域则相对较低。

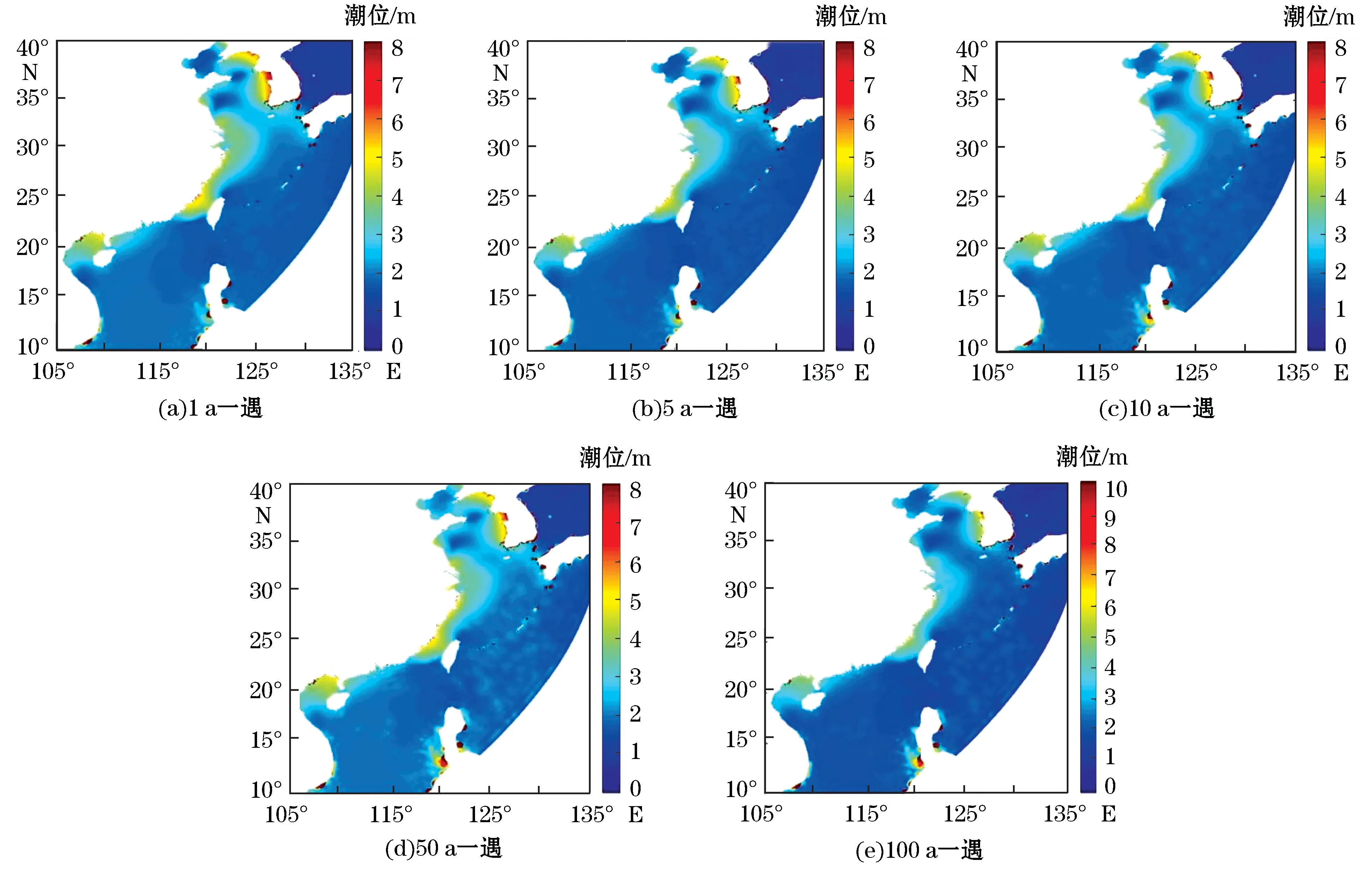
图10 中国沿海不同重现期高潮位分布Fig.10 Distributions of the high tide levels with different recurrence periods in the coastal waters of China

3.2 低潮位极值分布

图11 为中国沿海低潮位重现期分布,中国沿海不同重现期低潮位极值主要分布在东海和南海北部。2 a一遇低潮位,浙江、福建近海区域多在-2.8 m左右,台湾海峡约-4 m,浙江、福建近海区域约-3.1 m,台湾海峡区域约-4.5 m,渤海老黄河口、秦皇岛、黄海山东半岛及中部海域则相对较高。

3.3 潮流流速极值分布

图12 为中国沿海不同重现期流速大小,流速极值主要分布在潮差较大或水深较浅的区域。2 a一遇流速,黄海近岸海域多在1.2 m/s左右,浙江沿海多在1.0 m/s以下,台湾海峡南侧台湾浅滩海域局部可达2.5 m/s,南海区域多在1.0 m/s以下,北部湾口和琼州海峡流速则相对较大。100 a一遇流速,黄海近岸海域多在1.5 m/s左右,浙江沿海多在1.0～2.0 m/s,台湾海峡南侧台湾浅滩海域局部可达3.0 m/s以上,南海近岸海域一般可达1～2 m/s,北部湾口和琼州海峡流速亦相对较大。

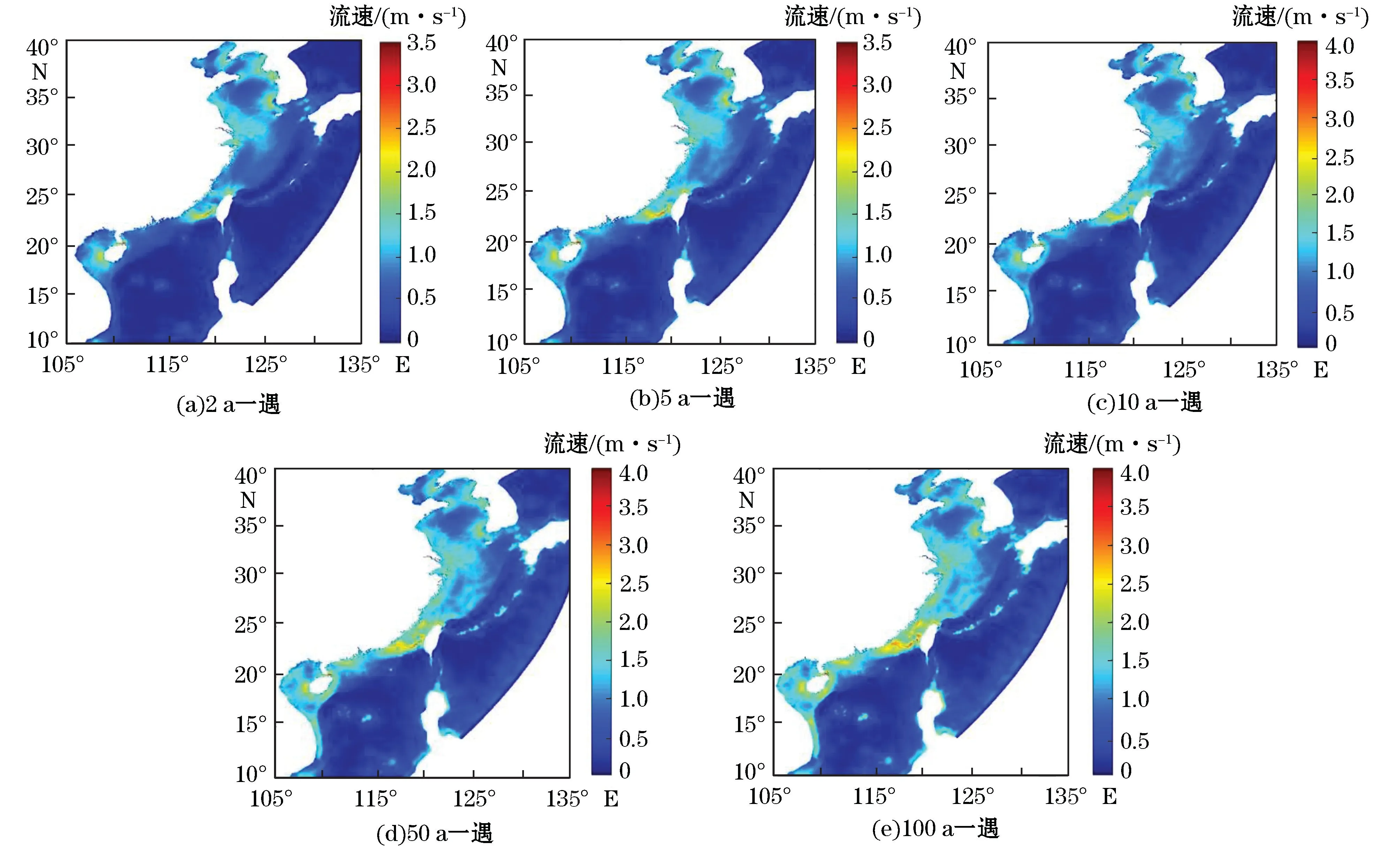
图12 中国沿海不同重现期流速分布Fig.12 Distributions of t he tidal current velocities with different recurrence periods in the coastal waters of China

4 结 语

采用TELEMAC2D模型,在基于CFSR和CFSv2再分析风场数据及经验风场建立混合风场的基础上,计算了中国近海1989—2019年的水位和流速数据,建立了中国近海高精度长时间序列的潮汐数据库。模型计算结果和实测值的误差分析显示,分潮振幅误差在[-10,10]c m以内,分潮迟角在[-10,10]°以内,最大潮流误差为0.06 m/s,模型验证结果良好。

通过模型计算建立的潮汐潮流数据库,推求得到了中国近海不同重现期的高低潮位和流速极值。结果表明,中国沿海不同重现期高潮位在东海和南海北部较高,由于风暴潮作用,越靠近海岸高潮位越高,高潮位极值较大区域主要分布在东海沿岸,尤其是台湾海峡较高,另外北部湾的高潮位极值也较大;低潮位较低区域也主要分布在东海沿岸,台湾海峡及北部湾低潮位较低。流速极值较大区域主要分布在黄海近岸、台湾海峡、琼州海峡和北部湾湾口。

本研究可用于中国沿海海岸工程设计水位和流速值的确定,为海岸风险评估和防灾减灾提供基础水文信息。