椭圆余弦波作用下海床响应特征的有限体积法数值分析*

刘小丽，刘洪睿

(1.山东省海洋环境地质工程重点实验室，山东 青岛 266100;2.中国海洋大学环境科学与工程学院，山东 青岛 266100)

在近岸浅水海域，波浪是诱发海床液化的主要原因之一，研究波浪作用下海床响应及其液化特征，对海底管线和防波堤等构筑物的安全设计具有重要意义。

对于近岸浅水区，当水深与波长之比小于0.125时，波浪特征已不再适合用斯托克斯波浪理论进行描述，此时宜利用浅水非线性波理论进行分析，而椭圆余弦波理论是最主要的浅水非线性波理论之一[1]。

Hsu等[2]对椭圆余弦波作用下海床瞬态响应特征进行了分析，结果表明，与线性波浪作用相比，椭圆余弦波作用下海床瞬态液化区的深度相对较浅，但宽度较大，这与椭圆余弦波在海床面上的波压力分布特征有关。对椭圆余弦波和线性波作用下海床瞬态响应的一系列对比研究表明，椭圆余弦波作用下海床中孔隙水压力幅值增大显著[3-6]。此外，徐云峰等[7]对椭圆余弦波作用下海床瞬态响应进行了参数分析，结果表明，海床的渗透性、剪切模量以及孔隙水的压缩性对孔压有明显的影响，而海床的渗透各向异性对孔压的影响较小。

上述研究都是针对椭圆余弦波作用下海床的瞬态响应特征，目前仍缺乏对椭圆余弦波作用下海床累积响应和渐进液化特征的分析。为此，基于开源流体力学计算平台OpenFOAM，根据有限体积法原理，利用C++语言开发了波浪作用下海床响应数值计算求解器(SeabedFoam)，并结合OpenFOAM中波浪数值模拟求解器IHFOAM[8]，对椭圆余弦波作用下海床的瞬态响应、累积响应及渐进液化特征进行分析，并通过与线性波作用下海床响应的对比，分析近岸浅水区波浪非线性的影响。

1 数值计算模型

1.1 波浪水动力模型

波浪水动力的模拟采用Higuera等[8]开发的波浪求解器IHFOAM进行计算，该求解器基于OpenFOAM平台，利用有限体积法求解。有限体积法的控制积分方程表征了求解变量在控制容积内的通量守恒，离散后方程中的每一项都有明确的物理意义，这一点对于流动和传热问题而言，是有限元等其他数值方法所不具备的，因而有限体积法是目前求解流体流动和传热问题最有效的数值计算方法，得到了广泛的应用[9]。

波浪水动力控制方程为雷诺时均N-S方程(RANS方程)：

▽·U=0。

(1)

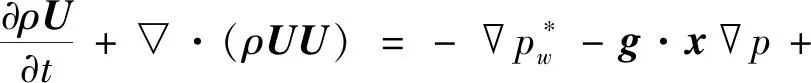
(2)

关于波浪水动力模型的详细介绍可参见Higuera等[8]的文章，此处不再赘述。利用IHFOAM模拟近岸浅水区椭圆余弦波的传播过程，可得到海床面上的波压力分布。

1.2 波致海床响应模型

图1为椭圆余弦波作用下海床响应计算模型示意图。椭圆余弦波沿x轴的正向传播，海床厚度为h，取一个波长L为水平方向计算域；水深为d，波高为H；海床底部为不透水基岩。本文重点对椭圆余弦波作用下海床的累积孔隙水压力及渐进液化特征进行分析，海床响应计算模型适用于砂土和粉土等无粘性土海床。

图1 椭圆余弦波作用下海床响应计算模型示意图Fig.1 Sketch of the computational model for seabed response under cnoidal wave

1.2.1 控制方程及有限体积法求解 波浪作用下海床响应主要体现在波压力引起的土骨架应力变形和孔隙水压力的变化。Liu等[10]提出了一种考虑波致海床累积孔隙水压力与应力耦合的简便计算方法，能较好的计算波浪作用下海床瞬态和累积响应过程。基于该模型，对海床响应控制方程进行有限体积法求解。

根据Biot弹性多孔介质理论，土体应力平衡方程为：

(3)

式中：G为剪切模量；λ是拉梅系数；D是位移矢量；I为单位矩阵；tr表示矩阵的迹；ps为孔隙水压力。

将方程(3)显性项和隐性项分离，这种方法可以提高收敛性并减少计算时间，即：

▽·[(2G+λ)▽D]=▽ps-▽·[G(▽D)T+λItr(▽D)-(G+λ)▽D]。

(4)

方程(4)的左手项为：

(5)

式中的梯度项采用隐式离散方法，利用结构化网格：

(6)

式中下标f、N、P分别代表面心以及面两侧单元体中心，为两个单元体中心的距离，s为面向量。

根据Liu等[10]，土体渗流连续控制方程为：

(7)

方程(7)的右手项为土骨架体积应变率；ks为渗透系数；γw为水体重度；n为孔隙率；mv=(1-2μ)/G，为土骨架体积压缩系数；ψ为波致循环剪切应力引起的孔隙水压力增长速率：

(8)

α=0.34Dr+0.084;β=0.37Dr-0.46。

(9)

βs是孔隙流体压缩系数，表达式为：

(10)

式中：Kf为水的体积压缩模量；Sr为饱和度；pow为绝对静水压。

方程(7)左手项隐式离散，右手项显式离散，位移矢量D为前一步计算所得位移值，第一个时间步位移D为零。

在有限体积法框架下，采用应力平衡方程和渗流连续方程分离求解的策略，具体可参见文献[11-12]。

1.2.2 模型边界条件 海床上表面竖向有效正应力和剪应力为0，在OpenFOAM中通过施加Neumann边界实现这一条件：

(11)

式中：t为海床表面作用力，此处为0。此外，海床上表面的孔隙水压力为波浪在海床面上的波压力。对于椭圆余弦波，其波压力通过水动力模型进行数值计算得出；而对于线性波浪，则直接利用海床表面线性波压力的解析解计算，具体为：

pb=p0cos(kx-ωt)。

(12)

式中：pb为海床表面波压力;p0=(γwH)/[2cosh(kd)]为海床表面波压力幅值；ω=2π/T为波浪圆频率；k=2π/L为波数。

两侧采用周期性边界条件。底部为不透水边界，孔压梯度和位移为零：∂ps/∂z=0,u=w=0。

2 数值计算模型的验证

2.1 水动力模型验证

波浪水动力模型(IHFOAM)模拟结果的可靠性已经过大量实验数据和解析结果的验证[13-14]。此处对数值模拟椭圆余弦波传播过程的适用性进行验证，将数值模拟结果与Chang等[15]波浪水槽试验结果进行对比。波浪水槽试验中分别测量了距离造波板4.8和13.2 m处椭圆余弦波的波面高度，波浪参数为：波高3.6 cm，水深24 cm，周期2 s。

椭圆余弦波的波面计算值与试验值对比结果如图2中所示。从中可以看出，水动力模型的计算结果与试验结果较为一致，可用IHFOAM对椭圆余弦波传播过程进行模拟计算。

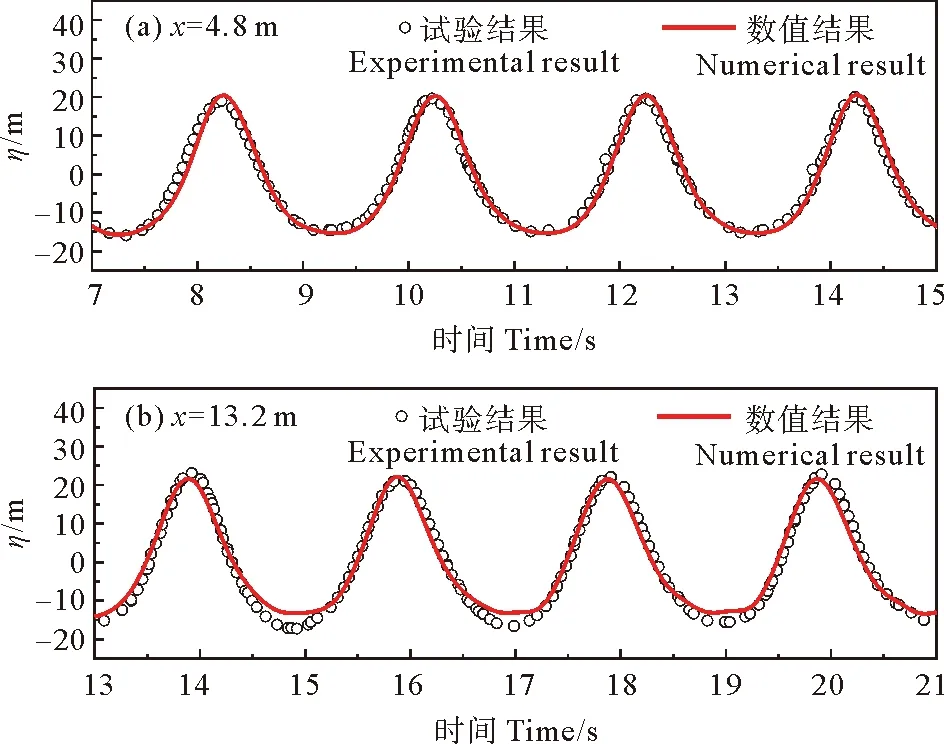
图2 椭圆余弦波数值结果与试验结果[15]对比Fig.2 Comparison of numerical and experimental results[15] for cnoidal wave propagation

2.2 海床响应模型验证

通过与Sumer等[16]进行的波浪水槽试验结果对比，验证数值模型计算结果的正确性。采用与试验中相同的波浪海床计算参数，其中波浪参数为：水深0.55 m，波高0.18 m，波浪周期1.6 s，波长3.18 m；海床参数见表1。

表1 水槽试验中海床参数Table 1 Seabed parameters in flume experiment

图3为数值模型计算结果与试验结果的对比，从中可以看出波浪作用下数值模型计算得到的孔隙水压力随时间变化趋势与试验结果较一致，表明了基于有限体积法计算海床响应的数值计算程序的可靠性。

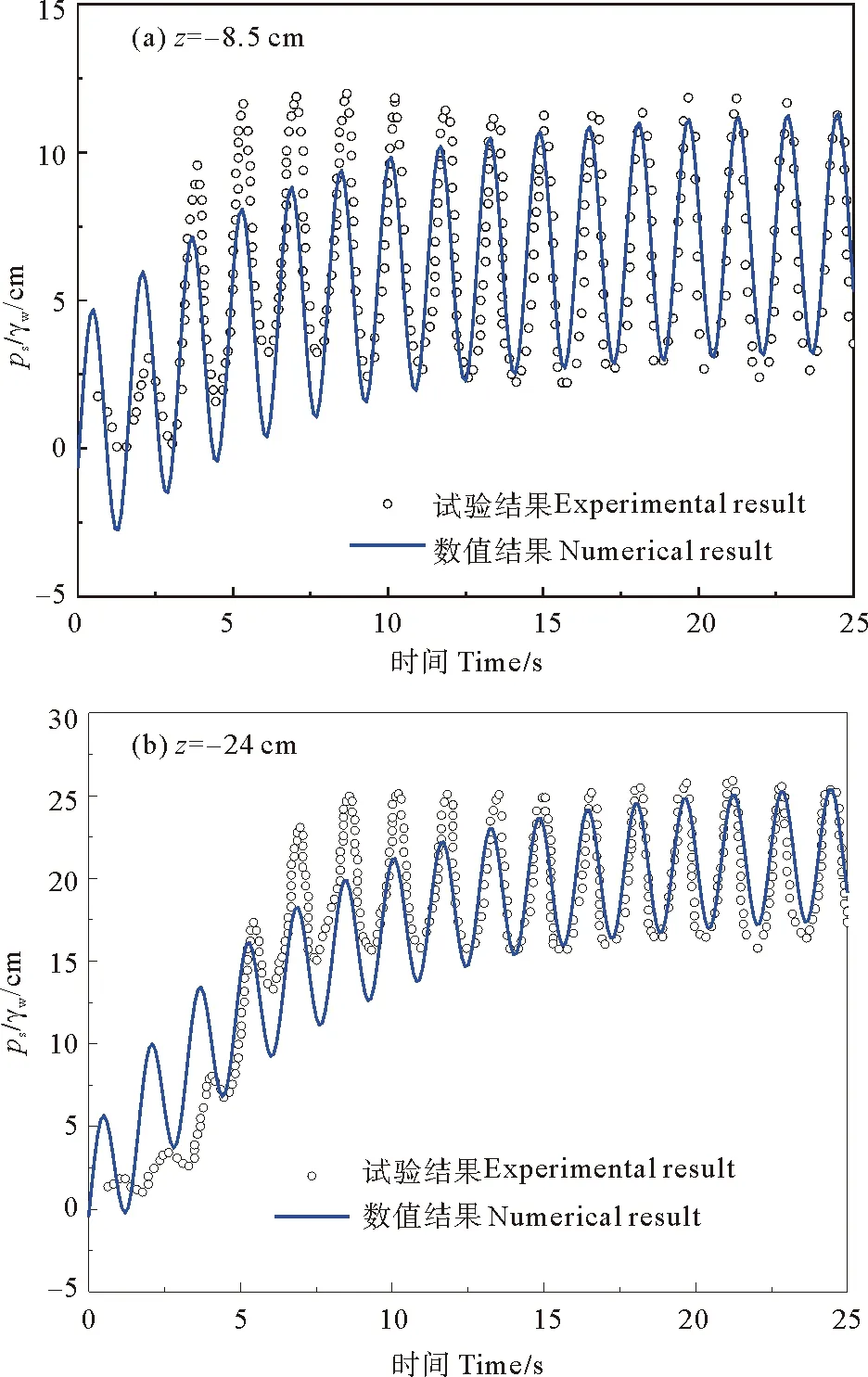
图3 海床孔压数值结果与水槽试验结果[16]对比Fig.3 Comparison of numerical and experimental results[16] for seabed pore water pressure

3 结果与讨论

对椭圆余弦波作用下海床瞬态响应、累积响应和液化特征进行分析，并与线性波结果进行对比，分析近岸浅水区波浪非线性的影响。具体计算参数如表2中所示。

表2 波浪和土体参数Table 2 Parameters of wave and seabed

3.1 海床瞬态响应

如图4所示，为海床表面椭圆余弦波的波压力与线性波的波压力对比图。从图中可以看出，一个周期内，相对于线性波浪，椭圆余弦波的波压力分布表现为波峰更为尖锐，波谷则相对平坦，其波压力幅值较线性波压力的幅值高出约40%，波压力最大值和最小值的绝对值相差较大，表面波压力为正值的持续时间小于波压力为负值的持续时间，这种时空非对称性会直接影响海床孔压响应特征。

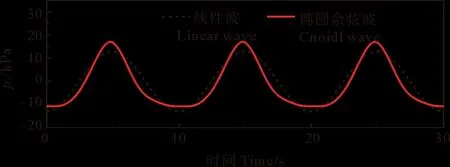
图4 椭圆余弦波波压力与线性波波压力对比图Fig.4 Comparison of cnoidal wave pressure and linear wave pressure

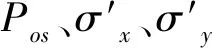
图5 海床瞬态响应变量沿深度分布图Fig.5 Distribution of transient seabed variables along depth

通过表面波压力的时空分布可以发现，椭圆余弦波的波峰作用时间相对于线性波较短，而波峰对应的最大波压力却远大于线性波，这导致在椭圆余弦波向岸传播过程中，特别是波谷向波峰变化的时间段内，海床表面对应的瞬时压力梯度增大，这些都是导致椭圆余弦波非线性效应显著的重要因素。

3.2 海床累积响应与渐进液化

试验研究表明，对于松砂或中等密实度的砂质或粉质土海床，当其渗透系数较小时，在波浪循环荷载作用下海床内的超静孔隙水压力会不断累积，当某点的超静孔隙水压力达到其上覆有效应力时，即会引起该深度海床的液化[15-16]。对椭圆余弦波作用下海床孔压累积和液化特征进行分析，液化判别准则为[17]：

ps-(γ′z+pb)>0。

(12)

图6分别为距海床面1、4和8 m深度处海床中孔压随时间变化曲线，从图中可以看出，椭圆余弦波作用下孔压累积速度明显快于线性波。1 m深度处，1 000 s时累积孔压相较于初始时刻增长了50%，其中0～200 s 增长速度最快，孔压增长了35%，900 s以后孔压不再增长；而线性波作用下孔压累积缓慢，1 000 s时孔压增幅不到10%。波浪作用100个周期时，椭圆余弦波作用下海床的累积孔压约是线性波作用下的3倍。

从图6中可以看出，椭圆余弦波作用下海床孔压累积速率明显快于线性波作用下海床孔压的累积速率，这进一步导致了椭圆余弦波和线性波作用下海床液化区发展的差异。

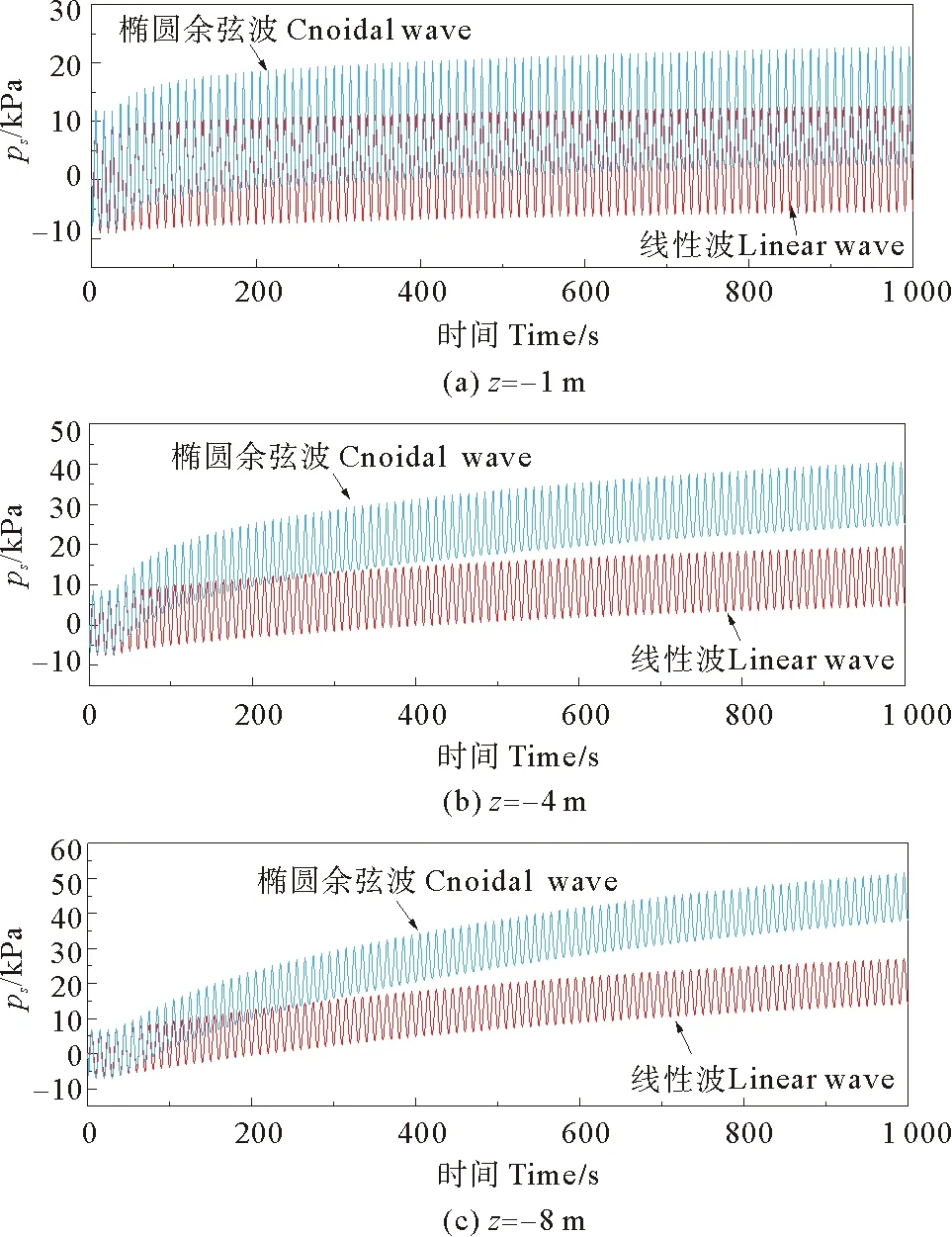
图6 孔压随时间发展变化图Fig.6 Development of pore water pressure over times

如图7所示，为椭圆余弦波作用下海床液化区在不同波浪作用时间的分布图。从椭圆余弦波导致的液化发展图中可以看出，液化首先发生在波谷区，25个波浪作用周期时的海床最大液化深度为1.05 m。随着时间的推进，液化区逐渐向水平和深度方向发展，50、100和200 T时对应的最大液化深度分别为2.38、3.64和4.98 m，最大液化深度发展速率呈逐渐减缓的趋势。当前算例中，线性行进波作用下孔压增长缓慢，波浪作用200个周期时海床仍未发生液化。

图7 椭圆余弦波作用下海床液化区分布图Fig.7 Cnodial wave-induced seabed liquefied zone

线性波浪荷载引起的海床剪应力相对较小，而椭圆余弦波具有较强的非线性，其波致海床循环剪应力幅值相对较大，能够显著促进海床中累积超静孔隙水压力的发展。椭圆余弦波的波峰尖锐对应的海床表面波压力幅值较大，引起向下的渗流，导致波峰作用处海床相对较难液化，而波谷处波压力引起向上的渗流，随着累积孔隙水压力的不断发展，其液化深度发展较为显著。

从孔压累积发展过程和液化区分布特征可以看出，浅水区波浪的非线性效应对于海床累积响应表现得更为显著。

4 结语

基于OpenFOAM开源流体力学计算平台，利用C++语言开发了波致海床响应的有限体积法数值计算程序，通过与试验结果的对比，验证了数值计算程序的可靠性。

对椭圆余弦波和线性波作用下海床响应和液化特征的计算分析表明，椭圆余弦波作用下海床瞬态孔压和应力幅值明显偏大，瞬态孔压差异可达30%，剪应力差异可达40%。剪应力的差异进一步导致海床累积孔压和液化区的显著差异，波浪作用100个周期时，椭圆余弦波作用下海床累积孔压约为线性波作用下累积孔压的3倍。

近岸浅水区波浪的非线性效应明显，特别是对细砂或粉质土海床累积孔隙水压力和液化区的发展，其影响尤为显著，不容忽视。