基于主动安全的改进人工势场局部路径规划研究
张三川, 明 珠
(郑州大学 机械与动力工程学院,河南 郑州 450001)
0 引言
局部路径规划是解决车辆主动安全问题的重要途径之一[1],具有实时性强、计算效率高的显著特点[2]。目前局部路径规划算法主要有A*算法[3]、遗传算法[4]、蚁群算法[5]、粒子群算法[6]和人工势场法[7]等,其中人工势场算法具有结构简单、信息处理速度快、实时性好、路径光滑等优点。但传统人工势场法容易出现局部极小值和目标不可达等问题[8],国内外学者对此提出了不同的方法加以改进。Fedele等[9]引入了螺旋势场,利用目标引力场和螺旋势场之间的切换策略,使实验小车能够绕过障碍物。Rostami等[10]通过寻找成本函数,引入调节器对斥力函数加以修正,成功解决了局部极小值问题。Raheem等[11]应用粒子群优化算法寻找人工势场因子的最佳值,提出了基于迭代优化的改进混合路径规划方法。郭枭鹏[12]引入广义虚拟势场概念,构造了一种使实验车辆沿势场函数下降方向运动的势场模型。徐小强等[13]针对自行式机器人,基于安全距离概念,引入预测距离算法使机器人陷入局部极小值之前能做出反应,并用设置虚拟的目标点的方法来引导机器人脱离极小值。宣仁虎[14]提出了修正势场,对人工势场法存在的目标不可达和局部极小值问题引入逃逸力进行改进。刘志强等[15]建立了道路边界危险斥力模型,并在障碍物斥力场中引入速度因素,通过求解平衡方程来获取安全路径。
鉴于相关文献对传统人工势场理论改进方式较为单一,本文拟引入调节因子与附加力,从两个方面对传统人工势场加以改进;同时,综合各改进算法的特点,建立以时效性与安全性为主要评价指标的价值函数模型,以期为自动驾驶技术开发提供基础理论支持。
1 改进人工势场
1.1 传统人工势场
当实验车位于路径规划区间时,会受到如图1所示的障碍物斥力和目标点引力,并始终在引力和斥力的耦合作用下实现避障前行。目标点产生的引力势场Uatt(M,Mg)用实验车与目标点之间距离S(M,Mg)和引力增益系数α来表达:
(1)
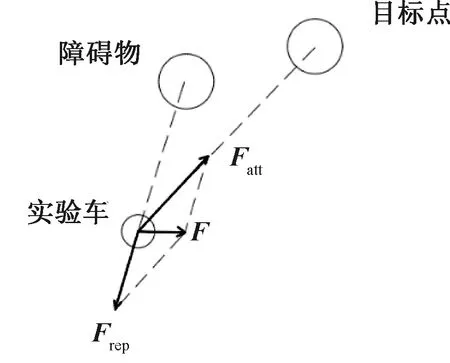
图1 传统人工势场Figure 1 Traditional artificial potential field
本文为纯数学模型,除仿真时长外所有参数均无量纲。
目标点对实验车所产生的引力方向始终指向目标点,其大小为引力势场(式(1))的负梯度:
Fatt(M)=-gradUatt(M,Mg)=-αS(M,Mg)。
(2)
当实验车辆进入障碍物作用范围内时,障碍物会对其产生斥力,斥力场函数Urep为
(3)
式中:β为斥力增益系数;A为斥力作用的判断参数,计算式为
(4)
式中:S(M,Mobs)为实验车与障碍物之间的距离;S0为斥力场作用半径。
实验车所受斥力Frep(M)为斥力场的负梯度,大小为
(5)
若实验车受到多个障碍物的同时作用,其所受总斥力为各障碍斥力的矢量和:
(6)
显然,传统人工势场下的实验车所受到的引力与斥力的合力为
(7)
如图2(a)所示,当障碍物与目标点间的距离过于接近时,目标点产生的引力可能会小于斥力,此时,合力方向与前进目标点方向相反,即出现实验车反而远离目标点的不可达问题。如图2(b)所示,当实验车、障碍物和目标点3者共线时,引力与斥力还可能相互抵消而出现合力为0的情况,出现局部极小值问题。

图2 传统人工势场的2种特殊情形Figure 2 Two special cases of traditional artificial potential field
1.2 改进人工势场
为了解决上述问题,定义目标点—实验车的连线与障碍物—实验车的连线之间夹角为θ0(可由车载毫米波雷达测得),在障碍物的异侧增设一个附加力Fadd,其与目标点—实验车的连线间的夹角为θ,实验车在任一点位的受力如图3所示。

图3 改进人工势场Figure 3 Improved artificial potential field
(1)目标不可达问题。障碍物斥力随S(M,Mobs)的减小而增大是实验车目标不可达的根本原因,由式(5)可知,实验车与障碍物的距离S(M,Mobs)越近,斥力越大,因此可以选用实验车到目标点之间距离S(M,Mg)作为距离调节因子对斥力计算式加以数值大小上的修正,改进后的斥力大小为
(8)
从式(8)可以看出,随实验车与障碍物间的距离的减小而斥力增大的趋势,因引入呈恒定减小的距离调节因子而得到抑制,可保证实验车所受的合力方向始终与前进目标方向大体一致,从而避免了局部路径规划中的目标不可达问题的出现。
(2)局部极小值问题。目标点引力与障碍物斥力的合力为0是局部极小值问题出现的关键。因此,为保证车辆不陷入局部路径规划中的极小值点,引入一个由θ角(限定θ>θ0)与S(M,Mg)共同控制的附加力Fadd(M):
Fadd(M)=k·S(M,Mg)cosθ。
(9)
式中:k为大于0的附加力增益系数,其取值大小对规划的局部路径长短有影响。
显然,由式(9)可见,即使实验车无限小距离接近目标点,以及雷达探测角θ0为0时,附加力也将始终不为0,故既可保证有效避开障碍物,又可在到达目标点处时衰减为0。
由此,实验车在改进人工势场中所受的合力可由式(7)改写为
(10)
2 算法设计与评价
2.1 算法设计
改进人工势场法算法流程如图4所示。当实验车接收到来自前方障碍物信息后,开始计算每个障碍物与车辆初始位置连线和X轴夹角;然后计算出各个分力并正交分解于X轴、Y轴;最后矢量相加求得合力。通过合力来确定实验车辆的下一位置,并时刻监控在规定时间内能否到达目标点并回到全局路径中:若到达,则局部路径规划成功;若不能到达目标点,则更新障碍物位置进一步规划。
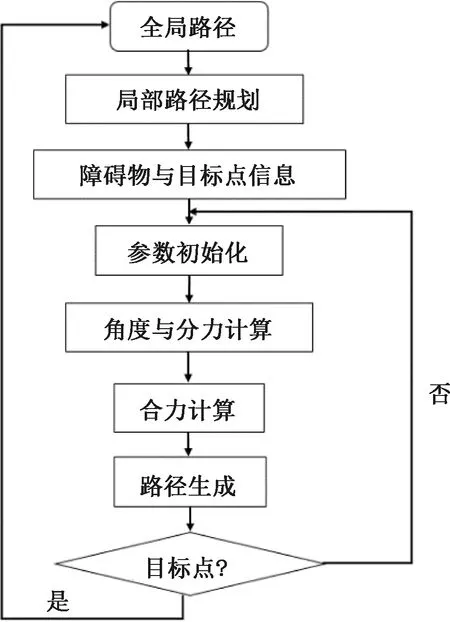
图4 改进人工势场算法流程Figure 4 Algorithm flow chart of improved artificial potential field
2.2 价值评价
为验证改进人工势场的优劣性,可从时效性TS与安全性QS两方面进行评价。
(1)时效性。设单位步长为Δd,实验车到目标点的局部路径规划长度为L,可算出总步数n(圆整),则时效性为
(11)
式中:Ti为单步计算时长。
时效性由单步计算时长与局部规划路径长度所决定,规划路径越短,单步时长越短,即时效性越好。
(2)安全性。设局部规划路径至障碍物最小碰撞安全距离为S,规划路径中出现极小值点的次数为K,安全性指标为
(12)
式中:h为安全系数,为大于或等于1的任意数。
对于某一局部规划路径,其安全性由极小值点出现的次数与最小碰撞安全距离决定,极小值点次数出现越少,则安全性越好。
3 仿真分析
3.1 附加力引入的影响
图5为用附加力增益系数表达的不同大小的附加力作用下的规划路径结果,表1为时效性和安全性评价结果。从图5可见,所有规划路径均能越过局部极小值点,但附加力的大小对最小碰撞安全距离大小的影响不同,从表1也可见引入附加力后的所有路径规划均未出现极小值问题。

图5 不同附加力增益系数下的路径Figure 5 Paths with different additional force gain coefficients
当附加力增益系数较小时(如k=1),规划路径几乎紧贴障碍物边缘而越过,其安全性指标过低,即碰撞安全距离过小,实际行车过程中仍存在避障失败的可能;当附加力增益系数过大时(如k=10),规划路径能可靠越过障碍物,但碰撞安全距离明显过大(安全性指标值最大),且规划路径步数较附加力增益系数为5时增加4.3%,时效性也增加了8.3%。
从图5(b)可见,当附加力增益系数取值分别为5、6和7时的3条规划路径基本上处于相互重合的状态,它们的碰撞安全距离和安全性指标也都十分接近,表明在该区间内规划路径具有较好的一致性,也说明采用附加力改进的人工势场规划算法具有较好的结果稳定性和可靠性。
3.2 距离调节因子引入的影响
图6(a)为改进人工势场下障碍物对实验车产生的斥力变化仿真曲线,Z轴表示无量纲斥力。图6(b)为将斥力峰值坐标投影在XOZ平面内的斥力峰值曲线图。
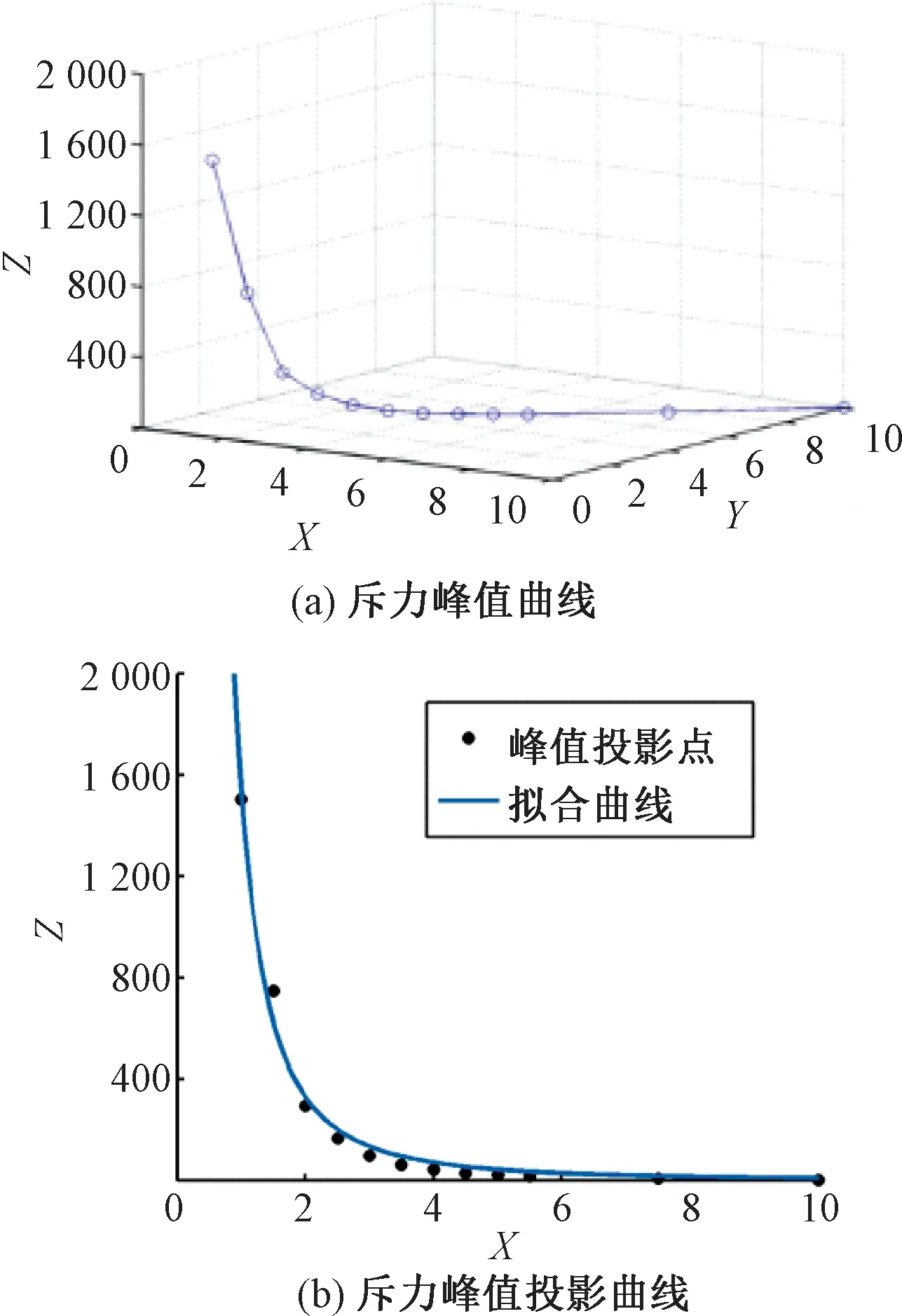
图6 改进人工势场斥力仿真曲线Figure 6 Repulsion change simulation curve of improved artificial potential field
定义实验车初始位置与目标点连线为中轴线,从图6可见,中轴线上不同位置障碍物产生的斥力峰值随其与实验车初始位置间的距离变化而变化:当障碍物距实验车较近时(如在实验车起始位置附近),斥力峰值很大;而当障碍物逐渐远离实验车时,斥力峰值则呈迅速下降的趋势,并在目标点附近所受斥力衰减为0,确保了实验车目标可达。
3.3 路径规划的价值评价
图7为引力增益系数为12,斥力增益系数为3,附加力增益系数为6,单位步长为0.2,障碍物数目为7,安全系数为1.5的仿真参数条件下,传统人工势场法与改进人工势场法的仿真规划路径算例。为保证传统人工势场可以获得完整路径,在出现局部极小值点时采用自动延续步长处理。
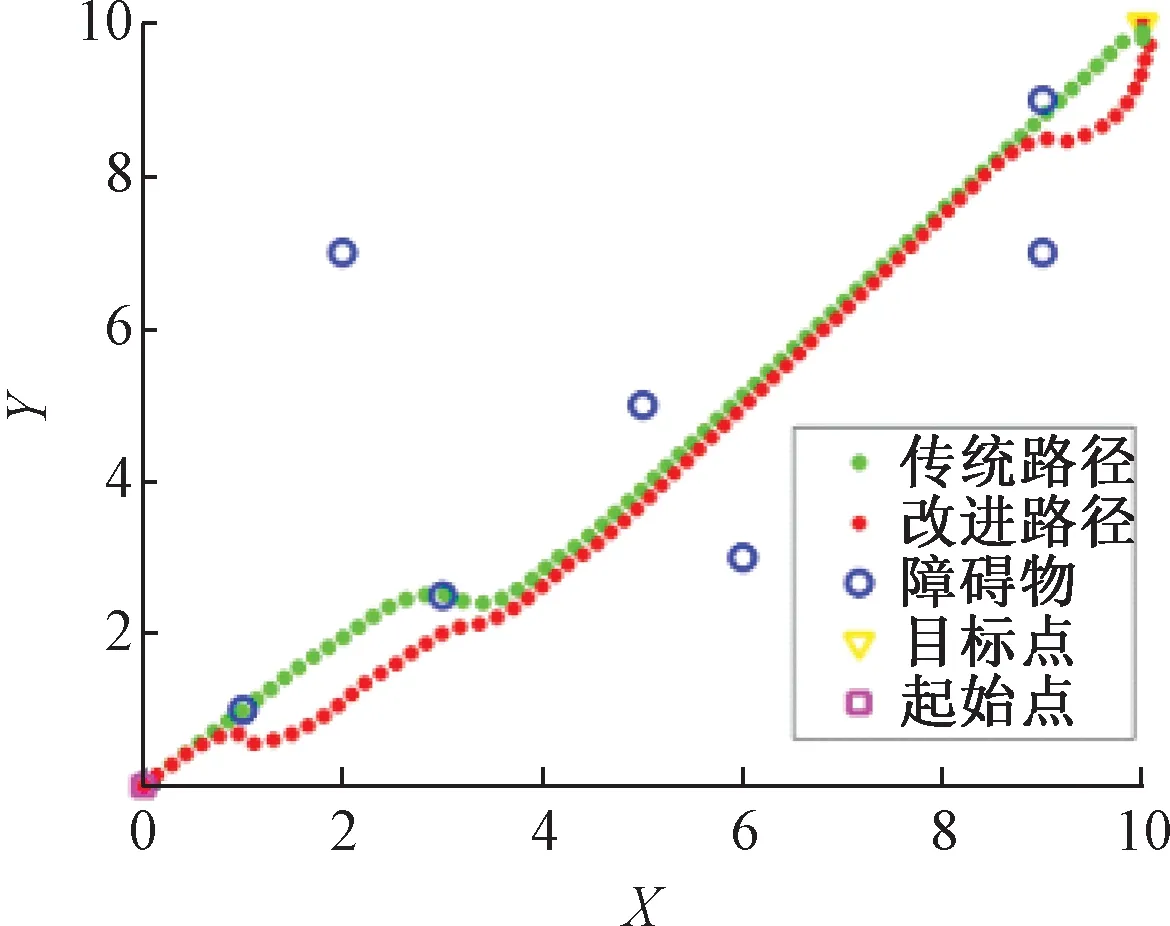
图7 局部路径规划Figure 7 Local path planning
从图7可见,传统人工势场规划算法在出现局部极小值点或障碍物距离目标点过近时,不能避障,并可能会出现局部震荡,而改进人工势场规划的路径,能成功越过障碍物,并可完全规避路径规划中极小值点的出现。
表2为传统及改进人工势场两种规划算法的价值评价结果。由表2可见,改进算法的单步计算时长略有增加,但由于所规划的路径不存在震荡区间,其计算时效性与传统人工算法的基本一致。同时,改进人工势场规划路径的最小碰撞安全距离远大于传统人工势场规划,因此其安全性得以大大提高。
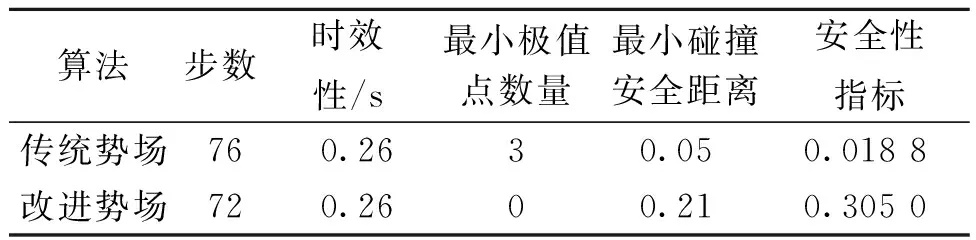
表2 时效性与安全性价值评价表Table 2 Valuation table of timeliness and security
4 结论
引入斥力调节因子和附加力对传统人工势场加以改进的局部路径规划算法,解决了存在的局部极小值和目标不可达两个问题。
(1)引入S(M,Mg)调节因子的改进人工势场规划算法可以显著降低斥力在目标点附近的影响,改进后的斥力峰值具有随障碍物与局部路径规划起始点的增加而呈现出指数级减小的规律,斥力在目标点附近衰减为0,确保实验车实现目标可达。
(2)引入k·S(M,Mg)增益量的附加力可改变局部极小值点处的合力大小与方向,能完全避免出现局部极小值点,使实验车按规划路径行驶越障过程中能与障碍物间保持合适的碰撞安全距离。
(3)采用距离调节因子与附加力耦合改进的人工势场算法的局部路径与传统路径时效性均为0.26 s,安全指标由传统人工势场法的0.018 8增大至0.305 0,可显著提高局部路径规划的安全性。

