人工智能中因果定义的探索

魏 涛，杜国平

(1.中国社会科学院大学 哲学院， 北京 102488； 2.中国社会科学院 哲学所， 北京 100732)

现阶段的人工智能是数学式的信息处理系统，在一定程度上可以回答问题、解决问题，但无法理解问题、思考问题，缺乏可解释性。而因果性解释能够回答为什么的问题，是科学解释的主要形式。朱迪亚·珀尔(Judea Pearl)将“为什么”作为科学解释的核心问题，认为当前的“智能机器缺乏对因果关系的理解，这也许是妨碍它们发展出相当于人类水平的智能的最大障碍”[1]。基于统计学的视角，珀尔等人构建了一套能够将预测、干预和反事实算法化的因果语言，通过因果模型表征因果知识，给出了因果关系的形式化、数学式的定义。HP定义是一种应用性定义，在一定程度上符合因果定义的基本要求：时序性、相关性和不间断性；可为人工智能领域表征因果知识提供方法，为确立实际原因提供一般性原则。

一、因果定义的划分

20世纪以来，对因果关系的讨论不再局限于哲学领域，还出现在统计学、心理学、物理学和人工智能等多个学科领域的研究中，由定性研究转向定量分析，由还原分析转向路径分析，呈现出学科结合的研究趋势。在哲学领域中，孔斯(Koons)认为：“近年来因果研究的分野主要来自对事件—类型间因果关系和事件—殊型间因果关系的关注。”[2]但是，从近几年的文献中可以发现，殊型和类型因果关系的研究并非是泾渭分明的，而是将反事实分析、语境、过程、时间等因素和概率因果论相结合，多元化地定义因果关系，并综合考察事件间因果关联的可能性。根据定义的不同出发点可将其分为3种：实质性定义、操作性定义和应用性定义。

(一)实质性定义

休谟(Hume)认为，人类能够经验到的是相似物象的恒常汇合，而无法感觉到物象之间的任何纽带，因此原因与结果之间不再具有必然性，而是一种或然性。物象出现时，会在心灵上产生一种习惯性的转移，这种转移实质上就是物象间的恒常汇合，也就是因果关系。由此，休谟给原因下定义为：“所谓原因就是被别物伴随着的一个物象，在这里我们可以说，凡和第一个物象相似的一切物象都必然被和第二个物象相似的物象所伴随。或者换一句话说，如果第一个物象不曾存在，那第二个物象也必不曾存在。”[3]休谟虽是在经验范围内追寻因果观念的本质，但是并未涉及具体事物的特征、时间、地点等信息，是在类型上定义因果关系，力图陈述的是“因果关系是什么”的问题，希望借助某种方式将物象间的接续关系还原到物象的性质、事态上。

在规则性定义中，休谟开创了反事实定义方法，还原因果关系的实质。而后的大卫·刘易斯(David Lewis)明确给出了因果的反事实定义。命题间的依赖关系包含了两个条件句：O(c)□→O(e)和﹁O(c)□→﹁O(e)，且命题间的反事实依赖关系可对应于事件间的反事实依赖关系。由此，事件e反事实地依赖于事件c，当且仅当两个反事实条件句O(c)□→O(e)和﹁O(c)□→﹁O(e)为真。命题间的真值关系映射到事件间为(1)若c发生，则e将发生；(2)若c不发生，则e将不发生。当e和c的反事实依赖关系成立时，则c是e的原因。同时，为坚持因果关系的传递性，将因果关系定义为殊型事件之间因果依赖的传递闭包：“令c、d、e……是殊型事件的有限序列，d依赖于c，c依赖于d，诸如此类等等，这个序列为因果链条。一事件是另一事件的原因，当且仅当存在这样一个连续的因果链条。”[4]因果链条的定义虽是为说明因果关系的传递性，但为因果关系的反事实依赖特征提供了有力辩护。

(二)操作性定义

20世纪以来，因果论发展的主要方向是运用统计学中的概率刻画原因和结果之间的关系，认为原因可改变结果发生的概率。概率的引入使得因果关系的探讨从经验范围缩小到科学实验中，通过观察、测量变量(可以是事件、数据、现象)之间的相关数据变化，运用数学公式计算变量间因果关系的随机性程度。概率计算的因果关系不再是一种“有或无”的关系，而是一种可能性分析。其中，概率因果论的代表性人物萨普斯(Patrick Suppes)追随休谟，将物象之间的伴随关系表示为一种概率关系，通过定义表面原因(prima cause)给出真实原因(direct cause)的定义，如下：

定义1：Bt′是At的表面原因，当且仅当

(i)t′﹤t； (t=时间)

(ii)P(Bt′)﹥0；

(iii)P(At/Bt)=P(At)。

定义5：事件Bt′是At的真实原因，当且仅当，Bt′是At的表面原因，且不存在t″和πt″，使得对于πt″的每个Ct″来说，

(i)t′﹤t″﹤t；

(ii)P(Bt′Ct″)﹥0;

(iii)P(At/Ct″Bt′)=P(At/Ct″)[5]。

萨普斯对真实原因的定义所要表达的意思为：若第一个事件的出现被第二个事件以较高的概率跟随，且无第三个事件存在于第一和第二事件之间，则第一个事件是第二个事件的原因。概率式的分析断言“X和Y是因果相关的”：在特定实例中，改变X的值将影响Y的值。这种改变往往发生在干预行为中，“相对于一个系统S，X引起Y当且仅当如果在系统S中发生了一个干预I，使得X的值发生了变化，相应的Y值也发生了变化，并且X与Y之间的这种关系是稳定的”[6]。对此，伍德沃德(James Woodward)从干预主义出发定义类型层面的因果关系：“X是Y的真实原因，当且仅当X对Y的影响不能被集合V中的任何其他变量所干涉，在下列意义上来说就是：当V中所有其他变量赋值与X变化无关的某固定数值时，存在对X的可能干涉将改变Y值或者Y的概率分布。”[6]

(三)应用性定义

哈尔彭(Joseph Y.Halpern)和珀尔将反事实依赖扩展为“据情形的依赖”(contingent dependency)给出了实际因果关系(殊型因果关系)的“初版定义”，之后为消除混杂因子，通过增强条件做出微调得到“最终定义”。“初版定义”(称为HP定义)如下：

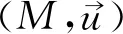
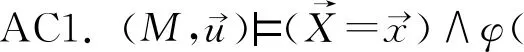
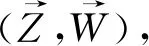
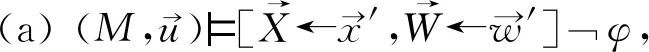
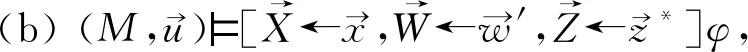
HP定义是方程结构模型式的定义，主要运用于经济学领域、社会科学领域和人工智能领域。结构方程模型建立在一般因果关系的知识基础上，对特定事件相关的知识背景进行编码，选定变量赋值，从而判定特定情形中具体事件的原因。结构方程模型也可称为因果模型，也是一种预测模型，通过变量赋值来预测行为的结果和干预的结果。干预变量取值可推翻原来的因果关系结构，即在不会干扰其他变量取值的情况下，破环某个变量的初始取值，计算结论变量取值，从而发现真实的因果关系。模型化或者形式化的定义是一种实践方法，基于知识和数据的组合阐明因果关系，进行因果推断，证明、分析因果假设，预测行为和政策的结果，评估、解释观察到的事件和情形。

二、因果定义合理性的判据

因果关系中的因和果可以是事物、现象、客体、情景等。从逻辑上来看，事物、现象、客体及情景都是关系者项，不同因果关系中涉及到不同的项，且可简单表示为cRe或者R(c，e)。从形式来看，两个变项c、e之间的因果关系是一种二元关系，基于实际中发生或者不发生取值0或1。c是e的原因当且仅当c=1和e=1，往往表示为c⟹e，即若c为真，则e存在原因，或者是c为e提供一种因果解释。概率的表示方法为P(E=1|C=1)>P(E=1|C=0)，意思为c出现时e出现的概率大于c不出现时e出现的概率。逻辑或者概率的表征方式取决于经验世界中的因果关系，所以判定变项之间是否具有因果关系，需要从内容方面做出考量。基于事实经验的要求，休谟认为符合通则的对象之间才有可能产生因果关联，由此奠定了因果关系成立的基调：原因先于结果，原因和结果之间在空间和时间上是相互接近的。而后，因果定义中引入概率、时间等因素，且与过程、语境相结合也未能改变休谟的基调。

(一)时序性

从逻辑上来看，时间是多维的，可划分为3种：先于关系、同时关系和后于关系，即A先于B、A和B同时、A后于B。因果关系涉及到时间问题，即原因和结果在时间上的先后问题。“时间本来是有方向的，这已往致将来只是根据于时间固有的方向而说的话，说因致果也是根据于时间底方向而说的话。”[8]时间的方向性导致因果的方向性，意味着因和果不是同时发生的，而是有先后顺序的，存在时间间隔。这种时间间隔的存在，不仅体现了因到果的一种变化，而且象征着因对果的作用需要经历一个过程。若因和果无时间上的间隔，二者处于同一时间，或者同时产生，就无法区分原因和结果，就无所谓经验上所认为的导致与被导致、引起与被引起的关系。因此，时间上的先后关系是定义因果关系的一种本质要求，确保了事件之间的关系是真实的，而非虚假的。因此，单纯从时间上来看，因果关系是因和果之间的一种连续或者接续关系，这种接续关系由时间的一维性所决定。

(二)相关性

因果关系者项是独立且相关的两个事件、现象等。从逻辑上来看，独立意味着二者之间是不相容的，而相关性却非逻辑上的相关，是经验或者事实的相关，这种相关是由事物的内在结构所决定的一种相关。第一，相关性是一种质上的关联，是事物性质间具有的某种联系。比如，在火柴可以点燃木柴的案例中，涉及到的变项有氧气、木材和火柴等，三者之间只有具备了一定的化学或者物理性质，在一定条件下才能够产生因果关系。第二，相关性还是一种时空的相关性，要求变项在时间和空间上的间隔是恰当的，作为原因的关系者项在时间t1上产生的作用经过恰当的时间和空间才能够形成结果，若空间距离过大、时间间隔过长，可能无法产生某种结果。比如，在球击碎玻璃的事件中，若踢球的力度较小，球飞行一定的距离落地，无法达到窗户也就不能导致玻璃破碎，球和玻璃之间不存在因果关系。所以，相关不一定是因果关系，但具有因果关系的事件之间必然具有相关性。

(三)不间断性

从原因到结果会经历一定的时间和空间这样一个过程。这个过程实质上是一个不间断的链条，且无居间事件的存在。若从初始事件到结果的链条中，存在居间事件，即c→c1→c2→…→e，居间事件也可能遮断初始事件到结果的关系。比如，登山者幸存的案例构造出的链条为：巨石滚落→巨石发出巨响→登山客惊觉→登山客躲避→登山客幸存，按照此链条得到不合常理的结论是巨石滚落使得登山客幸存。从经验上来看，巨石滚落导致的结果应为登山客受伤，而这种结果之所以没发生，则是“登山客躲避”而打破了原有的因果关系，而形成了新的因果关系，即登山客躲避导致登山客幸存。所以，从初始事件到结果的链条中，引发结果的不再是初始事件，而是距离结果最近的前置事件。正如因果模型中所示的，父变量是子变量的原因。在原因到结果的路径上，简单的图型表示变量间的因果关系，即C→E，表示从C到E存在一个直接的路径，C是E的原因。

三、HP因果定义的合理性及其困境

(一)HP终版定义

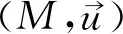
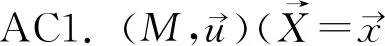
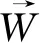
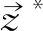
(二)合理性的分析

基于结构方程语言，珀尔等刻画因果关系成立的条件，结果并不总是反事实依赖于原因，而是在一定情形下依赖于原因，将传统的反事实依赖扩展到依情形而定的依赖，是一种依赖于语境的因果关系。非本质性的定义具有一定的合理性。

1．非时序因果关系中的时间信息

关于时序信息，在HP定义中似乎无法直观获取。变量间的因果影响是从非时序性的数据中获取的，即一种非时序性的因果关系。在此，基于统计学的观点，时间信息并不是区分因果关系的唯一标识。但是在定义过程中，对时间信息还是给予关注。比如，在定义潜在原因(potential cause)和真实原因(genuine cause)时，都包含有时间信息。变量X对Y有潜在因果影响，其中一个基本考量就是变量X早于且临近于Y才可能是Y的潜在原因或真实原因。结合时间信息可定义真实因果关系(genuine causation with temporal information)：即变量X对Y有因果影响，若第三个变量Z和语境S，同时先于X发生，使得1.(ZYS)；2.(ZY(S∪X)[10]。可解释为：“基于Z=Yt-2和S={Xt-3，Yt-3}，Xt-2作为Xt-1的潜在原因；基于Z=Yt-2和S={Yt-1}，Xt-1作为Xt的真实原因。”[10]关于这一点，珀尔通过图1给予说明，图1可解释为：在语境S中，若条件X可以将Z和Y之间的依赖关系转为独立关系，则X可调节Z和Y之间的依赖性；在Z先于X的情况下，这种调节蕴涵X对Y有因果影响。统计意义上谈论的时间可以和物理时间相一致或相反，或者对应于马尔可夫链中的任何方向。但是，在Z→X→Y链条中，作为一种由马尔可夫链所决定的统计时间只有一种，且与物理时间相一致。因此，统计现象必须展现出基本的时序偏差。虽然时间信息并不是因果关系的唯一标识，但是不包含时间信息的概率函数并不能单独推出模型中箭头的方向，而变量间不同的箭头方向有着不同的本质。所以，忽略时间信息所带来的结果是无法形成一种确定性的，正如珀尔提到的：“假设V=0(可观察变量)但缺乏时间信息，科学家无法排除基本结构是一种完备的、无环的和任意秩序的图型的可能性——一种结构可以模拟任何模型的行为，而不考虑变量排序。”[10]所以，HP定义虽关于时间信息的讨论并不直接，但是持一种认同态度。

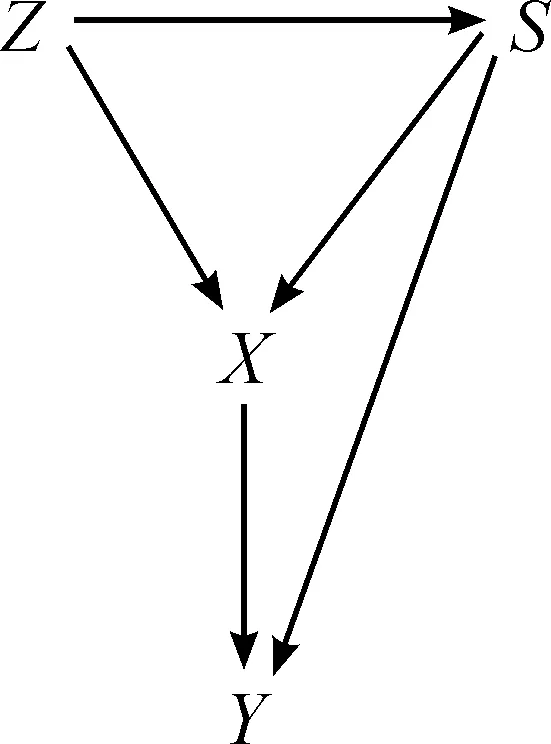
图1 包含时间信息的真实因果关系

2.模型中变量的相关性

HP定义中的因果关系者项为变量。在构建模型的过程中，首先面临的问题是如何选取变量的问题，而变量选取的基本依据是相关性。这种相关性展现在语境和模型中。在定义中，AC3作为最小条件发挥了“剃刀”作用，剔除不相关因素。比如，在查寻森林着火原因的过程中，变量包含F(森林着火)、L(雷击)和MD(纵火犯扔下点燃的火柴)等，而类似变量O(氧气充足)则作为隐形条件一般不出现在模型中，不作为原因的考虑因素。基于实际需要而选择的变量分为外生变量和内生变量。在理论上看来，内生变量集合V是未知的，可观察的变量可通过不同因果关系连结，由此适合已知概率分布的模型有多个甚至是不受限制的。若模型无所限制，就无法对基本现象的结构做出有意义的断言。因此，需要通过语境来约束变量的选择及其取值。作为已知项的外生变量，其取值是确定的，构成了特定的语境，而内生变量作为原因的候选者，其取值由外生变量通过方程决定。若变量X1…Xm是Y的真实原因，则Y通过方程可表示为：Y=FY(X1…Xm)，当对变量X1…Xm赋值时，将获得Y的取值，当X1…Xm的值变化时，Y的值将发生变化。所以，方程模型不仅刻画变量间的因果影响，还可以描述变量之间的依赖关系及反事实依赖关系，进而体现变量间的相关性。

3．因果图中的“父子关系”

HP定义建立在因果关系的表征基础上。其中，有向无环因果图(DAG)是表征因果关系的主要方式。有向无环图是一组有序对(V，E)，其中V表示图中结点的集合，E是连结结点的有向边集合。从结点X到结点Y的有向边表示X直接导致Y。X是Y的父结点，即X是Y的真实原因当且仅当从X到Y存在一条直接路径。如图2中，变量V={X，Y，Z，S，W}，在S→X→Y→W的链条中，S是父结点，X是子结点，从S引箭头到X表示S是X的直接原因，S的取值对X的取值有因果影响，且S通过其他变量不能产生对X的影响。同样，在此路径中，X结点阻断了Z到W的路径，即X遮断了S和X的子孙之间的联系，或者是结点S和X的子结点阻断了结点S和结点Y之间的信息流通，导致结点S和结点Y不可直接用箭头连接，S和Y、W是条件独立的，根据S的值并不能给Y、W提供其他的信息。这种条件独立体现在AC2条件中，在因果路径上，X是Y的原因，X的取值变化时，Y的取值也将发生变化，在变化过程中其他变量取值并不改变；当其他变量的取值变化时，X的取值不变，Y的取值也将不变。Y的取值是否变化与X的取值直接相关，即X和Y之间是一条无居间变量的因果链条。

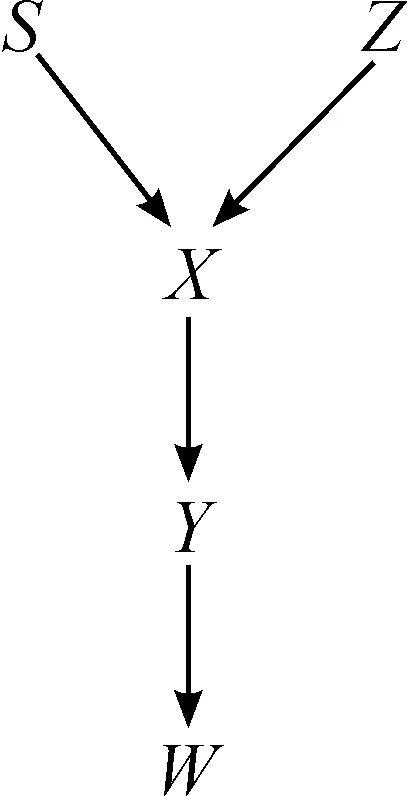
图2 因果链条中的“父子关系”

(三)HP定义的困境

“因果关系的HP定义是与模型相关的。在一种模型中，A可以是B的原因，但是在另一个模型中却不是。”[9]同一情形的因果模型可以是多个，模型不同，因果归因则不同。哪个模型更符合直观和实际，面临着模型选取的问题。造成结果差异的是变量的划分：即外生变量和内生变量的划分。“外生变量选择的不同将导致不同的结论，虽然看起来似乎准确地描述了相同的情形。”[9]从总体上来看，变量取值在一定程度上具有客观性，但是变量的划分带有一定的主观偏好。一个变量作为哪种性质变量出现，取决于建模者的需要，即所考虑的语境。比如，一起交通事故的原因，刹车故障、道路设置的不合理、不娴熟的驾车技术、酒驾、心理因素等都可能导致车祸。此时根据主体需要构建出的模型存在差别，车祸的归因则不同。若律师将醉酒和下雨作为外生变量的话，则刹车坏掉是车祸的原因，即U={D(醉酒)，R(下雨)}，U={B(刹车)，TA(车祸)}，若B=1，则TA=1。此模型中结构方程集合为：B=1;TA=1。若将下雨、醉酒这些因素划分内生变量中，则醉酒和下雨都是导致车祸的原因，即若D=1且R=1且B=1，则TA=1。形成的结构方程集合为：D=1;R=1;B=1;TA=1。模型无好与坏的区分，但责任划分却存在很大区别。对此，往往是通过增加一个或多个虚拟变量或者是工具变量来结构化情景而区分模型。比如，当D=0且R=0，B=1时即干预D和R的变量取值，而不改变关于B方程的取值，测量TA的取值。此构造的新模型的结构方程集合为：D=0，R=0，B=1，TA=？而TA的取值依赖统计数据，比如刹车的测量数据、驾驶者的心理因素等。变量间的因果影响的强度由数据决定，数据是否充分严重影响模型的稳定性。变量的选择问题转化了数据的充分性问题。此外，添加变量是否会模型变得杂乱或者无意义，也需要做出进一步的考量。

四、结语