基于改进人工鱼群算法的船舶进港排序

白响恩 李豹 徐笑锋

摘要：针对我国绝大部分港口遵循先来先服务（first-come-first-served， FCFS）调度方法引起的船舶进港总延误时间偏长的现象，提出一种基于改进人工鱼群算法（artificial fish swarm algorithm， AFSA）的船舶进港排序方法。改进算法的搜索精度更高和局部优化能力更强，利用这个改进算法得到的船舶进港排序使总延误时间更短。仿真结果显示，与FCFS调度方法和AFSA相比，改进算法的船舶进港总延迟时间分别减少了20.8%和5.2%。所提出的改进算法能为港口船舶进港排序提供有效支持。

关键词：  船舶进港排序; 先来先服务调度; 人工鱼群算法（AFSA）

中图分类号：  U692.4

文献标志码：  A

Sequencing of ships entering a port based on an improved

artificial fish swarm algorithm

BAI Xiangen， LI Bao， XU Xiaofeng

（a.Merchant Marine College; b.Engineering Research Center of Shipping Simulation，

Ministry of Education， Shanghai Maritime University， Shanghai 201306， China）

Abstract： In the most ports of China， the use of the first-come-first-served （FCFS）scheduling method makes the total delay time of ships entering a port

too long. To solve this problem， the sequencing method of ships entering a port based on an improved artificial fish swarm algorithm （AFSA） is proposed.By the improved AFSA with the higher search accuracy and the stronger ability of local optimization，the sequencing of ships entering a port with the shorter total delay time is obtained.The simulation results show that the total delay time of the improved AFSA decreases by 20.8% and 5.2% compared with FCFS scheduling method and AFSA， respectively.The improved AFSA can provide effective support for the sequencing of ships entering a port.

Key words： sequencing of ships entering port; first-come-first-served scheduling; artificial fish swarm algorithm （AFSA）

收稿日期： 2021-02-19

修回日期： 2021-04-16

基金項目： 国家自然科学基金（42176217）

作者简介：

白响恩（1984—），女，上海人，副教授，博士，研究方向为船舶交通管理，（E-mail）xebai@shmtu.edu.cn

0 引 言

随着全球一体化程度的加深以及航运业的发展，港口的货物吞吐量不断增长，船舶也向着大型化趋势发展。为保障船舶进港安全，我国计划开展一系列的港口扩建计划，但由于港口扩建周期较长，港口航道的通航能力无法在短期内得到提升。在现有基础上对船舶进港排序进行优化能在很大程度上缓解港口的压力。不同类型船舶在进港时间间隔上有所不同，对进港船舶排序进行优化，不仅能保障船舶进港的安全高效，而且可以增大航道的资源利用率，提高港口效益。

现阶段船舶进港排序主要采取先来先服务（first-come-first-served， FCFS）调度方法[1]，即根据船舶预计到达时间的先后决定船舶进港次序。该方法摒弃了船舶的有用信息，在船舶进港密集时段会使得船舶进港产生较长时间的延误。船舶进港排序问题属于典型的组合优化问题[2]，目前针对船舶进港总延误时间较长的现象，国内外学者进行了大量的船舶进港排序问题的研究。解决船舶进港排序的算法包含两大类。一类是经典的排序方法，包括模糊综合评定法[3]、排队论[4]等方法，模糊综合评定法和排队论在解决排序问题时具有信息丰富、排序结果贴近实际结果的特点。然而，在某些港口在特定时间内进港船舶数量较多的情况下，这两种算法的计算复杂、耗时增加的缺点尤为明显。另一类是智能仿生学算法，如基于蛙跳算法的排序法[5]、基于人工鱼群的排序方法等。HANSEN等[6]通过研究不同类型船舶之间的相互影响，构建了连续和离散泊位分配数学模型，实现船舶队列整体延误时间最短。童珊[7]研究了不同类型船舶的优先级，通过给船舶类型和预计进港时间等因素分配权重，构建船舶完工时间或等待时间之和最小的进港模型，但两者均未考虑船舶进港时间间隔因素，在船舶进港安全性上略有不足。叶子奇[8]构建了京唐港船舶调度混合整数线性模型，提出一种启发式算法——模拟退火算法，实现船舶进出港总延误时间最短;该算法局部寻优能力强，但是在全局寻优方面的性能比智能仿生学算法的低。孙绍文等[9]和郑红星等[10]通过调整船舶的靠泊顺序，规避潮汐因素的影响，保证船舶在港时间最短，但没有考虑船舶进港过程中的延误时间长短。

本文提出一种基于改进人工鱼群算法（artificial fish swarm algorithm，AFSA）的船舶进港排序算法，通过模拟鱼群的行为来确定较优的进港队列。AFSA属于智能仿生学算法，因为引入了种群的随机初始化机制，所以该算法比其他算法对初始参数的依赖低。船舶进港排序问题需要的初始信息较少，更贴合智能仿生学算法的思想。在解决船舶进港排序问题中，改进的AFSA既能保持算法全局收敛快的特性又具备启发式算法局部寻优强的特点;引入的自适应参数既能体现前期行为选择在精度方面的优势，又能加强后期算法跳出局部极值的能力，从而在一定程度上减少船舶进港总延误时间。

1 问题描述

1.1 背景概况

进港船舶调度问题是港口交通规划管理中的重要问题之一，具有多个约束，比较复杂。

FCFS调度方法具有简单、易用且公平的特点，但是摒弃了很多外在的有用信息和便利条件，调度效率低下、灵活性差，船舶进港的总延误时间较长，给港口带来额外的开销。进港船舶调度优化需要解决的实际问题是如何对进港船舶进行排序，减少船舶进港总延误时间。鱼群算法作为一种寻优算法能通过对鱼群行为的模拟，以船舶进港总延误时间最短为目标函数，寻找全局最优进港船舶序列。

1.2 问题描述

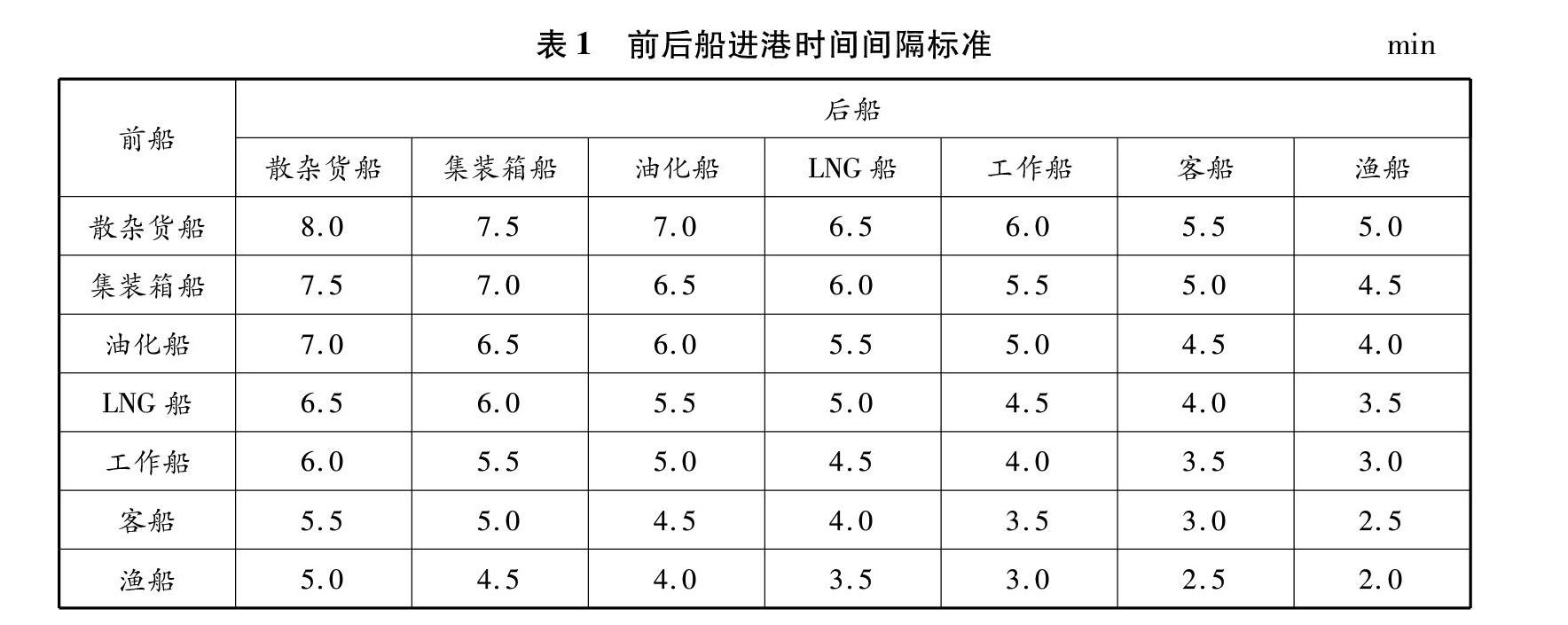
某港口在某段时间内将有一批船舶到达，根据这批船舶预计到达时间确定一个初始船舶进港序列{Ai}，i代表船舶进港序号，i∈{1，2，…，n}。现要对不同类型船舶在允许的安全间隔距离下，重新规划船舶进港次序，使船舶进港总延误时间最短。Te表示船舶预计进港时间，Ts表示船舶实际进港时间。根据船舶类型的不同，连续两艘船进港时间间隔也有相应的规定。船舶进港时间间隔指前后两艘船进港时的最短安全间隔时间，一般指进港时前后两艘船的间隔距离与行驶速度的比值。本文船舶数据来源于宁波舟山港引航站的统计，船舶类型主要包括散杂货船、集装箱船、渔船等7种。宁波舟山港的渔船一般不适用主航道，本文选择增添渔船这种船型，以验证多船型、不同进港时间间隔情况下船舶排序算法的性能。实际港口操作不局限于这7种船舶类型，港口可根据实际情况自行增减。考虑多船型的前后船进港时间间隔标准见表1。

用Te，i表示第i艘船的预计进港时间;Ts，i和Ts，i-1分别表示第i艘船和第i-1艘船的实际进港时间，ΔTi-1，i表示第i艘船与第i-1艘船的实际进港时间间隔，则

Ts，i=max {Te，i，Ts，i-1+ΔTi-1，i}（1）

第i艘船的延误时间Tf，i为

Tf，i=Ts，i-Te，i（2）

根据以上描述，得出单航道条件下，n艘船进港总延误时间最少的目标函数为

F=minni=1Tf，i（3）

2 AFSA的基本原理

2.1 AFSA的基本思想

AFSA[11]是一种智能仿生学算法，研究者通过研究一片水域中鱼群行动轨迹与区域食物浓度的关系，发现鱼群会通过主动觅食和群聚等行为向当前水域中食物浓度最高的區域聚集。AFSA是对鱼群的行为进行模拟并归纳总结出的一种优化方法。

在外界环境因素与人工鱼个体的相互影响下，各条人工鱼

做出最优行为选择，将每条人工鱼的状态信息记录在“公告板”上，达到终止条件后输出“公告板”上的信息即最全局最优解。“公告板”是算法的一个存储变量，用于记录人工鱼的最优状态，每次人工鱼的行为选择结束后，检查自身状态信息，若优于公告板的状态，则更新状态信息。

2.2 AFSA的行为描述

在解决船舶进港排序问题的过程中，AFSA将鱼群的行为分为4种，并定义了相关参数。

Si表示人工鱼的当前状态，代表一种船舶进港排序方案;Yi为当前状态下的目标函数，表示当前状态下

的食物浓度，即当前方案下的船舶进港总延误时间;Xv表示人工鱼视野范围的半径;

Xs表示人工鱼移动的步长;n表示觅食过程中人工鱼的最大尝试次数;δ为拥挤度因子。

（1）觅食行为：鱼群会根据视野范围内食物浓度的大小，选择游动的方向。人工鱼当前状态为Si，在以Xv为半径的人工鱼视野范围内选择一个新状态Sj，比较两个状态下目标函数的大小。若Yi

（2）聚群行为：人工鱼个体会趋向人工鱼数量较多的区域前进。人工鱼当前状态为Si，其视野范围的中心位置xc处伙伴的状态为Sc，视野范围内的伙伴数为m，水域内人工鱼总数为N。若m/N<δ，则说明xc处食物浓度高，拥挤度低;如果Yc

（3）追尾行为：人工鱼发现伙伴位置附近食物浓度较大会尾随最优人工鱼向其方向前进。人工鱼当前状态为Si，其视野范围内状态最优的伙伴的状态为Sb，如果满足Yi

（4）随机行为：人工鱼在不执行上述3种行为的条件下，会在视野范围内向任意方向前进，此过程会不断持续直至满足上述条件跳出随机行为。随机行为也是一种无目的的觅食行为。

3 AFSA的改进

AFSA作为一种随机搜索算法，具有对初值要求不高、全局收敛性能好的特点，能够比FCFS调度方法更好地解决船舶进港排序问题，有效减少船舶

进港总延误时间。然而，该算法在搜索过程中受鱼群固定视野和步长参数的影响，搜索区域大小和收敛速度受到限制，容易导致鱼群在邻近范围内进行盲目搜索，陷入局部寻优。

针对上述的问题，对AFSA进行改进，引入自适应参数[12]，使其视野范围和移动距离随周围环境信息的变化而变化，提高搜索效率。结合局部搜索优化算法[13]的优点，通过细致地划分邻域，精确确定局部最优值。

3.1 自适应视野

自适应参数的设计思想是：最优人工鱼一般位于极值点周围，在离极值点越远的区域，鱼群搜索时要求的视野范围和步长应越大，这样才能更快地向最优人工鱼移动;在离极值点较近的区域，视野范围和步长设计应偏小，以提高搜索精度。迭代过程即为人工鱼群不断向最优人工鱼聚集的过程，

在该迭代过程中鱼群的视野范围逐步减小，搜索效率提升，发现全局极值点更快。

鱼群在搜寻食物的前期，对视野范围内的人工鱼进行随机选择。视野的随机性也导致移动步长具有不确定性，故前期搜索容易陷入盲目搜索。

自适应视野和步长的提出，能使鱼群在搜索过程中根据外界环境信息动态地调整视野和步长的大小。

引入衰减因子α，α∈[0，1]。人工鱼自适应视野变化过程可描述为

Xv，k+1=αXv，k（4）

在觅食行为中，Xv在迭代时会不断变化直至为定值，使寻优过程趋向稳定。

3.2 自适应步长

步长参数影响人工鱼在执行聚群和追尾行为时移动速度的大小，人工鱼在视野范围内发现最优人工鱼时会通过聚群或追尾行为向其移动，因此步长会根据视野的变化进行调节。人工鱼自适应步长的确定是一种基于视野的改进方案[14-15]，在视野变动的基础上引入视步系数β，β∈[0，1]。根据“公告板”中的食物浓度和最优人工鱼的位置信息，通过视野值和视步系数计算人工鱼在聚群和追尾行为中的最大步长。

Xs=βXv（5）

引入自适应步长可以使寻优收敛加快，使大幅震荡现象减少。

3.3 局部搜索算法

局部搜索算法是一种贪心搜索算法，算法每次从当前邻域内选择一个最优解作为当前解，直到达到一个局部最优解。局部搜索算法的限制在于只能在一个指定的局部区域内找到最优解。爬山算法是局部搜索算法的一种，算法在执行过程中首先会选取一个节点，然后与其周围的邻居节点比较节点值的大小，得到邻域内最大值，即山峰的峰顶。得到的解是否是全局最优解常取决于初始节点的位置，若初始节点的位置在全局最优解附近，则更容易得到全局最优解。

传统AFSA易于跳出局部最优，迭代时能较为精确地选取最优人工鱼的位置，引入爬山算法可以划分多个邻域，

能在初步得到的最优人工鱼的位置附近通过不断比较，确定新的最优人工鱼，进而得到全局最优解。

3.4 改进AFSA的流程

综合爬山算法局部寻优能力强和AFSA全局收敛性能高的特点，并引入自适应视野和步长参数，提高算法的速度和精度。改进后的AFSA执行过程如下：

（1）初始化人工鱼数量为100条（每条鱼的位置随机），并设置其他参数的值。读入船舶信息，待排序船舶的数量即为鱼群搜索位置信息的数量，信息在水域中的位置随机分布。假设有10艘船等待排序，则鱼群搜索位置信息的数量为10。

（2）开始第一次迭代，每条人工鱼结合自身位置和目标位置信息反馈，通过不同行为选择遍历10个位置信息，遍历10个位置信息的先后顺序代表10艘船的一种排序方式，序列的目标函数即船舶进港总延误时间。

（3）对于遍历完的10个位置信息，人工鱼采用爬山算法划分邻域。划分邻域的方法是：在搜索得到的位置信息中随机选取两条互换位置，产生一个新的排序方案，然后比较划分前后船舶队列的目标函数值，并将得到的最优人工鱼状态信息赋值给“公告板”。

（4）重复上述操作，算法在达到最大迭代次数时终止，输出全局最优解。

改进后的算法先通过自适应参数加快行为的选择和执行，快速得到整个水域食物浓度较高的一个解域，再以爬山算法在邻域中进行快速局部搜索获得精确解，最终提高算法的收敛速度和精度。

4 应用案例分析

宁波舟山港是我国重要的港口之一，也是我国水上运输较为繁忙、船舶进港密度较大的港口之一。宁波舟山港包括了虾峙门和条帚门两条航道，其中虾峙门航道承载了港口九成以上船舶的进港负荷。为验证改进的AFSA能有效减少船舶进港总延误时间，选取2018年2月1日至2月7日9：00—12：00宁波舟山港虾峙门航道的进港船舶数据，采用FCFS调度方法、传统AFSA和改进AFSA进行仿真模拟，比较3种调度方法得到的船舶进港总延误时间。

假设航道环境条件正常（没有大风、大雾、涨潮等特殊现象），船舶航速为进港安全速度，船舶进港时间间隔满足表1所示的标准，且无船舶追越行为。由图1可知，改进后算法能更快地追寻到最优人工鱼的位置，并且在邻域内的寻优较为平稳，能很快得到全局最优值。

对2018年2月1日9：00—12：00船舶进港数据采用3种算法分别进行处理，仿真结果见表2。由仿真结果可知，采用FCFS调度方法、传统AFSA和改进AFSA对进港船舶进行排序，最终船舶进港总延误时间分别为141.63 min、112.87 min和108.35 min。计算可得，采用改进AFSA得到的船舶进港总延误时间较采用FCFS调度方法和传统AFSA得到的分别减少23.5%和4.0%。改进AFSA能减少船舶进港延误，提高船舶进港效率。

3种排序方法的仿真结果见表3。由表3中的数据计算可知，改进AFSA与FCFS调度方法和传统AFSA相比，船舶进港总延误时间平均减少了33.28 min（20.8%）和3.35 min（5.2%）。数据结果表明改進AFSA在解决船舶进港排序问题上表现更为优秀。

5 结束语

针对港口采取的先来先服务（FCFS）调度方法会造成船舶进港总延误时间较长的问题，提出一种基于改进人工鱼群算法（AFSA）的船舶进港排序方法。仿真结果显示，采用改进AFSA比采用当前港口执行的船舶FCFS调度方法能够减少20%左右的船舶进港延迟时间，比采用传统AFSA减少5%左右的船舶进港延迟时间。仿真结果验证了改进AFSA求解船舶进港排序问题的可行性和有效性。本文在解决船舶进港排序问题中，未考虑外在因素对船舶进港排序的影响，因此，如何对算法添加约束条件和解决外在因素的影响，是今后进一步研究的方向。

参考文献：

[1]BRANDWAJN A， BEGIN T. First-come-first-served queues with multiple servers and customer classes[J]. Performance Evaluation， 2019， 130： 51-63. DOI： 10.1016/j.peva.2018.11.001.

[2]赵晓智. 组合优化问题的尺度邻近点算法研究[D]. 天津： 中国民航大学， 2020.

[3]孟健. 黄骅港20万吨级散杂货船重载乘潮进港通航风险评估[D]. 大连： 大连海事大学， 2017.

[4]赵百岗. 基于排队论的航道通过能力及饱和度研究[D]. 大连： 大连海事大学， 2013.

[5]徐肖豪， 吴青， 黄宝军. 多跑道航班排序的改進蛙跳算法研究[J]. 航空科学技术， 2014， 25（2）： 6-11.

[6]HANSEN P， OGˇUZ C，

MLADENOVIC' N. Variable neighborhood search for minimum cost berth allocation[J]. European Journal of Operational Research， 2006， 191： 636-649. DOI： 10.1016/j.ejor.2006.12.057.

[7]童珊. 基于船舶优先权的集装箱港口泊位分配问题[J]. 交通运输工程与信息学报， 2012， 10（1）： 105-110.

[8]叶子奇. 基于混合遗传模拟退火算法的京唐港船舶调度优化[D]. 武汉： 武汉理工大学， 2019.

[9]孙少文， 杨斌， 胡志华. 潮汐影响下的港口离散泊位分配问题研究[J]. 合肥工业大学学报（自然科学版）， 2014， 37（4）：

486-492. DOI： 10.3969/j.issn.1003-5060.2014.04.023.

[10]郑红星， 吴云强， 邵思杨， 等. 考虑潮汐影响的泊位分配与船舶调度集成优化[J]. 信息与控制， 2020， 49（1）： 95-103， 113. DOI： 10.13976/j.cnki.xk.2020.9091.

[11]杨鹏. 人工鱼群算法的应用研究[D]. 兰州： 西北师范大学， 2017.

[12]谭璟， 张永祥， 张大胜， 等. 基于自适应人工鱼群算法的含水层参数确定[J]. 人民长江， 2018， 49（增刊1）： 71-74， 80. DOI： 10.16232/j.cnki.1001-4179.2018.S1.017.

[13]LIU Zhifeng， QIAO Peng， YANG Wentong， et al. Local search optimization immune algorithm based on job insert method for HFSS[J]. Advanced Materials Research， 2011， 267： 947-952. DOI： 10.4028/www.scientific.net/AMR.267.947.

[14]邱诗怡. 基于改进人工鱼群算法的智能机器人路径规划研究[D]. 武汉： 湖北工业大学， 2019.

[15]姚正华. 改进人工鱼群智能优化算法及其应用研究[D]. 徐州： 中国矿业大学， 2016.

（编辑 贾裙平）