水铁联运专线建设投资演化博弈分析

盛进路 李小凤 于敏 龚毅 杨忠振

摘要：针对谁来主导投资建设水铁联运专线问题，通过分析其中涉及的主要利益者之间的利益关系，建立三方演化博弈模型。通过演化博弈理论并结合MATLAB仿真，揭示在有限理性条件下，博弈各方进行决策的行为特征及其稳定状态。结果表明：在投资收益大于原有收益情形下，政府和港口部门将选择独立投资或合作投资建设水铁联运专线，铁路部门将选择合作投资建设水铁联运专线。

关键词：  综合交通运输; 交通運输经济; 投资策略; 水铁联运; 演化博弈

中图分类号：  F512.3

文献标志码：  A

收稿日期： 2021-03-25

修回日期： 2021-06-30

基金项目： 铁路与海运协同的外贸集装箱运输系统优化研究（72072097）

作者简介：

盛进路（1976—），男，山东烟台人，教授，博士，研究方向为港航企业运行与管理，（E-mail）forwardlulu@163.com

Meeting of the Waterborne Transport Division， World Transport Convention 2021 （WTC 2021）

Analysis on investment evolutionary game of water-rail combined transport dedicated line construction

SHENG Jinlu1，2， LI Xiaofeng1， YU Min1， GONG Yi1， YANG Zhongzhen3

（1. College of Traffic & Transportation， Chongqing Jiaotong University， Chongqing 400074， China;

2. Chongqing Key Laboratory of Transportation Engineering， Chongqing 400074， China;

3. Faculty of Maritime and Transportation， Ningbo University， Ningbo 315211， Zhejiang， China）

Abstract： Aiming at the question of who will lead the investment in the construction of the water-rail combined transport dedicated line， a tripartite evolutionary game model is established by analyzing the interest relationships among the main stakeholders involved. Through the evolutionary game theory combined with MATLAB simulation， it reveals the behavioral characteristics and stable states of decision-making of all parties in the game under bounded rationality conditions. The results show that： when the investment profit is greater than the original profit， the government and the port department will choose to invest independently or cooperatively in the construction of the water-rail combined transport dedicated line， and the railway department will choose to invest cooperatively in the construction of the water-rail combined transport dedicated line.

Key words： integrated transportation; transportation economy; investment strategy; water-rail combined transport; evolutionary game

0 引 言

水铁联运指铁路直达港口，中间不需要借助第三方运输的方式，水铁联运既能提高运输效率，降低物流成本，又能发挥“大批量、低污染”的绿色优势，是现代交通运输发展的必由之路。然而，目前我国水铁联运发展与发达国家相比仍较落后。近年来，国家出台了系列宏观政策以推动水铁联运发展，其中《交通强国建设纲要》提出要构建安全、便捷、高效、绿色、经济的现代化综合交通运输体系，强化铁路运输网络，并对加强港口与铁路衔接，解决铁路进港“最后一公里”问题提出了明确要求。因此，加强水陆口岸功能衔接，实现货物运输无缝衔接，能更好地发挥铁路、水路运输对国民经济和对外贸易的支撑保障作用。本文从利益关系和投资策略两方面探讨水铁联运专线建设投资问题。

近年来，国内外学者关于水铁联运的研究主要侧重于水铁联运的发展、水铁联运体系构建、水铁联运场站布局规划等。赵严等[1]从水铁联运外部经济环境的角度，提出我国水铁联运的“一港一线多城市”和“一港多区域”两种发展模式;张国伍[2]结合“一带一路”发展倡议探讨了我国多式联运存在的优势和劣势，并从体制机制、基础设施、宏观政策等层面提出多式联运发展建议;文献[3-5]从理论上研究水铁联运问题，分析影响我国水铁联运发展的重要影响因素;叶泫蠲[6]通过分析广西北部湾港区实施水铁联运的优势，提出完善该港区水铁联运发展的战略措施;黄起龙等[7]通过构建水铁联运港政府服务系统动力学模型，得出地方交通运输主管部门对水铁联运港政府服务效率具有较大影响，交通运输部和地方人民政府的影响较小且影响方式存在区别;郭静妮等[8]从设施布局、作业组织模式和组织衔接模式三方面，优化了水铁联运子体系布局及模式，并提出了基于集装箱运输的水铁联运全方位方案体系;邹涛[9]从运输组织、土地使用和项目实施三方面研究了铁路港口站的规划与设计;YANG等[10]提出了一种综合考虑进出口水铁联运集装箱装卸作业时间和能耗的双目标优化模型，以改善水铁联运集装箱码头的运营服务。

上述研究主要关注水铁联运的发展趋势和发展体系，对实现水铁联运无缝衔接的研究却较少涉及。实现水铁联运无缝衔接是水铁联运发展的前提，对促进我国物流企业降本增效具有深远意义。因此，本文在前人理论研究的基础上，分析水铁联运专线建设投资中涉及的政府、港口部门和铁路部门等主要利益者之间的利益关系，建立政府、港口部门和铁路部门三方演化博弈模型，利用MATLAB寻求均衡解，以期找到加快水铁联运专线建设的方案，促进水铁联运快速发展。

1 水铁联运专线建设投资中主要利益者关系分析

我国水铁联运实现无缝衔接仍面临着许多实际问题，最主要的问题是只有少数港口建设了水铁联运专线。由于水铁联运专线投资建设中涉及多种类型的利益相关者，而各个利益主体都不愿意主动投资建设水铁联运专线，所以水铁联运无法做到有效衔接。因此，通过分析各个利益者之间利益关系，探索优化现有规制策略的有效途径来协调利益相关者之间的利益冲突，以加快水铁联运专线建设，实现水铁联运无缝衔接。

1.1 利益主体

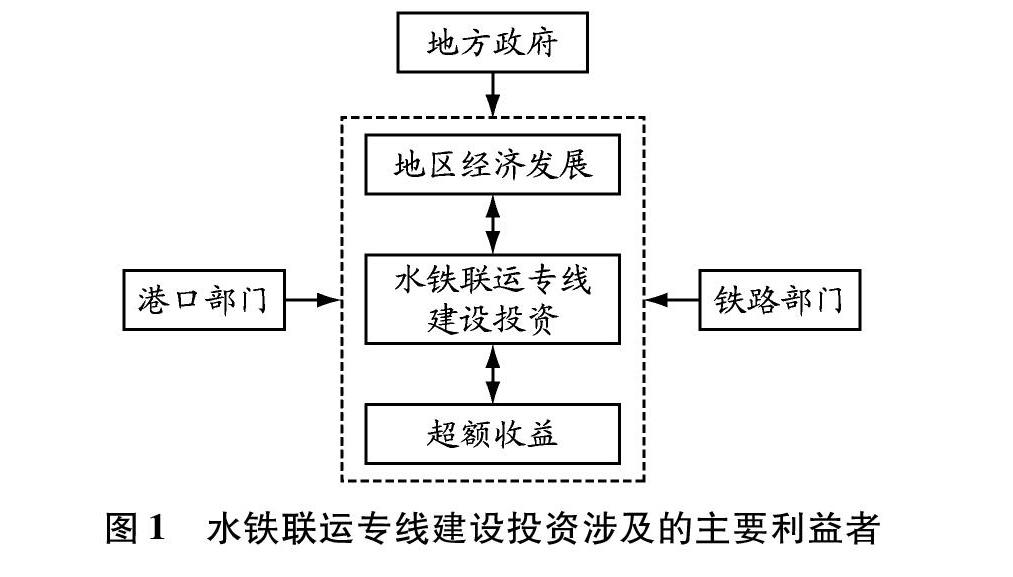
水铁联运专线建设投资涉及的主要利益者包括地方政府、港口部门和铁路部门。地方政府为了加快当地经济发展，有投资建设水铁联运专线的意愿;港口部门作为实现水铁联运无缝衔接后的直接受益者，希望水铁联运专线能够早日建成;水铁联运专线建成后将会增加铁路部门的货源量和货物种类，因此铁路部门从获益角度也有意愿投资水铁联运专线建设。这些利益相关者的决策行为共同影响水铁联运专线的投资建设（见图1）。

1.2 利益關系

若港口部门投资水铁联运专线建设，则其建成后将会提高港口的货源量，在给港口带来较大收益的同时也能提升当地经济水平，给政府带来一定的收益;同理，若铁路部门投资水铁联运专线建设，则其建成后将提高铁路集疏运能力，降低物流成本，在带来较大收益的同时也能提升当地经济水平，使政府获得额外收益;若政府投资水铁联运专线建设，则其建成后将会给港口部门和铁路部门带来超额收益，同时政府获得更多的税收。因此，政府、港口部门和铁路部门作为水铁联运专线建成后的受益方，其利益关系相互影响、相互促进。

2 模型构建

2.1 问题假设

假设1：假设水铁联运专线建成需要的投资成本为C，建成后带来的额外收入为ΔE。

假设2：假设政府（G）有两种策略可选择：投资建设水铁联运专线（Gj）和不投资建设水铁联运专线

（Gi）。当政府选择策略Gj时，其付出的投资成本为αC，获得的额外收入为αΔE，其中α指政府在水铁联运专线建设项目上的投资、收入分配比例;当政府选择策略Gi时，依托原有的运作模式也能获得收益，此时成本为C1，收入为E1。

假设3：假设港口部门（P）有两种策略可选择：投资建设水铁联运专线（Pj）和不投资建设水铁联运专线（Pi）。当港口部门选择策略Pj时，其付出的投资成本为βC，获得的额外收入为βΔE，其中β为港口部门在水铁联运专线建设项目上的投资、收入分配比例;当港口部门选择策略Pi时，依托现有业务也能获得收益，此时成本为C2，收入为E2。

假设4：假设铁路部门（R）有两种策略可选择：投资建设水铁联运专线（Rj）和不投资建设水铁联运专线（Ri）。当铁路部门选择策略Rj时，其付出的投资成本为θC，获得的额外收入为θΔE，其中θ为铁路部门在水铁联运专线建设项目上的投资、收入分配比例;当铁路部门选择策略Ri时，依托现有业务也能获得收益，此时成本为C3，收入为E3。

假设5：当政府、港口部门和铁路部门中的两方及以上选择投资建设水铁联运专线时，将出现合作投资，满足α+β+θ=1，其中0≤α≤1，0≤β≤1，0≤θ≤1。

假设6：本文考虑水铁联运专线建成后所带来的收益是一个长远收益，即ΔE-C>Em-Cm，其中m=1， 2， 3。为计算简便，令E^=ΔE-C，E^1=E1-C1，E^2=E2-C2，E^3=E3-C3。

2.2 演化博弈模型构建

假设在博弈开始阶段：政府选择策略Gj的概率为x，选择策略Gi的概率为1-x;港口部门选择策略Pj概率为y，选择策略Pi的概率为1-y;铁路部门选择策略Rj的概率为z，选择策略Ri的概率为1-z。由演化博弈性质可知，在博弈过程中，每个参与者选择某个策略的概率是不断变化的，因此在博弈的每个周期，政府、港口部门和铁路部门选择“投资建设水铁联运专线”策略的概率是在不断变化的，其支付矩阵见表1。

2.2.1 政府决策策略稳定性分析

根据支付矩阵，可以得出政府选择策略Gj或Gi的期望收益为

Ex（Gj）=（y（1-z）（α-1）+zα-z+1）E^

（1）

E1-x（Gi）=E1-C1

（2）

则政府选择策略Gj的复制动态方程为

F（x）=dxdt=x（1-x）（（y（1-z）（α-1）+

zα-z+1）E^-E^1）

（3）

令A=E^1-E^+zE^（1-α）E^（α+z-αz-1），由复制动态方程稳定性可知：（1）当y=A时，F（x）≡0，即x取任意值时，方程都处于稳定状态，代表此时政府可以选择策略Gj，也可以选择策略Gi。（2）当y≠A，F（x）=0时，分两种情况进行讨论。①当00，此时x=0为稳定策略，即当港口部门选择策略Pj的概率小于A时，政府将选择策略Gi。②当A0，F′（1）<0，此时x=1为稳定策略，即当港口部门选择策略Pj的概率大于A时，政府将选择策略Gj。政府的决策演化动态图如图2所示。

2.2.2 港口部门决策策略稳定性分析

同理，港口部门选择策略Pj或Pi的期望收益为

Ey（Pj）=（z（β-1）（1-x）+

x（β-1）+1）E^

（4）

E1-y（Pi）=E2-C2

（5）

则港口部门选择策略Pj的复制动态方程为

F（y）=dydt=y（1-y）（（（β-1）（z（1-x）+

x）+1）E^-E^2）

（6）

令B=E^2-E^+xE^（1-β）E^（β+x-βx-1），由复制动态方程稳定性可知：（1）当z=B时，F（y）≡0，此时y取任意值，方程都处于稳定状态，港口部门既可以选择策略Pj，也可以选择策略Pi。（2）当z≠B时，F（y）=0，分两种情况进行讨论。①当00，此时y=0为稳定状态，即当铁路部门选择策略Rj的概率小于B时，港口部门将选择策略Pi。②当B0，F′（1）<0，此时y=1为稳定状态，即当铁路部门选择策略Rj的概率大于B时，港口部门将选择策略Pj。港口部门的决策演化动态图如图3所示。

2.2.3 铁路部门决策策略稳定分析

铁路部门选择策略Rj或Ri的期望收益为

Ez（Rj）=（x（1-y）（θ-1）-yθ-y+1）E^

（7）

E1-z（Ri）=E3-C3

（8）

则铁路部门选择策略Rj的复制动态方程为

F（z）=dzdt=z（1-z）（（x（1-y）（θ-1）-

yθ-y+1）E^-E^3）

（9）

令C=E^3-E^-yE^（θ-1）E^（θ+y-θy），由复制动态方程稳定性可知：（1）当x=C时，F（z）≡0，此时z取任意值，方程都处于稳定状态，铁路部门既可以选择策略Rj，也可以选择策略Ri。（2）当x≠C时，F（z）=0，分两种情况讨论。①当00，此时z=0为稳定状态，即当政府选择策略Gj的概率小于C时，铁路部门将选择策略Ri。②当C0，F′（1）<0，此时z=1为稳定状态，即当政府选择策略Gj的概率大于C时，铁路部门将选择策略Rj。铁路部门的决策演化动态图如图4所示。

3 博弈稳定策略分析

由式（3）、（6）、（9）联立可得政府、港口部门、铁路部门三方的复制动态方程组。

该演化过程中存在9个均衡解：

E1（0，0，0）、E2（0，0，1）、E3（0，1，0）、E4（1，0，0）、E5（1，1，0）、E6（1，0，1）、E7（0，1，1）、E8（1，1，1）、E9（x0，y0，z0）。由于演化博弈稳定解一定是严格的纳什均衡，而E9（x0，y0，z0）为非渐进稳定状态，因此不予考虑。把其他8个均衡解分别代入雅可比矩阵，求解各个均衡解的特征根（见表2），并判断其稳定性（见表3）。

由李雅普诺夫间接法可知，特征根均为负数时，该均衡解存在局部稳定性，因此根据表2特征根的取值假设存在8种情形，分别讨论不同情形下各均衡解的稳定性，如表3所示。

由表3可知：在情形1下，政府、港口部门和铁路部门合作投资建设水铁联运专线将获得更大收益，此时系统存在演化稳定策略E8（1，1，1）;在情形2下，政府、港口部门和铁路部门依托原有业务将获得更大收益，此时系统存在演化稳定策略E1（0，0，0）;在情形3下，政府将独立投资建设水铁联运专线，发展当地经济从而获得更大收益，此时系统存在演化稳定策略E4（1，0，0）;在情形4下，政府和港口部门合作投资建设水铁联运专线将获得更大收益，此时系统存在演化稳定策略E5（1，1，0）;在情形5、6、7下，系统不存在演化稳定策略;在情形8下，港口部门将独立投资建设水铁联运专线，扩大港口运输范围，提高港口集疏运能力，从而获得更大收益，此时系统存在演化稳定策略E3（0，1，0）。

4 算例分析

经过前文对政府、港口部门和铁路部门三方演化博弈行为以及演化稳定解的分析，得出E1（0，0，0）、E3（0，1，0）、E4（1，0，0）、E5（1，1，0）、E8（1，1，1）这5个解在不同条件下能够成为演化稳定策略。下文运用MATLAB进行数值仿真分析，进一步验证系统的演化稳定策略。

（1）均衡解E1（0，0，0）数值仿真分析。

由前文可知，均衡解E1（0，0，0）在情形1下将成为演化稳定策略，因此假设

α=0，β=0，θ=0，ΔE=2，C=1，E1=7，C1=5，E2=5，C2=3，E3=5，C3=3。数值仿真见图5，其中：纵轴p表示投资概率;横轴t表示迭代次数，用来表征政府、港口部门和铁路部门达到稳定策略的时间。由图5可知，无论x、y、z在（0，1）上最终取何值，当投资收益小于原有收益时，政府、港口部门和铁路部门最终将选择不投资建设水铁联运专线，验证了在该条件下E1（0，0，0）为演化稳定策略。

（2）均衡解E3（0，1，0）数值仿真分析。

由前文可知均衡解E3（0，1，0）在情形8下将成为演化稳定策略，因此假设α=0，β=1，θ=0，ΔE=4，C=1，E1=7，C1=5，E2=5，C2=3，E3=7，C3=3。数值仿真结果见图6。由图6可知，无论x、y、z在（0，1）上取何值，当港口部门的投资收益大于原有收益时，港口部门愿意独立投资建设水铁联运专线，水铁联运专线建成后將给港口部门带来巨大收益，验证了在此条件下E3（0，1，0）为演化稳定策略。

（3）均衡解E4（1，0，0）数值仿真分析。

由前文可知，均衡解在情形3下将成为演化稳定策略，因此假设α=1，β=0，θ=0，ΔE=4，

C=1，E1=7，C1=5，E2=6，C2=3，E3=7，C3=4。数值仿真结果见图7。由图7可知，无论x、y、z在（0，1）上取何值，当政府的投资收益大于原有收益时，政府愿意独立投资建设水铁联运专线，水铁联运专线建成后将带动当地经济发展，从而给政府带来巨大收益，验证了在此情形下E4（1，0，0）为演化稳定策略。

（4）均衡解E5（1，1，0）数值仿真分析。

由前文可知，均衡解E5（1，1，0）在情形4下将成为演化稳定策略，因此假设α=0.5，β=0.5，θ=0，ΔE=4，C=1，E1=6，C1=5，E2=6，C2=5，E3=7，C3=4。数值仿真结果见图8。

由图8可知，无论x、y、z在（0，1）上取何值，在政府和港口部门的投资收益都大于原有收益时，政府与港口部门合作能减少各自的投资成本，政府与港口部门合作投资建设水铁联运专线将会获得更大收益，验证了在此情形下E5（1，1，0）为演化稳定策略。

（5）均衡解E8（1，1，1）数值仿真分析。

由前文可知，均衡解E8（1，1，1）在情形1下将成为演化稳定策略，因此假设α=0.3，β=0.4，θ=0.3，ΔE=6，C=1，E1=6，C1=5，E2=6，C2=5，E3=7，C3=6.5。数值仿真结果见图9。由图9可知，无论x、y、z在（0，1）上取何值，在各主体的投资收益都大于原有收益时，政府、港口部门和铁路部门合作能减少各自的投资成本，政府、港口部门和铁路部门合作投资建设水铁联运专线将获得更大收益，验证了在此情形下E8（1，1，1）为演化稳定策略。

5 结 论

本文基于水铁联运涉及的主要利益者，建立了政府、港口部门和铁路部门三方水铁联运专线建设投资演化博弈模型，并通过理论证明结合数值仿真，分析了在有限理性条件下政府、港口部门和铁路部门的最终演化稳定策略。得到的主要研究结论包括：

（1）在政府的投资收益大于原有收益时，政府选择独立投资或合作投资水铁联运专线建设策略都能获得更大收益。

（2）在港口部门的投资收益大于原有收益时，港口部门选择独立投资或合作投资水铁联运专线建设策略都能获得更大收益。

（3）在铁路部门的投资收益大于原有收益时，铁路部门只能选择合作投资水铁联运专线建设策略才能获得更大收益。

参考文献：

[1]赵严， 何世伟， 黎浩东. 水铁联运发展模式及其运输组织研究[J]. 铁道运输与经济， 2010， 32（6）： 23-26.

[2]张国伍. “一带一路”的多式联运服务体系研究： “交通7+1论坛”第四十四次会议纪实[J]. 交通运输系统工程与信息，  2016， 16（5）： 1-13.

[3]张滨， 黄波， 樊娉. “一带一路”背景下我国海陆联运建设与发展[J]. 中国流通经济， 2015（6）： 96-102.

[4]武慧荣， 朱晓宁. 基于SD的集装箱海铁联运系统发展研究[J]. 重庆交通大学学报（自然科学版）， 2013， 32（3）： 529-533.

[5]吴厌. 海铁联运是物流业快速发展的必由之路： 对港口物流发展方式转变的思考[J]. 港口经济， 2010（7）： 33-35.

[6]叶泫蠲. 浅谈北部湾港海铁联运对国际贸易的积极作用[J]. 特区经济， 2019（3）： 104-106.

[7]黄起龙， 崔彦博， 刘晓雷， 等. 基于系统动力学的铁水联运港政府服务体系研究[J]. 铁道运输与经济， 2019， 41（4）： 57-62， 75.

[8]郭静妮， 贺政纲. 基于集装箱运输的水铁联运体系构建[J]. 交通运输工程与信息学报， 2018， 16（4）： 41-49.

[9]鄒涛. 集装箱水铁联运港口站平面布置探讨[J]. 工程建设与设计， 2019（12）： 146-148.

[10]YANG Yijia， ZHU Xiaoning， HAGHANI A. Multiple equipment integrated scheduling and storage space allocation in rail-water intermodal container terminals considering energy efficiency[J]. Transportation Research Record， 2019， 2673（3）： 199-209. DOI： 10.1177/0361198118825474.

（编辑 赵勉）