网架焊接空心球节点残余应力实测及数值模拟

王超群， 雷宏刚， 李 洋

(太原理工大学土木工程学院， 太原 030024)

在网架结构中，焊接空心球节点是应用最多的一种节点形式。自1965年刘锡良[1]研制成功焊接空心球节点之后，焊接空心球节点已成为中国网架结构中最重要的一种节点形式。这种节点是由两个热压形成的半球对接焊成了空心球，再将钢管杆件与空心球采用对接焊缝或者角焊缝连接[2]。在钢管上开合适坡口通过电焊与空心球节点连接。

由于焊接过程的不确定性，焊接结构的复杂性和随机性尤为显著。在焊接过程中，局部不均匀的加热和冷却、焊缝以及焊缝附近温度场间的耦合作用，使焊接构件内部产生分布不均匀的残余应力场。焊接残余应力的存在对结构与焊接接头的抗脆断能力、抵抗应力腐蚀开裂以及高温蠕变开裂也会有不同程度的影响，尤其对钢结构的疲劳强度[3-5]影响较大。

焊接残余应力的研究起始于20世纪30年代。目前，中外学者对于焊接残余应力的研究主要是对钢板[6]、等边角钢[7]、H型钢[8]、焊接钢管[9-10]和热轧工字型钢[11]等构件的焊接残余应力分布模式的分析。对于平板构件焊接残余应力分布模型能否应用于焊接空心球节点尚且未知。因此需要对焊接空心球节点进行试验研究，其中李洋等[12]研究了三种尺寸较小的焊接空心球节点球面焊趾处焊接残余应力大小和变化趋势。证明了节点整体处于自平衡，但对于较大尺寸节点没有深入探索，并且由于测点布置过少，因此没有揭示焊接空心球节点的焊接残余应力分布模式，需要进一步进行试验。大多数对于焊接空心球的研究是通过有限元软件进行数值模拟分析[13-16]。

基于此，现以广泛应用于网架结构的焊接空心球节点为研究对象，采用盲孔法[17]对焊接空心球节点管-球焊缝焊接残余应力进行试验测量，此外创新性地结合 Visual-Environment软件对节点焊接过程进行模拟[18-19]，从而得到整个构件的温度场和残余应力场。将试验数据和数值模拟结果结合，绘制焊接残余应力曲线对比分析。以期得到残余应力的分布规律，为工程实践中焊接空心球节点的加工提供参考依据。

1 焊接残余应力试验研究

1.1 试验概况及试验原理

所用试件编号为GQ1-1、GQ1-2、GQ1-3，3种焊接空心球节点均为Q235-B钢材，材料特性为：弹性模量E=2.06×105MPa，泊松比μ=0.33。试件规格如图1所示，试件实际图如图2所示。试件具体参数如表1所示。

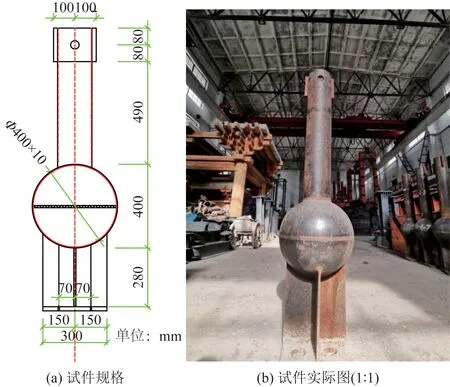
图1 焊接空心球节点Fig.1 Welded hollow ball node

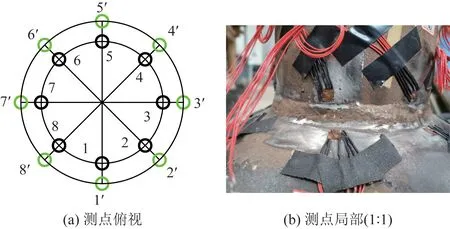
图2 球面管面测点布置图Fig.2 Spherical pipe surface survey point layout

表1 焊接空心球试件Table 1 Welded hollow ball specimen

焊缝焊趾附近焊接残余应力一般较大，并且容易发生破坏，为了得到较为准确的球面和管面焊接残余应力分布曲线，一般在靠近焊缝焊趾处布置测点。可以真实地反映焊缝焊趾处残余应力。

在球面、管面均匀布置8个测点，起始点为每个试件焊缝的假定起弧点，球面的测点编号为1′～8′，管面的测点编号为1～8，每个试件共16个测点。测点位置图如2所示。此外，孔间距的大小很大程度影响数据的准确。孔间距越小，对焊接残余应力的释放影响越大。标准要求一般相邻孔间距要大于5～8倍的孔径。

采用盲孔法测量焊接残余应力，试验中使用CM-2B TCP通道静态电阻应变仪， ZS-ⅡA型钻孔装置，三向电阻应变花BX120-2CA，电阻值为(119.8±0.1)Ω，灵敏系数为2.08%±1%，钻头采用Φ1.5 mm的麻花钻，所钻孔径1.5 mm，孔深2 mm。

由于焊接残余应力的主应力方向未知，所以试验采用45°、90°的三向应变花。应变花示意图如图3所示，实际应变花打孔位置如图4所示。

δ1和δ2为残余主应力；ε1、ε2、ε3为三向应变花位置；r1、r2、r3为测点距离应变花起点、中点、最远端的距离图3 三向应变花示意图Fig.3 Schematic diagram of a three-way strainer

图4 应变花打孔位置(1∶1)Fig.4 Strain relief punch locations

三向应变花测量得到钻孔前后的应变值ε1、ε2、ε3。计算简图如图5所示。

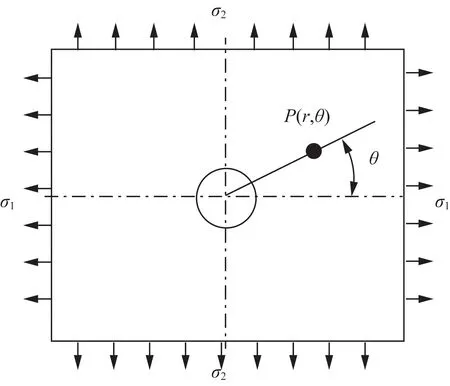
σ1和σ2为残余主应力；P为任意一点的位置图5 盲孔法残余应力计算简图Fig.5 Calculation of residual stress in blind hole method

通过数学公式推导(A、B为应变释放系数)，以应变ε反推应力σ：

(1)

得到焊接残余主应力σ1、σ2后，即可通过弹性力学坐标变换得到测点处径向和环向焊接残余应力，如式(2)所示：

(2)

式(2)中：σρ为径向应力；σθ为环向应力；τρθ为剪应力。

1.2 应变释放系数

应变释放系数采用计算方式和标定试验确定。计算公式有以下两种[20-21]。

(1)利用常规公式[式(3)]进行计算：

(3)

代入数据可得：A=-0.113 5×10-6MPa，B=-0.329 4×10-6MPa。

(2)基于通孔应变释放系数的Kirsch理论解，考虑了应变片的尺寸。Kirsch理论解适用于通孔情况下的应变释放系数的计算，如式(4)所示：

(4)

对于盲孔法，由圣维南原理可知，在孔径d一定的条件下，孔深h增加，当h/d介于1.0～1.5时，释放应变基本保持不变，应变释放系数与通孔的 Kirsch 理论解接近。本试验中h/d=1.33，所以可近似使用 Kirsch 理论解计算。

代入数据得A=-0.118 75×10-6MPa，B=-0.342 60×10-6MPa。

目前盲孔法测量残余应力应变释放系数的方法大多采用基于通孔应变释放系数的Kirsch 理论解，对比两种方法可知所得结果较为接近。

标定试验一共有三组，材料均采用与母材相同的Q235B钢材，在每个试件同样的部位布置90°双向应变花，并根据盲孔法在应变中心钻孔，标定尺寸及应变花布置如图6所示，试验标定应变释放系数A、B根据三组试验测得平均值为：A=-0.125 9×10-6MPa，B=-0.352 5×10-6MPa。

图6 标定尺寸及应变花布置Fig.6 Calibration sizes and strain relief arrangement

对比理论值和实验值，其中应变释放系数 A 理论值为-0.118 75×10-6MPa，试验值为-0.125 9×10-6MPa，相对误差 5.6%；应变释放系数 B 理论值为-0.342 6×10-6MPa，试验值为-0.352 5×10-6MPa，相对误差 2.8%。可知，试验结果与理论分析结果吻合度较好，试验所得结果与理论解相近，最终本次试验应变片应变释放系数取：A=-0.118 75×10-6MPa，B=-0.342 60×10-6MPa。

2 基于Visual Environment的数值模拟

2.1 有限元模型的建立

根据实际的焊接空心球节点尺寸建立了完全相同的有限元模型，因为实际焊接过程中焊缝附近输入热量很大，所以在焊缝附近存在较大的温度梯度，同时考虑到软件模拟时间，焊缝及其附近热影响区域网格划分较细，而在距离热影响区较远的母材网格划分则较为稀疏。网格划分使用Visual Environment软件的Visual-Mesh，具体步骤是先为2D截面划分网格，然后将2D截面采用3DRelove功能旋转成体，模型建成后用Check功能检查单元质量进行局部调整。根据焊接空心球节点管-球对接焊缝尺寸，焊缝处采用4层9道焊[22-23]，每道焊道熔池长度均为10 mm，熔池宽度在3.6～7.2 mm，熔池深度在2～3.5 mm。宽度和深度均按照熔池要求和网格划分后尺寸测量选取，具体尺寸具体选取。整个模型划分后的单元总数为29 854，节点总数为39 897，这样的网格划分既提高了精度也保证了模拟时间，模型及焊缝网格划分如图7所示。网格划分后在Visual-weld模块中定义实际焊接方法，母材材料属性、焊缝、焊接线、焊接参考线、焊接起始点、焊接终止点、散热边界和边界条件。

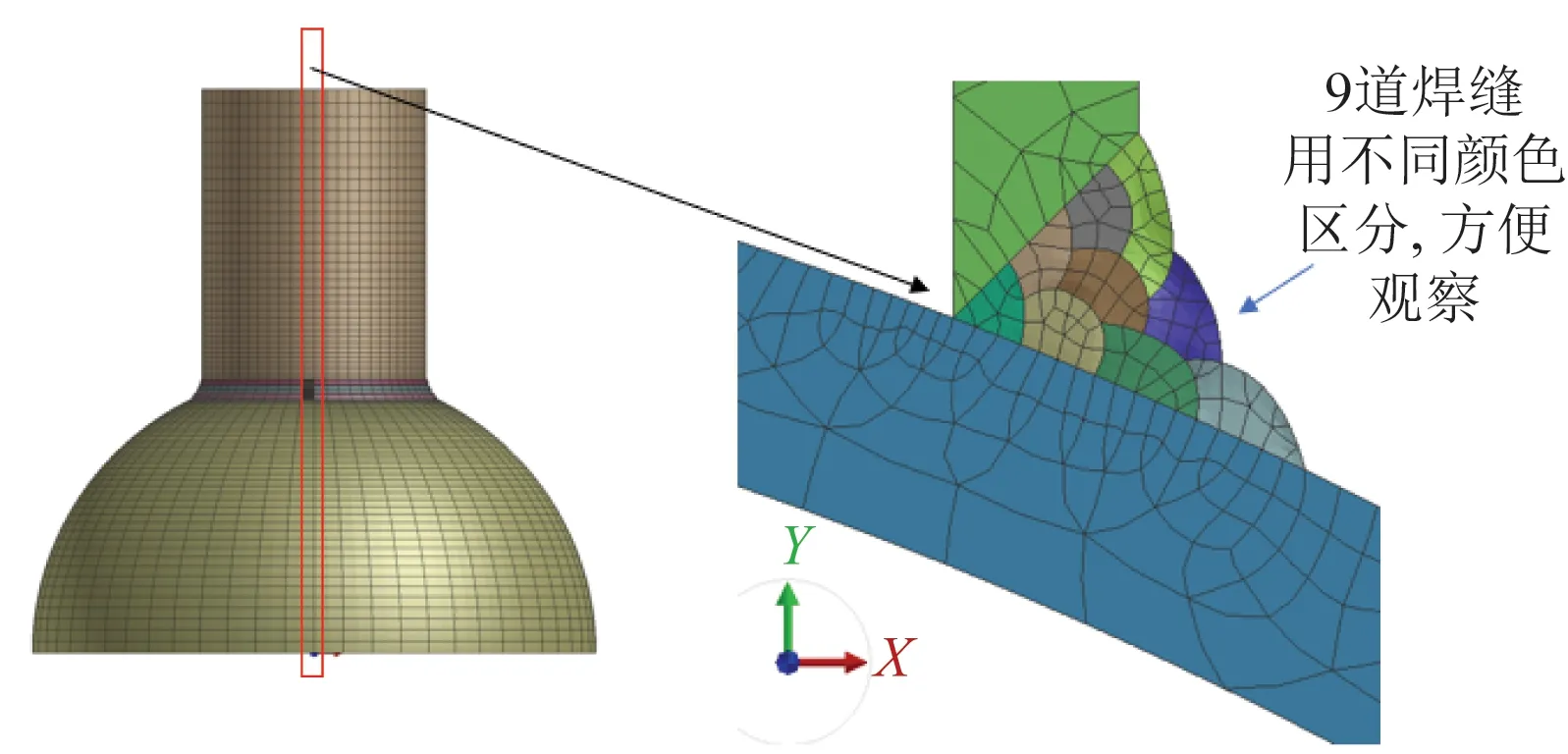
图7 网格划分示意图Fig.7 Schematic of finite element mesh

2.2 热分析与材料特性

在热分析过程，考虑到焊接温度场分析是属于非线性热传导问题，故作假定不考虑熔池在焊接过程的相变潜热，焊件初始温度为室温20 ℃，并且节点与环境仅进行对流换热。焊接热源采用Gol-dak提出的双椭球模型作为数值模拟的热源模型。在Visual Environment 软件当中选择手工焊方式进行焊接，焊接速度为9 mm/s，热源能量效率为0.8。此焊接方式的热源刚好为双椭球热源模型[24-26]，符合试验要求。每一条焊缝熔池宽度和深度根据具体尺寸测量确定。值得强调的是每一道焊缝焊接时都是在上一道焊缝冷却后再进行焊接，保证每一道焊缝焊接时不受上一道焊缝的热量影响。

设置母材和焊条时可将两种材料设置成同种材料。在材料库中选择ASTM A36钢材。该材料是美国标准中与中国标准Q235相对应的钢材。

2.3 边界约束条件

为了研究焊接空心球节点在温度变化及冷却后产生的焊接残余应力，在开始模拟时设置边界约束条件，避免构件出现刚性位移。本模型中焊缝单元尺寸控制在2 mm以内，远离焊缝处控制在9 mm以内，焊缝和非焊缝区之间设置过渡网格。设置边界条件为两端固定，Type设置为Rigid，On Deformed Geometry为yes，约束限制X、Y、Z三个方向移动和转动。与试验时边界条件一致，如图8所示。

红色为两端固定点图8 有限元模型边界条件Fig.8 boundary conditions of finite element model

3 模拟结果

3.1 焊接温度场分析

根据焊接空心球节点模型在焊接过程中不同时刻构件温度场变化云图，可以清楚地从温度场云图中看到熔池形状、最高温度与最低温度位置。在焊接过程中4个典型时间点的温度场的温度分布云图如图9所示。4个时间点分别为第1道焊缝开始焊处，2层第3道焊缝焊接终止点，3层第6道焊缝焊接终止点，4层第9道焊缝焊接终止点处。由于每一道焊缝焊接开始均在上一道焊缝冷却后进行，所以温度场的叠加影响较小，提高了残余应力的计算精度。

由图9看出，随着时间的变化，焊接热源在不断移动，焊接热源靠近时，该区域的温度迅速升高，当焊接热源离开时，该区域温度会迅速下降，最终趋于稳定。焊接的整个过程，焊缝不同的部位都要经历升温、降温、冷却、常温，所以温度应力场相当复杂。

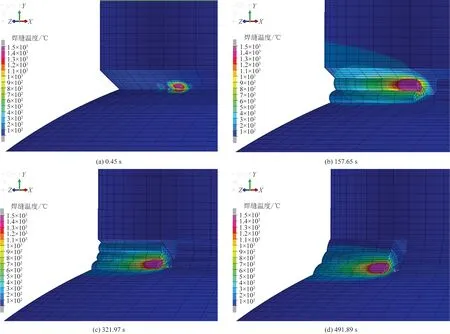
图9 温度场分布云图Fig.9 Nephogram of the temperature field distribution

3.2 焊接应力场分析

焊接时焊缝温度急速升高然后骤降，涉及材料的塑性及非线性，较为复杂。焊接过程中焊点周边温度一般超过1 500 ℃，钢材会产生塑性变形，当焊接结束后，产生塑性变形的部分不均匀冷却收缩受到约束而产生内应力即焊接残余应力。

在Visual-Weld模块可对焊接应力场进行计算与分析，以此研究钢管-焊接空心球节点管-球焊缝处残余应力的分布规律。通过Visual-Viewer模块查看残余应力分布云图，如图10所示。需要特别说明的是钢管采用的是柱面坐标系，空心球采用的是球面坐标系。

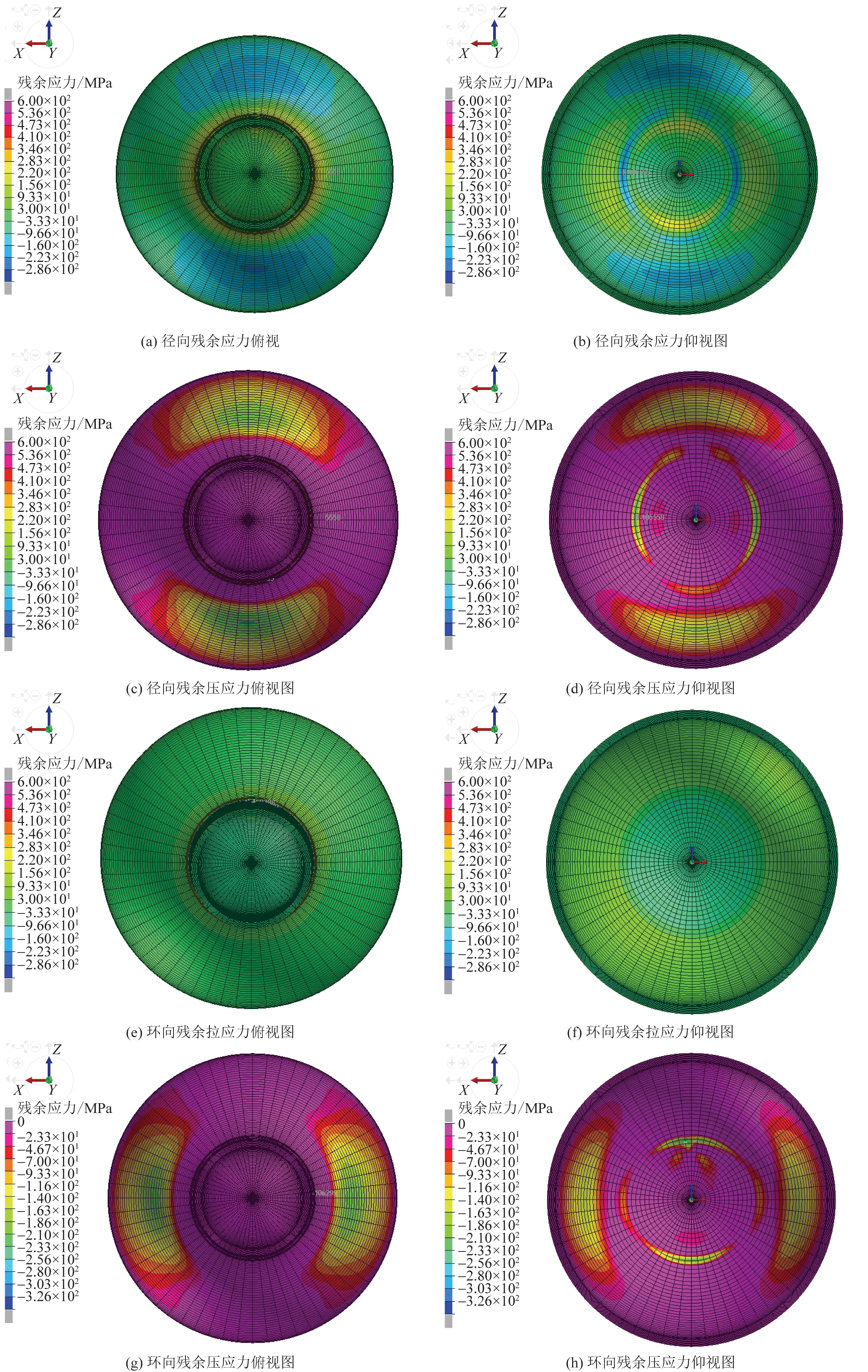
图10 焊接残余应力分布云图Fig.10 Tube-ball weld at the radial and circumferential welding residual stress

由图10可以看出，无论是径向残余应力还是环向残余应力在球面焊缝焊趾处和管面焊缝焊趾处均以残余拉应力为主并且由于热量大量输入，导致焊缝焊趾处残余拉应力较大。而在球面距焊缝较远处内外壁处和空心球内壁相对应焊缝焊趾处则是以残余压应力为主，整体应力分布呈现随机性。整体构件呈自平衡状态。

4 试验和模拟结果对比分析

有限元模拟与试验结果对比分析是基于试验测点与模拟路径一致性。在有限元模型球面焊趾和管面焊趾处取同样测点与试验结果进行对比并绘制曲线。

根据材性试验，本试验所用的钢材实际钢材屈服强度是268 MPa。

将计算应力与钢材屈服强度比值(σθ/σy)为纵坐标，与起弧点夹角作为横坐标绘制曲线。三种试件球面焊趾、管面焊趾处焊接残余应力分布曲线及对比图如图11所示。

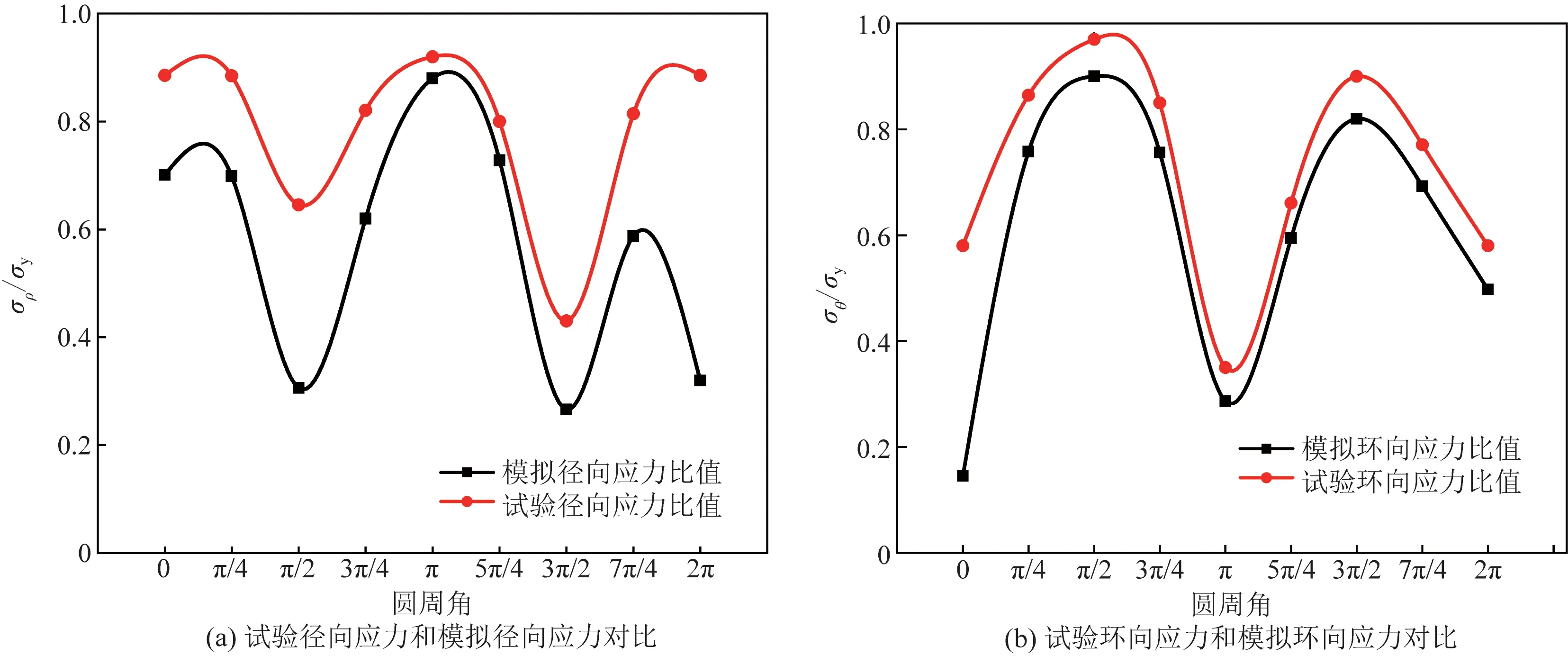
图11 球面焊趾处径向、环向残余应力对比分布曲线Fig.11 Comparison of radial and cyclic residual stress distribution curves at spherical weld toe

(1)试件GQ1-1。GQ1-1空心球焊缝焊趾处残余应力对比图如图11所示。

GQ1-1钢管焊缝焊趾处残余应力对比图如图12所示。

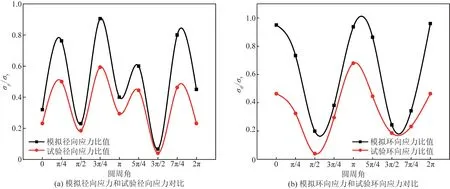
图12 管面焊趾处径向、环向残余应力对比分布曲线Fig.12 Contrast distribution curves of radial and cyclic residual stresses at the welded toe of a steel pipe

(2)试件GQ1-2。GQ1-2空心球焊缝焊趾处残余应力对比图如图13所示。

图13 球面焊趾处径向、环向残余应力对比分布曲线Fig.13 Comparison of radial and cyclic residual stress distribution curves at the spherical weld toe

GQ1-2钢管焊缝焊趾处残余应力对比图如图14所示。

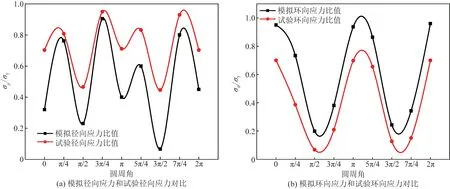
图14 钢管焊趾处径向、环向残余应力对比分布曲线Fig.14 Contrast distribution curves of radial and cyclic residual stresses at the welded toe of a steel pipe

(3)试件GQ1-3。 GQ1-3空心球焊缝焊趾处残余应力对比图如图15所示。

图15 球面焊趾处径向、环向残余应力对比分布曲线Fig.15 Radial and circumferential residual stress distribution curves at spherical welded toe

GQ1-3钢管焊缝焊趾处残余应力对比图如图16所示。

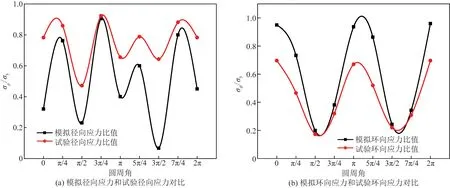
图16 钢管焊趾处径向、环向残余应力对比分布曲线Fig.16 Contrast distribution curves of radial and cyclic residual stresses at the welded toe of a steel pipe

通过以上对比可以发现：

(1)球面焊趾处残余应力。径向残余应力有限元模拟结果在(0.27～0.88)fy(fy为钢材的屈服强度)，呈周期分布，径向残余应力最大值为206.8 MPa；环向残余应力有限元模拟结果在(0.146～0.9)fy，也呈周期分布，环向残余应力最大值为211.5 MPa。GQ1-1、GQ1-2、GQ1-3球面径向残余应力试验值分别在(0.43～0.98)fy、(0.41～0.93)fy、(0.45～0.96)fy，径向残余应力最大值分别为230.3、218.55、225.6 MPa；环向残余应力试验值分别在(0.35～0.97)fy、(0.09～0.7)fy、(0.13～0.66)fy，环向残余应力最大值为227.95、164.5、154.9 MPa。

(2)管面焊趾处残余应力(以计算应力值与钢材屈服强度的比值表征)。径向残余应力有限元模拟结果在(0.067～0.905)fy，且呈周期分布，径向残余应力最大值为212.68 MPa；环向残余应力有限元结果在(0.199～0.96)fy，也呈周期分布，环向残余应力最大值为225.6 MPa。GQ1-1、GQ1-2、GQ1-3径向残余应力试验值分别在(0.04～0.593)fy、(0.446～0.95)fy、(0.47～0.92)fy，径向残余应力最大值分别为158.9、254.6、246.56 MPa；环向残余应力试验值分别在(0.04～0.68)fy、(0.068～0.699)fy、(0.17～0.69)fy，环向残余应力最大试验值为182.24、187.332、184.92 MPa。

(3)残余应力实测值与计算值之间差值主要是基于以下几个方面：①焊接空心球热压成型过程中的初始残余应力未计入；②钢管成型过程中的初始残余应力未计入；③有限元模拟是将模型简化并理想化加工条件下进行，无法百分之百还原实际焊接状态，所以存在一定误差。

5 结论

以焊接空心球节点管-球焊缝焊趾附近焊接残余应力为研究对象，通过盲孔法试验测量其焊接残余应力值的大小，研究了应变片应力释放系数、应力曲线。同时借助Visual Environment焊接模拟软件对焊接空心球节点进行建模，分析其焊接温度场和应力场，并与试验结果进行对比，得出以下主要结论。

(1)根据温度场云图可知残余应力分布具有随机性和复杂性，焊缝焊趾及附近区域以残余拉应力为主，远离焊缝焊趾区域及空心球内表面区域以残余压应力为主，整个试件上焊接残余应力处于自平衡状态。

(2)试验与有限元计算结果表明：焊接空心球面焊缝焊趾处径向残余应力在(0.27～0.98)fy呈周期分布；环向残余应力在(0.09～0.97)fy呈周期分布。钢管管面焊缝焊趾处径向残余应力在(0.04～0.95)fy呈周期分布；环向残余应力在(0.04～0.96)fy呈周期分布。

(3)试验与有限元计算结果的规律性吻合较好，但数值差异的主要原因是：未计入焊接空心球以及钢管自身的初始残余应力，再加上有限元模拟的理想化。