面向精细化管理的停车需求短时预测

李林波，李 杨

（同济大学道路与交通工程教育部重点实验室，上海201804）

汽车产业的快速发展与城市空间资源的有限构成严重冲突，供需矛盾日益尖锐，停车难问题成为了各大城市的挑战。为缓解停车设施停车难现象、提高停车设施的利用率，精细化停车管理的理念在近些年来逐渐被大众所接受［1-2］。作为精细化停车管理中的一部分，停车诱导系统（parking guidance system）［3-4］能够缓解交通拥堵的有效办法，但停车需求短时的精准预测作为空余车位发布的关键技术并没有得到有效解决。

停车需求预测可分为宏观停车需求预测与微观停车需求预测，宏观需求预测方法主要有停车生成率模型、出行吸引量模型、交通量停车需求模型与多元回归分析模型等［1］，一般属于长时预测；微观需求预测则是针对某一设施，对某一时间内的停车需求进行预测，属于短时预测，由于环境条件基本稳定，预测精度相对较为准确，这一方面的研究主要分为单一预测模型［1，5-12］，以及组合预测模型［13-16］，较多采用的模型主要有ARIMA预测模型［5-6］、考虑时空相关性的多元自回归预测模型［7］、马尔科夫模型［8］、卡尔曼滤波模型［9］、传统的神经网络模型［10-12］、基于Cox比例风险回归模型［1］、模糊神经网络预测方法［17］、结合小波分析以及马尔科夫链有效的泊位占有率短时预测方法［16］、基于混沌和BP神经网络的复合预测方法［13］、基于小波变换的神经网络改进方法［15］、基于相空间重构及Elman网络的短时停车泊位预测方法［14］、基于BP神经网络与马尔可夫链融合的组合预测方法［18］等。上述研究虽取得了一定的成果，但依然存在着一些不足。首先，大多数研究仅仅只是将泊位占有率的历史数据导入模型中进行计算，而未曾深究停车需求在不同月份以及不同工作日间的差异性，而对于停车需求差异性的研究正是精细化停车管理所需要的，忽略数据间差异性的处理必然会导致预测误差偏高。其次，传统的神经网络难以对时间序列数据内在的关联性进行准确建模，其假设相邻的输入样本在时间维度上的独立性，事实上停车需求数据在时间维度上存在着较强的相关性，如何有效对于存在较强非线性与时间依赖性的停车需求数据进行有效建模尚待解决。本研究旨在解决现有研究所存在的上述两个不足，针对第一点，研究将深入挖掘停车需求数据中的差异性，试图将这种差异性的研究融入至停车需求的短时精准预测中。针对上述的第二点，本研究将尝试将GRU（Gated Recurrent Unit）［19］模型首次引入至停车需求预测中，作为近年普遍使用的循环神经网络之一［20-22］，GRU模型在保持了LSTM（Long Short-term Memory）效果的同时又使模型结构简单［19］。

1 数据收集及特征分析

1.1 数据说明及采集

选取2015.01—2015.12新华医院停车设施（三级综合医院，数据量约67.8万条，泊位数为425个）自动采集的停车数据进行分析，原始数据信息包含了以下四个方面的信息：车辆识别信息、停车记录信息、停车收费信息以及停车管理信息。停车场原始数据每条记录包含每辆车驶入、驶离停车场的具体时间点，以30min为间隔获得各时间范围内的出入场流量数据，再加上一时间点的在场车辆数，则可获得各时间点上的停车需求量。由于停车需求的矛盾主要产生在工作日，因此剔除非工作日以及节假日等数据，最终得到244d的正常工作日数据，每月有效的数据样本数如表1所示。

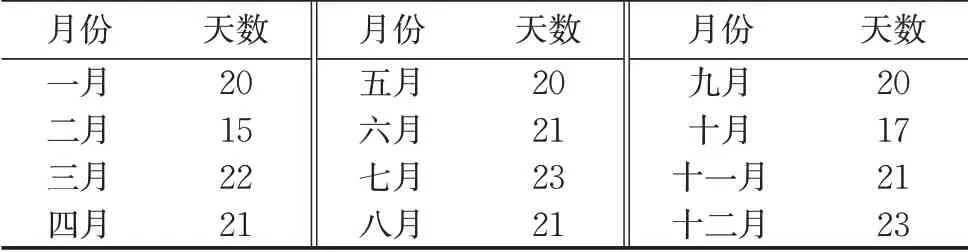
表1 新华医院每月有效工作日天数Tab.1 Sample data of parking demand in each month of Xinhua Hospital

1.2 停车需求特征分析

新华医院全年工作日时变曲线如图1所示，其各月实际泊位占用量每天时变趋势大致相似，呈现出上午、下午的停车需求高峰活跃期及晚间19：30左右的小高峰活跃期；在不同工作日间，停车需求的时变曲线线型非常相似，并且每日停车需求时变曲线重合度很高，呈现出稳定性的特征［2］。为研究停车需求在不同月份之间的差异性，采用聚类分析将12个月的停车需求划分四类（1—3月/7—8月/4—6月，9—11月/12月），其中1—3月的停车需求高于全年其余月份，接着为7—8月，其次为4—6月和9—11月，12月的停车需求要略低于全年其余月份。

图1 新华医院全年间停车需求时变拟合曲线Fig.1 Time-varying curves of parking demand grouping by months of Xinhua hospital.

为研究新华医院停车需求在不同工作日间的差异性，选取4—6月份每天6：00—22：00的数据，按周内各工作日（每周一、周二、周三、周四、周五）对泊位占有率时变曲线进行分组，得到五组的拟合曲线如图2所示。

图2 新华医院周内工作日间停车需求时变拟合曲线1Fig.2 Time-varying curves of parking demand grouping by different working days.

可以发现：①每周一的拟合曲线振幅要高于其它工作日的拟合曲线；②每周五的拟合曲线在14：00之后出现逐渐下降的趋势，且振幅最低；③每周二、周三及周四的拟合曲线基本重合，停车需求特征非常稳定，可划分为一组。在此基础上进行组间归并，最终划分为三组：周一为需求较高的一组；周二、周三、周四为需求较为稳定的一组；周五为需求在午后出现下降的一组，三组拟合曲线如图3所示，显然，停车需求在不同工作日间也存在着一定的显著差异性，因此，在面向精细化停车管理过程中，对停车需求的精准预测，有必要依据周内工作日的差异性对停车需求数据进行分组建模，以进一步提高模型预测的精度。

图3 新华医院周内工作日间停车需求时变拟合曲线2Fig.3 Time-varying curves of parking demand after regrouping by different working days

2 停车需求预测方法

2.1 GRU模型

LSTM模型［23］是循环神经网络RNN（recurrent neural network）的一种特殊形式，有着与RNN类似的链式形式，不仅能记忆之前时刻隐藏层的计算结果，对于时间序列有着很强的学习能力，并解决了RNN存在着的梯度消失和面临长期依赖的挑战等问题［23］。GRU［24］作为LSTM的变形，其内部单元与LSTM内部单元相似，但GRU模型将忘记门和输入门合成了一个单一的更新门，在保持了LSTM效果的同时又使模型结构简单［24］，其细胞结构如图4所示。

图4 RNN及其变形细胞单元结构Fig.4 Structure of RNN,LSTM,GRU cells

2.2 GRU模型原理

相比于长短期记忆神经网络，门控循环单元神经网络的循环结构只有两处，由决定保留多少当前输入信息xt的更新门以及控制前一时刻的输出ht-1对当前输入xt的影响的复位门组成。门控循环单元神经网络具体的计算步骤如下：

（1）当前输入信息xt与前一时刻的输出ht-1经由更新门输出得一个0～1之间的数值，其中0表示完全舍弃输入信息，1表示完全保留输入信息，计算如下：

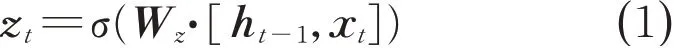
（2）当前输入信息xt与前一时刻的输出ht-1经由复位门输出得一个0～1之间的数值，同时tanh层会创建的新的候选值向量h͂t，计算如下：

（3）由更新门输出作为权重向量，前一时刻的输出ht-1与候选向量h͂t通过加权平均得到此时刻的输出值ht，计算如下：

式中：[∙]表示两个向量相连；∙表示矩阵的乘积；zt代表更新门的输出向量；rt代表复位门输出向量；h͂t代表此时刻的候选向量；ht代表此时刻输出向量；xt代表此时刻输入向量；W代表权重向量。

3 模型验证

采用新华医院停车场2015年4月1日至2015年6月12日中工作日数据作为训练数据集，采用2015年6月15日至2015年6月19日的数据作为测试集（共165个数据点），泊位占有率数据的时间段为工作日早上6：00至晚上22：00。同时根据第一节中周内各工作日时变曲线存在的差异性，将新华医院的训练数据划分为3组（周一；周二、三、四；周五），利用每一组的历史数据预测下一周这一组相对应的一天或者几天的泊位占有率数据，从而得到周内各日分时刻的泊位占有率预测值。除上节中所提及的参数，在对停车需求进行短时预测中，还需设定另一个重要参数“时间窗口”，是指将过去一段时间内的观测值作为下一个时刻观测值的特征，时间窗口的长度称为Lookback，即用多个过去的观测值去作为模型下一时刻输入的特征。在训练数据时，可以调整不同的Lookback以获得最优的Lookback值。

为便于估计模型拟合数据以及预测数据的精确度，引入平均绝对误差（MAE）、标准误差（RMSE）以及平均绝对百分误差（MAPE）等三个指标衡量模型的预测精度。MAE指标能很好地反映预测值误差的实际情况；RMSE指标可以用来衡量观测值同真值之间的偏差；MAPE指标可以很好地反映预测误差偏离实际的程度。

3.1 模型验证

以新华医院每周一的历史数据为例（共10日，330个数据点），以2015年6月15日数据作为测试集，为防止模型产生过拟合和欠拟合，以2015年6月8日数据作为验证集。设定GRU模型只含有一个隐藏层，调整这一隐藏层中不同神经元的个数。由于1日中的泊位占有率的数据点共有33个，所以Lookback选取范围定为1～33，通过调整不同的神经元个数以及不同的Lookback来得到最优的模型参数。

模型训练的散点图如图5所示，横坐标为不同Lookback的取值，纵坐标为不同Lookback大小以及不同神经元个数对应下的MAPE值，可以发现：随着Lookback逐渐增大，MAPE值呈现出逐渐下降的趋势。当Lookback在1～10之间时，模型在不同神经元下的MAPE值均较大。这主要是由于Lookback过小，模型输入数据的特征过少，模型能学习到的信息过少，从而预测误差最大。而随着Lookback逐渐增加时，模型的预测精度逐渐增加，当Lookback在11～13之间，模型在不同神经元下均能保持较低的MAPE值。这说明随着数据特征的逐渐增加，模型很好地学习了时间序列数据，最终标定第1组数据的Lookback为12，神经元个数为70。

图5 GRU训练MAPE散点图Fig.5 MAPES of training results of GRU model

按照上述方法标定第2组、第3组的历史数据所对应的模型并获得其相应在测试集上的误差。最终得到3组数据相应所标定的模型以及3组历史数据分别在其测试集上的误差，如表2所示。可以发现：模型在3组测试集上的MAE值分别为11.11、13.51、14，41；RMSE值分别为13.76、18.30、17.77；MAPE值分别为5.13%、6.06%和8.63%。

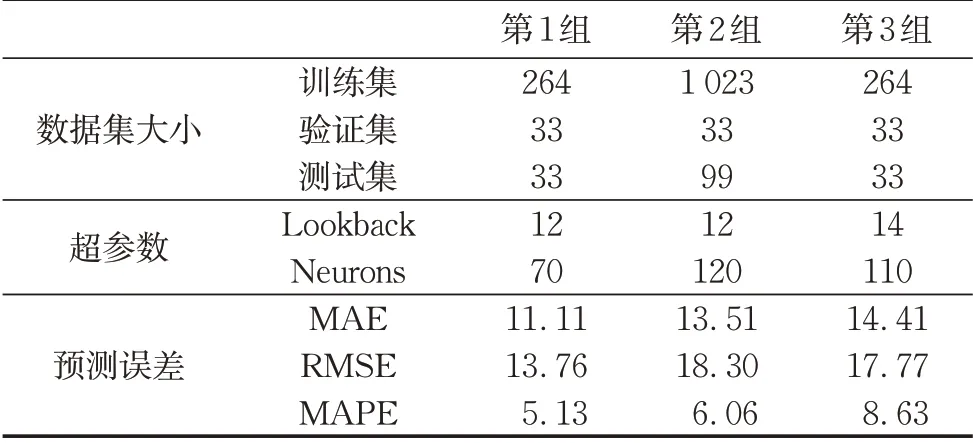
表2 GRU模型不同分组预测结果Tab.2 Results of different groups using GRU model

3.2 模型对比分析

为评估提出的预测方法，比较未分组情形下采用ARIMA模型、传统BP神经网络以及GRU模型的预测精度，模型定阶过程如下所示：①在ARIMA模型中，对二阶差分后的停车泊位占有率数据进行ADF（augmented Dickey-Fuller Test）检 验，得 到ADF值为-21.618，均小于1%，5%，10%所对应的值（-3.434，-2.863，-2.567）。之后，观测序列自相关系数和偏自相关系数，根据AIC（akaike information criterion）信息最小原则，模型定为ARIMA（8，4，2），此时AIC值为14 562.86。最后，对模型的残差进行Durbin-Watson检验，所得到的值为2.039，同时，残差序列通过Ljung-Box检验。②在传统BP神经网络模型中，同样设定一层隐藏层，学习率为0.01，交叉验证比例为0.33，Dropout（随机失活）参数值设置为0.3，优化函数选用Adam，输入维度为17，隐藏层神经元个数为150。③在GRU模型中，同样设定一层隐藏层，学习率为0.05，交叉验证比例为0.33，Dropout同样设为0.3，优化函数选取为RMsprop，Lookback参数为15，神经元个数为80。

综上，共对比分析4组情形，预测结果如表3以及图6所示，其中3组为不同模型未分组情形下的预测结果，最后1组为考虑了停车需求在周内日间差异性并对数据进行分组预测后的预测结果，可以发现：①在未分组情形下，ARIMA模型的预测精度最低，其MAPE达到了13.48%，而GRU模型的MAPE值仅为7.95%。②按停车需求的差异性对数据进行分组后，GRU模型的预测精度进一步提升，MAPE从7.95%降至6.45%。研究表明：①相比于传统神经网络以及ARIMA模型，GRU模型能够提供更好的预测精度。②在考虑了停车需求在周内日间的差异性并对数据进行分组预测后，GRU预测精度得到进一步的提升。

表3 不同模型预测结果Tab.3 Results of different prediction models

图6 实际停车需求值与本研究所采用的预测方法比较Fig.6 Comparison between actual parking demand and prediction value

4 结语

停车需求短时精准预测是精细化停车管理中的重要组成部分，特别是在停车诱导过程中，停车需求的精准预测可以极大地提升了信息发布的有效性，解决了停车诱导发布信息与车辆到达停车场后的实际信息不一致的困境。本研究在精细化停车管理的理念下，对停车需求在月内以及周内不同工作日的差异性进行了深入研究，研究表明停车需求在不同月份以及不同工作日间存在着显著的差异性，结果表明：周一为需求较高的一组；周二、周三、周四为需求较为稳定的一组；周五为需求在午后出现下降的一组。在此基础上，按照停车需求在周内日间的差异性对数据进行分组，并利用更简洁的GRU模型进行分组预测，研究表明在对停车需求进行分组预测后，模型的预测精度能够进一步提升。本研究可为停车诱导系统提供更为先进、更为精细化的预测方法。由于篇幅的限制，本文只针对工作日停车数据进行了阐述，实际上对于非工作日的预测有着同样的效果。值得注意的是，本文并未将天气因素考虑进来，同时可以考虑采用［20，25］深度学习中的其他预测方法进行交叉对比分析，构建组合预测模型来提高预测精度。

作者贡献说明：

李林波：相关概念及方案讨论，论文语言组织；

李杨：数据处理及分析，实验设计及初稿撰写。