基于混合算法的光伏MPPT优化

王文保，周振雄，彭红义，张志敏

(北华大学电气与信息工程学院，吉林 吉林 132021)

光伏发电不仅具有清洁高效的能源质量，还可作为优质储能电源削峰填谷，满足不同负荷随时间变化的电能需求[1].随着电力电子技术的逐渐成熟，光伏发电并网容量大幅增长，传统算法的跟踪性能受到挑战.作为提高太阳能利用率的关键，提高光伏发电MPPT算法在启动速度、震荡幅度、全局搜索能力和跟踪精度上的性能，一直是学者们关注、研究的焦点.研究涉及多个方面：1)基于群的MPPT遗传和优化算法改进[2-4].其中，免疫萤火虫算法通过赋予萤火虫群体自我排除不良个体的能力，使虫群在移动时向最优个体集中，算法跟踪速度较快，但启动速度较慢；粒子群和自适应方法虽有较好的跟踪性能，但仿真模型过于简单，对3个及以上光伏组件并联的情况没有提及.2)基于样本训练的MPPT机器学习算法[5-6].该类算法在大容量PV阵列等复杂条件下难以对极端情况做出正确判断，并且缺少物理层面的解释.3)基于函数或微分差分式的数学算法[7-9].该类方法通过数学手段对PV阵列输出特性进行跟踪，忽略了高阶小量，加之传统仿真常用的光伏电池模型为数学模型，所得输出特性其实已经包含近似误差，因此，该方法的跟踪精度有待提高.4)基于拓扑优化和参数辨识的模型优化方法[10-13].该类方法把光伏电池的基本结构和参数作为起点，以优化PV阵列功率输出特性或改善MPPT动态跟踪效果为目的，具有一定研究意义，但由于PV阵列的拓扑结构和参数受并网容量和环境条件的影响很大，因此，目前难以在工程中应用.

为了在提高PV阵列MPPT算法启动速度的同时获得更小的震荡幅度、更好的全局搜索能力和更高的跟踪精度，综合上述算法的优缺点，本文提出一种由CVT、PSO和BFA 3种算法结合的混合算法.该算法由CVT算法提供当前环境条件下最大功率点对应的电压值，并将该电压值作为初始位置信息，在一定时间后切换至PSO-BFA结合算法；之后，以BFA算法的迁徙、复制和趋向过程为总体框架，用PSO算法更新细菌搜索速度，并引入自适应因子，以实现最大功率点跟踪，为光伏发电大容量并网系统提供一种MPPT配置思路.

1 局部遮阴下的PV阵列输出特性

光伏电池是太阳能发电的最小发电单位，其数学模型见图1.

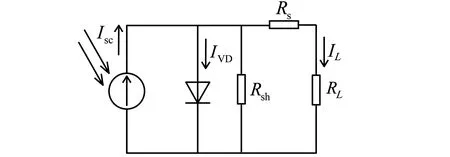
图1 光伏电池数学模型Fig.1 Mathematical model of photocell

由图1可得输出电流：

式中：IL和UL分别为负载侧输出电流、电压；Isc为电池介质外层电子受光照激发产生的电流；ID为二极管对应的电流；Rsh为分流电阻；Rs和RL分别为限流电阻和负载等效电阻；A为二极管因子；K为玻尔兹曼常数；t为电池温度.

ID、Rsh、Isc、A与温度和光照有关，工程上需简化处理.根据文献[3]搭建光电池数学模型，并构建基于3×3PV阵列的结构模型，见图2，相关参数见表1和表2.

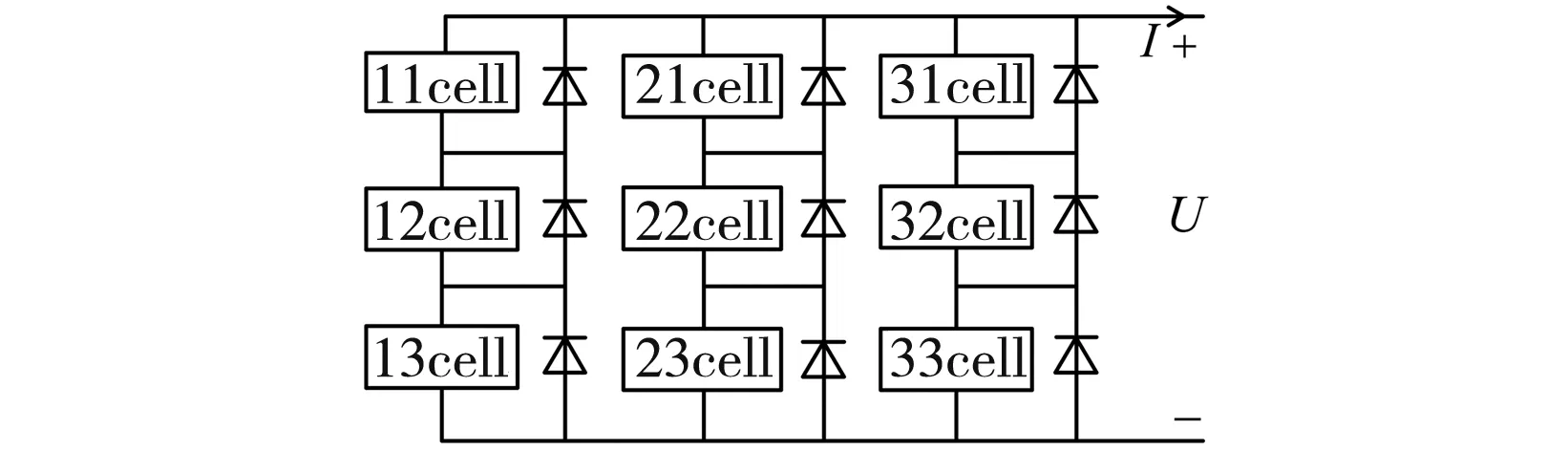
图2 PV阵列结构模型Fig.2 Simulation model of PV array

表1 光伏电池参数Tab.1 Parameters of photocell

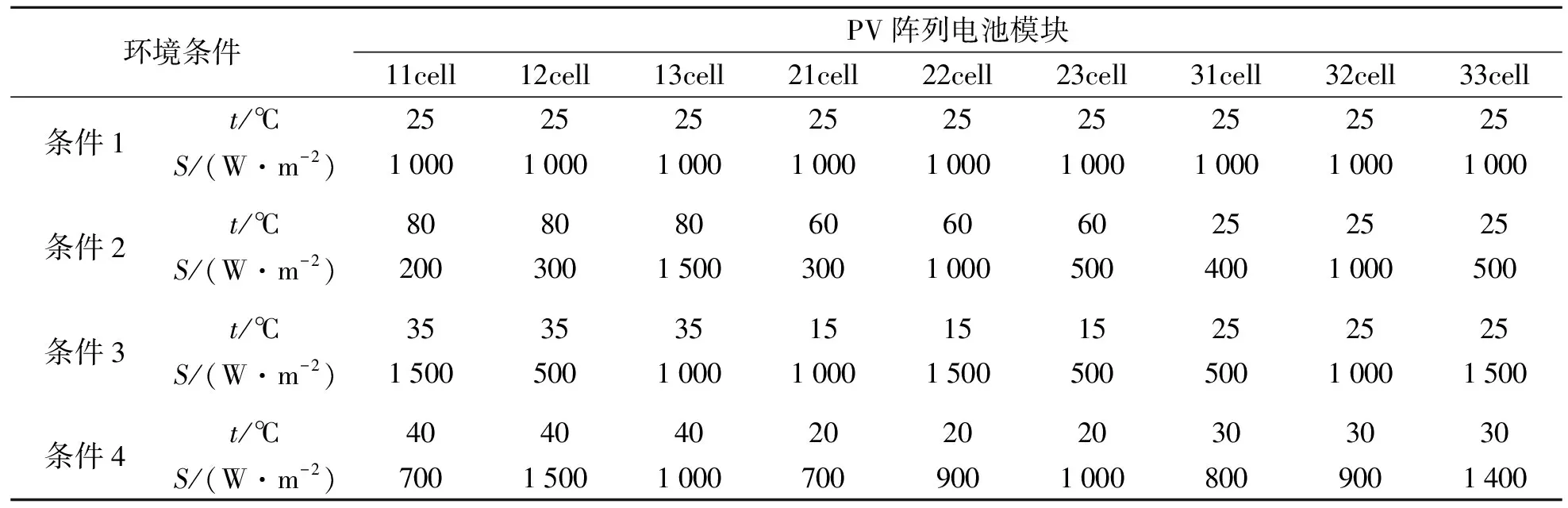
表2 PV阵列电池模块环境条件Tab.2 Environment conditions of PV array simulation

3×3PV阵列在4种条件下的输出特性曲线见图3，条件1为标准测试条件STC.由图3 a可知，3×3PV阵列在STC下的Uoc、Isc、Um和Im均为光伏电池的3倍.由于光伏电池部分被遮挡后的光照环境不同，因此会出现多峰情况，条件2、3、4即为最大峰值出现在不同位置的情形.

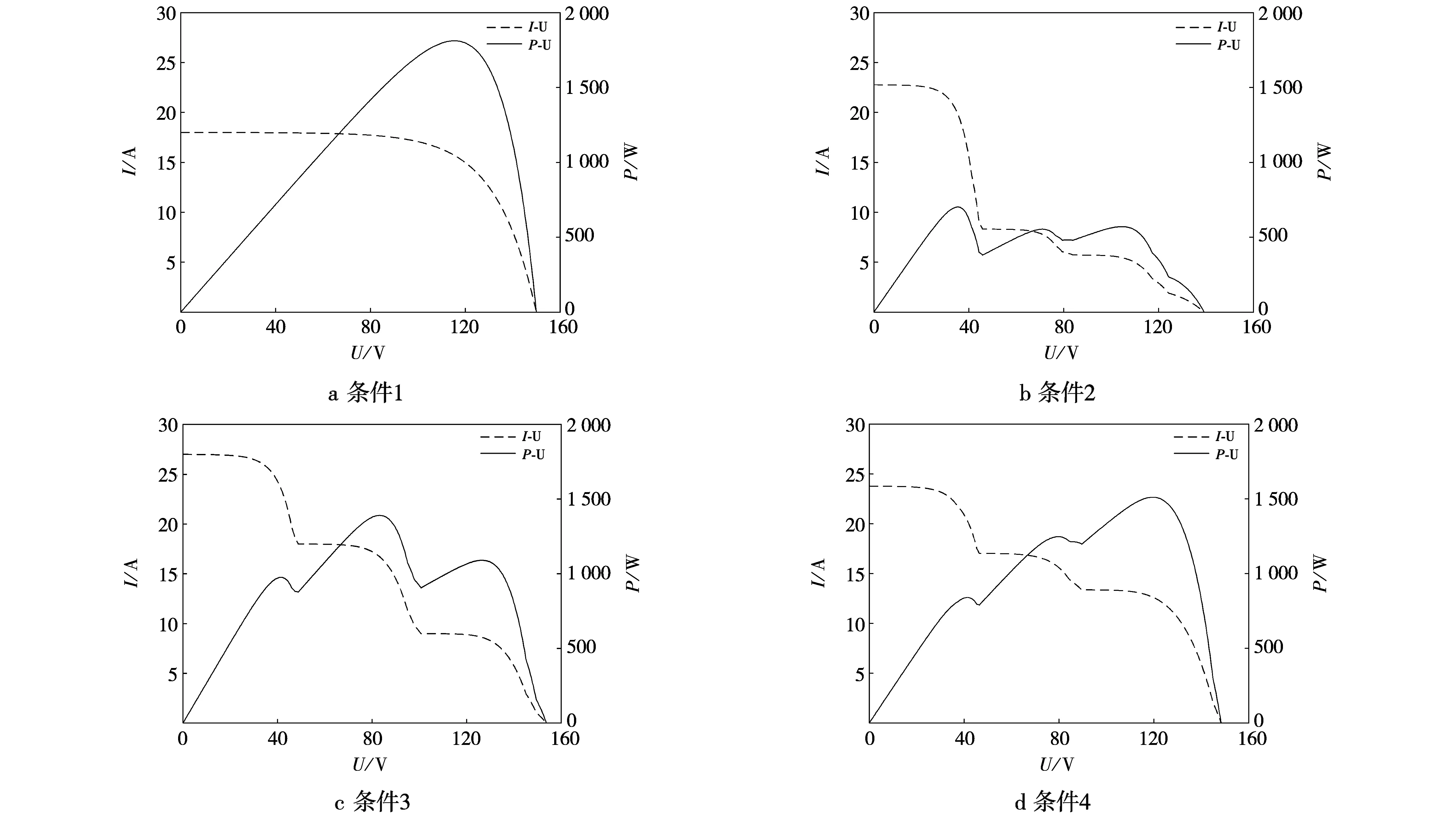
图3 不同条件下3×3PV阵列输出特性Fig.3 Output characteristic of 3×3PV array under different conditions

2 局部遮阴条件下PV阵列的MPPT混合算法

2.1 传统MPPT算法

根据电池串联数目的适应度，传统MPPT算法可以分为单峰值算法和多峰值算法.单峰值算法可迅速且精确地追踪到PV阵列的局部最大功率(GPP)，若PV阵列光照、温度等环境条件基本一致，则也可追踪到全局最大功率点(MPP).CVT算法通过预先判断MPP点的位置，以所得近似功率作为MPP，启动性能良好，但由于电压为定值，难以适应外部条件改变的情况；电导增量法INC利用功率-电压曲线的特点，可将追踪到的MPP限制在相邻两个步长的范围内，但无论是变步长还是定步长的搜索方式，都会有一定的搜索误差，且搜索速度慢；扰动观察法PSO在启动速度上不如CVT，且无法兼具速度与精度.为解决上述问题，有研究者提出了将传统单峰值算法相结合的新算法，但在PV阵列局部遮阴时，依旧存在将功率极大值错误地作为功率最大值的问题.

多峰值算法主要以PSO等遗传算法和BFA等优化算法为主，两种算法均能够在局部遮阴的情况下准确地获取最大功率值，但受迭代次数、迭代公式复杂程度的影响，算法跟踪速度较慢.遗传和优化算法都具有一定的记忆能力，在多峰值的全局搜索过程中不易局限于伪波峰.不同算法的迭代公式、循环嵌套层数均有差异.PSO算法在速度更新中考虑了局部最优解和全局最优解；BFA算法则从种群的角度考虑所有细菌，它们具有迁徙、复制和趋向的能力，能够增加个体随机性.

由此可见，上述算法并没有从启动速度、震荡幅度、全局搜索能力和跟踪精度4个角度同时考虑光伏阵列MPPT算法的综合性能.

2.2 自适应BFA算法

传统细菌觅食BFA算法由趋化、复制和驱散3个步骤组成.对具有初始位置和适应度值的细菌，首先需在一个菌落内进行趋化操作.趋化操作中，若更新后的适应度值低于更新前的适应度值，则对该细菌的速度进行翻转操作，否则正常前进.在一个菌落内每个个体细菌都进行了一轮趋化后，对该菌落进行复制操作，通常舍去适应度低的一半，将剩余的优秀细菌以分裂的形式复制出一个位置和适应度相同的细菌.最后，算法会根据概率有选择性地对细菌进行驱散，避免部分细菌受限于局部极大值点.

传统BFA算法的位置迭代式：

θi(j+1，k，l)=θi(j，k，l)+C(i)φ(j)，

式中：θi(j，k，l)为第i个细菌θi在经过j次趋化、k次复制和l次驱散后的位置；C(i)为前进步长；φ(j)为决定方向，根据适应度大小决定前进或反向翻转.

传统细菌觅食法在参数设置上固定，在其位置迭代式中，移动步长是定值，这会使收敛速度变慢.此外，细菌可以通过翻转操作获得良好的局部寻优能力，但表达式中未考虑细菌的全局跟踪能力，导致BFA算法存在局限在局部极大值点的可能.

本文将前进步长和驱散概率均改为自适应算法[3]：

(1)

(2)

在式(1)中，自适应步长C(i)以最大步长Cmax为基值，并依迭代的最大次数M和当前次数i进行自适应调整；在式(2)中，自适应驱散概率Ped(i)以初始驱散概率Pin为基值，并依据适应度的最大值Fmax、最小值Fmin和当前值Fi进行自适应调整.

2.3 传统PSO算法

传统粒子群PSO算法的位置和速度迭代式：

(3)

(4)

式中：k为迭代次数；Pbest和Gbest分别表示局部和全局最优值；参数c1、c2分别为学习因子；r1、r2为[0，1]间的随机数.

由式(3)、(4)可知，与BFA算法相比，PSO算法具有很好的全局寻优能力，但参数固定，同样存在难以兼具收敛速度和跟踪精度的问题.

2.4 CVT-PSO-BFA算法

传统CVT算法可在跟踪初期直接设定约0.8倍的开路电压值作为MPPT起始位置，缩短MPPT跟踪时间；传统BFA算法具有优异的局部搜索能力，同时在引入自适应因子后收敛速度更快；传统PSO算法则具有优异的全局搜索能力.因此，本文采用将PSO与BFA相结合的方法，得到如下位置迭代式：

θi(j+1，k，l)=θi(j，k，l)+C(i)φ(i)+

c1r1(Pbest-θi(j，k，l))+

c2r2(Gbest-θi(j，k，l))，

式中：C(i)采用式(1)的自适应算法，相应取值随迭代次数的增加而减小.

在最初一段时间内，利用CVT算法初步追踪环境条件4中的最大功率点.CVT-PSO-BFA混合算法流程见图4.

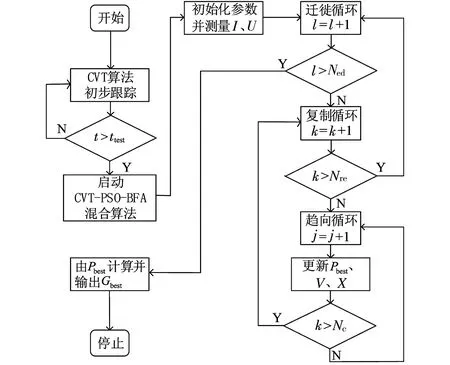
图4 CVT-PSO-BFA 混合算法流程Fig.4 Flow of CVT-PSO-BFA hybrid algorithm

2.5 仿真分析

基于Boost的最大功率跟踪系统见图5.其中，3×3PV阵列经Boost斩波电路与负载RL相连，MPPT模块通过实时计算PV阵列的端电压UPV和端电流IPV经控制器输出占空比D.Boost电路通过控制占空比D的方式，实现负载阻抗的实时调节，使其追踪光伏电池的输出阻抗，控制最大功率跟踪.电路中电容C1=100 μF，电感L=10 mH，电容C2=300 μF.

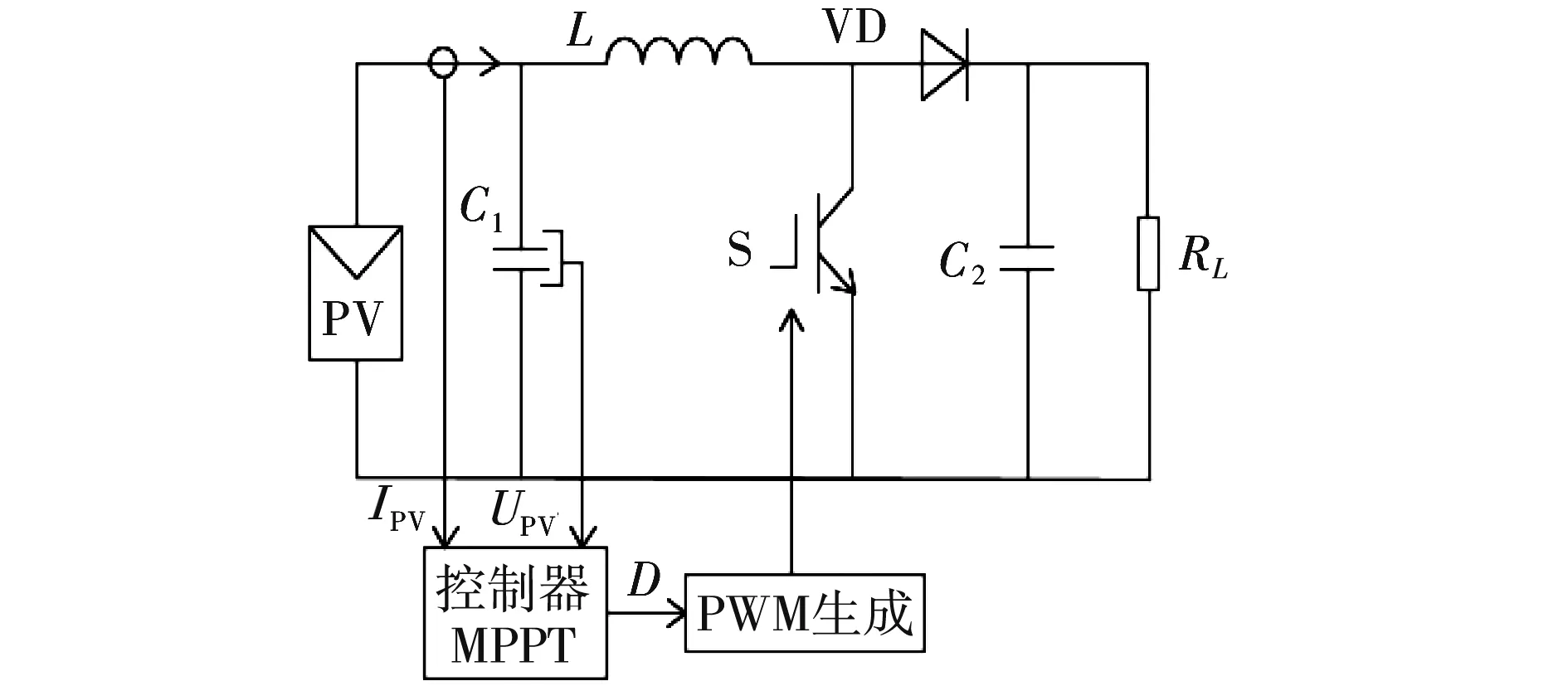
图5 基于Boost的最大功率跟踪系统Fig.5 Maximum power tracking system based on Boost

为了验证本文所提出CVT-PSO-BFA混合算法的有效性，以条件4为例，分析3×3PV阵列的输出特性，仿真结果见图6.由图6可知：CVT算法的确可有效缩短启动速度，且PSO算法与BFA算法结合后可有效提升功率跟踪精度.本文所提CVT-PSO-BFA新混合算法仅需0.043 s即可到达最大功率点，且跟踪功率值有所提升，说明新混合算法在启动速度、震荡幅度和跟踪精度上性能优异.

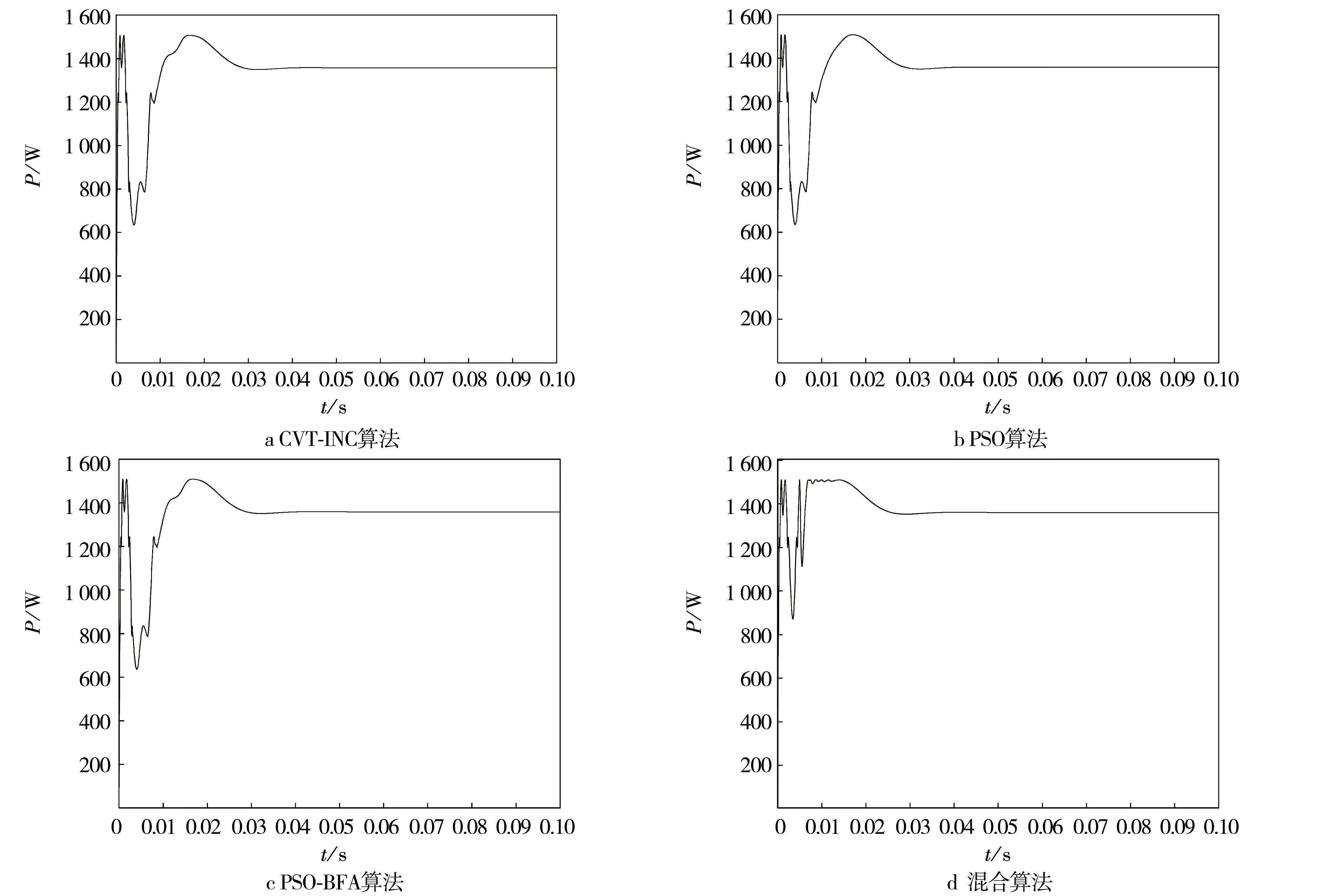
图6 3×3PV阵列在传统MPPT算法与MPPT混合算法下的功率输出特性Fig.6 Power output characteristics of 3×3PV array under traditional MPPT algorithm and MPPT hybrid algorithm

3 小 结

近年来，受环境及能源影响，光伏发电越来越受到重视，提高光伏转换效率有着非常重要的意义.本文在对比分析CVT-INC结合算法、PSO算法、PSO-BFA结合算法3种光伏MPPT算法的基础上，提出了CVT-PSO-BFA混合算法，并通过MATLAB进行了仿真验证.结果发现：本文提出的CVT-PSO-BFA混合算法具有更快的启动速度、更小的震荡幅度、更好的跟踪精度以及优秀的全局搜索能力.在外界光照不均匀的情况下，使用该混合算法可以避免陷入局部最优搜索，全局搜索能力增强，能有效寻找到最大功率跟踪点，提高了光伏发电效率.