密度锥削阵FDA雷达方向图特性分析

王 博， 陈楚舒， 张君鹏， 姜 杰

(1. 中国人民解放军95972部队, 甘肃酒泉 735300; 2. 空军工程大学防空反导学院, 陕西西安 710051)

0 引言

FDA通过在阵元间引入一个相比载频而言大小可忽略的固定频偏实现了具有更高自由度的时间-距离-角度三维相关波束指向[1-2]。FDA雷达波束的距离-角度-时间三维相关特性，与相控阵相比在抑制距离相关性干扰的过程中有着巨大的应用价值，因此得到了国内外学者的广泛关注[3-8]。目前，一维FDA结构的研究文献中大多按照均匀线性方式排布阵元，较少有关于不均匀阵列结构的分析研究[9-10]。不均匀阵列分为单元间距不均匀、激励幅度不均匀、激励相位递变不均匀三种类型。本文针对单元间距不均匀FDA雷达的方向图特性展开仿真分析，探讨密度锥削阵FDA雷达的方向图特性。从而为后续FDA雷达一维阵列结构设计的进一步研究奠定基础。

1 ULFDA结构

图1为一维均匀线性FDA(Uniform Linear Array FDA, ULFDA)的结构示意图[1]。

图1 ULFDA基本结构

设载波频率为f0，阵元n的辐射信号频率为

fn=f0+Δfn=f0+nΔf,

n=0,1,2,…,N-1

(1)

式中，Δf表示阵元间的频偏增量。窄带条件下，阵元n的发射信号可表示为

sn(t)=exp(j2πfnt),n=0,1,…,N-1

(2)

阵元n发射的信号到达远场观测点(R,θ)的信号表达式为

(3)

式中，R为参考阵元到目标点的距离，d为阵元间距。ULFDA在(R,θ)处电场强度的总和为

(4)

式中，fe(ω0+nΔω)表示天线方向性函数。

2 密度锥削阵FDA方向图特性分析

与ULFDA中阵元间距等量线性递增不同，密度锥削阵中越靠近参考阵元的阵元排布密度越大，越远离参考阵元的阵元排布越稀疏。图2为N阵元的一维密度锥削阵结构示意图[11-12]。

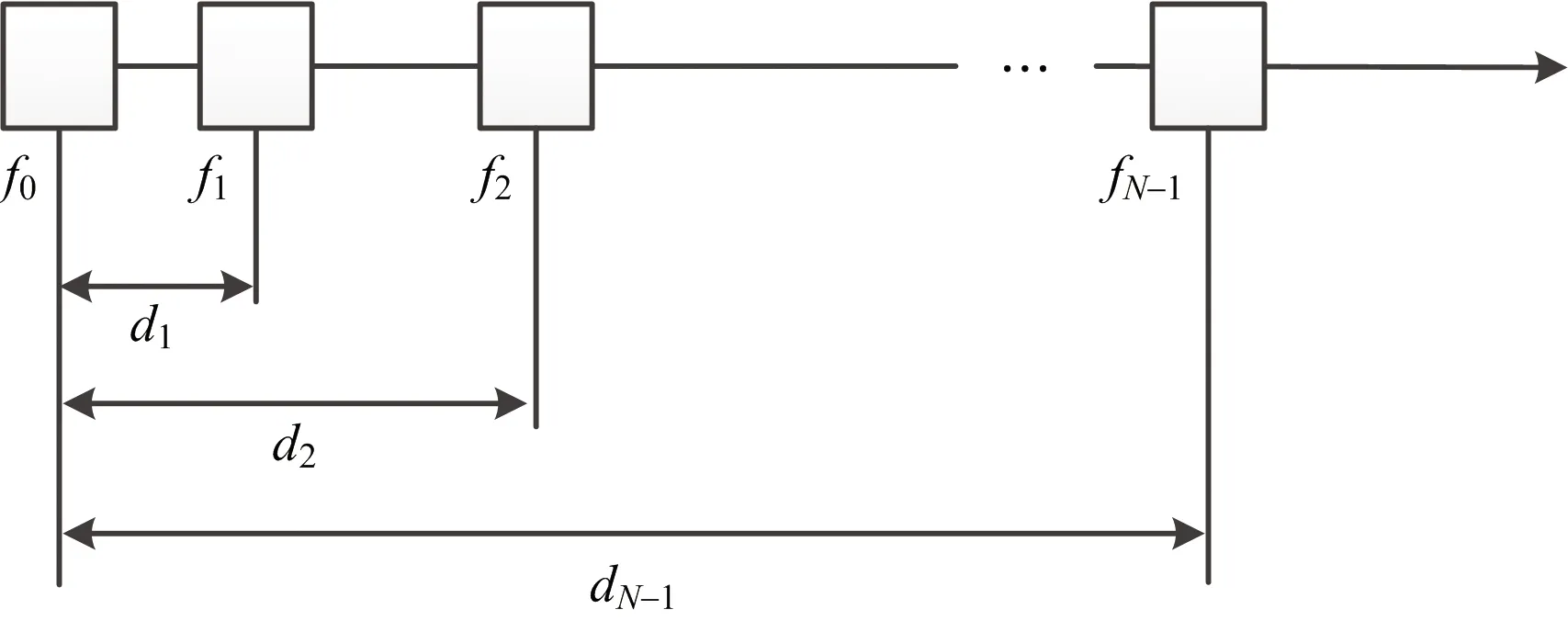
图2 密度锥削阵FDA结构示意图

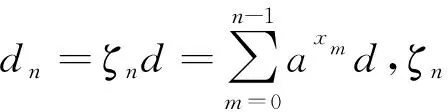
(5)

密度锥削阵FDA在(R,θ)处电场强度的总和为

(6)

由式(6)可知，密度锥削阵FDA在远场目标点处的波束形状与FDA雷达的频控函数Δfn、密度锥削阵间距递增因子a以及xm的函数形式有关。因此可以考虑通过控制上述函数从而得到相比于ULFDA“S形”波束性能更优的发射方向图。

取频控函数Δfn=nΔf，t=0 s，则密度锥削阵FDA相邻阵元的相位误差可表示为

Δψ=ψ1-ψ0=

(7)

式(7)中，当Δf=0时阵列退化为基于密度锥削阵的PA雷达结构；第二项表明相位差与频偏增量及目标距离有关；第三项表明密度锥削阵FDA仍然存在如何消除发射方向图中距离-角度耦合的问题。由式(7)可知,阵列扫描的等效视角可表示为

(8)

当θ=0°时式(8)等效为

(9)

对距离R求微分可得波束扫描角度随距离的变化率：

(10)

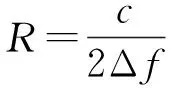
图3 频率分集阵列角度随距离变化关系

由式(8)可以简化得出

(11)

图4～5分别仿真了当阵面角分别为0°、30°时三种频偏增量取值时扫描角与距离的关系。

图4 扫描角与距离的关系(θ0=0°)

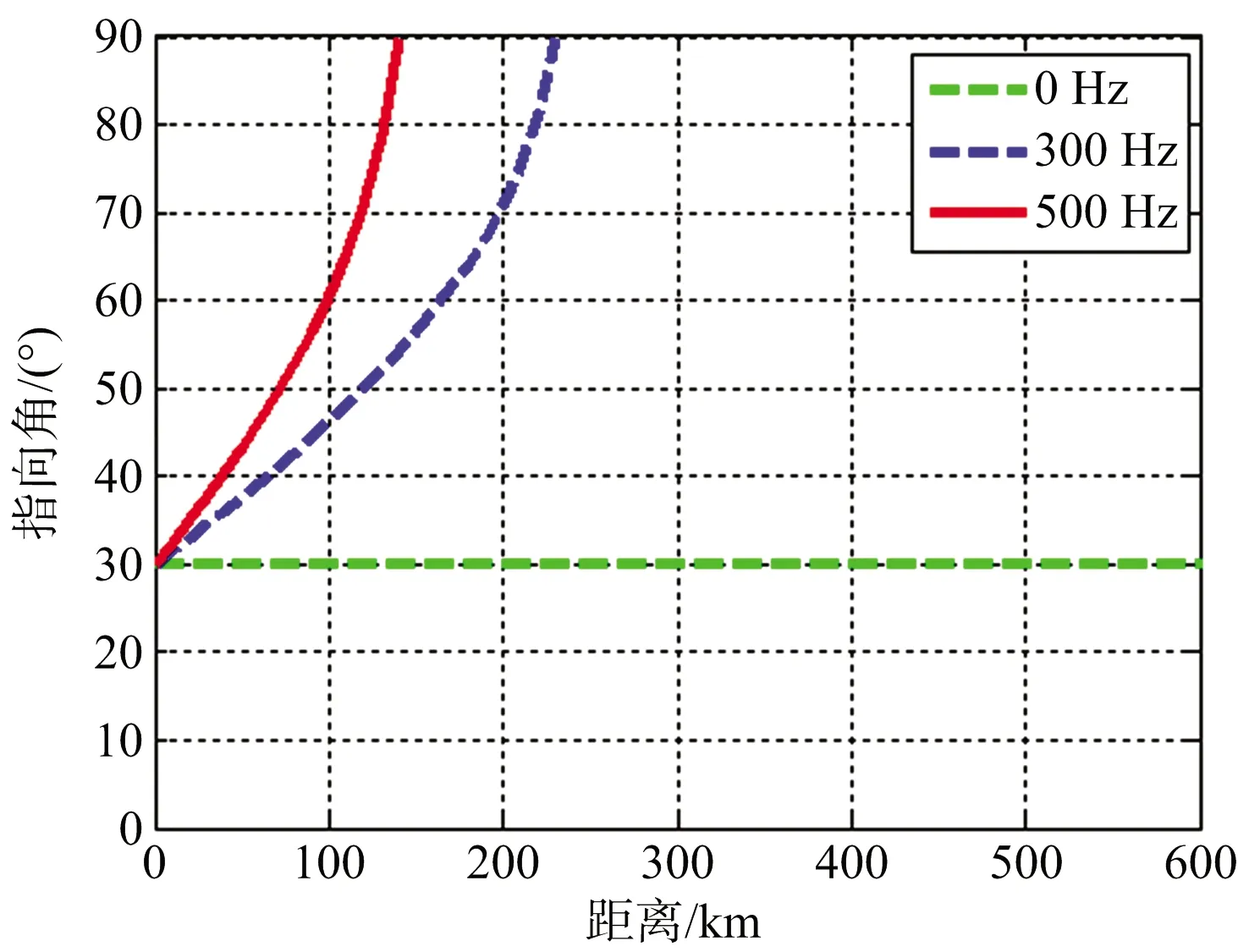
图5 扫描角与距离的关系(θ0=30°)

3 仿真验证

仿真验证本文分析的正确性，考虑一个10阵元的一维均匀线性阵列，阵元间距d=c/(2f0)，载频f0=1 GHz，阵元间频偏Δf=5 kHz。

仿真1： PA、ULFDA、log-FDA与密度锥削阵发射方向图的对比分析。

图6 PA的发射方向图

图7 ULFDA的发射方向图

图8 log-FDA发射方向图

图9 密度锥削阵FDA发射方向图

由图6～8可知，与相控阵波束指向只与角度相关而与距离无关不同，ULFDA发射方向图的波束呈现出距离-角度二维相关的“S型”，在抑制距离相关性干扰中具有应用的可能。但ULFDA波束图中的多极值问题以及距离-角度耦合问题都需要通过频控函数和阵列结构的设计消除。本文将密度锥削阵结构与FDA概念结合，得到如图9所示的发射方向图。与图7和图8相比，本文方法在目标点处形成的主波束宽度在距离维和角度维均更窄，辐射能量更为集中，分辨率更高，具有更好的抗干扰能力。

仿真2： 密度锥削阵间距递增因子a的取值对方向图的影响。

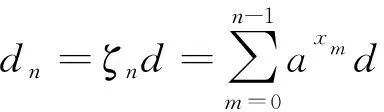
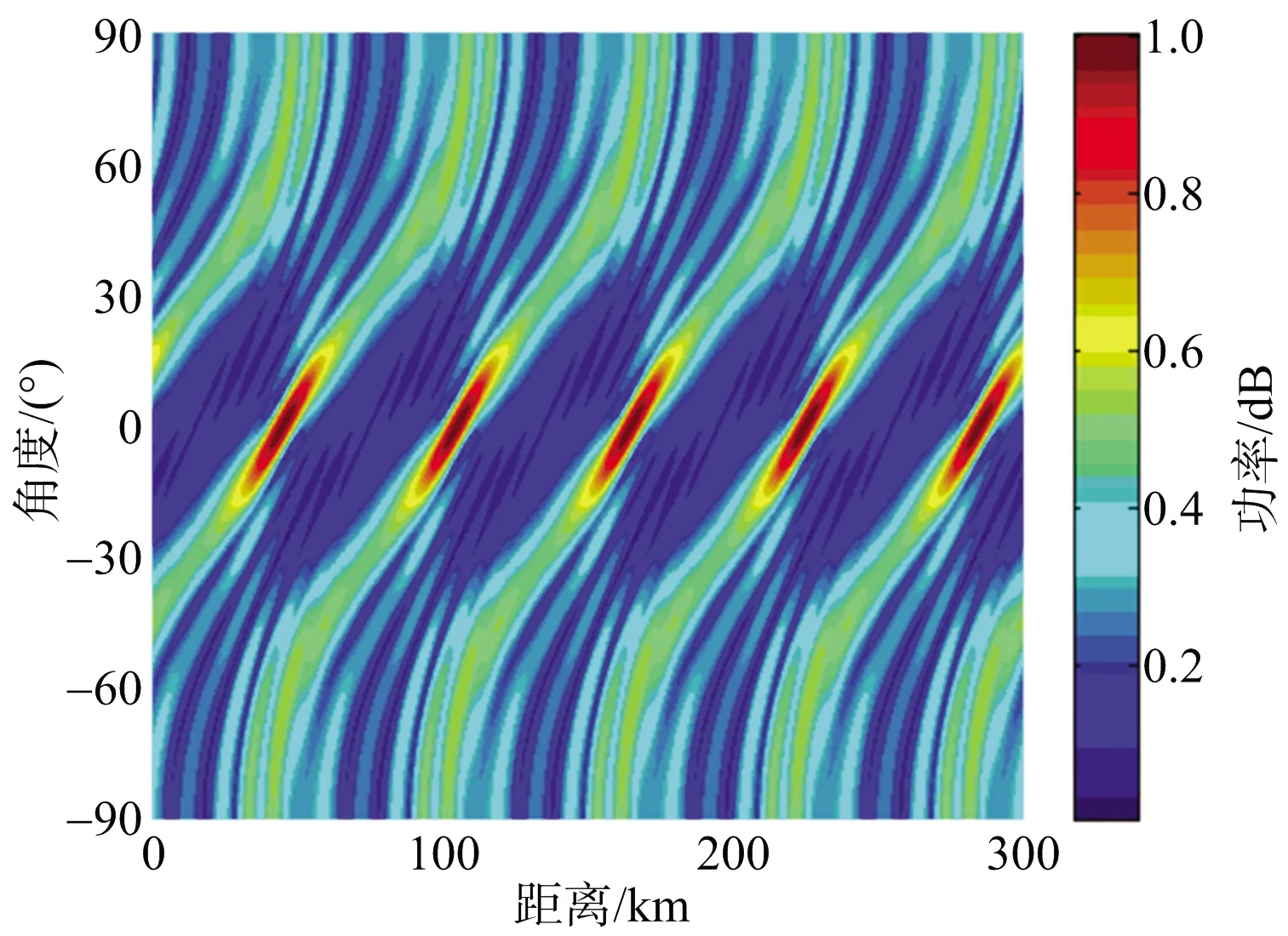
图10 密度锥削阵FDA发射方向图(a=0.1)

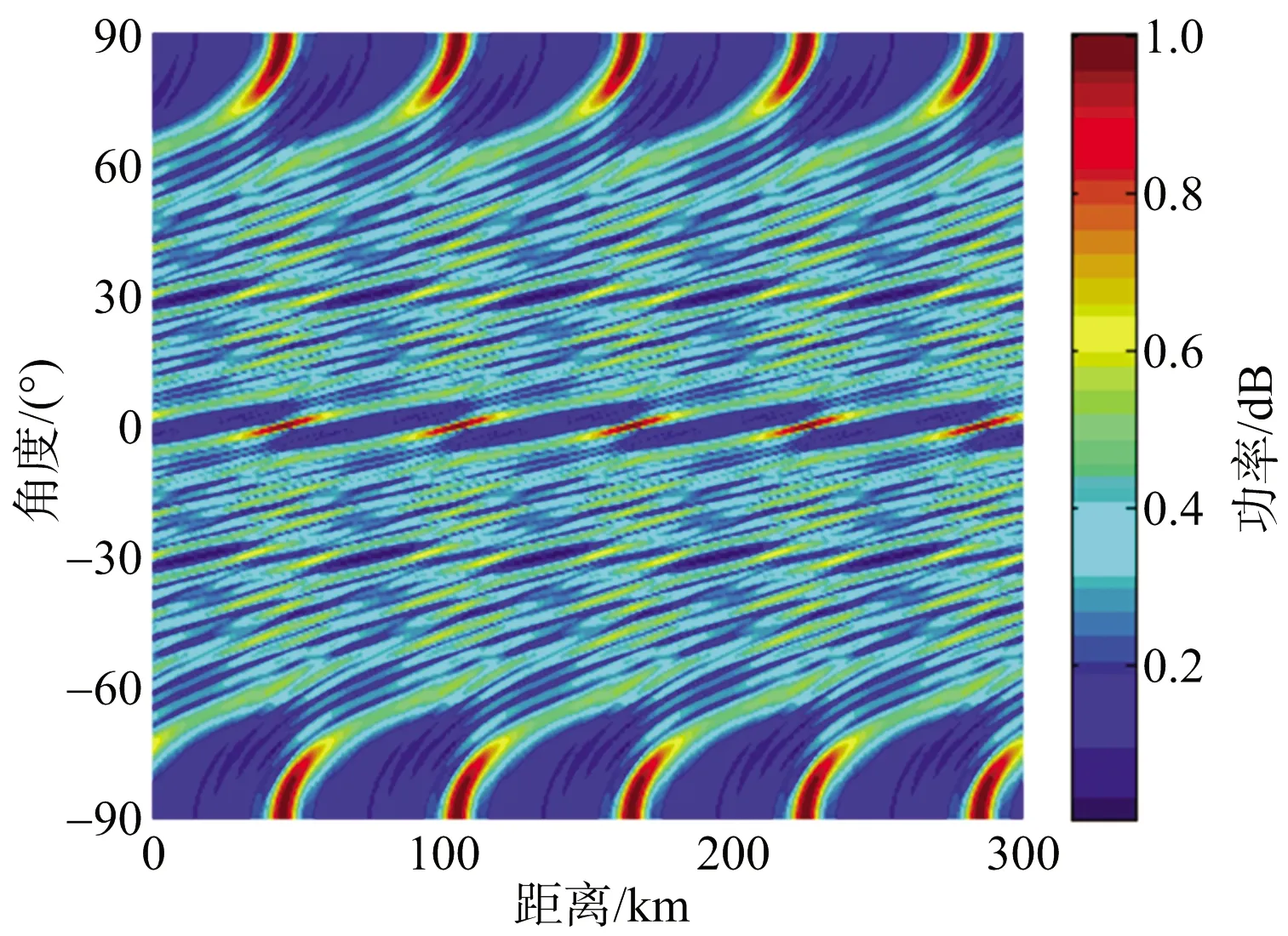
图11 密度锥削阵FDA发射方向图(a=4)

仿真3： 密度锥削阵中xm的函数形式对方向图的影响。

图12所示为xm=sin(m)时密度锥削阵FDA的发射方向图，图13所示为xm=log(m+1)时密度锥削阵FDA的发射方向图，图14所示为xm=m2时密度锥削阵FDA的发射方向图。由图12～图14可知，xm函数形式会影响方向图的主波束形状，对数和正弦函数形式的波束都与ULFDA的波束形状相似，但发射能量更为集中。当xm=m2方向图会出现主瓣畸变的问题。由图12～图14可知，当xm采用正弦、对数、指数函数时，密度锥削阵FDA并未有效消除方向图固有的距离-角度耦合问题。

图12 密度锥削阵FDA发射方向图(xm=sin(m))

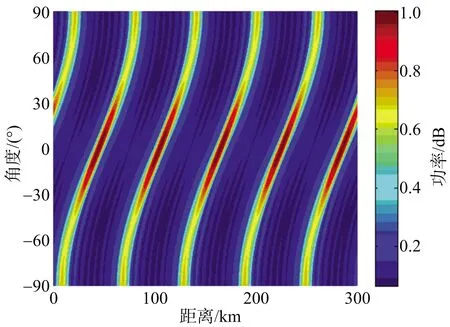
图13 密度锥削阵FDA发射方向图(xm=log(m+1))

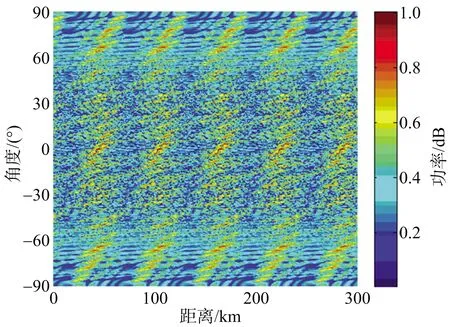
图14 密度锥削阵FDA发射方向图(xm=m2)

仿真4： 密度锥削阵中频控函数Δfn对方向图的影响。

由文献[10]的分析可知正弦频控函数具有较好的阵列性能，将Δfn=sin(n)代入密度锥削阵FDA结构中得到如图15所示的阵列方向图。由图15可知，采用正弦非线性频控函数的密度锥削阵FDA可在目标位置处形成点状的波束指向，但方向图中的距离-角度耦合问题仍需在后续的研究中进一步消除。ULFDA的波束图中存在着固有的距离-角度耦合问题，非线性频控函数的使用是消除这一耦合的重要手段。由仿真3和仿真4可知，如何有效消除密度锥削阵FDA发射方向图中的距离-角度耦合问题是下一步研究的重点。

图15 密度锥削阵FDA发射方向图(Δfn=sin(n))

4 结束语

FDA雷达能够产生距离-角度-时间相关波束，在雷达目标的距离-方位角联合估计、射频隐身以及前视探测与成像等领域都有广阔的应用前景。本文仿真分析了密度锥削阵FDA结构发射方向图与PA、ULFDA和log-FDA相比的性能优势，以及密度锥削阵间距递增因子、非线性频控函数设计对方向图的性能影响。而为后续FDA雷达一维阵列结构设计的进一步研究奠定了基础。