空间步进频雷达多参数联合稀疏估计方法

贾远航， 贺 顺， 杨志伟， 罗彩祯

(1. 西安科技大学通信与信息工程学院， 陕西西安 710054;2. 西安电子科技大学雷达信号处理国家重点实验室， 陕西西安 710071)

0 引言

空间步进频雷达系统采用多个天线发射相互正交的步进频信号，实现全空域覆盖，接收端采用多天线同时接收，每个接收天线接收来自所有发射天线发射的不同频率信号，将各频点信号分离后进行子带拼接可以得到大带宽信号[1]，同时多天线产生的虚拟孔径增大了阵列孔径。因此，相对于传统的时间步进频雷达，提高了空间分辨率和时间利用率。

传统的空间步进频二维目标定位方法是先对接收导向进行波束形成得到接收角度，然后再对发射孔径进行发射脉冲综合，同时实现脉冲压缩和发射孔径综合，得到距离-角度二维估计信息[2]；由于脉冲综合实际是在补偿发射角度相位的同时利用IFFT实现步进频脉冲压缩，所以传统方法受实际带宽和阵列孔径的约束，空间分辨率较低，想要获得高精度参数估计，需要采用超分辨算法。文献[3]采用MUSIC算法得到距离超分辨估计，相较于IFFT分辨率更高，旁瓣更低。由于空间步进频接收信号是距离-角度耦合的，因此，存在量化误差，距离和角度估计偏差较大，为了提高距离和角度的分辨率，文献[4-5]采用2D-MUSIC算法实现距离-角度二维超分辨估计，在一定程度上消除了由于距离和角度耦合产生的估计偏差，但在少快拍或者相干目标情况下MUSIC算法性能恶化严重[6]。稀疏恢复在少快拍和相干目标情况下具有很好的目标参数估计性能[7-10]。文献[11]利用稀疏迭代自适应算法(Iterative Adaptive Approach，IAA)实现了距离-角度的二维图像估计，在少快拍甚至单快拍情况下仍然具有较好的性能。然而IAA在二维功率谱估计中主瓣较宽，且在主瓣附近存在较多的虚假峰值，针对这一问题，文献[12]提出了稀疏迭代的加权q范数最小化(lq-Sparse Iterative Minimum，lq-SIM)方法，利用q范数提高功率的稀疏性，使得主瓣宽度减小，分辨率增加，同时消除了虚假峰值。然而IAA和lq-SIM只具有局部收敛性，且均为单快拍数据优化形式，扩展到多快拍时相对复杂[13-14]，导致时间复杂度增加，收敛速度较慢。基于协方差拟合的稀疏迭代(Sparse Iterative Covariance-based，SPICE)方法[15]，将接收数据转换成协方差矩阵，得到协方差拟合的加权最小二乘算法，在多快拍或少快拍数据中均适用，并且具有全局收敛性。然而，SPICE并不能很好地得到目标的能量测量值，在相干目标情况下估计偏差较大[16]。迭代稀疏渐进最小方差(Sparse Asymptotic Minimum Variance，SAMV)准则[17]能很好地解决SPICE能量估计不准确的问题，具有较高的估计精度，对少快拍和相干信号具有很好的鲁棒性，但在低信噪比情况下参数估计的稳定性较差，在真实目标周围存在较多虚假峰值，导致估计偏差增大。

为解决上述问题，提高空间步进频雷达在少快拍和低信噪比情况下距离-角度二维估计精度，提出了一种改进的空间步进频雷达距离-角度二维联合稀疏估计方法。仿真结果表明，本文方法能够有效提高在少快拍和低信噪比情况下目标距离-角度二维估计精度；并且在相干目标情况下仍具有较好的估计性能。

1 空间步进频信号模型

考虑远场窄带的空间步进频雷达，采用N个发射阵元和M个接收阵元，假设收发天线为全向性的均匀线阵，发射与接收阵元的间距等于半波长，即dt=dr=d=c/(2f0)，c为电磁波传播速度，f0为参考频率。第n个阵元发射的信号形式如下：

sn(t)=rect(t)ej2πfnt,0≤t≤Te,n=1,…,N

(1)

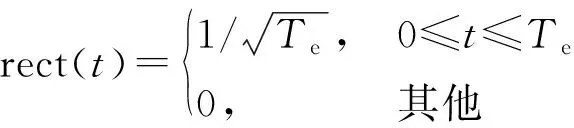
exp(-j2πfjτ0j)=0

(2)

假设以第一个发射阵元和接收阵元作为参考阵元，对于空间中在距离rp和角度θp处的目标在第m个接收阵元的接收信号为

exp[j2πfn(t-τp,n,m)]

(3)

式中，τp,n,m表示目标的延时，主要包括目标的双程延时、发射阵元延时差和接收阵元延时差，第n个发射阵元经过目标反射后到第m个接收阵元对应的延时相位为

φp,n,m=2πfnτp,n,m=2π[f0+(n-1)Δf]×

(4)

由于空间步进频发射相互正交的信号，在接收端经过预处理可以将信号进行频率分离，再将频率拼接形成大带宽的接收信号模型。第m个接收阵元的信号预处理流程如图1所示。

图1 第m个接收阵元的信号预处理流程

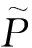
(5)

(6)

式中，上标Τ为转置处理，λ为参考频率的波长。将L个快拍的接收数据写成矩阵形式如下：

Y=Aα+ε

(7)

假设目标与目标和目标与噪声信号之间相互独立，则对应的接收信号的协方差矩阵为

R=E{YYH}=APAH+σI

(8)

(9)

2 基于2D-lq-SAMV的距离-角度二维超分辨估计

SAMV是基于渐进最小化方差(Asymptotic Minimum Variance，AMV)准则[18]得到的稀疏迭代算法。SAMV算法的参数估计性能与最大似然估计相同，可以实现高精度的目标参数估计；但在低信噪比时SAMV的稳定性较差，导致低信噪比估计偏差较大。为了增强SAMV在低信噪比情况下的稳定性，本文提出了一种改进的基于加权lq-范数的二维稀疏渐进最小方差(2D-lq-SAMV)方法，实现距离-角度二维估计。该方法的最优化目标函数形式为

(10)

试验在眉山中车紧固件科技有限公司完成。转向架制动杠杆1、2铆接位置预先铆接完成，试验的检测对象为转向架制动杠杆的4个铆接位置(3、4、5、6号位置)的铆接状态。

(11)

由于ri与pi无关，对式(11)求关于pi的偏导，可以得到

(12)

将ri的变换式代入式(12)中，利用下面两个矩阵的性质和Capon谱估计公式对上式进行化简：

(13)

(14)

则第i个网格点在第j+1次迭代的功率值为

(15)

(16)

算法的具体步骤如表1所示。

表1 2D-lq-SAMV算法步骤

(17)

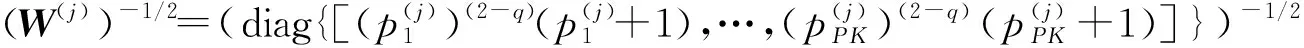
3 仿真实验分析

为了验证本文所提方法的有效性，下面以空间步进频雷达为例进行仿真实验。发射和接收阵元个数为N=M=7，发射和接收阵元的间距为dt=dr=d=λ/2，λ为初始频率f0的波长，f0=10 GHz，Δf=500 kHz，等效的信号带宽为Bw=NΔf=3.5 MHz，对应的距离分辨率为Δr=c/(2Bw)≈42.86 m。假设远场存在4个点目标位于同一距离窗内，分别是(r1,θ1)=(346 m,-14°)，(r2,θ2)=(370 m,10°)，(r3,θ3)=(450 m,-8°)，(r4,θ4)=(510 m,18°)，各目标功率分别为8，10，8和5 dB，初始的参考距离为300 m，快拍数L=10，目标3与目标4是相干的，其他均为非相干目标。将本文算法2D-lq-SAMV与2D-SAMV算法进行两次对比，信噪比分别为SNR=5 dB和SNR=20 dB，范数q=0.6，如图2、图3为20次蒙特卡洛实验结果。红色虚线为真实目标所在位置。从图中可以看出，在高信噪比情况下，无论是本文方法还是SAMV都具有较高的估计精度。在低信噪比情况下，相比于SAMV，本文方法的稀疏性更好，稳定性更高，功率谱估计的准确性更高，没有虚假峰值，而SAMV在主峰附近存在较多的虚假峰值，估计偏差较大。从整体可以看出，本文所提方法在低信噪比情况下具有很好的鲁棒性，并且对相干目标仍具有较高的估计性能。

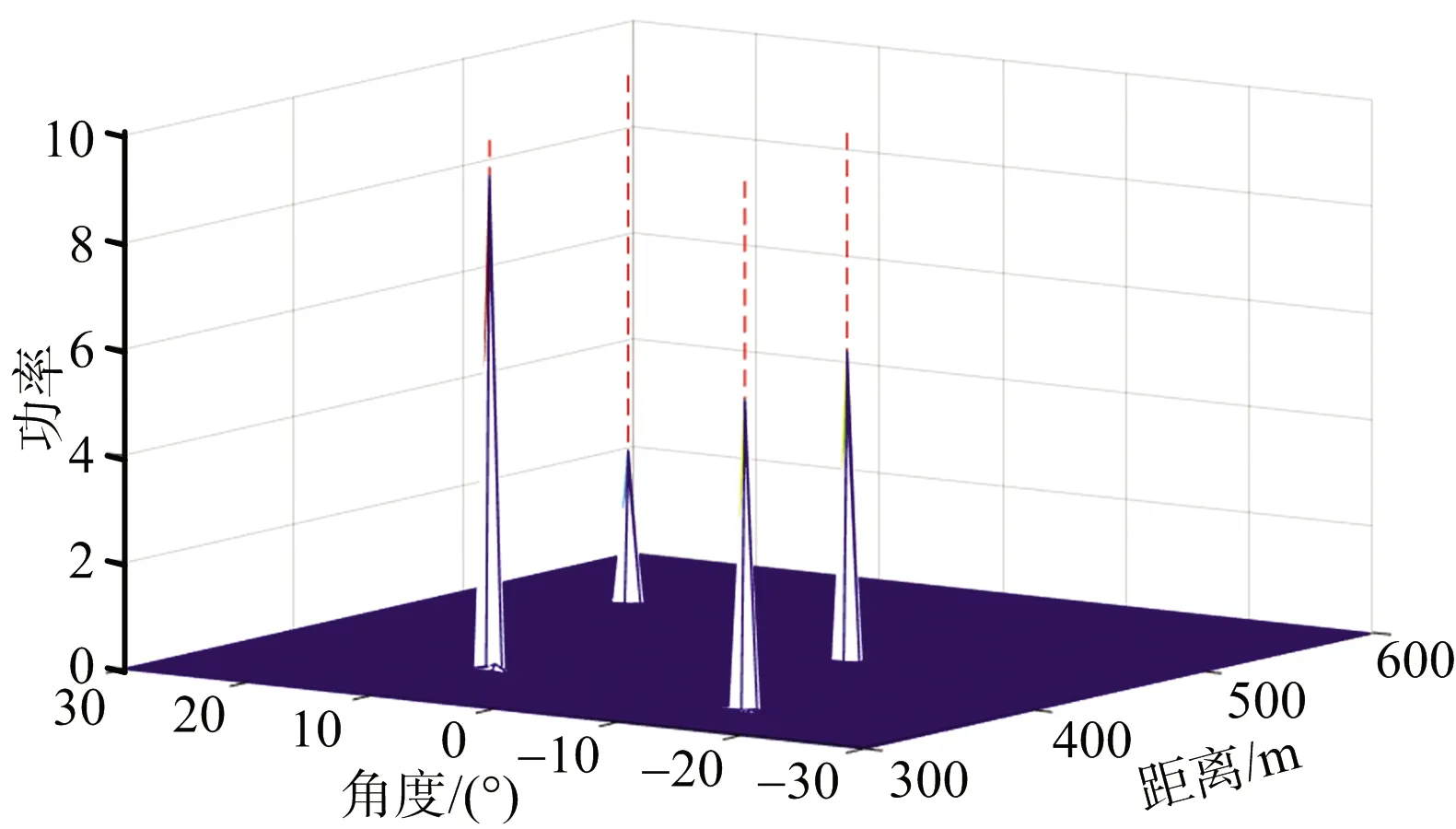
(a) 本文所提方法lq-SAMV

(b) 原文方法SAMV图2 高信噪比SNR=20 dB

(a) 本文所提方法lq-SAMV

(b) 原文方法SAMV图3 低信噪比SNR=5 dB

为了进一步验证算法性能，下面将本文方法与2D-Beamforming、2D-MUSIC、2D-lq-SIM和2D-SAMV算法进行对比，给出在不同信噪比下距离、角度均方根误差(Root Mean-Square Errors，RMSE)和平均迭代时间曲线。考虑空间远场中两个目标，分别位于(r1,θ1)=(338 m,3.1°)，(r2,θ2)=(365.8 m,18°)，目标的功率为8 dB和10 dB，快拍数L=10，发射和接收阵元N=M=8；距离划分区间为[300∶ 1∶ 400]m，角度区间为[-10°∶ 1°∶ 30°]，范数q=0.7。图4是在非相干目标情况下的500次蒙特卡洛实验结果，从图4可以看出，由于2D-Beamforming分辨率受孔径和带宽限制，主瓣宽度较宽，导致两个临近目标无法分辨。 2D-MUSIC由于快拍数较少，信号子空间与噪声子空间的正交性差，当信噪比较低时性能恶化严重，从图中可以看出，当SNR大于13 dB时估计性能才较好。相比于2D-SAMV和2D-lq-SIM，所提的2D-lq-SAMV方法在低信噪比时具有更小的均方根误差，而2D-lq-SIM在SNR小于8 dB时无法实现目标参数估计。信噪比大于15 dB时，2D-lq-SIM距离均方根误差略小于2D-lq-SAMV，从图4(a)距离均方根误差曲线可以计算出2D-lq-SIM与2D-lq-SAMV距离均方根误差平均相差0.016 m；从图4(b)可以看出在信噪比大于15 dB时角度均方根误差相同；所以，当SNR大于15 dB时，2D-lq-SIM、2D-SAMV和2D-lq-SAMV算法性能相似。图5是在相干目标情况下的500次蒙特卡洛实验结果，可以看出在相干目标情况下2D-Beamforming和2D-MUSIC均无法实现目标的参数估计；然而，本文算法2D-lq-SAMV在相干目标情况下仍具有较好的估计性能。从图6可以看出，无论对于非相干目标还是相干目标，所提的2D-lq-SAMV方法比2D-lq-SIM方法收敛速度都要快。综合所有仿真实验结果，本文所提方法性能更好。

(a) 距离均方根误差曲线

(b) 角度均方根误差曲线图4 非相干目标在不同SNR下的RMSE曲线

(a) 距离均方根误差曲线

(b) 角度均方根误差曲线图5 相干目标在不同SNR下的RMSE曲线

(a) 非相干目标的平均迭代时间

(b) 相干目标的平均迭代时间图6 不同SNR下的平均迭代时间曲线

4 结束语

本文利用空间步进频雷达回波特性，在接收端得到距离-角度联合的等效接收信号模型，针对稀疏渐进最小方差准则存在的问题，提出一种改进的基于加权lq-范数的稀疏渐进最小化方差方法，并利用2D-lq-SAMV得到空间步进频雷达距离-角度二维功率谱估计。通过仿真实验表明，2D-lq-SAMV对于少快拍和相干目标情况仍具有较好的鲁棒性；在少快拍时，相比于单快拍数据优化形式的2D-lq-SIM收敛速度更快。与2D-SAMV算法相比，所提的2D-lq-SAMV算法的鲁棒性更好，在空间步进频距离-角度二维估计中精度更高。