基于K-SVD的星载GPS观测数据压缩方法

刘迎娜，赵里恒，李宏刚，董娟娟，李伟超

(航天恒星科技有限公司，北京 100095)

0 引言

随着卫星对地观测技术的发展，低轨空间飞行器已应用于资源遥感、大气探测、重力场精化、地磁探测和海洋动力环境研究等领域，并且低轨飞行器大部分应用领域，对卫星轨道精度有较高要求，例如海洋测高卫星TOPEX要求轨道径向精度优于 5cm[Melbourne,1994]等[1-2]，促使低轨空间飞行器精密定轨技术[3]得到快速发展。精密定轨技术需空间飞行器事先对星载GPS导航系统的观测数据进行存储，再分时下传到测控站，考虑到星载GPS观测数据存在数据量大的特点，为星载固存[4]的存储资源增加负担，提出了GPS观测数据压缩处理的工程应用需求。

目前相关方面研究主要面向地面Rinex格式GPS观测数据的压缩[5-6]，根据数据中字符出现的冗余情况，对其进行熵编码实现数据压缩，为无损压缩方法，此类方法对文本文件压缩具有应用优势，但对于星上实时产生的二进制GPS观测数据时间序列，压缩效果不明显，且计算复杂度高，无法满足在轨使用。除无损压缩方法外，基于信号变换的有损压缩方法在声波、地震时间序列以及图像等应用研究中取得了显著成果，该方法主要利用信号处理中存在某些频率成分不敏感特征，允许压缩过程中损失一定的信息，虽然不能完全恢复原始数据，但所损失的部分特征需不影响信号处理应用，从而达到高的数据压缩比(压缩前数据量与压缩后数据量的比值)，较为常用的方法有傅里叶变换、DCT变换以及小波变换等。星载GPS观测数据属于精密测量信息，在高压缩比条件下使用上述方法，将大量丢失GPS观测数据的内部结构信息，无法满精密定轨处理要求。

信号稀疏表示理论在信号处理应用中是一个非常引人关注的研究领域，其目的就是在给定的完备字典中用尽可能少的原子来表示信号，获得信号更为简洁的表示方式，利用信号的稀疏性，可实现信号压缩应用，并成功应用于图像[7-8]、地震[9]等数据压缩。

本文对稀疏表示理论在GPS观测数据的压缩应用进行研究，提出了基于K-SVD的GPS观测数据压缩方法。利用一个通过训练样本训练获得的K-SVD压缩字典，对GPS观测数据时间序列进行稀疏表示，并对表示系数中非零元素位置和数值进行存储和传输，从而实现GPS观测数据压缩。

1 稀疏表示理论

通常，有限维空间RN中的一维离散信号y可以线性表示为：

y=Dξ

(1)

稀疏表示问题可分为稀疏编码和字典学习两部分。给定信号y和字典D，稀疏编码就是寻找稀疏解ξ的过程，它可以表示为如式(2)所示的优化问题：

(2)

式(2)为l0范数最小化问题，通常采用贪心算法近似求解该问题，如正交匹配追踪[10](Orthogonal Matching Pursuit,OMP)。与稀疏编码不同，字典学习用于估计基函数字典D。给定一个包含P个信号的训练样本集合Y={yi|yi∈RN},1≤i≤P，字典可以通过求解公式(3)的优化问题获得。

(3)

其中：‖dk‖2=1，1≤k≤K；ξi为信号yi在字典D中线性表示的系数；S为ξi中非0元素的个数。

2 GPS观测数据压缩方法

星载GPS导航系统通过接收处理GPS L1、L2双频点导航信号[11-12]，计算获取表征GPS导航接收机与GPS星座相对位置关系的伪距、载波相位等测量量，统称为GPS观测数据，如图1所示。

图1 低轨卫星与GPS星座空间位置关系图

那么GPS观测数据组成的时间序列为描述GPS导航接收机与GPS星座之间相对运动关系的离散采样信号，具体实例见图2所示。

图2 对GPS_ 25号星的伪距观测数据时间序列

不同时间段对同一颗GPS星号、相同时间段对不同GPS星号的观测数据时间序列的内部结构相似、且简单，存在信息冗余，能够通过稀疏表达方式，实现GPS观测数据时间序列压缩。

具体压缩流程如图3所示。

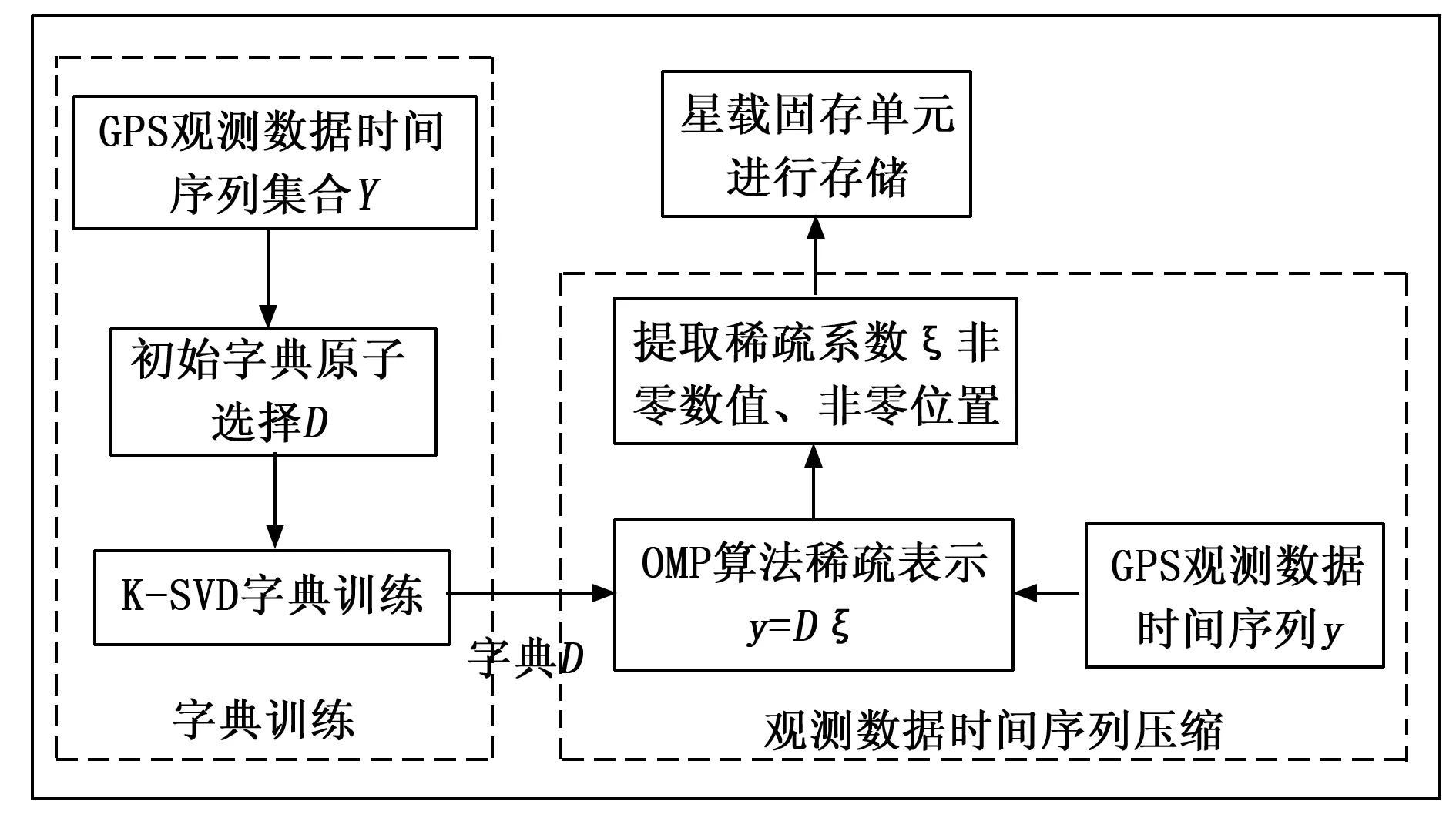
图3 GPS观测数据时间序列压缩方法框图

2.1 训练样本选取

将GPS观测数据时间序列裁剪成短时长时间序列集Y={y1,y2,...,ym,...,yP}∈RN×P，作为字典学习样本集合，其中ym={a1,a2,...,ai,...,aN}T∈RN×1，ai表示GPS观测数据时间序列ym中第i个观测点，具体裁剪实例如图4～5所示。

图4 时长为1 800 s的伪距观测数据时间序列变化曲线

图5 伪距组成的时间序列集合(N=200 s)

2.2 字典D初始化方法

主成分分析[13](PCA，principal component analysis)是基于变量协方差矩阵原理完成对信号的逻辑处理和特征提取的科学方法，同时也是一种最基本的数据降维方法，被广泛用于图像去燥[14]、图像分类[15]等，同时也被用于数据处理中参数初始化操作，提高优化处理收敛速度[16]。本文引用PCA方法初始化公式(3)中的矩阵D，将缩短最优字典D的求解时间。

GPS观测数据时间序列样本集合Y={y1,y2,...,yP}∈RN×P为数据集合，通过优化求解公式(4)目标方程获取主成分矩阵U=WTY。

maxWTYYTWs.t.WWT=1

(4)

需计算数据矩阵Y的协方差矩阵，对计算带来困难，引入了奇异值分解(SVD,singular value decomposition)方法，即Y=UΣV。其中，V等价于PCA算法中W投影矩阵；U即为主成分矩阵；Σ为对角阵，表示Y投影到新坐标系下的权值系数。

2.3 字典学习方法

K-SVD[17]是 K-均值聚类(K-means)的一般形式，通过字典更新、稀疏编码交替应用，实现对字典的自适应调整。稀疏编码过程，使用OMP编码方法；字典更新过程使用奇异值分解(SVD)。

参数初始化：给定GPS观测数据组成的时间序列数据集合Y={y1,y2,...,ym,...,yP}∈RN×P，对其进行主成分分析获取主成分矩阵U，作为字典D(0)∈RN×K，最大迭代次数为Iter，稀疏编码中非零个数惩罚项为S。

1)稀疏编码阶段，使用OMP对目标函数公式(2)进行稀疏分解，得到稀疏系数矩阵ξ={ξi},i=1,2,...,P。

2)字典更新阶段，固定稀疏系数矩阵ξ，逐列更新字典D中的原子。

(1)假定当前正在更新的字典原子为dk，记Ik={i|ξi(k)≠0,1≤i≤P}，其中ξi(k)为ξi中的第k个元素，Ik表示全部训练样本中用到原子dk的索引集；

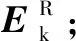
(4)计算K次，对D所有原子更新一遍，获得D(n+1)。

网络课程资源建设和完善，不仅会为成人高等教育的学生提供优质的学习资源，还能够补齐学校校外、课外学习资源的短板。它能够全面覆盖学生的自由学习时间，也能为广大学生提供高质量的教育和学习资源服务，为高校节约办学成本。网络课程资源必将以其便捷性、丰富性、自主性、个性化的服务，为广大学生的专业学习和素质拓展提供更加坚实的基础和有力的保障。

3)终止条件判断阶段，令n=n+1，判断是否满足n>Iter，若满足，停止迭代，否则，继续执行1)～3)。

2.4 GPS观测数据压缩

导航接收机积累N时长的GPS观测数据时间序列后，使用K-SVD对其进行稀疏编码，并将获取表示系数中的非零数值、非零位置存储到星上固存单元，达到GPS观测数据压缩目的，数据压缩比近似为N与稀疏度S的比值。

3 实验验证

通过仿真软件获取理论GPS观测数据时间序列，生成训练样本集合，使用文中提到的方法训练获得K-SVD字典。通过地面仿真，获取不同轨道高度场景下双频GPS导航接收机生成的压缩前/后观测数据，对观测数据重构精度进行分析，并对比GPS观测数据压缩前后的数据质量、精密定轨精度；同时引入实际在轨GPS观测数据，对其进行压缩重构后精密定轨精度进行分析，检验方法的有效性。

3.1 压缩字典获取

3.1.1 参数设置

使用SimGEN软件仿真获取650 km轨道高度的无测量噪声的星载GPS观测数据，仿真软件界面、软件参数设置详见表1所示。

表1 SimGEN软件参数设置

将GPS观测数据时间序列长度N设置为30 s；稀疏度S设置为4；字典迭代次数Iter设置为800。那么数据压缩比即为ρ≈N/S≈7.0。

3.1.2 字典训练收敛性分析

对K-SVD压缩字典进行迭代更新，并按照公式(5)评估字典优化过程收敛情况。

(5)

通过误差收敛曲线分析可知，使用PCA初始化压缩字典后的第一次字典更新完成获得的字典已具有高精度稀疏稀疏表达训练样本的能力，经过多次调整，最终在第600次迭代更新后完成收敛，获得最优K-SVD压缩字典，如图6所示。

图6 K-SVD学习过程误差收敛曲线

3.1.3 字典结构分析

对K-SVD字典中的原子分别进行分析可知，训练获取的K-SVD字典为表征信号运动规律(一次、二次、三次曲线变化规律)的基函数集合，与GPS观测数据组成的时序信号内在结构信息一致，具体基函数变化规律如图7所示。

图7 字典中基函数变化曲线图

随机选择100个测试样本，按照不同稀疏度约束，使用K-SVD字典对其进行稀疏分解，按照公式(5)计算稀疏重构误差，具体误差值如表2所示。

表2 重构误差统计表

由表可知，当稀疏度>4时，稀疏表达精度无明显提升，因此GPS观测数据时序信号在上述训练获取的K-SVD字典中是稀疏的，且稀疏度为4。

稀疏度固定后，相应压缩比将固定。实际工程应用中，双频GPS接收机每秒产生560字节的GPS观测数据，使用K-SVD字典稀疏表达方式，可对连续观测24小时共48.38兆字节观测数据压缩到6.912兆字节，具有显著的压缩效果。

3.2 地面设备仿真验证

使用双频GPS导航系统、思博伦GPS信号模拟源、上述训练获取的K-SVD压缩字典以及4种不同轨道高度的轨道参数等，开展地面仿真测试。

具体仿真轨道参数如表4所示。

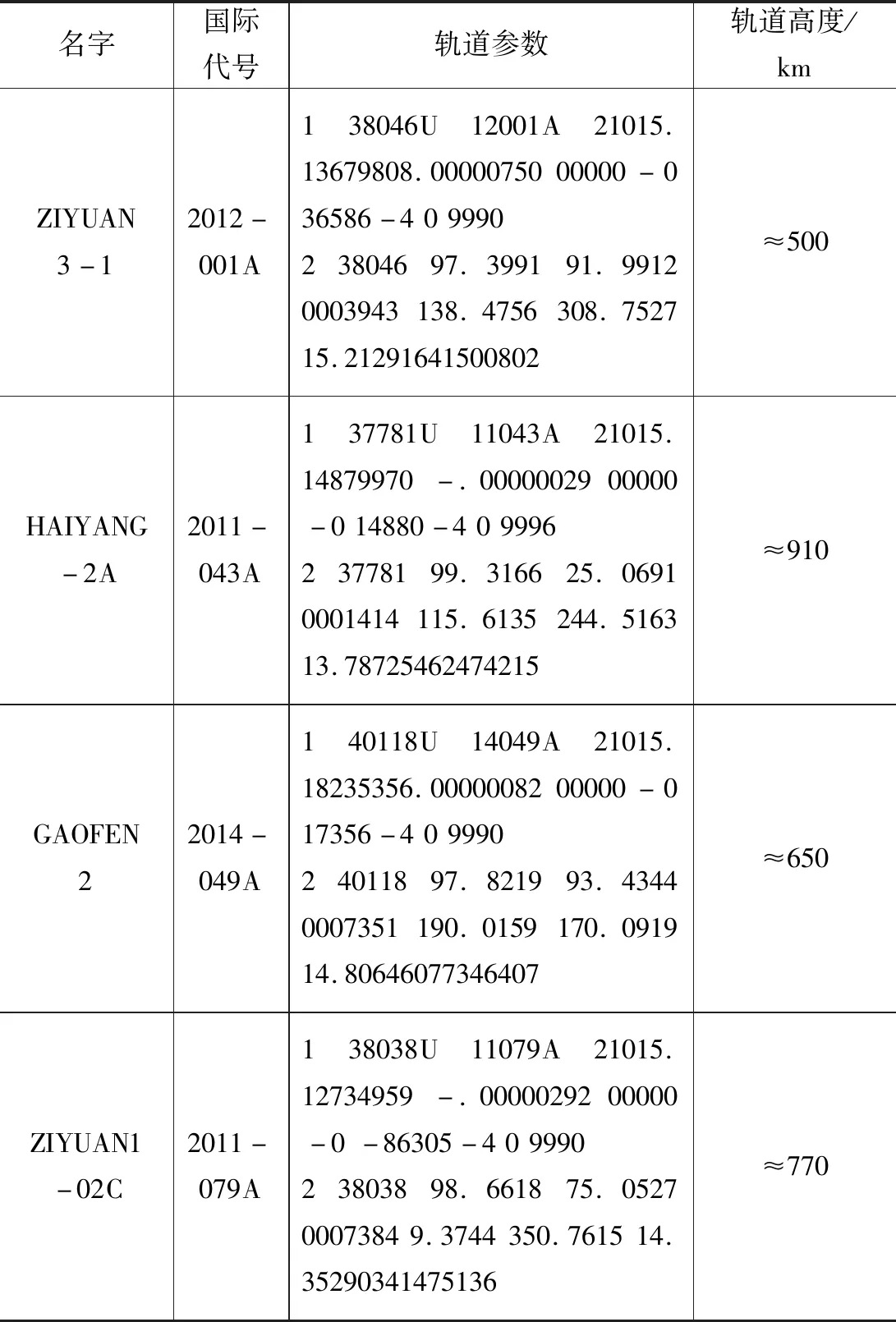
表4 仿真轨道信息

3.2.1 重构精度分析

考虑到信号处理射频电路中带电粒子的热运动形成热噪声等，双频GPS接收机实际观测的GPS数据中将存在噪声，使用K-SVD字典对其进行压缩重构，重构误差将大于字典学习误差收敛值，但重构误差需控制在<5 cm范围内，才可满足厘米级精密定轨应用需求。

对实验获取的L1、L2载波相位测量数据重构精度进行分析，使用相同的K-SVD压缩字典对不同轨道高度GPS观测数据压缩后的重构误差均<5 cm，压缩重构后数据满足厘米级精密定轨要求，具体详见图8～11所示。

图8 ZIYUAN 3-1载波相位测量值压缩重构精度

图9 HAIYANG-2A载波相位测量值压缩重构精度

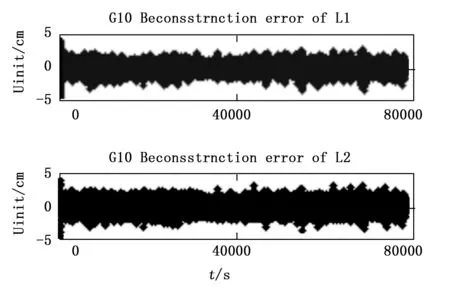
图10 GAOFEN 2载波相位测量值压缩重构精度

图11 ZIYUAN1-02C载波相位测量值压缩重构精度

3.2.2 观测数据质量分析

使用伪距相位差(code minus phase combination ，CC)组合法[18]评估压缩前后GPS观测数据的噪声水平，可知相同K-SVD字典压缩重构出的不同轨道高度GPS观测数据的噪声水平均明显低于压缩前GPS观测数据，说明K-SVD字典在GPS观测数据压缩应用中表现出显著的降噪效果，具体详见图12～15所示。

图12 ZIYUAN 3-1轨道GPS观测数据质量

3.2.3 精密定轨处理仿真

使用精密定轨技术[3]，对GPS观测数据进行精密定轨处理，并与理论轨道做差，获取X、Y、Z轴方向的轨道位置误差，误差曲线的标准差统计即为精密定轨精度。

通过精密定轨处理分析可知，使用K-SVD字典压缩后GPS观测数据的精密定轨精度优于压缩前观测数据，具体精密定轨精度比对如表5所示，精密定轨误差曲线图如图16～19所示。主要由于K-SVD字典的压缩方法，可通过降低GPS观测数据的噪声水平提升了观测数据的质量，从而提升了精密定轨精度。

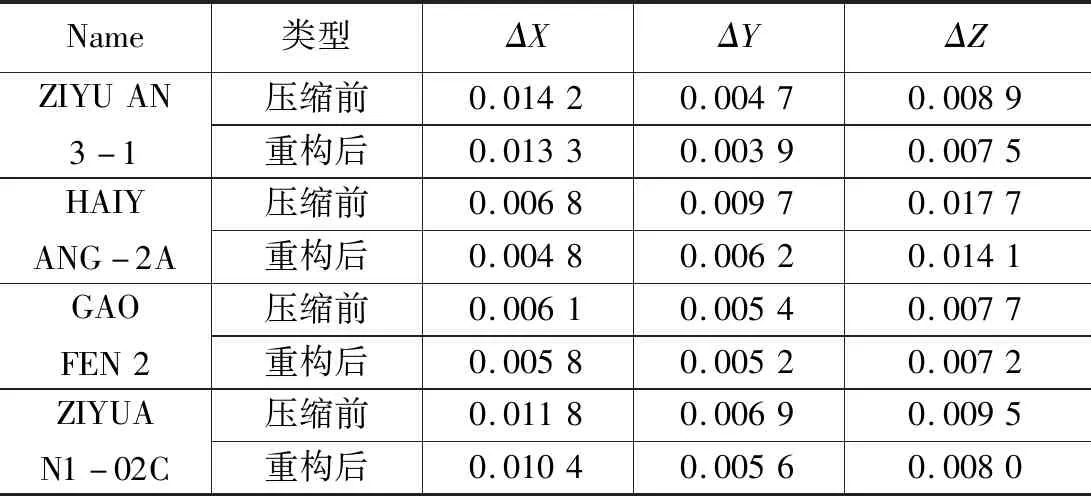
表5 精密定轨误差结果(轨道仿真) m

具体精密定轨精度曲线见图16～19所示。

图13 HAIYANG-2A轨道GPS观测数据质量

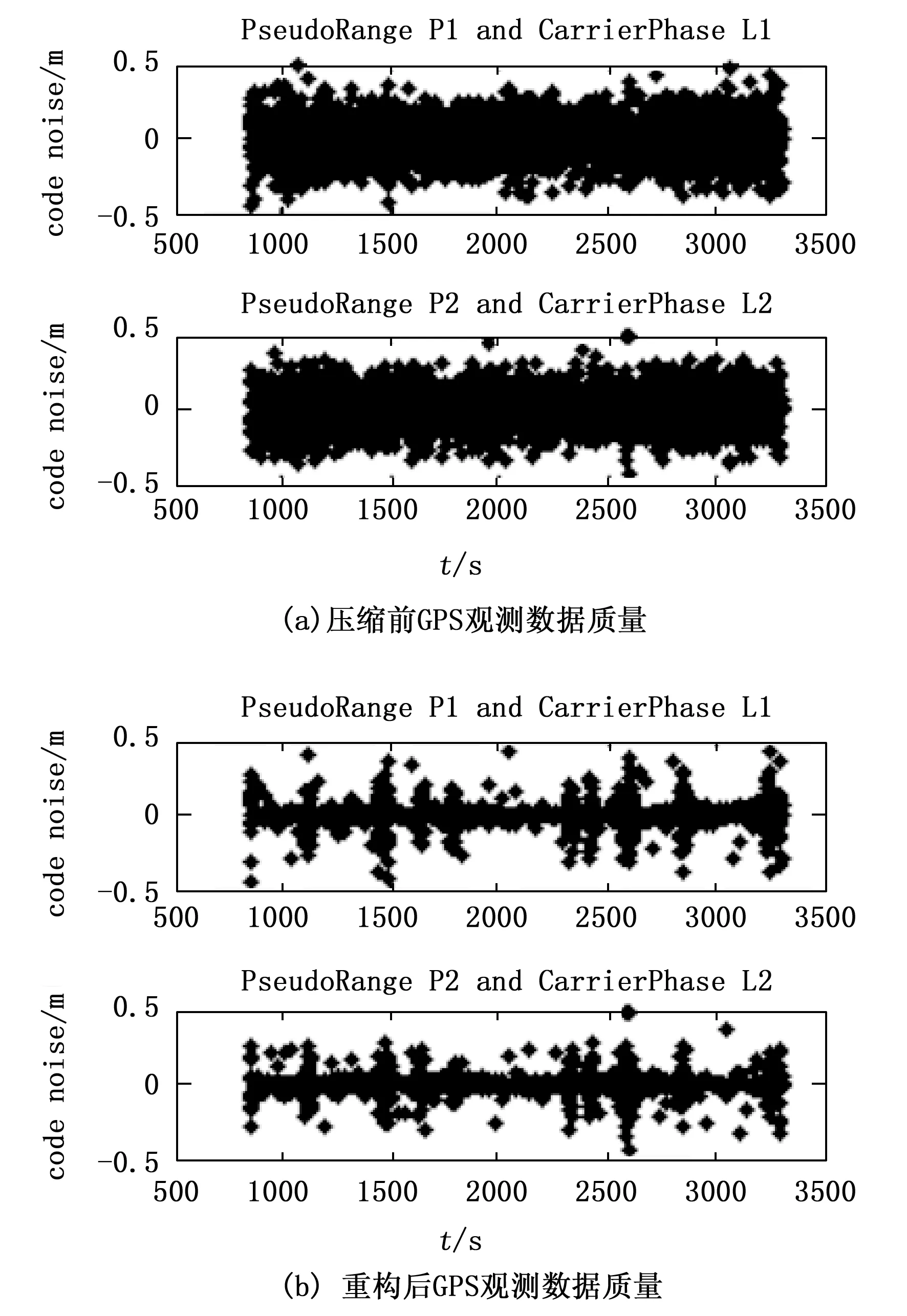
图14 GAOFEN 2轨道GPS观测数据质量

图15 ZIYUAN1-02C轨道GPS观测数据质量

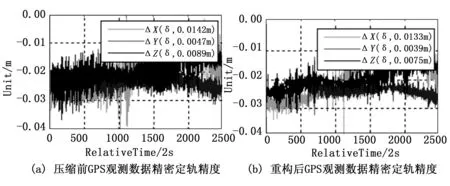
图16 ZIYUAN 3-1精密定轨精度

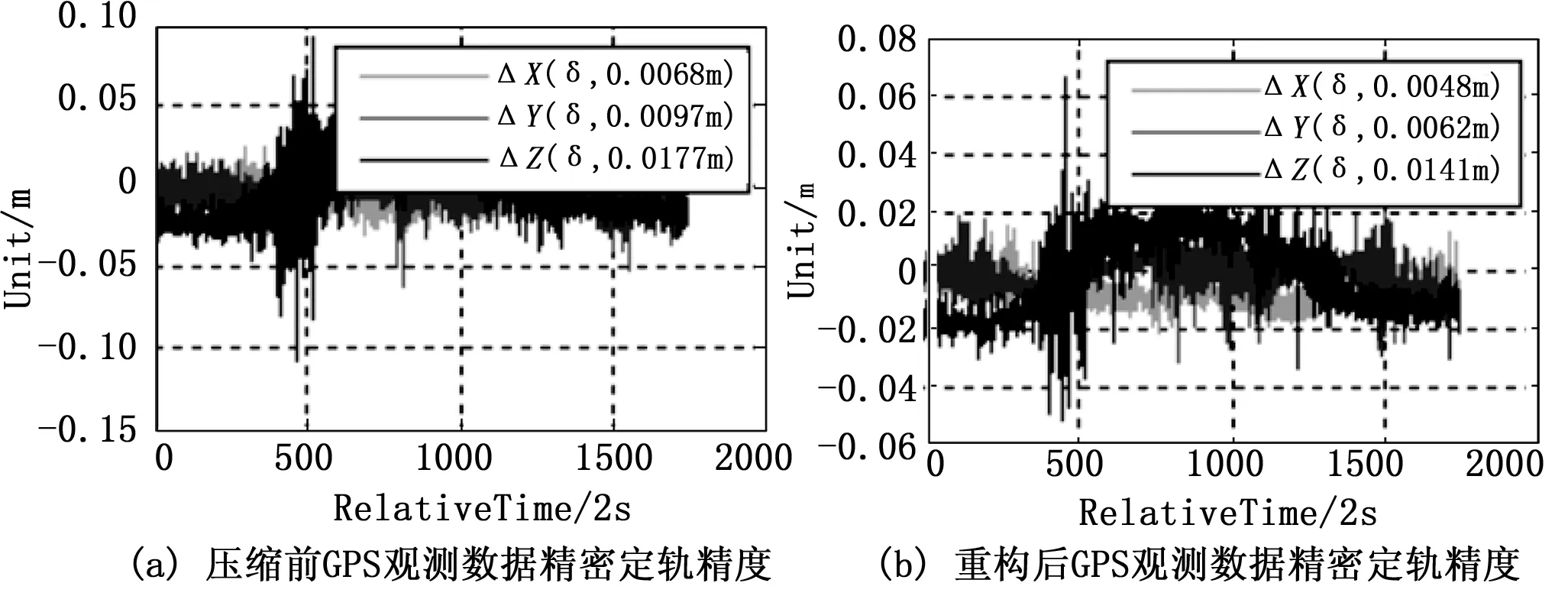
图17 HAIYANG-2A精密定轨精度

图18 GAOFEN 2精密定轨精度

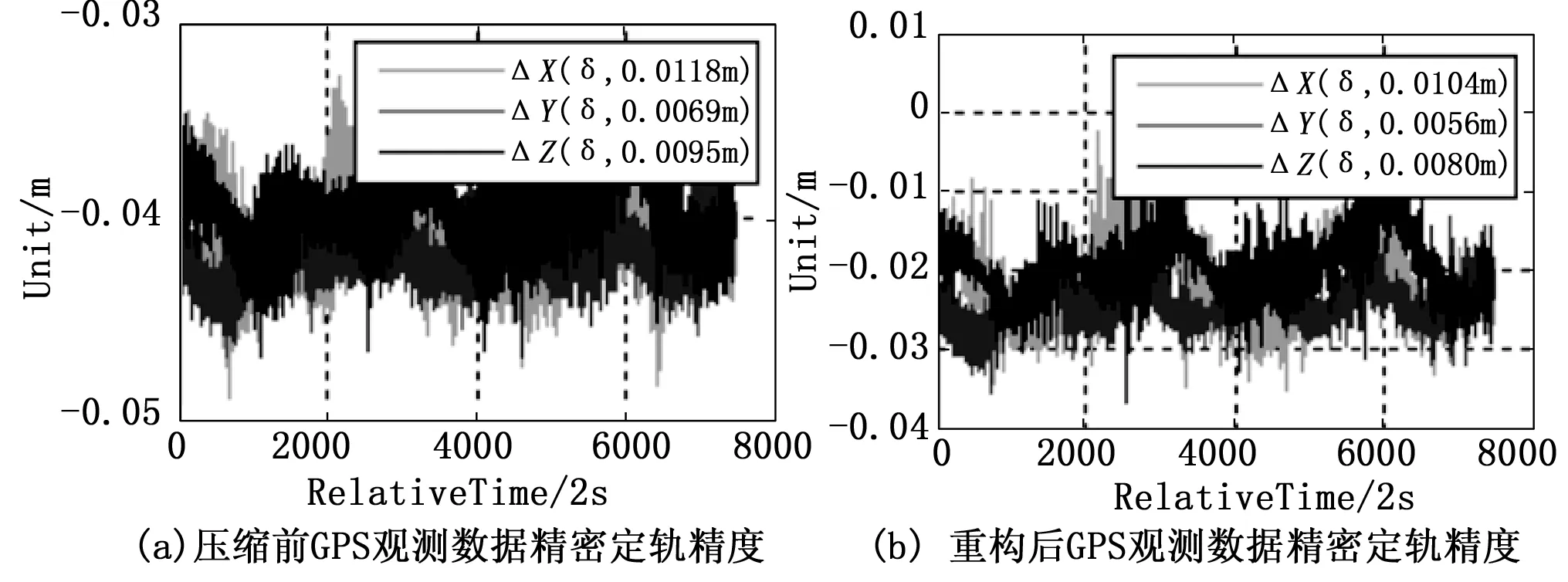
图19 ZIYUAN1-02C精密定轨精度

3.3 在轨实测GPS观测数据压缩效果验证分析

对资源一号02D卫星[19]下传到地面的GPS观测数据进行压缩重构试验，并对其进行精密定轨处理，计算压缩前后精密定轨数据差值可知，压缩后与压缩前相比X方向轨道位置相差0.014 6 m、Y方向轨道位置相差0.021 8 m、Z方向轨道位置相差0.011 2 m，具体详见图20所示。

图20 资源一号02D卫星在轨数据压缩后观测数据精密定轨精度

通过对在轨实测数据进行压缩前后精密定轨结果进行比对(误差≤0.022 m)，可说明压缩后观测数据重构精度高，使得压缩前后精密定轨结果相差较小。因此，文章提出的压缩方法可实际在轨应用。

4 结束语

通过实验仿真，文中提到的压缩方法能够对不同轨道高度的低轨卫星GPS观测数据进行高压缩比压缩，压缩比可达到7.0，并且能够降低观测数据的观测噪声，从而提升精密定轨精度。

由于星载GPS观测数据不仅可以应用于精密定轨，还有相对定位、大气层厚度反演[20]、土壤湿度反演等工程应用，而文中只针对精密定轨应用进行了实验仿真，后续将针对其他应用进行研究。