测量误差对输电线路交流电阻辨识的影响分析*

姚 浪 朱灵子 姚 瑶 赵 轩 曲晓蕾

（1.贵州电网有限责任公司 贵阳 550007）（2.南瑞集团有限公司（国网电力科学研究院有限公司）南京 211106）

1 引言

输电线路作为电能传输的载体和电力系统分析中的基础元件，输电线路交流电阻辨识的准确性对电力系统计算与分析有着重要的影响［1～2］。在进行电力系统分析时，如果所用的交流电阻参数不准确或者误差较大，会导致分析结果与实际情况偏离，严重影响电网运行人员对电网状态的判断和输电线路的调度利用。准确的线路参数是形成准确电网模型的前提，是对电网进行状态估计、潮流计算、网损分析和故障分析等电力系统计算的基础，因此研究输电线路交流电阻等参数辨识的准确性，对于提升电网的安全稳定运行意义重大［3～7］。

在实际的电力工程工作中，输电线路的交流电阻参数通常从设计手册等资料中查询获得，这些数值一般是根据输电线路的尺寸、材料、结构等物理参数，利用理论公式推算得到。这种理论计算方法一般会简化输电线路的电磁模型，忽略很多参数，另外随着输电线路运行时间增长，线路本身由于腐蚀、老化等原因也在发生变化，这种通过理论计算得到的交流电阻值不能真实反映输电线路的实际情况。最近几年，考虑从线路运行电气量的角度，通过对输电线路两端运行数据进行实时监测，采用在线方式获取输电线路的交流电阻等参数，成为工程实践中越来越常用的输电线路交流电阻辨识方法［8～11］。

通过线路两端实时电气量监测，进而计算线路交流电阻参数的方法，其计算的准确性与电气量的测量精度密切相关。在电气量测量回路中，互感器测量误差［12～13］、时间同步攻击［14～15］等各类原因，会导致实测电气量数据幅值、相角存在误差。在目前的研究中，主要集中在测量回路中单个环节测量误差的影响研究［13～17］，而较少测量回路整体测量误差对线路参数辨识的影响研究。

本文以输电线路π型等值电路为参数辨识模型，研究电气量测量回路整体测量误差对输电线路交流电阻参数在线辨识结果准确度的影响，为输电线路在线参数辨识的准确性和可用性提供评判参考。

2 输电线路电阻参数等值模型

根据电路理论，当输电线路长度较短时（＜100km），其电路模型可以用π型等值模型进行表示。集中参数π型等值电路，如图1所示，除了串联线路总阻抗外，还将线路总导纳分为两半，分别并联于线路两侧。

图1 π型集中参数等值模型

线路首末两端电压电流方程如下：

式中：

表示线路等值串联阻抗。

表示线路对地电纳，忽略电晕等影响，则不计对地电导，矩阵形式如下：

在实际测量中，分别在输电线路首端（M侧）和末端（N侧）配置测量装置，首末端的测量装置实时同步测量，获取线路两端的电气量，然后根据上述计算式（5）和式（6），对输电线路的交流电阻参数进行辨识计算。

3 测量误差的影响分析

输电线路两端的电气量数据是通过电压互感器、电流互感器测量而来，在数据测量中，由于互感器测量存在误差，会对输电线路的电阻参数辨识带来影响［18～21］。由输电线路的电阻参数等值模型可以看出，线路电阻参数的计算与线路两端的电压、电流相量密切相关。本文中通过灵敏度分析法对电气量测量误差的影响进行深度分析。

定义函数s与变量a自己的函数关系表示为

则把s相对变量a变化的灵敏度σ定义为

在本文中，所求的输电线路电阻参数辨识，与线路两端的电压幅值、电流幅值、电压相角和电流相角有关，因此根据上式，得到输电线路电阻相对于电压幅值、电流幅值、电压相角和电流相角的灵敏度公式，如下所示：

式中Um，Un，θum，θun分别表示两端电压幅值与相角，Im，In，θIm，θIn分别表示两端电流幅值与相角。利用Wolfram Mathematica软件对线路电阻参数的灵敏度进行计算，计算结果如表1和表2所示。

表1 线路电阻参数对线路首端（M侧）电气量变化的灵敏度计算结果

表2 线路电阻参数对线路末端（N侧）电气量变化的灵敏度计算结果

表1中，线路电阻参数对线路首端电压幅值变化的灵敏度比较大，即当电压幅值变化1%时，会造成电阻变化17.272%；而对电压相角、电力幅值和电力相角这三个参数变化的灵敏度相对比较低。

表2中，线路电阻参数对线路首端电压幅值变化的灵敏度比较大，即，当电压幅值变化1%时，会造成电阻变化23.174%；而对电压相角、电力幅值和电力相角这三个参数变化的灵敏度相对比较低。

4 电气量测量误差的仿真分析

本文利用Matlab软件，对某220kV输电线路获得双端的电气量数据进行仿真分析，研究电气量变化对线路电阻参数辨识结果的影响。由表1和表2可知，线路电阻对电压相角、电流幅值、电流相角这三类电气量变化的灵敏度较低，即这三类电气量的测量误差不会对线路电阻的辨识计算造成很大影响，因此本次仿真只对电压幅值变化所造成的影响进行仿真分析。

某220kV输电线路的首末端电气量原始数据曲线如图2～9所示。

图2 输电线路首端（M侧）电压幅值曲线

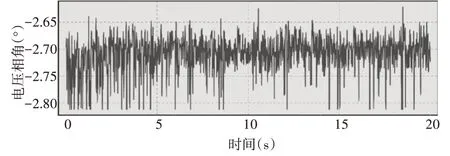
图3 输电线路首端（M侧）电压相角曲线

图5 输电线路末端（N侧）电压相角曲线

图7 输电线路首端（M侧）电流相角曲线

图9 输电线路末端（N侧）电流相角曲线

如图2和图4所示，线路首端和末端的电压幅值波动范围为0.3kV～0.4kV左右。如图6和图8所示，线路首端和末端的电流幅值波动范围为0.7A～0.8A左右，电流和电压的相角波动范围为0.15°。这种波动幅度表明该数据是线路正常运行时的数据，这些数据可以用于线路电阻参数识别计算。

图4 输电线路末端（N侧）电压幅值曲线

图6 输电线路首端（M侧）电流幅值曲线

图8 输电线路末端（N侧）电流幅值曲线

根据输电线路电阻参数等值模型，把上述实际电气量数据代入式（3）中，进行电阻参数识别计算，计算结果如图10所示。

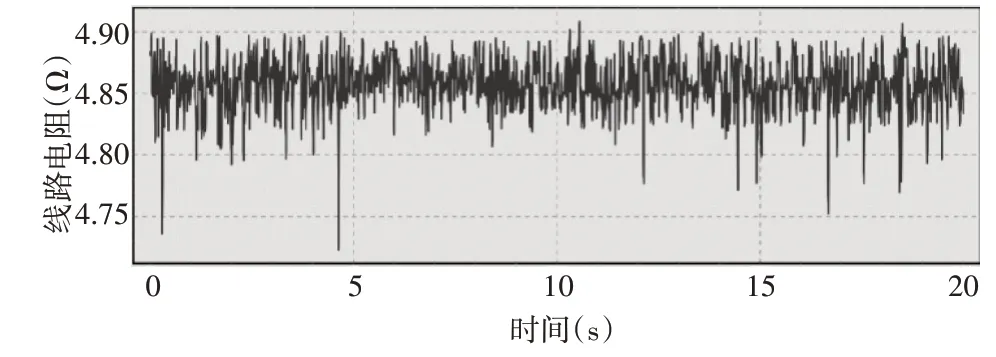
图10 输电线路电阻参数辨识计算结果

在实际测量中，测量用电压互感器的测量误差一般在0.2%以内，所以我们在原始电压幅值测量值（取平均值）的基础上，加入0.2%幅值平均值的均匀分布白噪声。加入0.2%噪声的电压幅值曲线如图11～12所示。

图11 输电线路首端（M侧）电压幅值加入噪声变化曲线

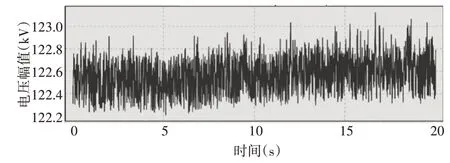
图12 输电线路末端（N侧）电压幅值加入噪声变化曲线

在电压幅值加入0.2%噪声，而电压相角、电流幅值和电流相角不变情况下，输电线路电阻辨识结果如图13所示。

图13 电压幅值加入噪声时的线路电阻辨识曲线

把电压幅值加入噪声时的线路电阻辨识结果与无噪声时的辨识结果进行相比，得到两次电阻辨识结果的相对误差变化曲线，对该曲线进行滑动平均处理，如图14所示。

图14 两次电阻辨识结果的误差曲线滑动平均效果

由图14比较可知，在考虑电压互感器测量误差最大的情况下，根据电气量对线路电阻参数进行辨识计算时，与电气量完全精确相比，辨识结果的相对误差仍保持在5%以内。因此输电线路两侧电压互感器、电流互感器的测量误差不会对线路电阻参数的辨识造成很大影响，该电阻辨识方法在整体趋势上具有较好的抗干扰性和较好的准确度。

5 结语

本文基于集中参数π型等值电路的输电线路参数辨识模型，建立了辨识参数受测量误差影响的灵敏度方程，根据该方程分析了电气量测量回路整体测量误差对输电线路交流电阻参数辨识准确性的影响。并且根据实测电气量数据，对电压幅值变化造成的输电线路交流电阻辨识不同结果进行了仿真分析。仿真结果表明，测量回路整体误差在0.2%以内时，不会对线路参数辨识的准确性造成很大影响，这种情况下的线路辨识结果可以为作为电网状态估计、潮流计算、网损分析和故障分析等电力系统计算的输入参数。本文所提的参数辨识可用性判断方法及仿真分析，为输电线路在线参数辨识的准确性和可用性提供了评判依据，有一定的参考意义。但线路参数辨识涉及到模型建立、参数选用、测量误差等多个方面，要想对辨识结果做全面的评估和判断，还需要进一步研究。