灰色马尔科夫预测模型在大学生转专业趋势中的应用*

游 琪

（广东科学技术职业学院 珠海 519090）

1 引言

大学生专业的选择与其职业生涯规划、兴趣爱好、人格特征、能力倾向、价值观、课程设置、学习难度等方面有关，大学专业的选择直接关系到学生未来的职业发展，这是一个非常重要的选择。一部分大学生与家长在选择专业时仅凭高考分数填报志愿，导致入学后发现专业选择与自身能力、兴趣、职业发展等差异较大，决定重新选择专业。

国家教育部颁发的《普通高等学校学生管理规定》中提出，对转专业的制定、实施主要由各高等学校执行，因而，该项工作逐渐成为学校学籍管理工作中的一项重点工作［1］。学校为了掌握大学生转专业发展态势，应相应地优化专业结构，强化专业教育，提升教学质量，激发学生学习兴趣，做好引导和教育工作等，保持各专业学生比例适应，为此需要对大学生转专业趋势进行预测分析。

2 问题分析

为了方便观察本文将从性别男女、是否跨学院、历年转专业和现专业人数排名前十数据、文理工学院划分四个方面来统计分析。通过对数据进行统计分析得出2016年、2017年、2018年、2019年转专业的学生总数。以每年的总人数为原始时间序列，建立灰色预测模型，预测未来几年内的转专业趋势变化。为了细化大学生转专业的趋势分析，按学生所属学院进行文理工三科划分，文科包含阿拉伯学院、国际学院、教育学院、经管学院、人文学院、外语学院、新闻学院、政法学院、中卫学院、美术学院、体育学院；理科包含数计学院、生科学院、资环学院、化工学院、物电学院、农学学院、数统学院；工科包含葡萄酒学院、土水学院、机械学院、信工学院。通过数据统计可计算出三大类之间的转换概率，得出转换概率矩阵，建立马尔科夫预测模型，预测各大类的学生转专业趋势。

3 建立灰色马尔科夫预测模型

3.1 数据的预处理

通过对数据进行初步处理后，得出的集成数据如表1所示。

表1 院系文理科划分表

2016～2019年男女生转专业情况如图1所示。从图1中，可以发现转专业人数逐年增加，呈现上升趋势。女生转专业人数比男生多，并且逐年增加速度要比男生快。

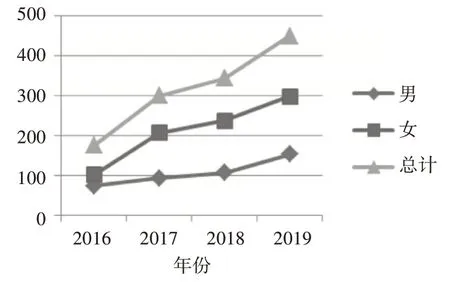
图1 2016-2019年男女生转专业情况

从转专业的学院进行分析，存在同学院内转专业和跨学院转专业两种情况，如图2所示。

图2 2016-2019年转专业学院变化情况

由图2可看出同学院转专业的人数几乎呈现直线上升趋势，同学院转专业人数慢慢增加，靠近不同学院转专业人数。同学院转专业人数历年上升在一定层面上反映了学生在选择专业时的思考增加，大方向决定好但是对于小方向的选择还是缺乏思考判断。

通过对2016～2019年学生的拟转入专业和现专业进行排序分析得出，拟转入专业和现专业排名前十的专业，如图3所示。

图3 2016-2019现专业人数排名前十

由图3可以看出，发现生物科学、旅游管理、交通运输、学前教育（教师教育）、市场营销这5个专业为热门转出专业，如图4所示。

图4 2016-2019年拟转入专业人数排名前十专业

从图4中得出滨海大学2016～2019年拟转入专业人数排名前十的专业，发现会计学、化学（教师教育）、经济学（金融）、汉语言文学（教师教育）、法学、生物学（教师教育）这六个专业为热门转入专业，其中教师教育类占大多数，可以推断大多数选择转专业学生更考虑毕业后的工作问题。

对学生转专业的文理工科进行分析，学生的现读学院的和拟转入专业所在学院的文理工科进行统计，得到表2。

通过表2可以计算出2016～2019年四年间，滨海大学转专业的人数中，文科转文科的人数占文科转专业人数的93.03%，理科转理科的人数占理科转专业人数的63.92%，工科转工科的人数占工科转专业人数的25.21%。将表2制作成折线统计图，如图5所示。

表2 现学院和拟转入学院文理工科情况

图5 现学院和拟转入学院文理工科情况

由图5可以看出，在转专业的人当中选择就读文科专业的人最多，选择就读工科的人数最少。大多数人都是选择在同类型的学院中换专业，仅有少部分人会选择换到不同类型的学院和专业。

3.2 模型的建立与求解

该理论通过灰色数据序列建立系统反应模型，并通过该模型预测系统可能的变化状态。其理论的实质是将无规律的原始数据进行累加生成，得到规律性较强的生成数列后再重新建模。由生成模型得到的数据再通过累加生成的逆运算累减生成得到还原模型，由还原模型作为预测模型［2～3］，该预测模型的优点是易于建立数学模型，需要的原始数据少［4～6］。但对于波动性较大的数列拟合精度较差，预测精度较低，在火灾中不能满足实际预测的需要，所以必须提高其预测精度。马尔科夫链根据系统不同状态之间的转移概率来预测系统的发展趋势，它和系统当前的状态相关，与系统过去的状态无关，适用于预测波动性较大的数列。因此，马尔科夫链可以较好地弥补灰色系统理论在实际预测中的缺陷［7～8］。

3.2.1 灰色预测模型

1）模型的建立［4，9～10］

设已知非负时间序列为X（0）=｛X（0）（1），X（0）（2），X（0）（3），…，X（0）（n）｝，做依次累加得X（1）（t）累加生成序列，即，t=1，2，3，…，n。

GM（1，1）模型的一阶常微分方程为

上式中，a为待辨识参数，也称发展系数；b为待辨识内生变量，也称灰作用量。

设原始序列X（0）及残差序列E的方差分别为S12和S22，则：

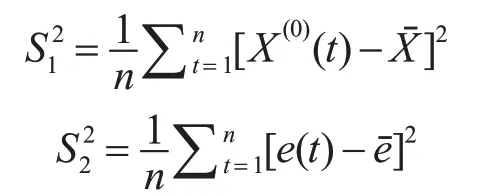
计算后验差比为C=S2/S1，通过对比下方参照表可以检验模型准确度，如表3所示。

表3 精度检验等级参照表

于是可得到灰色预测的离散时间响应函数为

还原为原始数列，预测模型为

将时间响应函数代入预测模型，将预测值还原即为

2）模型的求解

对各年学生转专业总人数做频数统计，得出2016年为174名、2017年为299名、2018年为342名、2019年为449名。

则原始时间序列X（0）=｛174，299，342，449｝，对数据进行累加求和，得出累加生成数列X（1）=｛174，473，815，1264｝。

建立灰微分方程：

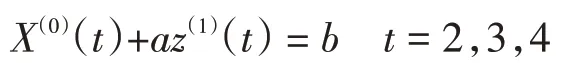
相应的GM（1，1）白化微分方程为

原始序列X（0）及残差序列E的方差分别为和，则：

利用Matlab对模型进行求解，得到S1=98.5114，S2=18.5919，a=-0.2118，b=221.6101，后验差比C=S2/S1=0.18873＜0.35，表明模型所得计算值与实际值之差并不离散，模型准确度高。

GM（1，1）模型的离散解：

还原为原始数列预测模型为

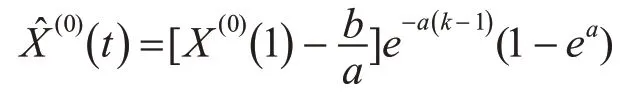
将上述求得a=-0.2118，b=221.6101代入模型解得：

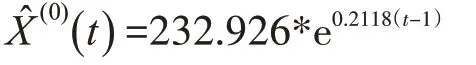
取t=5，即通过模型预测2020年转专业学生总数，得预测值=544；取t=6，即通过模型预测2021年转专业学生总数，得预测值=672。

综上所述，根据预测模型可以看出，每年的转专业总人数在一定的范围内与时间呈正相关的关系，转专业的趋势逐年上升。

3.2.2 马尔科夫模型

1）模型的建立［11～14］

对于需要计算的三科专业转入概率，不可能无限制的增长或降低，随着预测的年份增加，概率逐渐趋于稳定状态，符合马尔科夫链的性质要求，因此，可以考虑运用马尔科夫链建立学生转专业趋势的预测模型。

利用状态转移概率和系统的初始状态，建立如下马尔科夫预测模型。

设系统初始状态时，k=0。经过k次转移后，达到状态的概率为Si（k），则有∑Si（k）=1。

由切普曼柯尔莫戈诺夫方程得：

用向量表示：

可得递推公式：

设在n时系统为稳定状态，利用马尔科夫稳态分布模型可得到预测结果的极值Xn：

利用以上公式可对系统进行预测。

2）模型的求解

为了细化大学生转专业的趋势分析，按学生所属学院进行文理工三科划分。

根据滨海大学2015级转专业学生名单，获得相关资料，如表4所示。

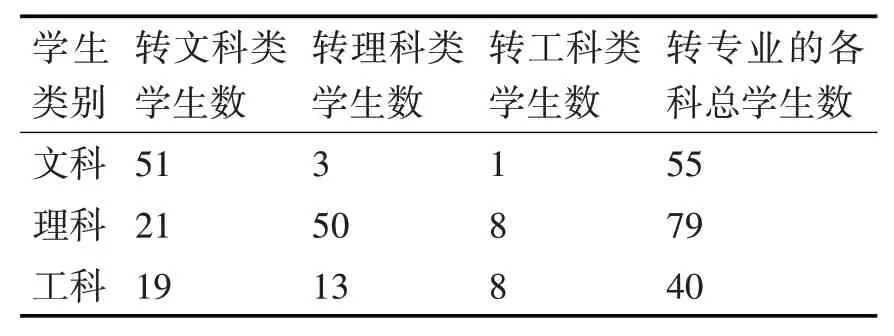
表4 2015级各科转入情况

从表4中可以看出，2015级文科类、理科类、工科类的转专业学生总数分别为55，79，40。由于各方面原因，部分学生开学后申请转专业，其中文科类转文科类的学生概率为51/55=0.927273，文科类转理科类的学生概率为3/55=0.054545，文科类转工科类的学生概率为1/55=0.018182。以同样的方法可计算出理科类，工科类学生转到其他类的概率。经过转专业后的三科实际学生数为91、66、17，实 际 转 专 业 概 率 为0.522988、0.379310、0.097701，即 初 期S（0）=（0.522988，0.379310，0.097701）。

利用转移概率，可得转移矩阵为

根据切普曼柯尔莫戈诺夫方程可预测2016级文科类、理科类、工科类学生转专业概率S（1）。

即2016级的文科、理科、工科专业转入概率的预测值分别为0.6322、0.3003、0.0675。

根据2016级实际的学生转专业数据，与预测值进行数据分析，得到如表5所示的结果。

表5 2016级转专业预测值与实际值的误差

可得三科预测值与实际值相对误差较小，可以认为用马尔科夫算法计算三科转入概率是可行的。

若有限状态马尔科夫链是不可约和非周期的，则它的平稳分布唯一，从任意的初始分布出发，当n＞∞时，Xn的分布必定趋向于此平稳分布。

4 结语

运用了灰色预测与马尔科夫预测，对Y大学转专业趋势进行了合理预测，分析出的结果在中、短时期精准度高，也足够直观。根据预测值进行分析得出，申请转入文科的学生人数占比始终最大，理科次之，工科最小，这个趋势可保持较长一段时间，故学校招生时可适当增加文科生的招收名额，理科与工科则适当减少名额。