基于坐标变换的圆柱体点云数据拟合方法*

袁 辉

（中铁第四勘察设计院集团有限公司 武汉 430063）

1 引言

三维激光雷达（Light Detection and Ranging，Li-DAR）测量技术是一种非接触、快速度、高精度和高密度测量数据获取技术［1～4］，已广泛地应用于智慧城市、工程测量等领域。从点云数据中提取各种所需的空间及属性信息是点云数据后处理的一项重要内容［5～7］，其中从点云数据中拟合圆柱体是工程测量中一个常见的问题［8～10］，例如管径的尺寸检测、立柱的直径测量和垂直度检测、隧道环片几何尺寸测量和形变检测等。

当前圆柱体的拟合方法主要有基于几何分析的拟合算法［10～12］、基于坐标转换的拟合算法［13～15］以及基于智能算法的拟合算法［16～17］等。基于几何分析的拟合算法直接从圆柱体方程的几何定义出发，建立误差方程进行最小二乘平差，但是由于误差方程的非线性的特点，拟合结果受参数初值影响较大，容易陷入局部收敛［18～19］。基于坐标变换的拟合方法是将圆柱体的轴线旋转到与竖直方向平行，然后投影到水平面上进行圆形拟合，文献［13～15］建立了基于坐标转换的非线性最小二乘平差模型，该方法也同样依赖于初值的选择。文献［16～17］利用遗传算法拟合圆柱体模型参数，但该算法参数多，容易早熟收敛，同时计算效率低。

本文针对点云数据的圆柱体的拟合问题，根据基于坐标转换的拟合算法思想，构造了旋转矩阵将三维的非线性的圆柱体拟合问题转换为二维的线性的圆形拟合，降低了处理的复杂度，同时利用迭代逼近法求解中轴线的方向向量，另外再根据拟合中误差进行点云噪声点剔除处理进行迭代拟合，提高了圆柱体模型参数拟合的准确度。

2 圆柱体拟合问题

在三维空间中，圆柱体是到其中心轴线距离为常数r的点集合，因此，圆柱体由以下7个参数唯一确定：圆柱体中轴线上的点po(xo,yo,zo)、中轴线方向向量s(a,b,c)、圆柱体半径r。约束方向向量s为单位向量，即a2+b2+c2=1，因此圆柱面的方程可以表示为

定义数据点集合P={p1,p2,…,pN}为三维激光扫描仪采集得到的圆柱体表面点云，其中N为点数，pj=(xj,yj,zj)，pj∈P，j∈[1,N]。在最小二乘算法拟合过程中，定义点的拟合误差为点到圆柱体中轴线的距离与圆柱体半径之差，表示为

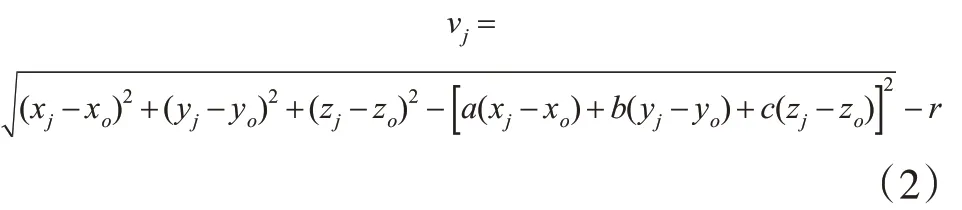
因此，采用最小二乘拟合使误差函数F值最小，即：

基于几何分析的拟合算法［11～12］对式的误差方程进行线性化处理，舍去高次项，然后按照高斯牛顿法迭代计算。由于式的误差方程包含根式，同时参数xo,yo,zo,a,b,c之间的相关性大，在参数初值不准确的情况下容易造成局部收敛，导致错误的拟合结果，因此非线性最小二乘拟合圆柱体过程中对参数初值的选择要求很高。

3 基于坐标变换的圆柱体拟合

根据基于坐标变换拟合圆柱体的思想［13］，将圆柱体的中轴线旋转到与z轴方向(0,0,1)平行，此时圆柱体在xoy平面上的投影为圆形，圆形半径与圆柱体半径相等。因此，一旦确定了中轴线方向向量s，便可将三维的圆柱拟合问题转换为二维的圆形拟合问题，而圆形拟合可以用线性方程直接平差处理完成，降低了计算的复杂度。

3.1 基于坐标变换的圆柱体拟合

定义圆柱体的中轴线方向向量s(a,b,c)绕x轴旋转角度θ∈[0,2π)，再绕y轴旋转角度φ∈[0,2π)后变换为z轴方向向量(0,0,1)，因此旋转变换矩阵R为

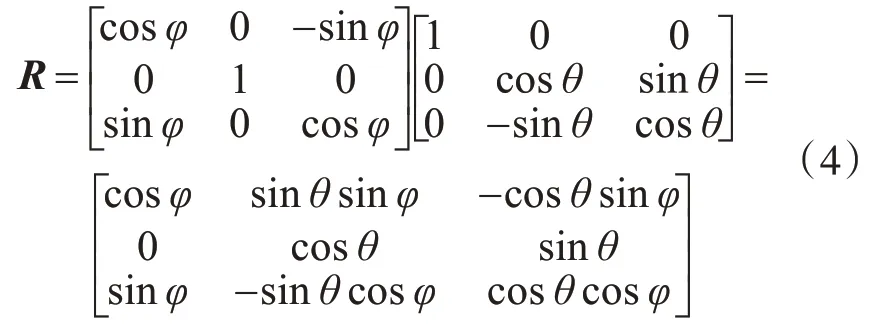
变换矩阵满足R-1=RT，另外方向向量s(a,b,c)需满足

求解得到中轴线方向向量s(a,b,c)为a=sinφ，b=-sinθcosφ，c=cosθcosφ。根据旋转矩阵R将点的坐标(x,y,z)变换为(x′,y′,z′)。

对于变换后的点坐标(x′,y′,z′)取x′和y′拟合二维平面圆形，圆形方程定义为

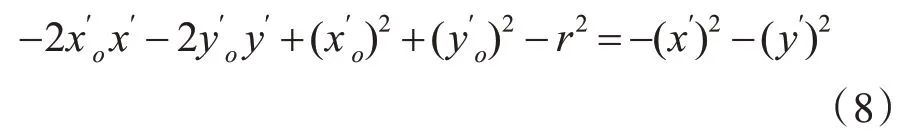
令A=-2x′o，B=-2y′o，C=(x′o)2+(y′o)2-r2，因此，式（8）可以转换为线性方程

对线性方程式（9）根据间接法最小二乘平差直接求解得到参数A、B、C的值，然后计算得到。其中拟合的圆形的半径r也是圆柱体的半径，然后将拟合的圆心坐标(x′o,y′o,0)进行反向坐标变换转换为圆柱体轴线上的点po(xo,yo,zo)。在拟合圆形过程中，定义点是pj=(xj,yj,zj)根据式（6）转换后的点，其拟合误差为

相应地，点云集合的误差函数F′为

3.2 迭代逼近法求解方向向量

根据上述基于坐标转换的圆柱体拟合算法，在已知中轴线方向向量s的情况下便能很方便地拟合得到圆柱体的7个参数，因此其中的关键问题是如何准确得到角度θ和φ，文献［13］通过建立整体的坐标转换误差方程进行非线性最小二乘进行迭代计算，计算过程复杂也需给定合适的参数初值，本文通过迭代逼近法求解θ和φ。

迭代逼近法解角度θ和φ的思路如下：初始给定角度值的值域范围和角度步长较大，先初步定位当前拟合误差最小的一组θ和φ角度值，然后在这组角度值邻域范围内采用更小的步长迭代查找新的最优角度值，直到两次拟合误差值差别足够小时则停止迭代。本文先根据角度θ和φ的不同取值，计算对应的拟合误差值F′，在F′最小时的那一组θ和φ值为最优取值，利用迭代逼近法求解θ和φ的具体步骤如下：

1）定义角度θ和φ在第k=1次迭代时的初始值域范围为2π，初始角度查找步长Δk=π/10，初始最优拟合误差，初始最优角度值为θbest=0和φbest=0，迭代精度ε=1×10-5。

2）根据当前角度步长Δk，在当前角度范围和内按步长遍历取值，即，，根据当前角度和进行坐标变换以及圆形拟合，计算当前拟合误差。

在上述迭代逼近法求解角度步骤中，在每一次的迭代过程中进行的拟合计算次数较少，同时每经过一次迭代，角度的值域范围就显著减小，同时当前最优的角度值的精度提高一个等级，可以很快地收敛到最优角度值。尽管利用迭代逼近法增加了拟合处理的次数，但在最小二乘拟合过程中，是对二维的平面圆进行线性方程的拟合处理，计算简单方便，也不会造成计算性能的显著下降。

3.3 圆柱体噪声点剔除

根据三维激光扫描测量得到的圆柱体点云数据，往往有较多的噪声点，如果不去噪直接拟合圆柱体的模型参数，会导致较大的误差。因此本文通过计算拟合结果的中误差值δ，剔除拟合误差超过3倍中误差的噪声点后再次进行拟合，然后重复该过程，直到无噪声点被剔除为止。在后续的迭代过程中，角度θ和φ的初始值域范围可以按上一拟合过程中的结果角度取一定的邻域范围，可以加快迭代逼近过程的收敛速度。

4 实验分析

为了验证本文提出的圆柱体拟合方法的有效性，同常规圆柱体拟合的最小二乘算法［12］进行对比实验，最小二乘算法按实际情况选取合适初值。实验数据为某一建筑圆形立柱的三维激光扫描点云数据，如图1所示，该立柱点云包含大约5000个点，点间距2cm。

图1 建筑立柱点云数据

在都不进行噪声点剔除情况下用不同算法进行圆柱体拟合，拟合结果如表1所示。

从表1中可以看出，两种算法中轴线上点(xo,yo,zo)差别较大是因为不同算法选取轴线点的方式不同，现将最小二乘算法的轴线点沿其轴线方向移动使zo=2.20020m，移动后最小二乘算法的xo=-2.2854m、yo=4.4846m，移动后两种算法轴线点距离差为0.1mm，差别很小。本文算法与最小二乘算法的拟合半径相差0.1mm，中轴线角度相差0.08°，拟合误差相差0.0002，二种算法结果很接近，是因为定义的误差目标方程实质是相同的，所以最终收敛拟合的结果基本一致。但是常规拟合算法需要在给定合适的初值情况才能正确收敛，而因此本文算法无需初值选择就能够准确地拟合圆柱体参数。

表1 立柱点云圆柱体拟合结果

图2为一地铁圆形盾构隧道环片的点云数据，点数74892个，点间距3cm，隧道设计半径2.75m，从图中可以看出点云中包含大量的非隧道轮廓的噪声点。

图2 隧道环片点云数据

采用本文的圆柱体拟合算法对该环片点云数据进行直接拟合和按本文方法进行迭代去噪拟合的结果如表2所示。

从表2中可以看出，未去噪直接拟合圆柱体的半径r=2.7005m，与设计半径2.75m相差很大，属于错误的拟合结果，拟合误差达到4285.4418。按照3倍的中误差δ=0.2392m剔除噪声点后，剩余70883个点，再次拟合得到圆柱体半径为r=2.7408m，拟合误差显著减小到311.3382。在重复迭代去噪拟合6次后，无新的噪声点被剔除，剩余67427个点，最终拟合半径r=2.7528m，与设计半径值接近，同时拟合误差值F′=10.1426，远小于未去噪时的拟合误差。因此通过计算拟合中误差然后按照3倍中误差限值进行去噪拟合能有效提高圆柱体的拟合精度，从而满足实际工程项目的需求。

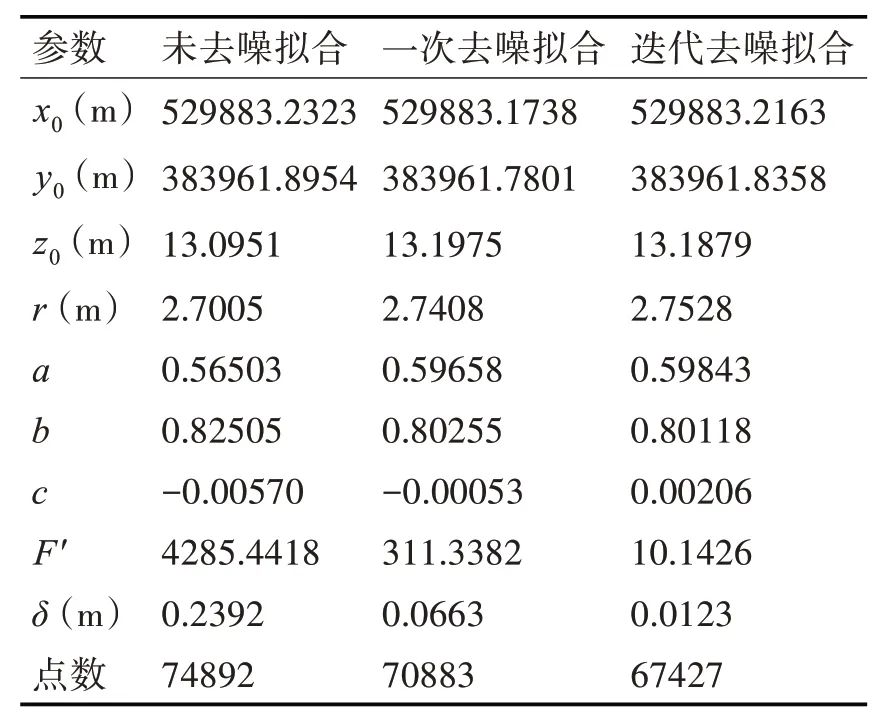
表2 隧道环片点云圆柱体拟合结果

5 结语

本文针对圆柱体点云数据的拟合问题，根据坐标转换拟合的思想，利用迭代逼近法准确求解圆柱体的中轴方向向量，然后根据中轴方向旋转点云数据到与竖直方向平行，将三维的非线性圆柱体拟合问题转化二维的线形圆形拟合问题，降低了拟合的复杂度。通过建筑立柱圆柱体点云数据的拟合实验，证明本文方法在无需给定初值情况下的拟合精度与正确拟合收敛的非线性最小二乘法的拟合精度相当。根据地铁隧道点云数据的实验，通过计算拟合中误差然后按照3倍的限差剔除噪声点后迭代处理能够有效提高拟合的精度，证明了本文圆柱体点云数据能够满足实际工程拟合精度的要求。