实时混合试验鲁棒时滞补偿方法的数值研究

宁西占，黄伟

（1.华侨大学 土木工程学院，福建 厦门 361021；2.福建省智慧基础设施与监测重点实验室（华侨大学），福建 厦门 361021）

混合试验源于1969 年日本学者[1]提出的拟动力试验方法，它将数值计算和物理试验通过在线的方式有机结合在一起，是评估结构在动荷载作用下性能的经济、实用的方法.通常，混合试验方法将待评估结构中具有较强非线性的部分取出在实验室进行物理加载，剩余部分在计算机中模拟.前者称为物理子结构，后者称为数值子结构，子结构间通过传递系统（通常是作动器）联系在一起.混合试验提出之初采用了慢速加载方式，并在逐步积分方法、误差传递等方面取得了一系列研究进展[2-4].

Nakashima 等在进行混合试验时对试件采用动力加载的方式，提出了实时混合试验，解决了速率相关型试件的混合试验问题[5].在实时混合试验中，数值计算、边界条件实现及数据采集等均需在十分短的时间步长内完成，以实现子结构间边界位移协调和力的平衡.受数据交互、模拟信号与数字信号间相互转换、作动器的动态性能以及作动器与试件间相互作用的影响，作动器接收的命令和实际响应之间往往不同步，这种现象通常称为时滞.时滞的存在将减弱实时混合试验的精度，甚至严重影响其稳定性[6].因此，一系列时滞补偿措施不断被用于抑制时滞的影响，如基于常时滞假设的预测方法[6]，基于经典控制理论的前馈、反馈及逆控制[7-9]，基于现代控制理论的滑动模态控制[10]、H∞控制[11]，以及基于反馈力修正的方法[12]等.近年来，自适应时滞补偿策略[13-16]也得到了广泛的关注.然而，基于控制理论的时滞补偿方法大多数具有模型依赖性，而反馈控制无法完全消除时滞的影响.此外，考虑到物理加载的动态特性、试件的非线性、噪声以及电压变化导致的供油压力变化等因素，前述时滞补偿方法效果被削弱.

针对以上问题，本文提出了一种鲁棒时滞补偿方法，并通过Benchmark 模型进行了初步验证[15].为深入分析鲁棒时滞补偿方法的性能，本文首先基于作动器的Benchmark 模型，采用线性物理子结构，对比研究了鲁棒时滞补偿方法和反馈修正的自适应时滞补偿方法；之后，讨论了鲁棒时滞补偿方法处理非线性物理子结构的能力；最后，基于考虑流量非线性的作动器模型，以磁流变阻尼器为非线性物理子结构，研究了考虑试验系统（作动器-试件系统）非线性时鲁棒时滞补偿方法的性能.

1 鲁棒时滞补偿方法

在已有的时滞补偿方法中，大多数具有模型依赖性，而数学模型不能考虑物理子结构的制造误差、观测噪声、外界扰动以及加载系统动态性能改变等因素.而在控制领域中，上述因素通常归为未建模动态和模型参数不确定性.因此，笔者提出了鲁棒时滞补偿方法，并将其应用于线性Benchmark 问题[15].该方法的原理如图1 所示，其中dD是期望位移，dm是测量位移，dc是命令位移，d 是外插预测位移.该方法中，时滞补偿器由H∞控制器和多项式外插两部分组成，前者用于改善被控对象的动态性能，得到一个稳定且具有鲁棒性的闭环系统，后者则用于进一步消除系统的时滞.

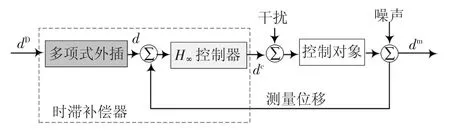
图1 鲁棒时滞补偿方法框图Fig.1 Block diagram of robust time-delay compensation method

1.1 基于混合灵敏度的H∞控制器

H∞控制是通过建立从广义输入到性能输出的性能指标传递矩阵F，并在Hardy 空间中以该性能指标的无穷范数为衡量标准进行优化，从而得到控制器的一种方法.标准H∞控制问题可通过对一般反馈控制问题进行性能加权获取，本研究中加权的反馈控制框图如图2 所示.这里，广义输入为位移d，性能输出为z=[z1；z2；z3]，性能指标为：

式中：S=1/（1+PK）为灵敏度函数；T=PK/（1+PK）为补灵敏度函数；P 是控制对象（包含作动器和物理子结构）；W1、W2和W3是性能加权函数，直接影响系统的追踪性能和鲁棒性.图2 所示控制问题的广义被控对象及状态空间实现为：

图2 加权的反馈控制框图Fig.2 Block diagram of weighted feedback control

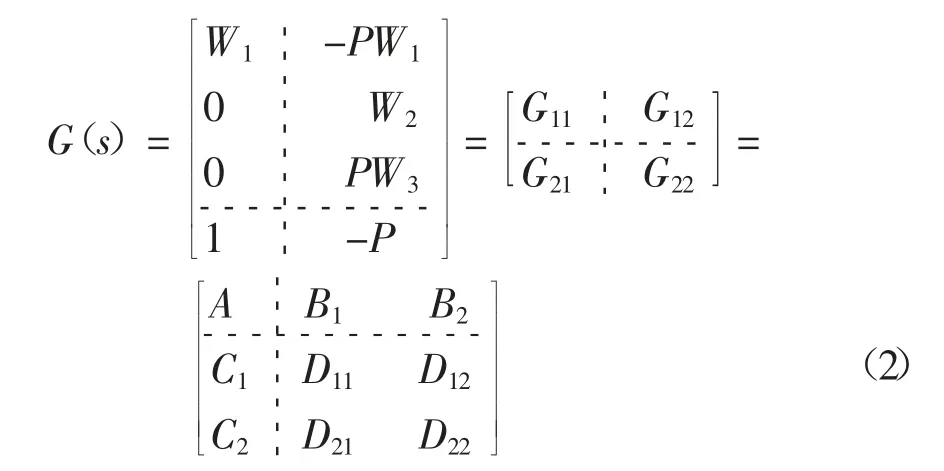
设计H∞控制器，即寻找一个控制器K，使得闭环系统是内稳定的，并且性能指标满足

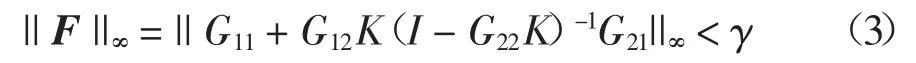
式中：γ 是一个给定的正数，下标“∞”表示无穷范数.设计H∞控制器有多种方法，如线性矩阵不等式法、DGKF 法等[17].本研究采用DGKF 法，即当系统（A，B2）为可镇定的，（C2，A）为可检测时，可通过求解两个黎卡提方程得到H∞控制器.

采用基于混合灵敏度的H∞控制设计时，控制器的追踪性能和鲁棒性直接受到三个权函数的影响.吴旭东和解学书[18]给出了权函数选取的一般性原则，这里不再赘述.需要强调的是，在进行控制器设计时，权函数W1应具有近似积分特性的形式，以实现在所关心的频率范围内系统具有较强的追踪性能和抗干扰能力；权函数W3在低频段远小于1 并且在高频段应具有近似s2特性，以实现对命令信号的追踪和对高频噪声的抑制.因此，本研究中权函数W1和W3具有如下形式：

式中：a1、a2、b1、b2和b3是常数，且a2是一个很小的正数，以使控制器具有积分特性.

1.2 多项式外插

H∞控制本质上仍是反馈控制，控制后系统必然仍有时滞存在.但采用H∞控制器对被控对象的动态性能进行修正后，系统将具有稳定的动态性能，具备较强的追踪性能和抗干扰能力，且系统在较宽频率范围内将具有稳定的时滞[11，15].通常，采用H∞控制修正后的新系统可看作常时滞系统，可采用经典的多项式外插法将该时滞进一步消除.

本研究中，多项式外插采用性能较好的三阶外插方法[19]，其表达式为：

式中：q1=1+11η/6+η2+η3/6；q2=3η+3η2/2+η3/2；q3=3η/2+2η2+η3/2；q4=η/3+η2/2+η3/6；η=τ/Δt，τ 是新系统的时滞，Δt 是积分步长.

2 作动器数值模型

2.1 线性模型

为推进实时混合试验的发展，由美国自然科学基金资助的混合试验多灾害工程研究体发布了实时混合试验的Benchmark 问题[20]，用于评估不同时滞补偿方法的性能，尤其是鲁棒性.该Benchmark 问题建立在实际试验系统之上，待模拟结构是一个三层两跨的钢框架结构，刚度矩阵为KS=[2.605 5，-2.313 4，0.593 7；-2.313 4，3.256 1，-1.442 0；0.593 7，-1.442 0，0.926 7]×107N/m，采用集中质量矩阵，每层质量相同，并以底层左跨为物理子结构；同时，Benchmark 提供了电液伺服作动器的线性模型，将液压伺服阀、液压作动筒和力/位移传感器等元件以集中参数表示，物理子结构是线性试件，如图3 所示.图中α1、β0、β1和β2与液压伺服阀相关，α2与自然速率反馈相关，α3与液压作动筒相关，mp、cp和kp是物理子结构的质量、阻尼和刚度系数.为考虑液压传递系统、传感器与控制实现硬件和试验子系统等的不确定性，参数β1、β2、α3和kp采用服从标准正态分布的随机变量来描述.上述参数取值及其分布情况见表1.

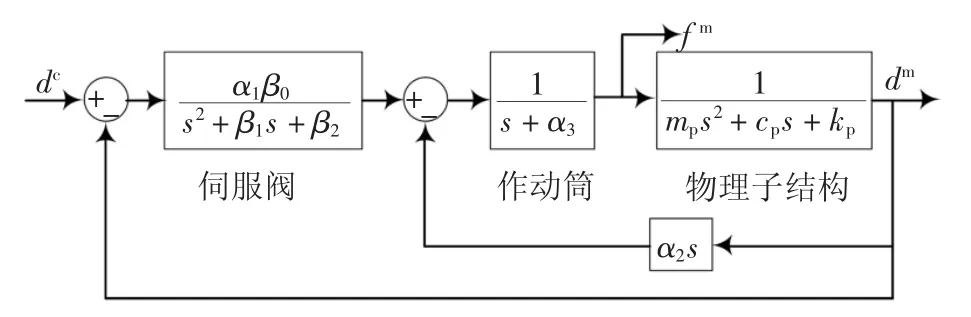
图3 Benchmark 问题中线性作动器模型[20]Fig.3 Linear model of the actuator in the Benchmark problem[20]

表1 作动器线性模型参数值[20]Tab.1 Parameter value of the linear actuator model[20]

2.2 考虑流量非线性的模型

作动器线性模型无法考虑加载系统使用过程中非线性引起的时滞变化，而流量引起的非线性在电液伺服系统中占主要成分.Zhao 等[21]提出的作动器模型可以有效考虑上述非线性，如图4 所示.图中，xv是伺服阀位移，Q 是流量，p 是负载油压，Ka是油的压缩系数，Cl是油的泄露系数，A 是活塞面积.伺服阀的传递函数为：

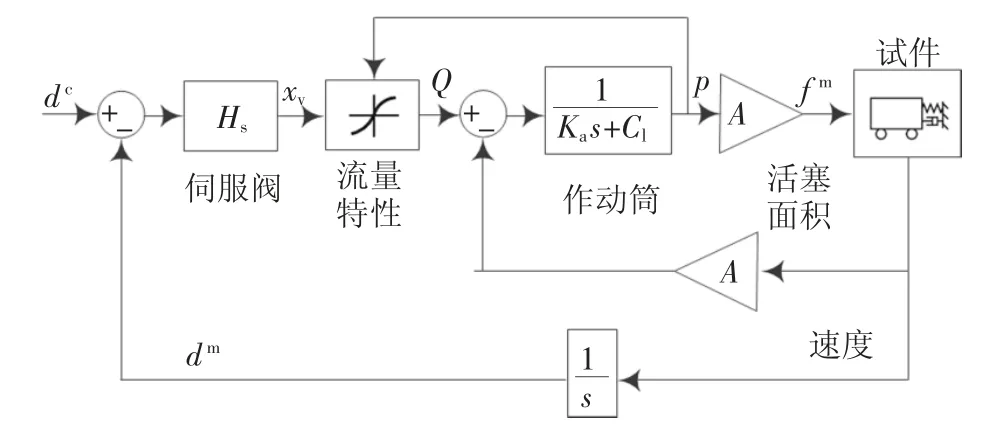
图4 非线性作动器模型[21]Fig.4 Nonlinear model of the actuator[21]

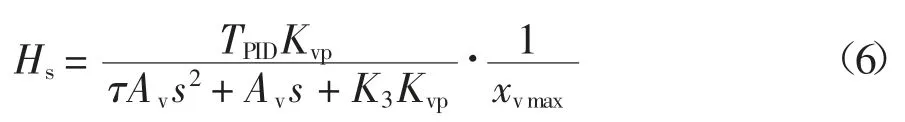
式中：TPID是模拟控制器传递函数，通常只取比例增益；Kvp是阀的增益系数；xvmax是最大阀芯位移；Av是滑阀阀芯面积；K3是内置位移传感器灵敏度系数；τ是滑阀时间常量.流量非线性关系及作动器相关参数分别见表2 和表3.

表2 阀芯开口与流量非线性关系[21]Tab.2 Nonlinear relationship between spool opening and flow[21]

表3 作动器非线性模型参数值[21]Tab.3 Parameter value of the nonlinear actuator model[21]

3 模拟结果与分析

3.1 作动器线性模型工况

为考察子结构划分对实时混合试验稳定性和精度的影响，Benchmark 问题给出了4 种子结构划分方式，楼层质量分别为1 000 kg、1 100 kg、1 300 kg 和1 000 kg，相应于每一种楼层质量，对应的阻尼比分别为5%、4%、3%和3%.对每一种子结构划分，考虑了El Centro 波、Kobe 波和Morgan Hill 波等3 种地震动记录，地震波的调幅均为0.4g，并分别完成了21次虚拟实时混合试验，共计252 次虚拟实时混合试验，以验证鲁棒时滞补偿方法的有效性和鲁棒性.同时，本文还研究了物理子结构进入非线性，并考虑恢复力模型为Bouc-Wen 模型时补偿器的性能.需要说明的是，本文采用了Kalman 滤波器对含噪声的位移信号进行滤波.

3.1.1 补偿器设计

以图3 所示系统为控制对象，完成了鲁棒时滞补偿器的设计.经试算，设计H∞控制器的3 个权函数为：

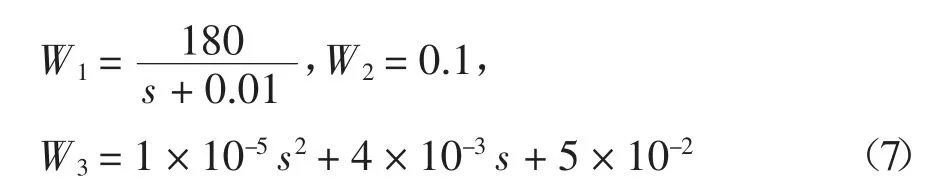
最终，经过29 次迭代得到可行解，其中最优γ值为1.522，相应的控制器为：

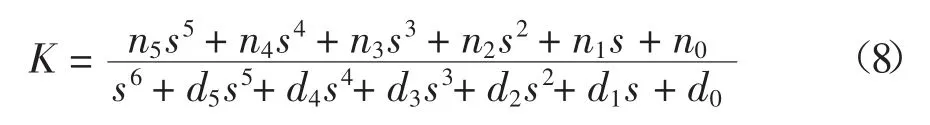
式中：n5=3.94 × 106，n4=1.703 × 109，n3=1.139 ×1012，n2=3.151 × 1014，n1=7.355 × 1016，n0=2.933 ×1018，d5=2.615 × 105，d4=2.935 × 108，d3=2.136 ×1011，d2=9.397 × 1013，d1=2.427 × 1016，d0=2.369 ×1014.

经H∞控制器修正后系统的动态性能如图5 所示，为方便比较，无控系统的性能也在图中给出.从图5 中可以看出，在关心的频率范围内，被控后系统具有稳定的幅值，且该幅值接近于0 dB，极大地改善了系统的追踪性能；从时滞图中可以看出，无控系统的时滞较大且变化明显，而被控后系统在较宽的频率范围内具有稳定且较小的时滞.以上分析表明，被控后系统具有稳定的动态性能，且可被看作常时滞系统.被控后系统时滞大小为0.008 4 s，因此，在多项式外插中η=34.406 4.

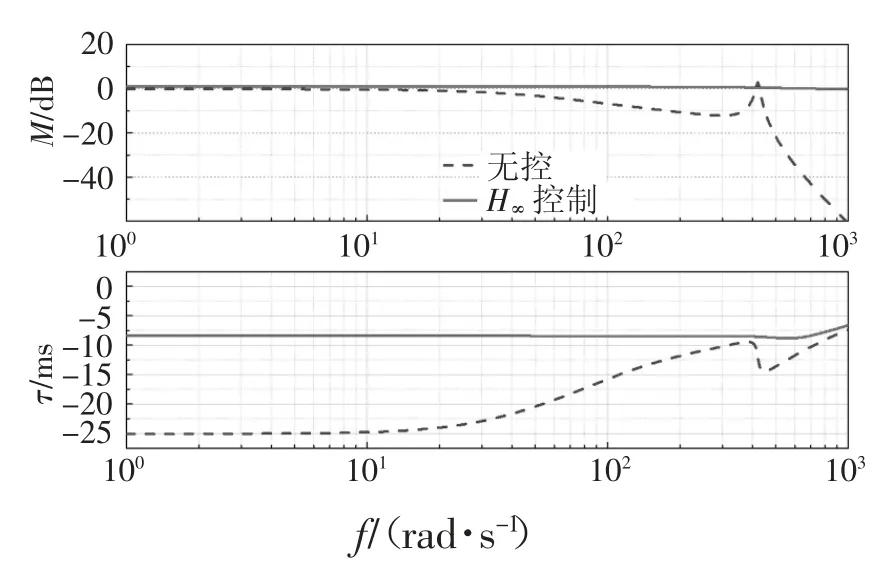
图5 系统动态性能Fig.5 Dynamics of the loading system

3.1.2 线性物理子结构

图6 给出了在El Centro 地震激励下楼层质量和阻尼比分别为1 000 kg 和3%的实时混合试验中作动器的追踪性能，其中参考位移是由数值子结构计算得到的位移.从图6（a）中可以看出，实测位移与参考位移吻合良好；从图6（b）可以看出，实测位移与参考位移几乎完全重合，表明本文所提时滞补偿方法具有良好的追踪性能.

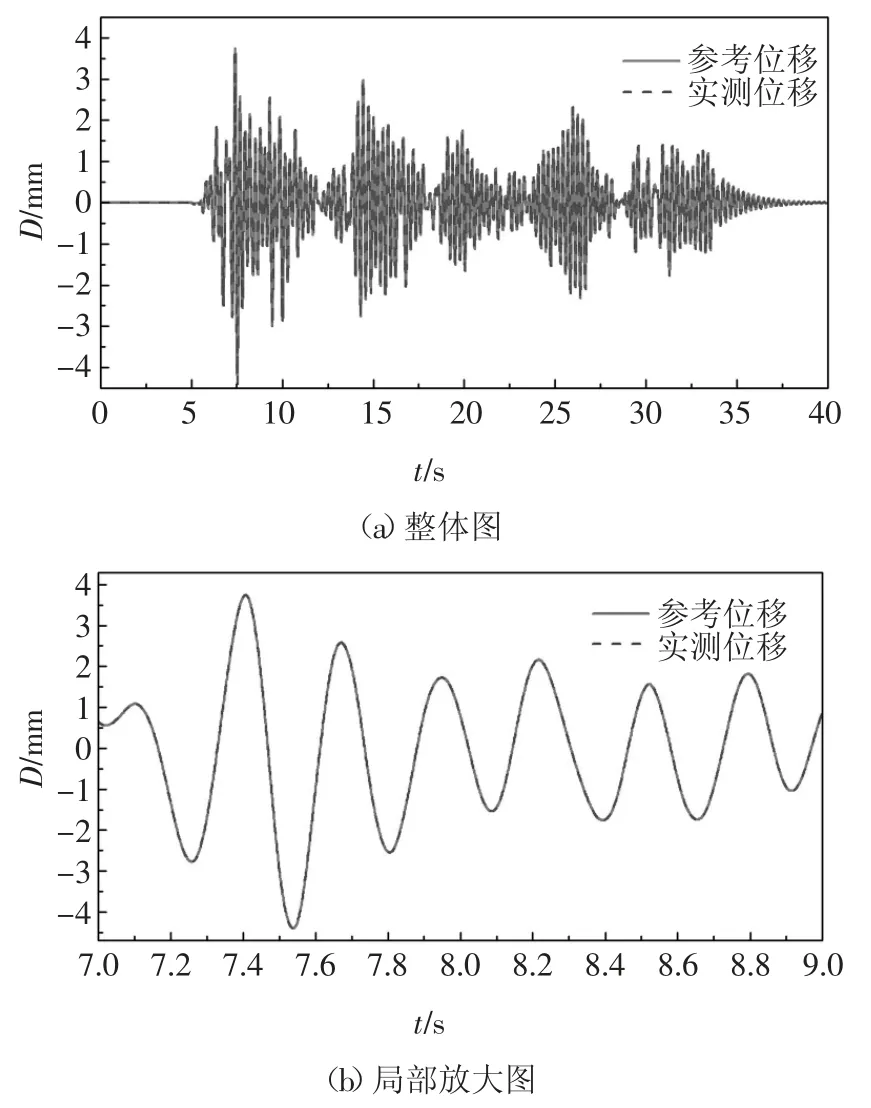
图6 线性作动器的追踪性能Fig.6 Tracking performance of the linear actuator

本文采用鲁棒时滞补偿方法的虚拟实时混合试验结果与文献[22]的结果进行了对比，如图7 所示.图中结果来自在El Centro 地震激励下虚拟实时混合试验的统计值.其中，误差指标J2和J3反映了作动器的追踪性能，分别是均方根误差和峰值追踪误差；误差指标J4、J5和J6分别是第一、第二和第三层位移的均方根误差；J7、J8和J9分别是第一、第二和第三层的峰值误差.J2～J9的定义参见文献[20].从图7（a）中可以看出，在8 个误差指标的统计均值中，本文方法的最大值均小于5%，而文献[22] 的方法则均大于5%，且J4的最大值高达30%，表明本文方法具有较好的追踪性能，可以大幅提高模拟精度.从图7（b）可以看出，除误差指标J6略大于文献[22]的方法外，本文方法的方差整体上是最小的，表明本文方法具有较强的鲁棒性.

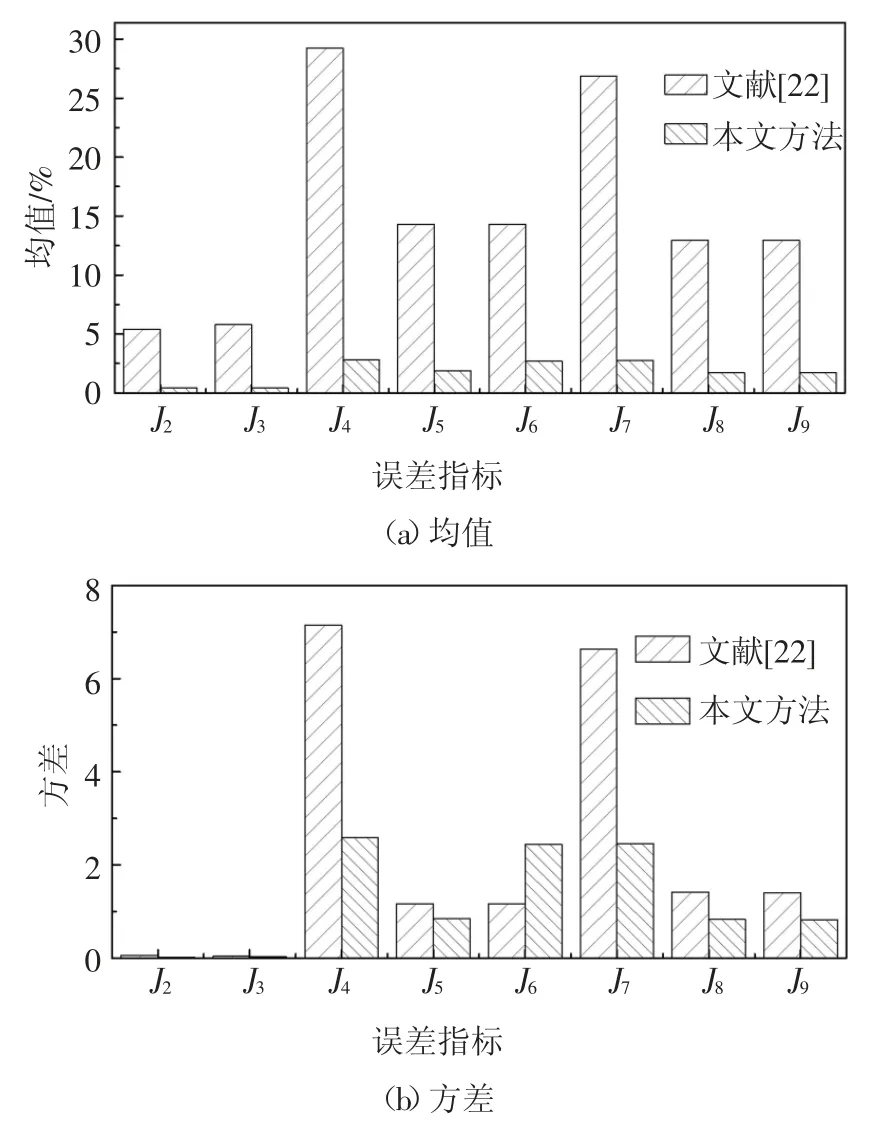
图7 不同方法误差指标直方图Fig.7 Histogram of error criterion under different methods

3.1.3 非线性物理子结构

在虚拟实时混合试验中，记录了非线性物理子结构的实测位移和实测反力，得到其滞回曲线，如图8 所示.从图中可看出，物理子结构进入了较强的非线性.同时，本文对252 次虚拟实时混合试验所得的均方根误差和峰值追踪误差进行了统计分析，得到了误差的累积分布函数，如图9 所示.从图中可看出，均方根误差的范围为0.6%～1.3%，而峰值追踪误差则为0.7%～1.5%；且当概率小于0.8 时，均方根误差和峰值追踪误差的值分别小于1%和1.25%.值得说明的是，采用鲁棒时滞补偿方法后，系统的计算时滞为0 ms.由于试件非线性的影响可归为模型的参数不确定性和未建模动态特性，而H∞控制可以很好地处理这些不确定性，因此本文方法对非线性试件依然具有较强的追踪能力.

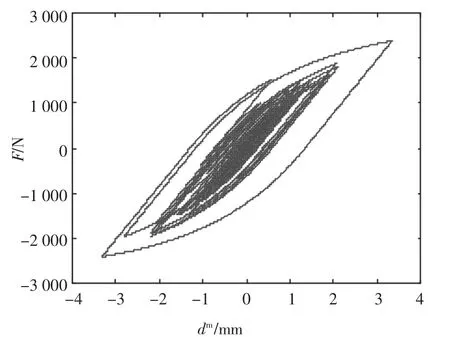
图8 滞回曲线Fig.8 Hysteretic curve

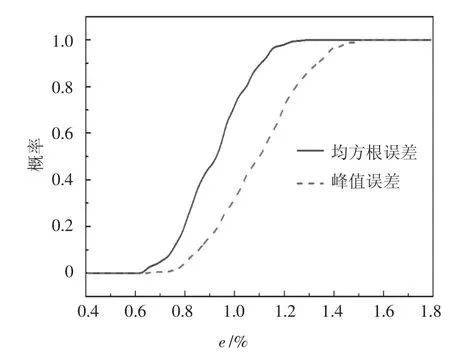
图9 误差的累积分布函数Fig.9 CDFs of the errors

本节采用结构第三层位移响应来讨论实时混合试验的模拟精度.由样本统计和核密度估计[23]得到的均方根误差和峰值误差的统计直方图与概率密度函数曲线如图10 所示，其中，在对概率密度进行估计时，核密度估计方法的核函数为正态分布函数，窗宽由样本的数目确定.从图中可以看出，采用核密度估计得到的两种误差指标的概率密度函数与由样本统计得到的直方图具有较好的一致性，且均方根误差和峰值误差的分布范围较小，分别集中在0%～7%和0%～5%.同时，从图中可以看出，均方根误差大于10%和峰值误差大于6%的概率远小于0.05.结果表明，采用鲁棒时滞补偿方法的实时混合试验，模拟结果的精度得到了很大改善，且表现出较强的鲁棒性.

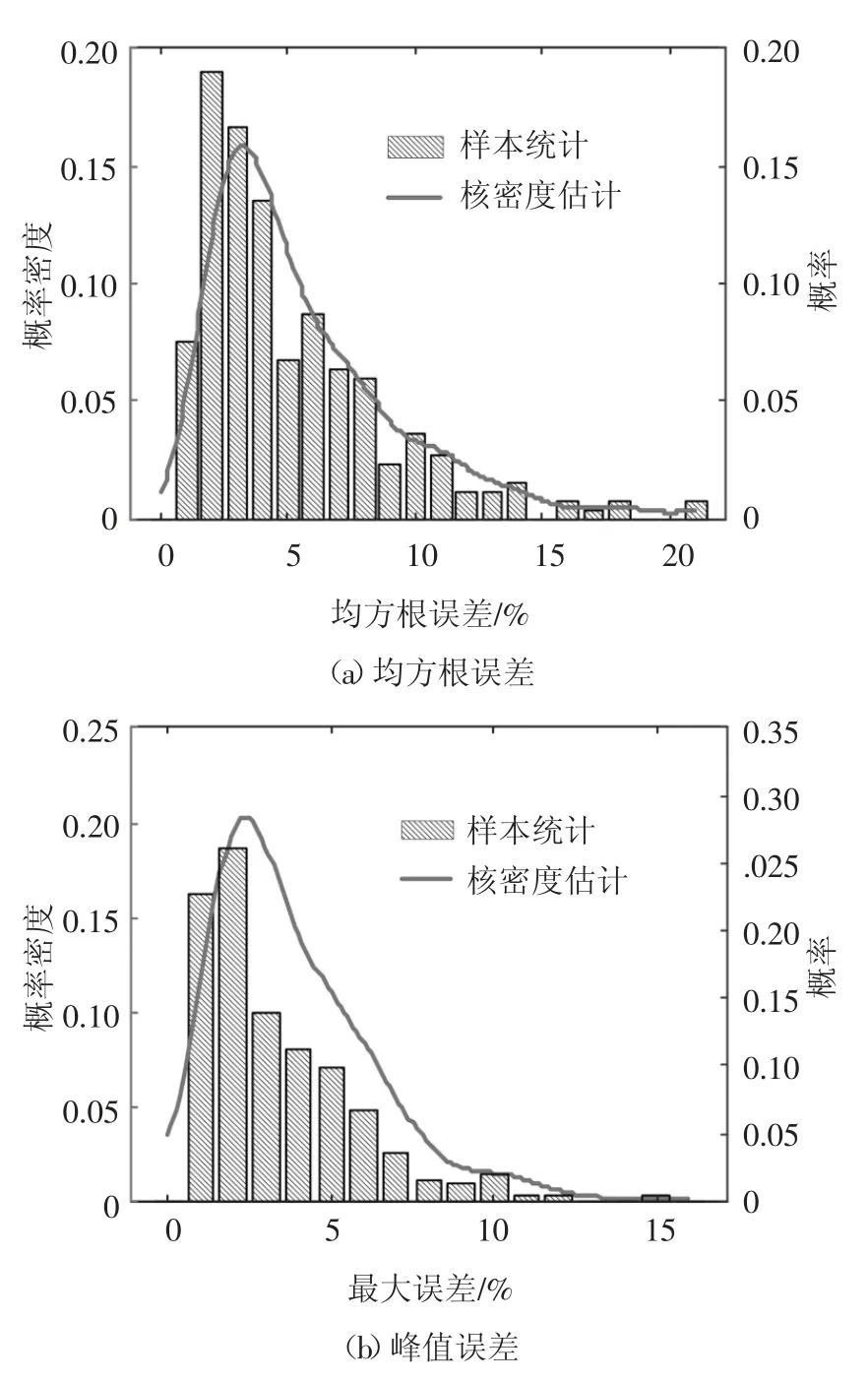
图10 位移误差的概率分布Fig.10 Probability distributions of the displacement errors

3.2 作动器非线性模型工况

在本工况中，参考结构是一个三层单跨的钢框架结构，并在底层安装有一磁流变阻尼器.参考结构每层的质量为20 250 kg，刚度矩阵为KS=[9.933 3，-5.662，0；-5.662，1.134，-5.662；0，-5.662，5.662]×106N/m，阻尼矩阵C=[724 2，-206 9，0；-206 9，4 139，-206 9；0，-2 069，2 069]Ns/m.物理子结构为磁流变阻尼器，采用Bouc-Wen 模型描述，即：

式中：αb=2 888.78 N；cb=6 400 N/A2；γz=200/m；βz=200/m；n=2，p=5 000/m.

3.2.1 补偿器设计

在进行虚拟混合之前，对试验系统输入幅值为0.01 m、频率为0～40 Hz 的正弦扫频信号，识别得到试验系统的线性数值模型为：

之后，以式（11）为控制对象，进行补偿器设计.经试算，设计H∞控制器的3 个权函数为：

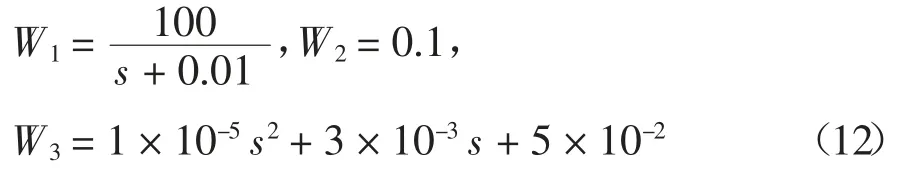
经过26 次迭代得到可行解，其中最优γ 值为0.783，相应的控制器为：

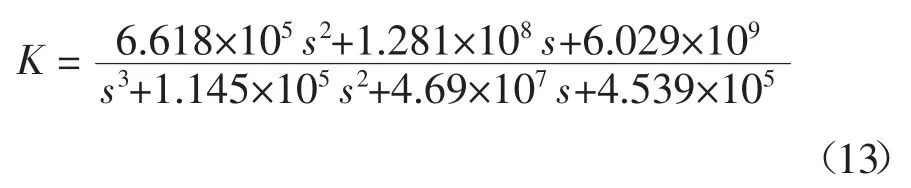
此时，新系统的时滞大小为0.007 8 s.因此，在多项式外插中，η=7.8.

3.2.2 模拟结果分析

在El Centro 地震激励下，作动器的追踪性能如图11 所示.从图11（a）中可以看出，作动器的测量位移与期望位移吻合良好；从11（b）的局部放大图可以看出，二者完全重合，表明作动器具有较强的追踪性能；从图11（c）给出了期望位移与测量位移的关系图，其中直线斜率为45°，进一步表明，鲁棒时滞补偿方法在处理作动器非线性和物理子结构非线性时依然具有较强的追踪性能.

图11 非线性作动器追踪性能Fig.11 Tracking performance of the nonlinear actuator

4 结论

为改善实时混合试验的稳定性，提高模拟精度，提出了鲁棒时滞补偿方法，并将其应用于解决线性问题的时滞补偿.基于前期工作，本文针对非线性问题开展了深入细致的研究，主要结论如下：

1）经H∞控制后试验系统的时滞明显减小，动态性能得到了极大改善；在关心的频率范围内，新系统可近似看作常时滞系统，且该时滞可采用多项式外插进一步消除.

2）考虑液压传递系统、传感器与控制硬件以及物理子结构等的不确定性和非线性时，经本文方法修正后的试验系统依然可几乎完全实现期望位移，使实时混合试验的模拟精度大幅提高，且表现出较强的鲁棒性.

3）虽然鲁棒时滞补偿方法具有较强的追踪性能和鲁棒性，但本文只完成了数值研究，该方法在真实试验中的性能有待进一步验证.