考虑防火门易损性的震后火灾模拟

王海东，袁佳欣

（1.建筑安全与节能教育部重点实验室（湖南大学），湖南 长沙 410082；2.湖南大学 土木工程学院，湖南 长沙 410082）

地震过后往往易发生次生灾害，难以控制且损失巨大.例如：1923 年日本关东大地震、1999 年台湾集集大地震、2008 年汶川地震、2011 年日本地震和2014 年智利地震等，震后引发大火，火灾造成建筑物损坏甚至倒塌，因而震后火灾结构的性能已成为国内外学者研究的一个热点.Jelinek 等[1]对钢框架在震后火灾下的反应与仅受火灾影响时结构的反应进行对比研究；Memari 等[2]提出一种基于概率性能的地震火灾分析框架，并利用该框架分析钢结构在地震和火灾连锁危害下的反应，同时研究火灾荷载密度等因素对结构失效概率的影响；Suwondo 等[3]研究了不同的火灾位置和地震破坏对荷载重分布路径和结构倒塌的影响；张文[4]通过模糊数学方法建立震后建筑火灾危险性评估模型，研究震后火灾对建筑结构的影响；毛小勇等[5]对轻钢-混凝土组合梁在标准升温下进行了抗火性能的研究；李强等[6]对先后经历地震和火灾作用的破坏形态、损伤机理进行分析，研究损伤指数对圆钢管混凝土柱震后耐火极限的影响.然而，从已有的研究中发现，研究者对于火灾发生的位置、温度分布，尤其是与火灾温度密切相关的燃烧物数量、分布、防火分区等等都是根据自己的假定而并不与建筑本身的信息相关，缺乏一定的合理性.与此同时，基于性能的抗震设计开始得到广泛的重视和发展[7]，笔者发现部分学者将建筑信息模型（Building Information Modelling，BIM）技术引入到火灾分析中，具有参考意义.

王婷等[8]将BIM 模型导入火灾模拟软件PyroSim中，实现简化火灾建模；陆扬[9]将BIM 技术运用到性能化防火设计中，实现了消防性能相关模拟；杜二峰等[10]设计建造缩尺比为1 ∶4 的门式刚架厂房模型，测量其模型内部各关键位置的热空气和钢构件温度.但仅考虑消防性能并未将非结构构件考虑于结构有限元模型中，故由此评估建筑整体防火性能可能缺乏安全性.且随着人们对建筑使用性的要求不断提高，利用基于FEMA P-58 的抗震性能评估方法，开始专注于非结构构件的评估是抗震性能评估的趋势.而防火门这一非结构构件是建筑在发生火灾时防止火灾蔓延的重要措施，地震发生将导致门有不同程度的破坏，从而影响结构温度场分布，最终影响结构的整体性能，因此通过有限元模型与该非结构构件进行联结，并对建筑整体的防火性能评估应值得关注.Xu 等[11]利用BIM 和美国抗震设计标准FEMA P-58 开展了建筑消防喷淋系统的震害评价，表明其建筑抗火性能与未考虑地震作用时有明显区别.但是，假定火灾位置进行火灾模拟，未将建筑内燃烧物与火灾位置进行关联，且未明确防火分区，难以得出震后火灾温度场的真实分布，可能缺乏合理性.

本文探讨一种利用BIM 技术和FEMA P-58 的考虑非结构构件破坏的次生火灾模拟方法，定量评估由于门损伤对火温分布的影响.该方法基于BIM快速准确地建立建筑火源信息模型，并通过FEMA P-58 的抗震性能评估方法评估震后门损伤的情况，进而通过Pyrosim 模拟分析防火门破损程度对火灾温度分布的影响，得到基于燃烧物与火灾位置关联下的真实温度场分布，为后续震后火灾结构整体性能研究提供基础.

1 建模分析

1.1 建模思路

考虑震后防火门破损的火灾温度模拟主要包括2 种不同的模型：①研究地震作用下非结构构件性能的有限元模型；②反映建筑物实际防火分区和燃烧物信息的火灾模拟模型.

如何将2 种独立分割的模型信息统一，本文提出了基于BIM 技术建立综合的建筑信息模型的方法，将以上2 种模型有效联结，具体思路见图1.该思路核心为建筑BIM 信息模型，即为实现火源信息化的关键，并利用FEMA P-58 得出非结构构件的易损性分析，同时结合有限元模型中结构时程分析得出门损伤概率模型，并利用火灾模拟软件FDS 模拟震后火灾，分析得出该模型温度的影响，更有利于将地震及震后火灾结合考虑.其中，有限元模型主要解决地震作用下非结构构件的破损分析问题；FDS 火灾模型主要解决火灾模拟分析以及温度实时分析问题；BIM 建筑信息模型主要提供结构信息、建筑防火分区、防火门破损位置、状态以及建筑火源分布情况，并贯穿于整个分析流程，为该建模思路的核心模型.

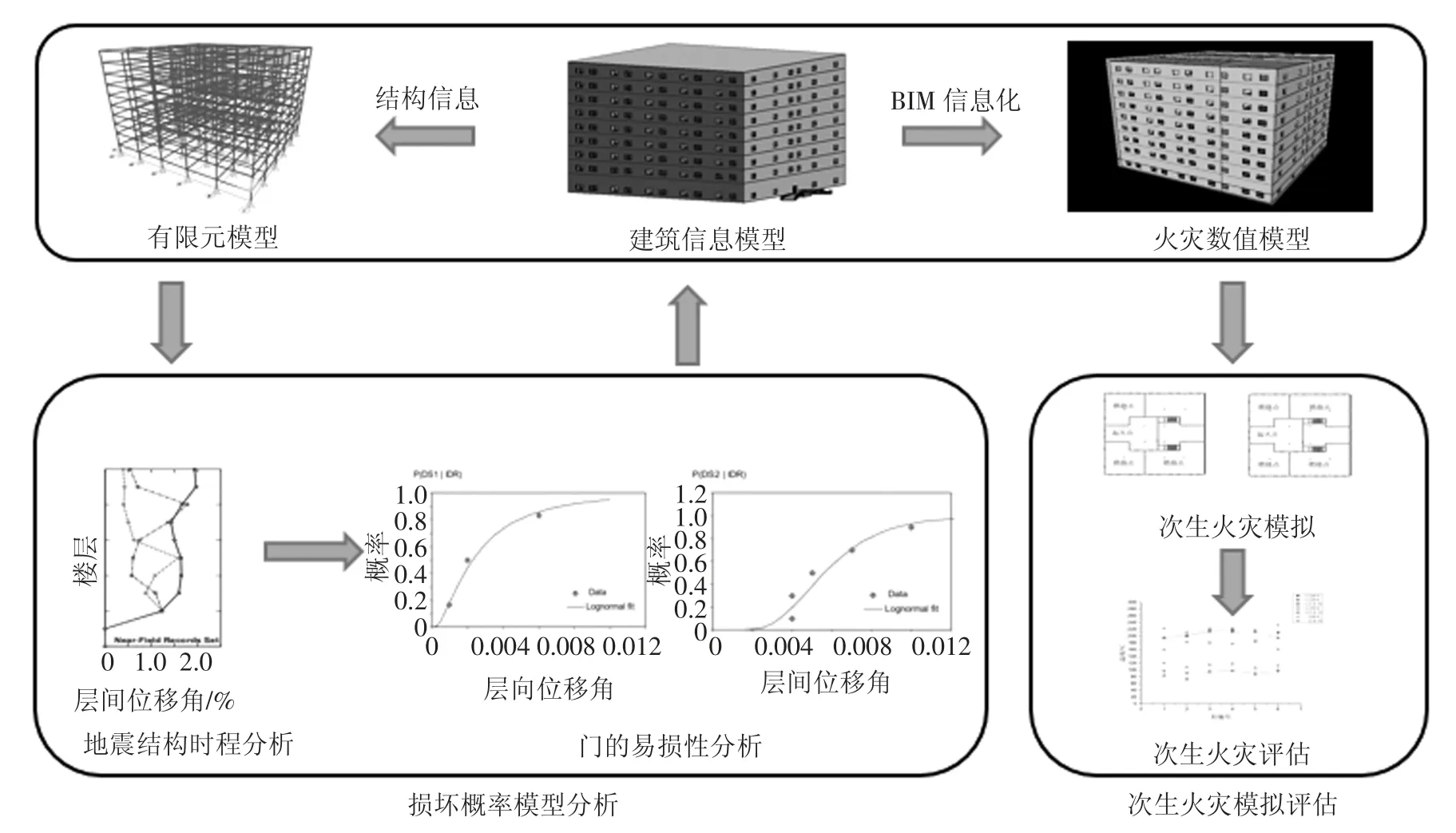
图1 模型评估方法Fig.1 Model evaluation method

对于体量较大、非结构构件较多且需要建立建筑火源信息的模型，直接建立含有建筑火源信息的火灾数值模型的工作量庞大，故将建筑内火源信息建立于BIM 模型中，从而为整体火灾模型的火源信息提供精细化的数据基础，进而通过格式的转换将其导入火灾模拟软件中得到建筑火源信息FDS 模型.将BIM 模型转换为FDS 模型，就是利用BIM 软件将模型导出为fbx 文件，再导入至图形化操作软件PyroSim 中，软件将正确识别文件格式，并按构件完成分组，此时对模型设置网格数量并对各构件材料属性进行定义，最终运行.

该模型充分实现BIM 技术“一模多用”的特点，减少了直接利用PyroSim 建立FDS 模型的复杂流程，而许镇等[12]，采取直接建模及转换生成FDS 模型的方式分别进行火灾模拟，模拟得出同一位置的烟气浓度曲线图，两种方式得出的结果基本一致，证明该转换方式具备较高的准确性.

1.2 模型建立

1.2.1 BIM 模型建立

本文将以9 层Benchmark 模型为例，利用Autodesk Revit2017 进行建筑建模，图2 为该建筑的三维BIM 模型，模型体现建筑功能分区、建筑火源信息、结构全部信息，且各层采用相同的平面布局.图3为该建筑的平面布置图.根据美国防火规范NFPA 5000-2012 将在该建筑每层设置6 个防火分区，图4为各层平面防火分区分布图.

图2 三维BIM 模型Fig.2 3D BIM model

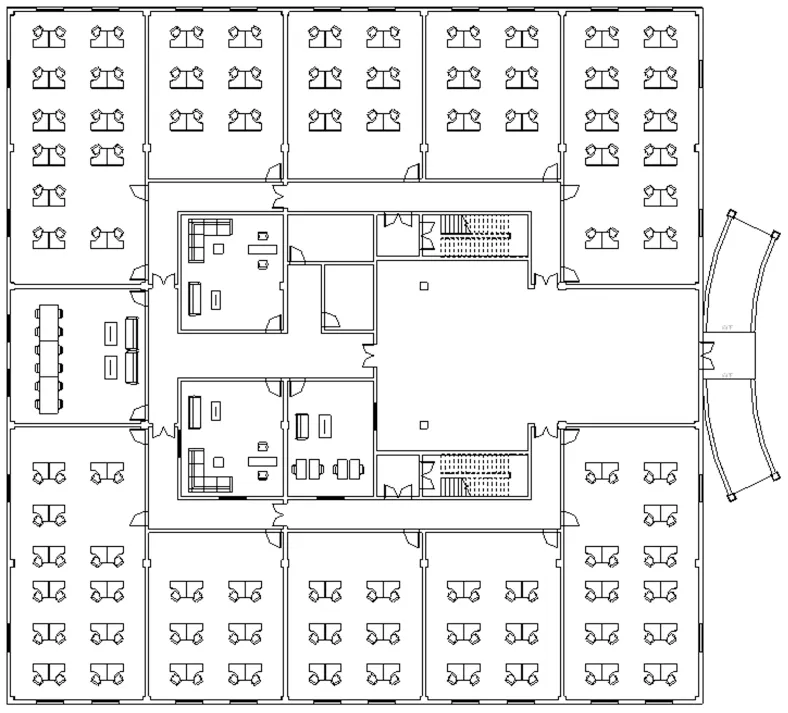
图3 建筑平面布置图Fig.3 Building layout plan

图4 防火分区分布图Fig.4 Fire compartment plan

1.2.2 有限元模型创建

本文选用9 层Benchmark 模型，平面尺寸为45.73 m×45.73 m，X 方向、Y 方向对称，各5 跨，每跨9.15 m，首层高度为5.49 m，标准层高度为3.96 m，梁、柱单元材料分别采用的是屈服强度为248 MPa 和345 MPa 的工字钢，表1 给出了9 层Benchmark 钢框架结构模型的构件尺寸，详细参数见文献 [13].利用SAP2000 有限元软件对9 层Benchmark 三维框架模型进行结构分析，阻尼比ζ=0.05.抗震设防烈度为8 度（0.20g），场地类别为Ⅱ类（D类），场地分组为第1 组.

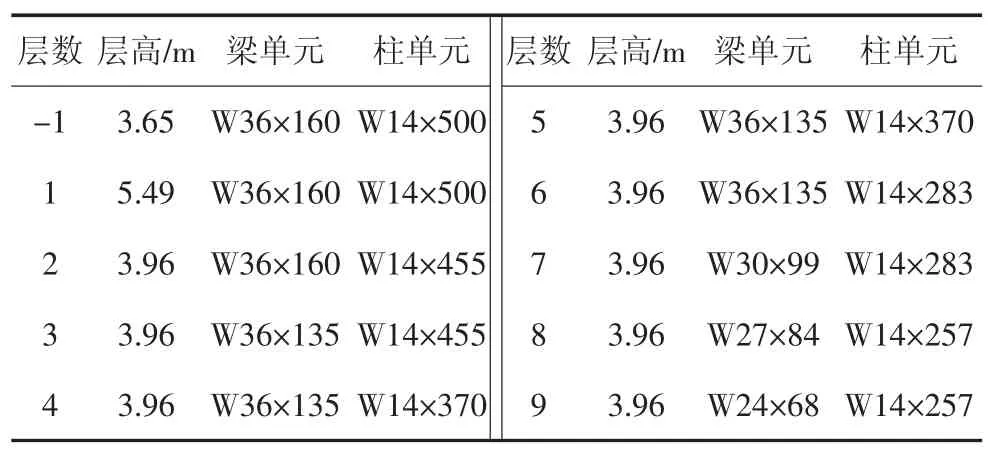
表1 9 层钢框架模型的构件尺寸Tab.1 Nine-layer steel frame model member dimensions

梁和柱单元塑性铰定义为SAP2000 中基于FEMA365 中的默认铰属性的集中塑性铰模型.其中柱单元采用的是考虑弯矩和轴力相互作用的P-M2-M3 耦合塑性铰，梁单元采用的是考虑弯矩的M3 铰，分别布置在梁柱0.1 倍和0.9 倍的长度位置处.图5为该9 层Benchmark 模型的三维框架立面及平面布置图，图6 为利用SAP2000 建立的有限元模型.

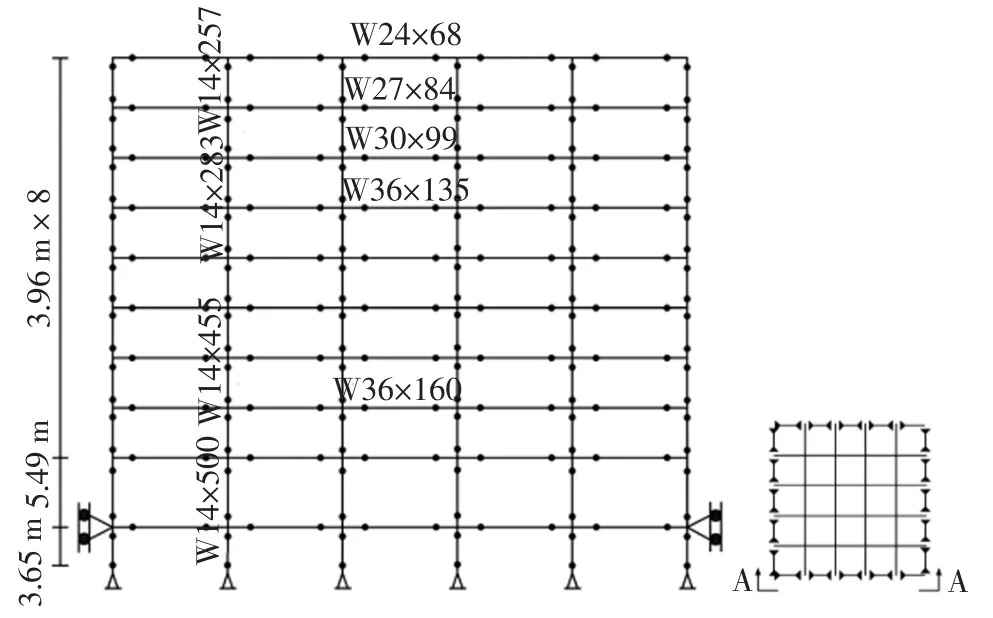
图5 9 层Benchmark 模型图Fig.5 9-story Benchmark model

图6 有限元模型Fig.6 Finite element model

1.2.3 火灾模拟模型创建

将该9 层Benchmark 建筑BIM 模型导出为fbx文件，并将导出的文件导入至Pyrosim 中，补充应有的信息并设置相应的参数可完成模型转换，图7为该9 层Benchmark 模型转换完成的火灾数值FDS 模型.

图7 火灾数值FDS 模型Fig.7 Fire numerical FDS model

2 地震后防火门破损评估分析

2.1 易损性数据

本文将利用基于FEMA P-58 来考虑震后门损伤对火灾的影响.在美国规范FEMA P-58 中提供了门这一非结构构件的易损性情况的数据，其中包含门的易损性曲线以及两种不同破坏程度的说明.表2为FEMA P-58 中提供的门易损性数据表.

表2 门易损性数据表Tab.2 Door vulnerability data sheet

图8 为FEMA P-58 中提供的门的易损性曲线，将其与地震损伤状态相关联，该曲线中包括两种不同的破坏状态分别为DS1 和DS2，其中横坐标为层间位移角数据，纵坐标为对应层间位移角下的损伤概率.DS1 指门受到一定程度的变形，导致门的开合受到影响，而当结构变形消失时，门的变形也随之消失，为弹性变形，据研究显示，一般发生于层间位移角为0.001 左右时；而DS2 指门受到不可自行恢复的损伤且需要修理，据研究显示，一般发生于层间位移角为0.004～0.01 时.

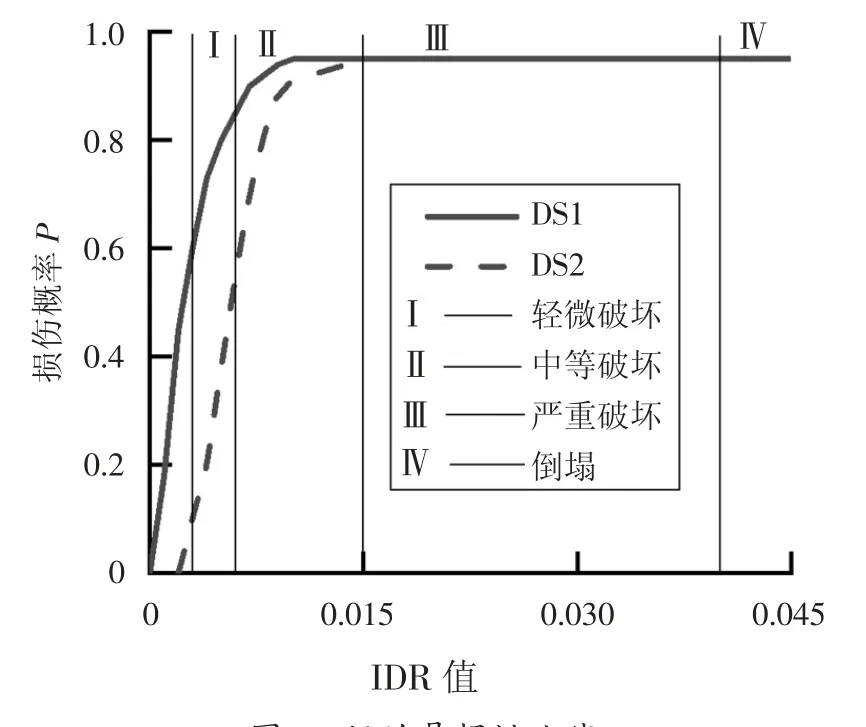
图8 门的易损性曲线Fig.8 Door vulnerability curve

2.2 门损伤模型

2.2.1 门损伤概率模型

本文选取9 层Benchmark 三维框架模型，以最大层间位移角θmax作为结构的损伤判定指标，利用王海东等[14]结合我国抗震规范及美国HAZUS[15]耐震规范中对不同损伤的定义划分.对应于FEMA P-58 提供的门的易损性曲线，由于4 种损伤状态下结构均已处于结构非线性阶段，故选用DS2 为门损伤状态计算其门损伤概率.表3 为结合门的易损性曲线及各破坏阶段下对应的层间位移角限值，得出在不同损伤状态下建筑内门的整体损伤概率.

表3 门的损伤概率Tab.3 Door damage probability

2.2.2 门损伤评估

采用非线性评估理论，依照Memari 等[16]在研究过程中选取的地震波，并参考我国《建筑抗震设计规范》的标准，选取表4 中3 条场地类型为Ⅱ类，参照之前学者研究成果[17]，依照震中距及震级得出各地震波的相应设计分组，以便工程应用.

表4 地震记录集Tab.4 Earthquake records

将以上选取的3 条地震波按规范要求，做最大值归一化处理，按照抗震设防烈度为8 度（0.20g）的罕遇地震情况，取PGA=0.4g 进行调幅.作用于9 层Benchmark 三维框架模型中进行非线性结构分析，以各层的层间位移角这一结构评估值作为非结构构件门损伤的评估指数.表5 为最终得出的在各地震记录影响下模型各层层间位移角的平均值及层占比，从而得出建筑模型下，在不同损伤状态时，各层门的损伤情况.

表5 层间位移角平均值及层占比Tab.5 Average value and layer proportion（IDRs）

2.2.3 9 层Benchmark 门损伤模型

该建筑火源信息模型中，门总数为289 樘，其中每层防火门为11 樘，其他为普通门，各层防火门位置一致，一层防火门位置如图9 所示，其中防火门1-1～1-7 防火门尺寸均为M1521，1-8～1-11 均为M1821.依照前文所述，将选取的地震记录作用于该建筑的有限元模型中，得到各层平均层间位移角并进行层占比计算.通过门的易损性曲线对应各状态下门的损伤比例，得出不同状态下各层门损伤数量，从而得出该模型的门损伤模型，表6 为地震记录下，结构不同损伤状态时各层门损伤数量.

表6 各层门损伤数量（樘）Tab.6 Number of damaged door

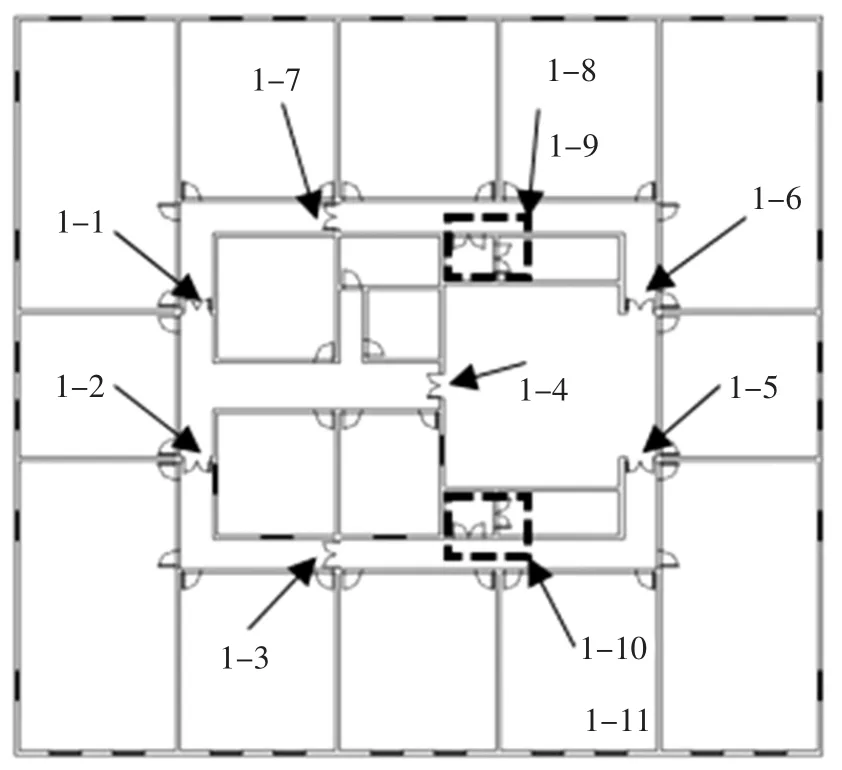
图9 防火门位置Fig.9 Fire door position

其中，当结构处于严重破坏及倒塌状态时，门的损伤概率已到达100%，则门损伤数量不依照各层层间位移角平均值的层占比分布，故不考虑.而结构在中等破坏状态下，考虑最不利布置原则，由于各层门损伤数量均大于11 樘（各层防火门数量），则最不利情况为各层防火门均损伤，此时各层火灾均蔓延至各防火分区，均已达最不利状态，故本文不考虑.

本文后续将考虑在结构轻微破坏下建筑的火灾模拟分析，并考虑最不利布置原则，将建筑模型中各层损伤的门均设置为防火门，由此更大程度地扩大室内火灾区域，从而考虑各种火灾发生的最不利情况.

3 火灾模拟分析

本文以结构在轻微破坏状态下为例，利用PyroSim 火灾模拟软件，分别将有无门损伤两种情况对火灾的影响进行模拟实验，模拟时间取为500 s.由于同层门损伤状态下发生火灾，对其他层温度的影响较小，故对各层分别进行模拟实验.本文选取模型的1 层、5 层及9 层为模拟层数，得出最低、正中间层、最高层各柱处最高温度曲线.

3.1 火灾场景设置

图10 中所示的起火点区域位于①防火分区（见图11），该区域在建筑设计中设置了茶水间，内有大功率用电设备，且与各防火分区均有接触面，当防火门损伤时，火灾具有最大的扩散面积，为最不利，且图10 表示各层考虑门未损伤时的火灾场景.图11为各层柱编号所对应框架柱所在位置及防火分区.同时，由于该建筑功能为办公楼，考虑反应过程、燃烧产物等因素，设定与现实场景相符的起火场景及相应的化学反应.本文则根据办公室的起火特性，选取办公室标准的Polyurethane GM37（聚氨酯）反应起火.由于办公楼可能存在大量的沙发坐垫以及可能存放的纸箱，依据最不利原则，设定火灾为快速增长型，火灾增长系数α 取0.046 89，火源最大热释放速率为1 000.0 kW，按照t2火模型计算得到火灾到达最大速率的时间为146 s，在本文中，由于设置的燃烧物有限，模拟火灾过程影响，发现各柱在500 s 内均已达到火灾温度下降段，故选取该模型模拟时间为500 s.

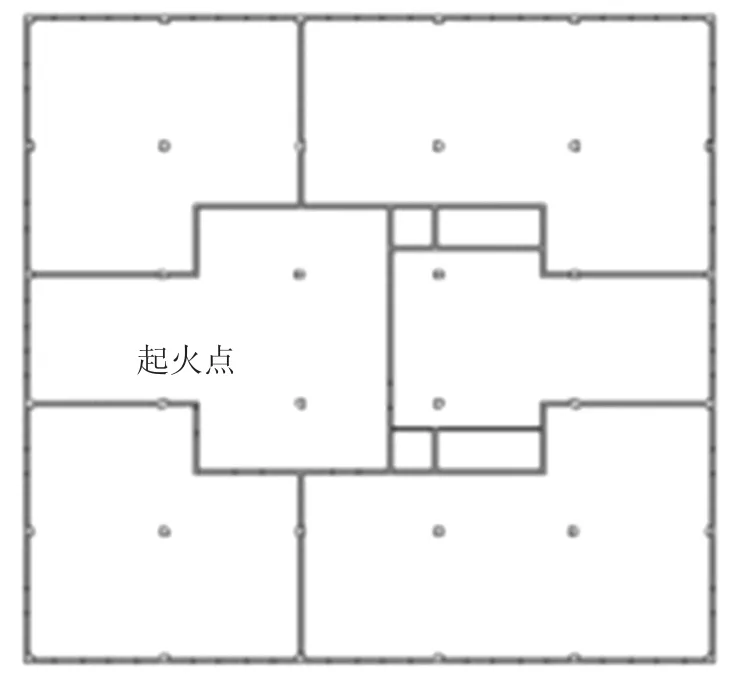
图10 起火点位置信息图Fig.10 Fire location information

图11 框架柱位置及防火分区Fig.11 Frame column position and fire compartment

本文主要研究该模型结构在轻微破坏下，1、5、9层在有无考虑门损伤状态两种情况下对结构温度的影响.由前文可知，5 层门损伤的数量为3，1、9 层门损伤数量为4，由此进行模拟计算.

由于1、5、9 层的门损伤数量以平面视角分类，则共有2 种损伤类型，分别为门损伤数量为3 和4.考虑火灾现场设计的最不利原则，应将损伤的防火门设置在火源物质影响更大的位置处，故选择图12、图13 所示的设置方式，门损伤数量分别为3 和4.

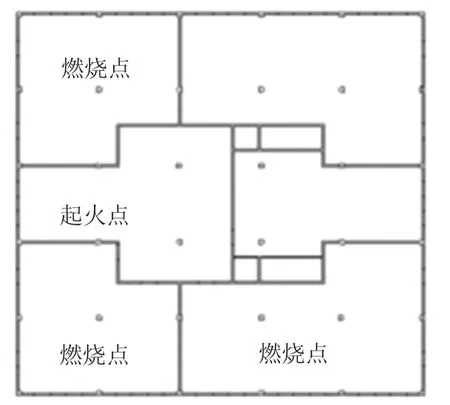
图12 火灾场景——3 防火门损伤Fig.12 Fire scenario——3 damaged fire door

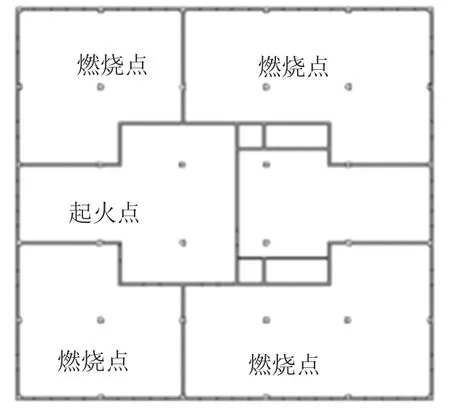
图13 火灾场景——4 防火门损伤Fig.13 Fire scenario——4 damaged fire door

3.2 温度数据

在以上火灾模拟中，共有6 种工况，分别为工况1：9 层4 防火门损伤；工况2：9 层门未损伤；工况3：5 层3 防火门损伤；工况4：5 层门未损伤；工况5：1层4 防火门损伤；工况6：1 层门未损伤.由于模型中各层框架柱共计36 个，模拟500 s 内各层柱中部温度变化情况，并记录其最高温度，按各防火分区进行统计，分别得出图14～图19 各防火分区6 种不同工况的最高温度情况，表7 为各防火分区内包含的柱编号.

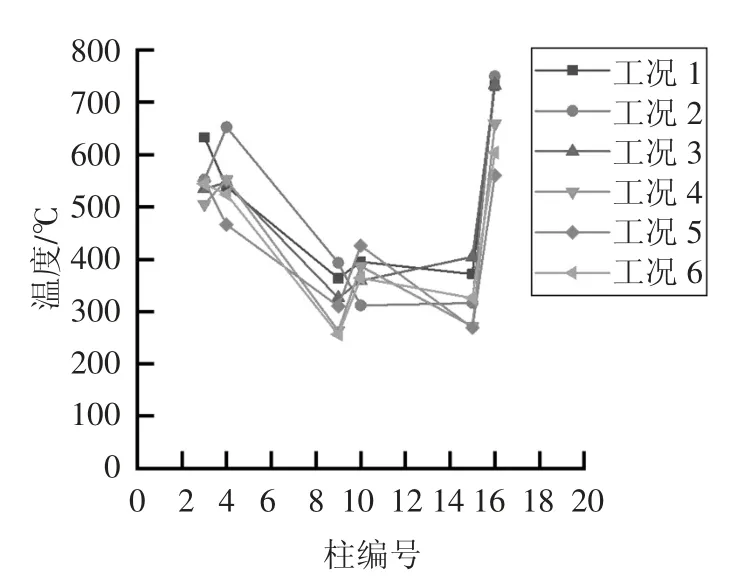
图14 第一防火分区柱温度Fig.14 Column temperature in the No.1 fire compartment

图15 第二防火分区柱温度Fig.15 Column temperature in the No.2 fire compartment

图16 第三防火分区柱温度Fig.16 Column temperature in the No.3 fire compartment

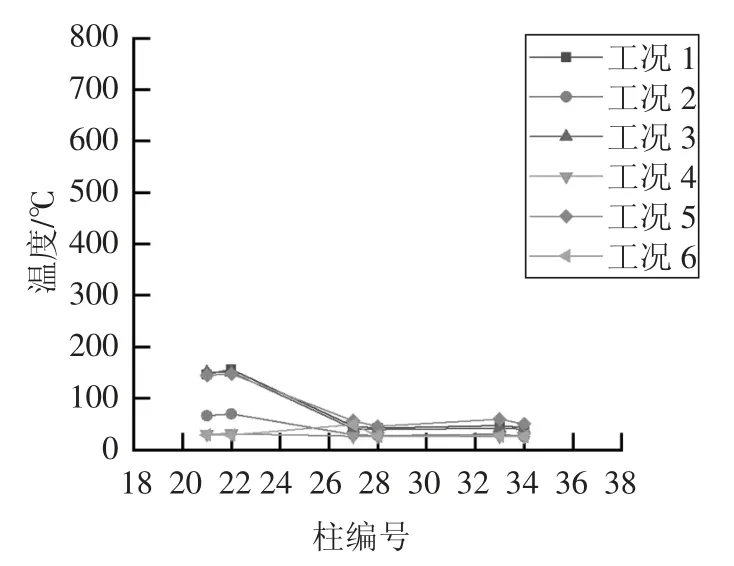
图17 第四防火分区柱温度Fig.17 Column temperature in the No.4 fire compartment

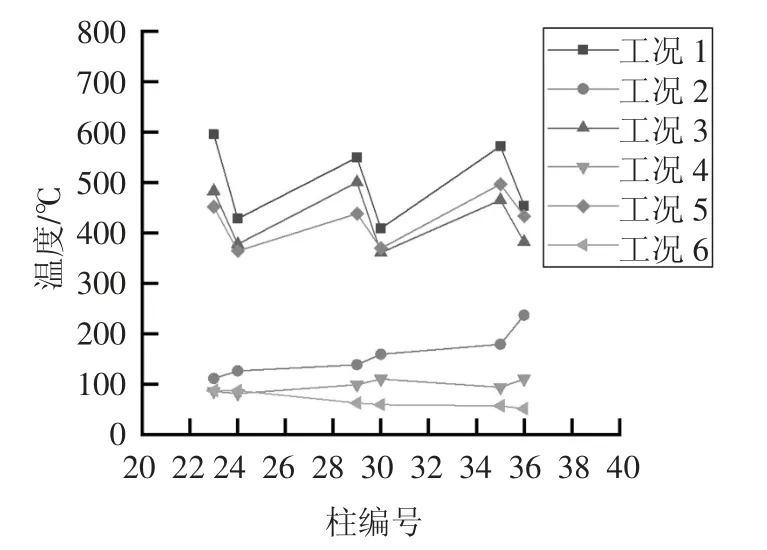
图18 第五防火分区柱温度Fig.18 Column temperature in the No.5 fire compartment

表7 防火分区内柱编号Tab.7 Columns number in fire compartment

3.3 模拟结果分析

由各层柱在6 种工况、不同门损伤情况下统计得到的最高温度可知，门损伤数量的增多将对框架柱温度有直接影响，且门损伤数量越多，框架柱温度越高.统计可得，在火灾模拟500 s 内，当框架柱最高温度高于300 ℃时，则100 s 内基本达到构件的最高温度；当框架柱最高温度低于300 ℃时，则在模拟时间为300 s 后基本达到构件的最高温度.

通过统计各工况下各框架柱的最高温度可知：框架柱位于着火点及在所有工况下均未燃烧的防火分区时，考虑地震作用和未考虑地震作用的框架柱燃烧温度基本吻合；而框架柱位于其他燃烧点的防火分区时，未考虑地震作用下门损伤情况的燃烧温度将明显低于考虑地震作用下门损伤情况的燃烧温度.且以本文1、5、9 层对应考虑地震作用与未考虑地震作用的所有工况下，统计可得考虑门损与未考虑门损的框架柱温度差值最大达483.98 ℃，该点为9 层23 号柱.

根据《建筑钢结构防火技术规范》[18]可知，当温度达到300 ℃以上时钢材的屈服强度将进行折减，故本文以计算屈服强度折减系数为1.0、0.95、0.9 时钢材的温度作为统计边界值，分别为300 ℃、375 ℃、409 ℃.图20 为统计各工况下框架柱最高温度达到该三者统计边界值以上的数量，为后续分析温度对柱承载能力的影响提供基础.且由各框架柱最高温度的统计结果可知，考虑地震作用门损伤时达到边界温度值的框架柱数量比不考虑地震作用门损伤时多达4.25～7.33 倍；当考虑门损伤情况下，框架柱温度及达到统计边界值的数量排序均为：9 层＞1 层＞5层；当不考虑门损伤的情况下各层达统计边界值数量趋于稳定.

图20 达各边界温度值的框架柱数量统计（300 ℃、375 ℃、409 ℃）Fig.20 The number of frame columns reaching the temperature of each boundary（300 ℃，375 ℃，409 ℃）

4 结论

本文利用BIM 技术和FEMA P-58 提出了一种基于性能的考虑非结构构件破损的震后次生火灾模拟方法，定量评估由于门损伤对火灾温度场的影响，并反映于框架柱的温度，相关结论如下.

1）提出了基于BIM 的建筑火源信息模型，并将其作为信息传递中心，将结构模型与火灾模型相结合.

2）将地震作用下的层间位移角与非结构构件门的易损性进行关联：

①当结构处于严重破坏或倒塌状态时，各层门损伤概率达100%，此时震后火灾温度场与防火门无关；

②当结构处于中等破坏时，门损伤概率为56%，此时各门为有概率的损伤，若考虑最不利情况为防火门全数损伤，火灾蔓延至全部防火分区，将达到火灾最不利影响；

③在结构处于轻微破坏时，门损伤的概率为10%，防火门是否损伤具有随机性，考虑地震作用下防火门损伤情况对震后火灾温度场分布具有显著的影响，故在中低地震设防区具有重要意义.

3）当结构处于轻微破坏时，通过对比6 种工况下各框架柱的温度变化情况及最高温度统计可得：

①当框架柱位于非着火点及引燃的防火分区时，未考虑地震作用门损伤的燃烧温度将明显低于考虑地震作用门损伤的燃烧温度，且框架柱温度差值最大为483.98 ℃；

②通过统计钢材屈服强度折减系数为1.0、0.95、0.9 所对应的边界温度值300 ℃、375 ℃、409 ℃的框架柱数量可知，考虑门损时达到边界温度值的框架柱数量将远远高于未考虑地震作用门损时的框架柱数量，其比值最高可达7.33 倍；

③达统计边界值的数量具有差异但有一定规律性，在考虑地震作用门损伤时，各层达统计边界值数量为9 层＞1 层＞5 层.未考虑地震作用门损伤时，各层达统计边界值数量趋于稳定.