砂土中吸力式三筒基础水平承载特性试验研究
赵学亮,李扬扬,王鑫,朱文波,戴国亮,邓温妮
(1.东南大学 土木工程学院,江苏 南京 211189;2.混凝土及预应力混凝土结构教育部重点实验室(东南大学),江苏 南京 211189;3.林同棪国际工程咨询(中国)有限公司,江苏 南京 210019)
吸力式三筒导管架基础作为一种新型深水基础结构型式,弥补了单桩基础与重力式等传统基础结构导致工程造价过高、经济效益低等缺点,在海上风电工程中的应用逐渐增多.吸力式三筒基础主要承受风、浪产生的水平力以及传递到基础的弯矩作用[1-2],其中筒间距、长径比与加载方向对三筒基础水平承载力影响较大.因此,对新型海上风电吸力式多筒导管架基础结构在水平及弯矩共同作用下的承载特性进行试验研究具有重要的理论和实践意义.
目前关于吸力式筒型基础水平承载特性已有不少相关研究成果.Bransby 和Randolph[3]对粉土地基中单筒基础进行V、H、M 复合加载条件下的小比例尺室内模型试验研究.试验探讨了不排水加载和部分排水加载条件下筒基础承载力变化情况.Wakil[4]通过离心机室内试验研究了不同砂土密实度下圆柱形单筒基础水平承载特性,得到了密实度与承载力之间的影响规律.Kim 等[5]通过试验对粉砂地基中三筒基础在水平荷载作用下的力学特性进行研究,试验结果与单筒进行对比,发现三筒基础有更好的抗倾覆能力.张苇[6]通过模型试验研究了吸力式三桩基础在水平与竖向组合荷载作用下,长径比、荷载作用角度及桩间距等因素对承载特性的影响规律.还有学者通过理论与有限元方法研究了吸力式筒型基础的水平极限承载力.刘振纹等[7]利用模型试验结果,探讨了水平荷载下单筒基础的破坏模式,以极限平衡法中Engel 假设为基础,分析水平荷载下单筒的受力状态,推导出单筒基础水平极限承载力理论公式.Bang 等[8]通过离心机试验研究了不同荷载作用点和作用角度下砂土地基中吸力式沉箱基础的抗拔承载力.黎冰等[9-10]通过一系列模型试验研究了吸力式沉箱基础的最佳作用点位置,试验中考虑了荷载作用点、荷载作用角度和长径比3 个重要因素.结合荷载与吸力式沉箱基础的转角关系,分析了荷载水平作用于最佳作用点下吸力式沉箱基础的破坏模式.Gourvenec[11]通过有限元模拟了单筒基础在非均质黏土中复合加载模式下受力状态,分析了基础长径比与地基承载力包络线形状之间的关系.
综上可以发现,目前筒型基础研究成果很多集中在单筒基础的力学特性分析,针对砂土地基中的多筒基础的受力特性,尤其是试验方面的研究尚不充分,本文考虑吸力式三筒基础不同长径比、水平荷载角度和筒间距,通过模型试验和数值模拟对砂土中吸力式三筒基础水平承载特性进行研究.
1 试验内容与试验方法
为了研究砂土地基中吸力式三筒基础的水平承载力特性,试验中考虑了3 种不同长径比筒基础、3个荷载作用方向和3 个筒间距,共13 组工况(每组工况中,三筒基础的3 个筒大小相同),模型试验方案如表1 所示.

表1 试验工况汇总表Tab.1 Test programs
为保证模型周围土体满足消除边界效应的要求,模型箱尺寸(长×宽×高)为1.2 m×1.2 m×1.5 m.模型槽采用单面排水,具体做法为铺排出水孔径8 mm 排水管网于模型箱底部[12],由于地基土为砂土,在排水管上铺设一层土工布,防止排水过程中有砂砾排出,土工布上方布置150 mm 厚的碎石反滤层,其上再铺设一层土工布增强过滤与排水效果.通过颗粒级配试验所得的土样级配曲线如图1 所示.模型箱内铺设砂土总厚度为1.45 m,采用分层铺设,每层厚度约为0.2 m,并用夯锤人工夯实,满夯20 遍.砂土铺设完成后对其注水至与土样表面齐平,静置1 d 进行固结[13].固结完成后,取箱内10 cm 以下土样,按照《土工试验方法标准》(GB/T 50123—2019)进行室内土工试验,测得试验砂土的基本物理力学性质见表2,本试验用砂相对密实度为0.59.

图1 颗粒级配曲线Fig.1 Grain size distribution curve

表2 试验用砂物理参数Tab.2 Physical parameters of sand
试验中的模型筒采用Q235 钢管,外径分布为102 mm、120 mm 和133 mm 3 种,对应的筒身长分别为164.7 mm、134 mm 和112.6 mm,壁厚为3 mm,每种尺寸的筒重量相同,均为1.45 kg.单筒顶部预留两个螺栓孔,一个用于与筒顶部三脚架相连接,另一个作为排气孔方便筒的贯入与拔出,如图2 所示.筒顶三脚架中部位置留出长度为150 mm 螺栓孔,方便调整筒与筒之间的位置来研究三筒筒间距对三筒基础承载力影响.其次,在三脚架每隔90 mm 处设置一吊耳用于三筒基础施加水平荷载,三筒结构示意图如图3 所示.三筒基础呈等边三角形结构布置,

图2 筒型基础单筒模型示意图Fig.2 Schematic diagram of single caisson model

图3 组合三筒模型示意图Fig.3 Schematic diagram of tripod-bucket foundation
根据结构的对称性研究荷载的方向只需要在0°到60°范围内进行,如图4 所示.

图4 加载方向示意图Fig.4 Schematic diagram of load direction
相关研究表明[14-15],下沉方法对吸力筒基础长期承载力的影响很小,针对本文小比尺模型采用负压和重力共同贯入的方法,利用垂直贯入装置将沉箱模型完全沉入试验土池中,使筒顶面与泥面齐平.筒基础贯入24 h 后,通过分级加载法施加水平荷载,荷载级差取预估荷载的1/10[16].如图5 所示,水平荷载通过砝码、加载架和滑轮进行施加,试验过程中,通过在筒顶处设置的位移传感器记录测量点的水平位移,具体的试验示意图如图5 所示.

图5 模型试验示意图Fig.5 Schematic diagram of model test
2 试验结果分析
目前对于吸力式三筒基础水平极限承载力,国际上还没有统一的破坏标准,也缺乏相应的位移特征点研究结果.由于三筒基础目前应用相对较少,更缺乏有关三筒基础的破坏标准.作者对目前采用的一些极限承载力的确定方法进行了总结,本文对于吸力式三筒基础水平极限承载力判断主要方法是通过荷载-位移曲线上特征点的角度对基础水平承载力进行判定,针对具有明显拐点的曲线选取拐点值为特征点,对没有明显拐点的曲线采用切线相交法[16]选取特征点.
2.1 长径比对承载力影响
选取两组不同筒间距(S/D=2.0 和S/D=3.0)在相同荷载作用角度下的工况,分析长径比对水平承载力的影响.图6 分别给出了相同筒重、不同三筒尺寸条件下,筒间距S/D=2.0 和S/D=3.0 在0°荷载作用方向工况下的荷载-位移曲线.由图6(a)可知,当三筒基础各个筒之间的距离为3 倍筒径时,不同尺寸的单筒对组合三筒基础结构水平承载力的影响较为明显,长径比L/D=1.61 的基础水平承载力最大,L/D=1.12 下基础水平承载力次之,L/D=0.85 时基础水平承载力为最小.进一步分析筒间距为2 倍筒径时结果,由图6(b)可知,当S=2D 时所得结论与S=3D 基本一致.

图6 不同S/D 和L/D 三筒基础的荷载-位移曲线Fig.6 Load-displacement curves with different S/D and L/D
图7 给出了不同筒间距情况下,三筒基础的水平极限承载力与长径比之间的关系.从图中可以发现当筒间距S/D=2.0 时3 种长径比下的基础水平承载力差距不大;但当筒间距S/D=3.0 时,各长径比下的水平承载力相差较为明显.这是由于当筒间距较小时,各个筒之间的相互影响明显,三筒基础工作状态类似于大直径单筒,削弱了长径比变化对整体水平承载力的影响.这一现象可从相同工况下有限元模拟结果(图8)进一步进行阐明.从图8 中可以看出,在同为S/D=3.0 条件下,长径比L/D=1.61 的三筒基础筒之间的相互影响最为突出,长径比较小的两组筒基础(L/D=1.12 和L/D=0.85),虽然筒间距相对值S/D 相等,但由于它们筒间距绝对值较L/D=1.61 更大,筒之间的影响较小.当筒间距较大时,三筒基础结构的各个筒之间联系减弱,相互影响作用减小,其工作状态类似于三个单个筒的叠加作用,此时水平极限承载力主要受长径比的影响,长径比越大的筒其侧摩阻力越大,抗拔能力越强,故长径比大的L/D=1.61 的三筒基础水平承载力显著提高.

图7 水平承载力随长径比的变化关系Fig.7 The relationship between the horizontal bearing capacity and length diameter ratios


图8 不同长径比下基础浅埋层地基表面位移Fig.8 Shallow surface displacement of foundation under different aspect ratios
2.2 荷载作用方向对承载力影响
当筒间距S/D=3.0 时,分析长径比分别为L/D=1.61 和L/D=1.12 下荷载作用角度与承载力之间关系.图9 为三筒基础在不同水平荷载作用方向下,承载力随着水平位移的变化结果.从图9 中可以看出,三筒基础的水平极限承载力受荷载作用方向的影响较为明显.两种不同长径比的工况均在0°方向下三筒基础水平承载力为最大,而60°方向下,基础的水平承载力为最小.但图9(a)中,0°方向下长径比L/D=1.61 的三筒基础在加载过程中其水平位移大于其他两种工况,造成这种现象的原因是在该组试验中,加载时荷载级差取值较小,为预估值的1/20,因此累积变形的次数和时间增多,相应的变形更大.
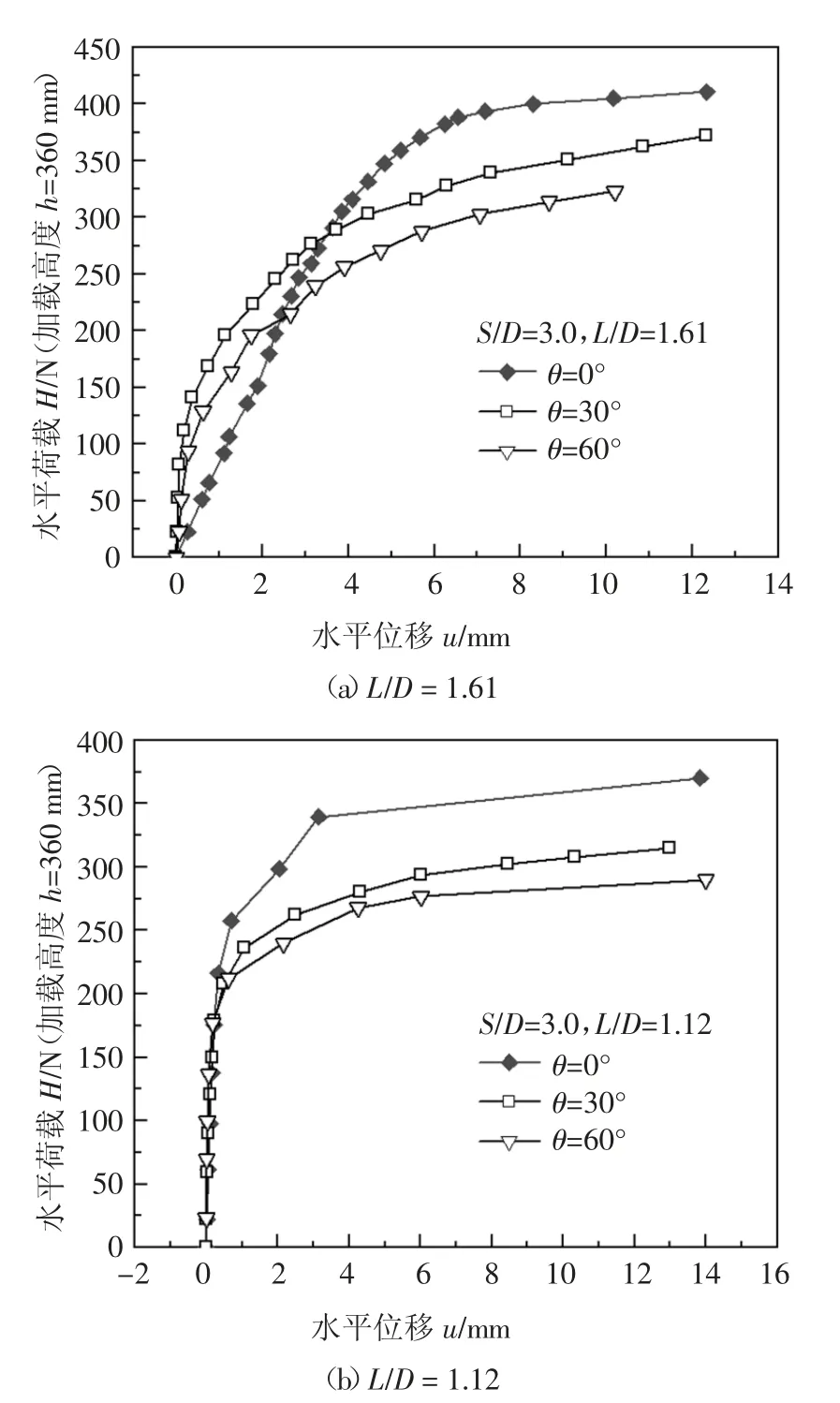
图9 不同L/D 和加载方向荷载-位移曲线Fig.9 Load-displacement curves with different L/D and loading direction
图10 给出了不同模型尺寸情况下,三筒基础的水平承载力随着荷载作用方向变化的结果.从图10可知,三筒基础的水平承载力随荷载作用角度的增大而降低,0°方向下基础承载力最优.分析原因为:对于吸力式三筒基础结构型式,筒与筒间土相互作用区域将影响联合工作效果的发挥,筒-土之间联合工作效果随荷载作用方向的改变而发生变化.当荷载角度为0°时,三筒基础筒-土间联合工作影响的范围相对较大,联合工作效果明显;当荷载角度为60°时,联合工作区域最薄弱.除联合工作效应的影响以外,三筒基础水平承载力也受位移的影响.三筒基础的整体位移大小取决于结构最薄弱环节产生的位移,当荷载作用角度为0°时,此时失稳状态为一个筒受压,两个筒受拉,产生位移最大处取决于受压筒;当角度为60°时,一个筒受拉,两个筒受压,最薄弱环节位于受拉筒,由于筒的抗压承载能力要远大于抗拔承载能力,因此三筒基础在0°荷载作用方向下承载力要大于60°下承载力.

图10 水平承载力随荷载作用方向的变化关系Fig.10 The relationship between the horizontal bearing capacity and loading directions
2.3 筒间距对承载力影响
图11 为长径比分别为L/D=1.61、L/D=1.12、L/D=0.85 情况下不同筒间距吸力式三筒基础水平承载力与位移的关系曲线.从图11 可看出,随着三筒基础筒间距增加,相同水平和弯矩荷载作用方向下水平极限承载力总体呈现增长趋势,主要原因为随着筒间距增大,筒之间的干扰减弱以及筒基础力矩臂增加提高了极限承载力.但在长径比L/D=0.85情况下有所不同,三筒基础水平极限承载力并没有有随筒间距增大而一直增加,这是由于长径比较小的三筒基础,由于本身筒长较小,影响的筒周围的土体范围也较小,在其筒间距达到某一长度时,筒与筒之间的相互联系非常弱,各个筒单独工作.
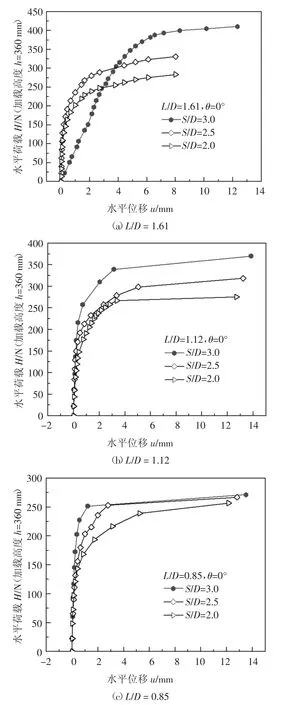
图11 不同L/D 和S/D 荷载-位移曲线Fig.11 Load-displacement curves of tripod-bucket foundation with different L/D and S/D
由于吸力式三筒基础通过支撑架与上部结构连接,筒间距大小直接影响支撑架尺寸从而影响结构整体用钢量,因此可在本次试验结果的基础上研究如何在满足基础承载力的同时,从用钢量出发优化基础长径比及筒间距.采用目前应用最广泛的基础结构型式作为计算样本,如图12 所示,横撑与斜撑之间夹角均为60°.基于本文所研究的筒不属于大直径筒基础范畴,为了简化计算,参照一些学者的研究结论和规范建议以及一些实际工程经验,横撑与斜撑的直径均取0.75 倍的筒基础直径,横撑与斜撑的壁厚取0.02 倍的直径大小.计算不同筒间距和长径比下筒基础上部与连接段的支撑架的用钢量及承载力,并作对比分析,具体计算结果见表3.
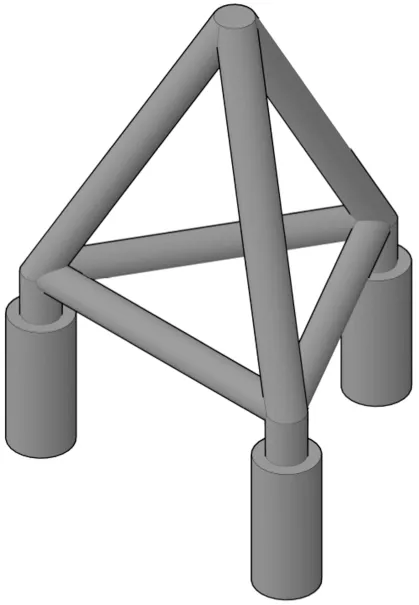
图12 吸力式三筒基础结构型式Fig.12 The structure type of tripod-bucket foundation

表3 吸力式三筒基础结构用钢量与水平承载力增长率结果Tab.3 Results of steel consumption and growth rate of horizontal bearing capacity of tripod-bucket foundation
通过表3 可知,对于L/D=1.61 和1.12 两种情况下的三筒基础,当筒间距S/D 从2.5 增加到3.0时,其水平极限承载力增长率最大,此时增大筒间距对提升水平极限承载力的效果最明显,对于长径比小于1 的浅埋吸力式三筒基础,其筒间距S/D 值推荐为2.0 或2.5.
2.4 三筒基础的失稳破坏机制
三筒基础在水平力作用下破坏模式主要表现为受压筒前后侧土体发生塑性破坏,受拉筒被拔出泥面.图13 为水平荷载作用下三筒基础逐渐失稳破坏的过程,可以分为3 个阶段.

图13 三筒基础试验过程Fig.13 Test process of tripod-bucket foundation
结合图6、图9、图11 三筒基础水平承载力结果与图14 基础逐渐失稳视图可以发现,在试验初始阶段到试验中间阶段,三筒基础只出现微小的水平位移,筒周围土体仍处于弹性变形阶段,模型实验中很难观察到明显的变形,只在受拉筒后侧出现狭窄的微裂缝,此时的受压筒周围土体几乎没有出现变形;随着加载继续,筒周土体由弹性变形阶段逐渐进入塑性变形阶段,受拉筒后侧出现的裂纹随着荷载的增大逐渐向后方扩展,受拉筒前侧土体出现隆起趋势,受拉筒发生向上拔起的趋势并向加荷方向旋转,此时受压筒后侧的裂缝可以观察清楚,但受拉筒周围土体的变形要明显大于受压筒周围的土体.

图14 三筒基础逐渐失稳过程Fig.14 Failure of tripod-bucket foundation before and after instability
当荷载达到一定值后,荷载难以继续施加,通过位移计显示结果来看,筒基础的水平位移持续并急剧增大,整个基础进入完全失稳阶段.观察筒周围破坏土体发现,受拉筒前后侧的土体发生的塑性破坏仅限于靠近土体表面那一层,且随着长径比的减小,发生塑性破坏的土层越薄,说明受拉筒主要做上拔运动,如图15 所示.受拉筒在被拔起时,筒内土塞发生脱落,筒内壁与土塞存在摩擦,这表明受拉筒提供的水平抗力主要来自筒壁内外侧与砂土之间的摩擦力;受压筒前侧土体则受挤压逐渐隆起形成被动侧破坏楔体,且破坏范围广、深度大,筒体前侧的被动区土压力也提供了三筒基础水平抗力.
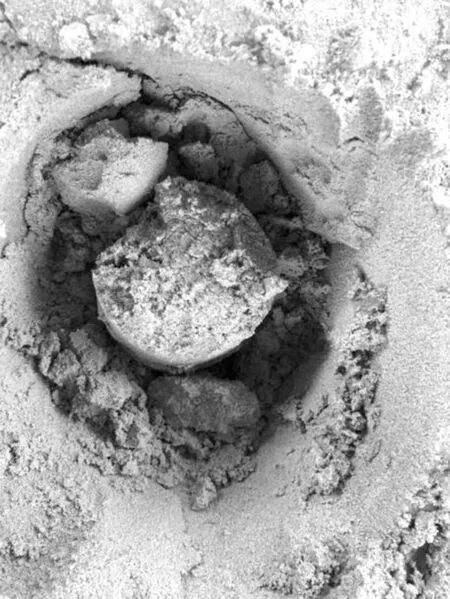
图15 受拉筒内土塞脱落Fig.15 Soil plug falling off tension cylinder
图16~图18 分别是通过有限元软件PLAXIS模拟筒间距S/D=3.0、加载方向0°、高度H=360 mm 时,长径比分别为L/D=1.61、1.12、0.85 的3 个工况下得到的位移矢量图、三筒基础整体变形云图以及受压筒位移结果.
从图中可以看出:1)水平荷载作用下当筒的长径比较小时,受压筒水平运动占比较大,受拉筒主要是垂直上拔,这也解释了模型试验中长径比越小,受拉筒前后侧发生塑性破坏的土体越小这一现象;随着筒裙高度增加,受压筒转动趋势愈加明显,同时也有少量水平位移,受拉筒在上拔过程中会伴随前倾的转动趋势,如图16 所示.根据三筒基础整体变形云图(图17)可以判断,受压筒前会受到很大的压应力作用,上部会首先出现塑性破坏并不断扩展.三筒基础的水平抗力主要来自于两个受拉筒的筒壁摩阻力以及受压筒前侧土体提供的压应力.2)由图中受压筒位移云图(图18)变化趋势可以看出三筒基础围绕受压筒底部转动,与单筒基础在水平荷载作用下的转动中心的位置相一致,有所不同的是,单筒基础在水平力作用下其转动中心在筒的中轴线上,而三筒基础的转动中心在受压筒中轴线偏向水平力方向一侧的位置,并且转动中心在Y 方向的位置随着长径比的改变变化不大,而转动中心在Z 方向的位置随着长径比的减小而降低.这个趋势也很好地解释了长径比大的筒在水平力作用下转动占主要变形,长径比小的筒主要变形为水平位移.

图16 有限元计算位移矢量图Fig.16 Displacement vector diagram calculated by finite element method

图18 三筒基础受压筒位移图Fig.18 Displacement diagram of compressed cylinde
3 结论
通过模型试验研究了砂土中吸力式三筒导管架基础的水平承载特性,结论如下.
1)三筒基础在水平荷载作用下,基础失稳模式表现为:加载前期,基础伴随着平动加转动的趋势,长径比大的基础其转动趋势更明显,长径比较小的结构其平动趋势更明显,但最终的破坏形式都表现为倾覆破坏.三筒基础整体结构转动中心位于受压筒中轴线附近,长径比越小,转动中心在深度方向上位置越低.由于转动中心在受压筒内,受压筒周围土体变形最明显,土压力值明显大于其他区域.在水平荷载作用下,基础围绕某一点发生转动,转动轴以上土前侧土体为被动区,被动区土体刚度相比于基础结构很小,因此,当基础失稳时,在被动区一侧会产生很大的剪切变形.受压筒前侧土体拱起,形成被动破坏区,而筒后筒-土分离形成裂缝.这种基础失稳的主要原因是由于被动区土压力过大而产生土体塑性破坏.
2)水平荷载作用下,当基础长径比较小,在位移较小时就发生整体倾覆破坏;在长径比较大时,基础发生倾覆前会经历较大程度的位移变化.这些规律可为确定吸力式三筒基础破坏标准做参考.受拉筒前后侧土压力值较小,说明受拉筒主要作上拔运动,筒内外侧与土体的摩阻力是提供三筒基础水平承载力的主要抵抗力.
3)相同筒重条件下,长径比大小对三筒基础水平承载力的影响明显,特别是在筒间距较大的情况下,长径比这一影响特点更明显.
4)同一筒间距下,荷载作用方向对吸力式三筒基础水平承载力影响显著.荷载最有利方向为0°,此时对应的联合工作效应区域最大;最不利方向为60°,此时筒-土间的联合工作效应最弱.
5)相同尺寸和荷载方向条件下,随着筒间距的增加,承载力有不同程度的提升,长径比越大,承载力增幅越明显;当长径比较小时,承载力随着筒间距的增大而略微增加,并在某个筒间距范围内达到稳定值.

