深度学习在实测沉降数据预处理中的应用研究
胡安峰,李唐,陈缘,葛红斌,李怡君
(1.浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310058;2.浙江大学 平衡建筑研究中心,浙江 杭州 310058;3.浙江大学 建筑设计研究院有限公司,浙江 杭州 310058;4.厦门翔业集团有限公司,福建 厦门 361012)
作为岩土工程的经典问题,预测地基的沉降过程是尚未完全解决的难题.传统预测沉降的方法一般有三种:一是利用沉降的理论计算法,如各类分层总和法与固结理论[1-4],但由于难以获取原状土参数以及施工现场的复杂性,计算出的结果往往和实际有一定差距.二是有限元建模等数值方法[5-9],除上述原状土体参数问题外,有限元法还存在模型参数选取偏经验化,迭代过程复杂耗时,易出现奇异点等多种问题,计算出的结果和实测值相比也不够准确.与上述两种方法相比,第三种的曲线拟合法通过实测数据来推算沉降量与时间的对应关系,能更真实地反映地基的沉降规律[10].应用广泛的有指数曲线法[11]、双曲线法[12]、泊松法[13]和Asaoka 法[14]等.曲线拟合法是通过在实测曲线上采点来拟合曲线,从而预测后续的沉降.为保证后续沉降预测顺利进行,实测数据的准确度就变得至关重要.但在实际工程中,现场实测沉降数据常常存在诸多问题.
对于在建的大型地基处理项目,测点通常在千位数量级,由于人工误差、仪器误差等影响,一般很难保证所有测点数据都准确无误.为避免异常数据对后续沉降预测的干扰,在使用曲线拟合法或其他预测方法之前,存在对实测沉降数据进行遴选及预处理的需求.
深度学习是近年来进行数据处理的高效方法,在沉降预测等岩土领域中的应用也较多[15-24],但迄今为止,尚无文献研究过使用深度学习对沉降数据进行预处理.本文结合以上研究,提出了一种利用深度学习作为沉降数据预处理的新方法.由于深度学习是通过搭建神经网络来观察数据并发现其内在关联,因此对于数据的处理能力要明显优于其他方法[25-27].其中,长短期记忆网络LSTM[28-31]尤其擅长处理时间序列,这种带有记忆功能的神经网络,能自动地观察符合沉降发展规律的测点数据,学习良好的实测曲线具有的模式,然后将学到的映射关系应用到问题测点来重新计算全过程沉降值.
由于深度学习一般由多个处理层来组成计算模型,可学习具有多个抽象级别的数据表示[25],在经过若干处理层的转换之后,模型可以学到非精细的模式和特征[26].因此,本文基于深度学习中的长短期记忆网络LSTM,通过搭建Seq2Seq 模型[32-33],提出了对实测沉降数据进行预处理的新方法.在对比模型重新计算的全过程沉降值与对应的实测值后,验证了该数据预处理方法的可行性.最后,还对Seq2Seq 模型的超参数与数据情况等主要影响因素进行分析,探讨了模型的具体应用方法.
1 基于深度学习的沉降计算原理研究
如图1 所示,深度学习处理问题的出发点与传统思维完全不同.传统思维方法会事先建立从输入到输出的映射规则,而深度学习则首先通过输入与已知的输出标签来反向求解出这种映射关系,再对新的输入数据应用训练得到的模型来计算输出.

图1 深度学习的范式Fig.1 The paradigm of deep learning
对于沉降计算问题,根据沉降计算理论,不论是式(1)的普通分层总和法还是式(2)的建筑地基基础规范修正式,关键都在于经验系数簇α 的选取.

又对于式(3)太沙基一维固结理论,将其简化为式(4).若考虑非线性固结,则如式(5)(6)所示[34],按应力和应变定义的固结度存在差异.式(4)(5)(6)的重点在于函数簇f 的选取.因此,沉降计算在统计方法上可以看作对α 和f 分布的选取.

深度学习可通过多个处理层组成的神经网络模型,来学习沉降数据的发展规律,经过多个处理层的转换之后,理论上模型可以组合出任意函数分布[15].应用在沉降计算过程中时,网络参数会根据实测数据的输入(即土体参数)和答案(即实测沉降值),不断调整自身参数值,优化出最符合此现场沉降发展规律的α 和f 函数簇的分布.并且深度学习优化出的α 和f 可以随时间变化,表现出高度非线性,这也符合在不同沉降发展阶段,α 和f 应取不同值的理论依据.因而,深度学习契合沉降计算的要求.
深度学习最大的优势在于,除了经验系数α 和f的选取完全来自于对数据模式的高效识别外,还在最初就考虑了各种不可控噪声对沉降的影响.在数据量大的条件下,深度学习模型由于具有记忆和遗忘功能以及强大的学习能力,可以通过对多个良好测点沉降模式的学习来识别这些噪声,从而在异常数据处理时,除了经验系数之外还能考虑到噪声的影响.其中,处理沉降发展曲线这种时间序列尤其适合LSTM.
2 LSTM 与Seq2Seq 模型
2.1 LSTM 神经元内部结构
传统深度神经网络虽然能对数据进行逐层的特征提取,但无法考虑时间顺序,没有办法对时间序列进行有效的处理.循环神经网络RNN 正是为克服这个缺点而诞生的,也即RNN 拥有一定的记忆功能.具体的表现形式为循环神经网络会对前面的信息进行记忆并应用于当前输出的计算中,隐藏层之间的节点不再是无连接而是有连接的,并且隐藏层的输入不仅包括输入层的输出,还包括上一时刻隐藏层的输出.
长短期记忆网络LSTM 是循环神经网络的主流实现,是一类用于处理时间序列的神经网络,其神经元内部结构如图2 所示.在t 时刻,网络的输入有3个:当前时刻的输入值xt,上一时刻LSTM 的输出值ht-1,上一时刻的记忆单元ct-1;输出有2 个:当前时刻的输出值ht,当前时刻的记忆单元ct.

图2 长短期记忆网络神经元内部结构Fig.2 Internal structure of LSTM neuron
LSTM 的关键在于如何控制记忆单元c,为此,LSTM 设计了3 个开关,即门控单元:输入门、遗忘门和输出门.
1)输入与门控单元.
输入:

输入门:

遗忘门:

输出门:

其中,σ 为sigmoid 函数.
2)记忆状态单元的更新.

3)输出.

LSTM 用遗忘门决定上一时刻的记忆单元ct-1有多少保留到当前时刻ct,用输入门决定当前网络的输入xt有多少保留到当前时刻ct,用输出门控制当前记忆单元ct有多少输出到当前ht.
2.2 全过程沉降重计算Seq2Seq 模型
LSTM 常常用来构建Seq2Seq 模型,如图3 所示.在训练全过程沉降修正模型的过程中,输入是每个时刻的施工参数、土层参数,输出是每个时刻的沉降.对于encoder 部分,将训练数据按时序输入,得到encoder 部分的最终记忆单元值cn和最终输出hn,再用cn和hn来初始化decoder 最初的c0和h0.训练的输入包括1)施工参数:时间、加载和卸载等;2)土层参数:各土层的压缩模量E、厚度h 等.
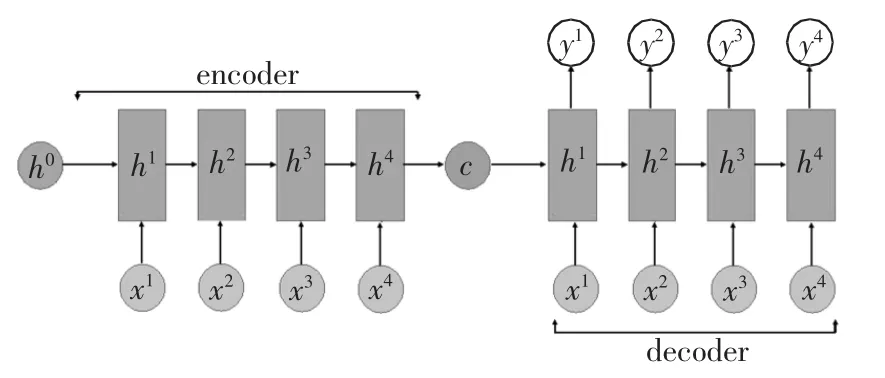
图3 全过程沉降数据重计算Seq2Seq 模型Fig.3 Seq2Seq model for recalculated whole process settlement data
对于decoder,再次将训练数据按时序输入,在每个时间点t,输入为xt,标签为yt.训练标签为各时段对应的实测沉降值.训练网络的目的是让LSTM每个时刻输出的ht与标签yt尽可能接近.通过建立ht与相应时刻yt的损失函数MAE,利用梯度下降法训练网络,使损失逐步降低以达到预期值.
3 Seq2Seq 模型的应用与验证
深度学习需要首先根据实际数据反演输入与输出的映射关系,脱离实际数据来讨论深度学习是无意义的,因此,直接将工程实测数据分析作为出发点是深度学习的必然要求.
3.1 工程背景
某大型机场填海面积26.0 km2,从某岛礁地基处理一期工程中2 000 余测点的实测沉降曲线中可以看到,由于观测、仪器等误差,测得的部分测点沉降曲线不符合沉降理论的预期,违背沉降发展规律,集中体现在出现大幅波动的锯齿状曲线这一现象.但从工程的实际情况来看,堆载测点并未卸载,应只有下沉,不可能出现回弹.这说明测得的锯齿状曲线与测点实际的沉降发展曲线相比有很大的偏差.除去观测误差的影响,现场实测曲线还存在某时间段数据缺失、测试员随意写入沉降数据等多种问题.由于机场建设非常关注全区域不均匀沉降带来的影响,而问题测点的数量较多,因此需要对这些异常测点数据进行预处理.
3.2 模型的验证与应用
Seq2Seq 模型训练与验证过程如图4 所示.首先需要人工对数据进行遴选,挑出符合经典沉降理论预期的优良测点数据作为训练集和测试集;然后定义网络超参数(非网络参数),对于上述Seq2Seq 模型,即选取神经元数量;之后网络参数的调整过程是模型根据反向传播自动进行的,无需人为干预;模型训练完成后,如在训练集和测试集上都收敛,则可应用到异常测点数据处理,否则需要重新调整神经网络超参数或重新选取训练集与测试集,并再次训练网络.
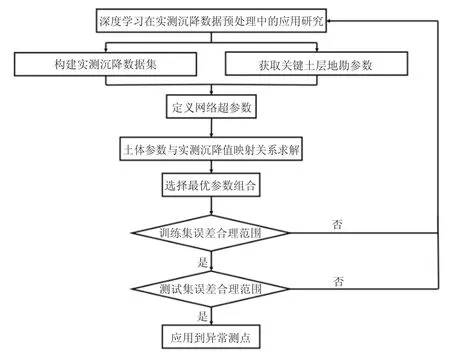
图4 模型训练与验证过程Fig.4 Training and verification process of model
模型训练完成后,在测试集所有测点上的全过程平均误差为32 mm.图5 为A 区部分测点的实测与重计算对比图,从图5(a)(b)(c)曲线的前半段可以看到,由于前期的沉降过程差异较大,在数据不够充足的情况下,模型很难精准修正,所以前半段的平均误差达到53 mm.到曲线后半段,模型能够发现沉降逐步偏向平稳的趋势,且精度提升明显,后半段平均误差为8 mm.图5(d)全过程平均误差为9 mm,低于全部测试集测点的平均误差值32 mm,且全过程都较为准确.图5 表明,深度学习模型对各种沉降发展模式,即各种形状的实测曲线,都能做到较为精确的重新计算,而传统方法很难处理突变等复杂状况.且深度学习模型计算后半段曲线的精确度明显高于前段,对于预测工后沉降来说,曲线后期的发展趋势显然更重要.
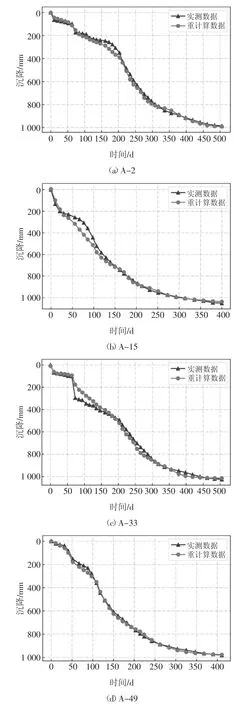
图5 A 区测试集部分测点实测与重计算沉降对比图Fig.5 Comparison figure of the measured and recalculated settlement of some points in the test set of area A
4 模型学习能力的影响因素
为探究模型学习能力的影响因素,也为证实前文所述深度学习的普适性,另选取该机场B 区与C区的测点训练并测试模型,得到的结果与A 区作为对比.
4.1 数据量
深度学习是数据驱动的科学,模型能否取得优异的表现,数据量的大小是决定因素之一.
如表1 所示,模型在B 区测试集上有91 mm 的平均误差.B 区误差偏大的原因是模型仅使用16 个测点作为训练集数据,来重计算测试集的8 个测点.B 区的数据较少,严重限制了模型的泛化能力.逐渐增大数据量后,模型的精确程度有了很大的提高,在C 区测试集上误差缩小到22 mm.从使用的数据量来看,B 区与C 区的结果均在合理范围内,这也反映了深度学习的普适性.

表1 不同区域模型的沉降误差Tab.1 Settlement error of different region
4.2 神经元数量
LSTM 神经元的个数对模型的学习能力有很大影响.神经元选取的数量需要逐步调试,数量过少会导致欠拟合,模型在训练集上都无法做到收敛;数量过多模型会出现过拟合现象,在测试集上的表现明显变差.
表2 展示了神经元数量选取16、32、64、128、256对模型计算沉降值与真实沉降值之间平均误差的影响.神经元数量越多在训练集上的表现越好,因为此时模型的学习能力变强.在测试集上则存在一个极值点,神经元数量偏少时,模型学习能力不强,无法通过训练集数据学习到沉降发展的规律;数量偏多时,模型由于强大的拟合能力,开始过度关注训练集数据,将其中的异常噪声也进行学习.模型在测试集上的表现是问题的核心,对于A 区测点数据选取64个神经元,此时模型在测试集上表现最优.
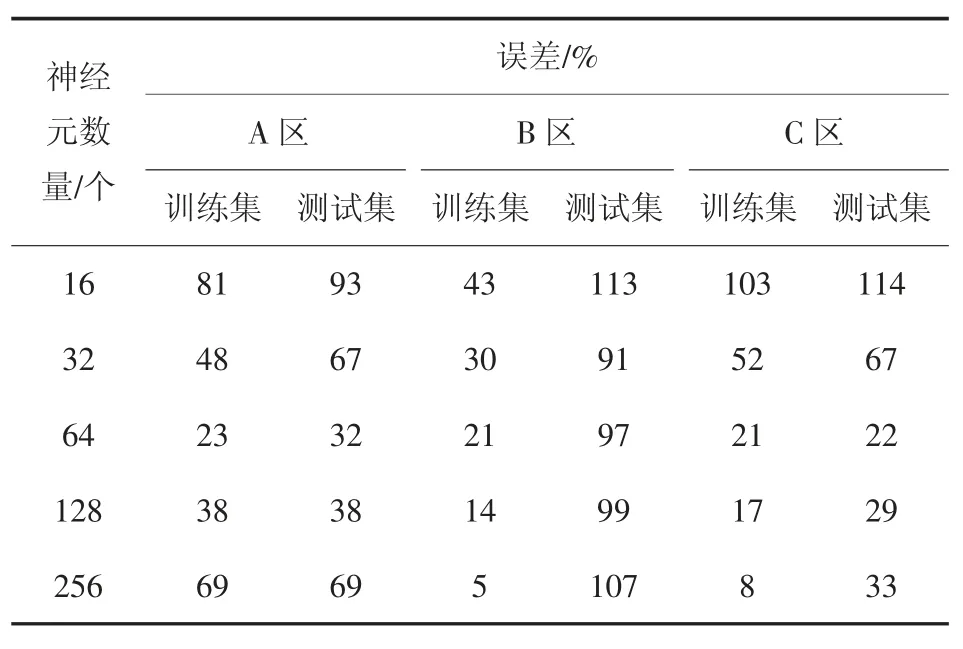
表2 神经元数量对误差的影响Tab.2 Effect of neuron numbers on settlement error
4.3 数据分布
图6 为B 区测试集8 个测点的实测与重计算沉降对比图.图6 中的主要误差都来源于测点B-52 和B-53,而其他测点的重计算情况相对较好,这说明除了数据量对模型误差的影响外,还存在其他重要影响因素.B 区训练集测点的淤泥层厚度、黏土层厚度见表3.图7 由表3 数据绘制而成.
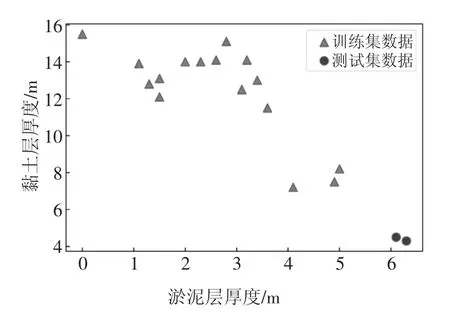
图7 训练集与测试集偏差分布图Fig.7 Deviation distribution of training and testing set
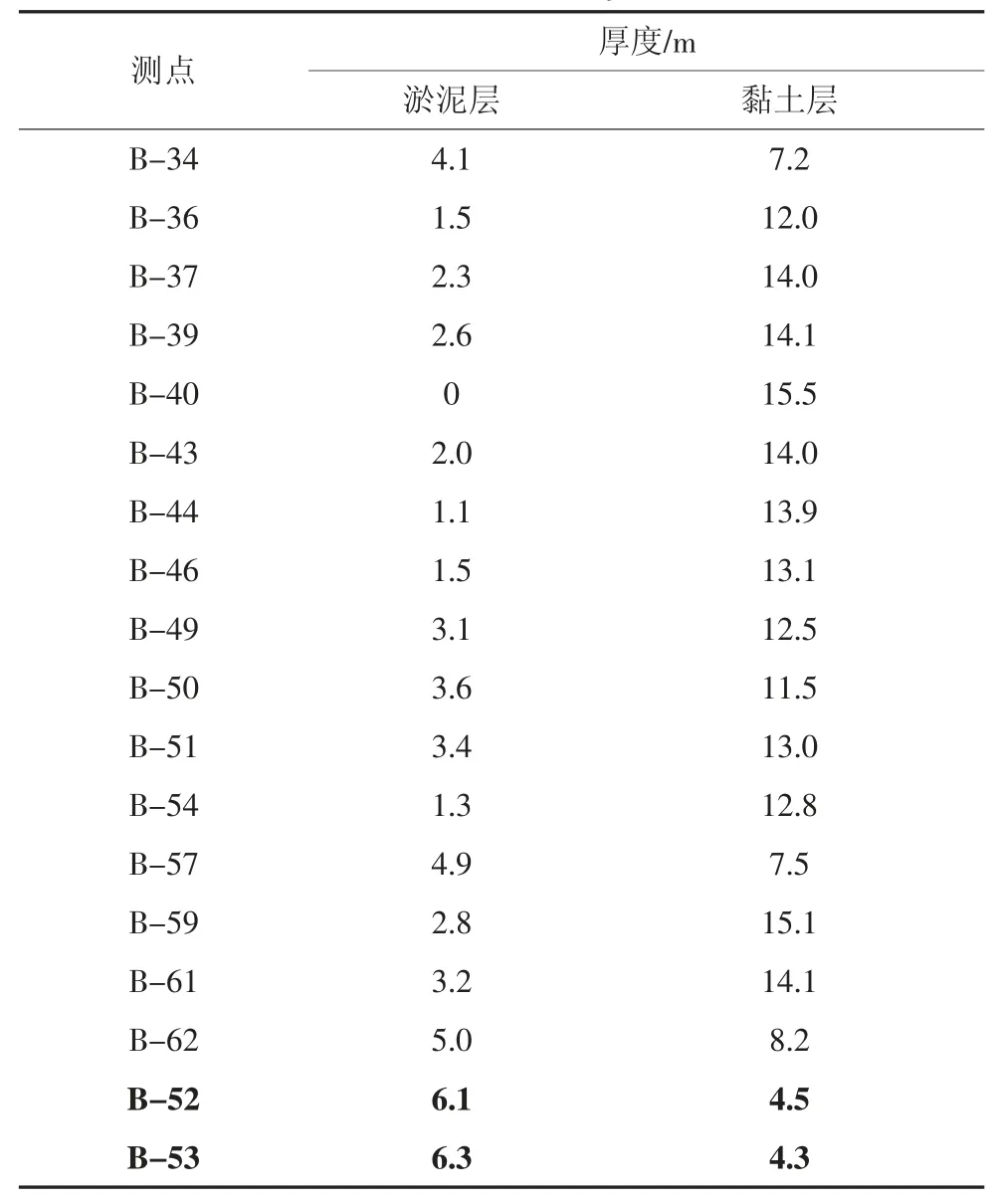
表3 测点土层参数表Tab.3 Parameter of soil layer in data set

图6 B 区测试集实测与重计算沉降对比图Fig.6 Comparison figure of the measured and recalculated settlements in the test set of area B
表3 最后两行黑体字部分为测试集误差主要来源B-52 和B-53 的参数值,其余为训练集测点的参数值.从图7 可以看到,训练集测点的黏土层厚度大多数在10 m 以上,而淤泥层的厚度在4 m 以下,与B-52、B-53 的土层厚度相差较大,由于训练集的数据分布与测试集差异很大,且数据量偏少,模型无法学习到淤泥层、黏土层厚度增大或减小造成的沉降具体增减量.模型主要训练在黏土层厚而淤泥层薄的数据集上,B-52 和B-53 的黏土层厚度过小,因此计算出的最终沉降会偏小.
在数据较少的条件下,数据的分布会造成模型预测结果不够精确.划分数据集时,应该尽量让训练集和测试集具有相同的数据分布.将B-52 或B-53中的任意一点加入训练集可以部分弥补训练集和测试集分布的偏差,尝试将B-52 加入训练集后,模型在其余条件不变的情况下测试集误差减小至57 mm,相较之前有明显提升.
4.4 数据特征
图8 为测试集测点C-16、C-22 的沉降曲线对比图,其土层参数见表4.

表4 C 区测点土层参数Tab.4 Soil parameters of area C

图8 C 区测试集实测与重计算沉降对比图Fig.8 Comparison figure of the measured and recalculated settlements in the test set of area C
C-16 与C-22 的土层参数相差不大,但C-16 在沉降发展到350 d 后误差明显变大.这说明施工条件仅考虑加载,土层参数仅考虑压缩量较大的淤泥和黏土限制了模型学习能力.C-16 显然是受到如渗透系数、排水条件等其他因素的影响.在数据偏多的情况下,应该考虑更多的影响因素,加入更多的数据特征.
在加入渗透系数作为数据特征后,C-16 的沉降对比曲线见图9(a),误差由之前的21 mm 降低至10 mm,且曲线后段提升效果明显.C-22 在考虑了渗透系数后,计算误差降低到2 mm.
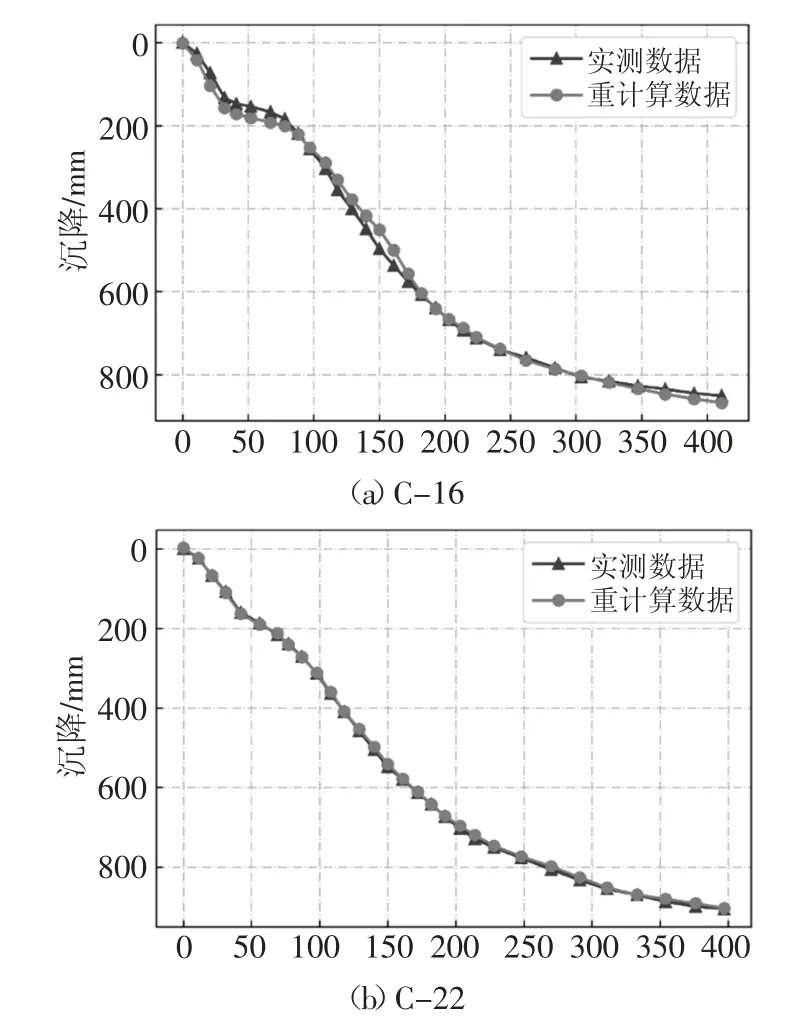
图9 考虑渗透系数后C-16 与C-22 沉降对比图Fig.9 Comparison figure of C-16 and C-22 considering permeability coefficient
5 结论
通过搭建Seq2Seq 模型,首次提出了深度学习在实测沉降数据预处理中的应用方法.在某机场不同典型区域A、B、C,通过对比模型在测试集上的重计算与实测沉降值,验证了深度学习对异常沉降数据进行预处理的可行性.其中,Seq2Seq 模型在A、C区域沉降数据的预处理中,将全过程平均误差分别控制在3 cm 和2 cm,表明此方法对工程实测沉降数据预处理及后续预测具有较好的实用价值.最后,还分析了超参数与数据集对模型学习能力的影响程度.具体结论如下:
1)数据量对模型处理异常数据的能力起决定作用,模型输出误差随数据量增大明显变低.样本数量作为统计方法的重要参数,是深度学习在岩土工程中的应用能否取得成功的基石.增大样本数量时,模型在B、C 区域测试集上的误差由91 mm 降低至22 mm.
2)训练集与测试集的参数一致性对模型性能有很大影响.在B 区的测试过程中,B-52、B-53 测点的淤泥层与黏土层厚度与训练集相差较大,导致模型测试与学习的内容不一致,造成B 区的重计算精度明显偏低.因此在划分数据集的过程中,应尽量保证训练集与测试集的数据特征分布大致相同.具体操作时,多次随机选取训练集,分别训练完成后对测试集结果取均值,一般能弱化这种差异.
3)所选数据特征的代表性对模型输出精度影响较大.若模型反复调试后,依旧达不到精度要求,应考虑所选输入是否具有代表性.此时可根据具体数据状况逐步增加数据特征,直至模型的重计算值达到精度要求.例如,相较于初次训练测试时仅考虑压缩模量与各土层厚度,增加渗透系数作为输入后,C区误差明显降低.
4)超参数的最优解会随具体数据集变化而不同,需根据具体的数据状况进行逐步调试,应避免过拟合与欠拟合现象发生.神经元数量、学习率、优化器、数据批次、网络层数等是模型自身超参数,其调节一般都是试错的过程.在算力充足的条件下,可对每个超参数设定一个数值或类型范围,对它们的组合全部进行训练.训练完成后,在测试集上进行验证并挑选合理结果.若时间有限,在固定其他超参数为默认值的条件下,可优先调节神经元数量与学习率,同样能够取得较为理想的结果.
——以徐州高层小区为例

