基于BP 神经网络CFRP 约束混凝土抗压强度预测

马高，刘康

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.工程结构损伤诊断湖南省重点实验室（湖南大学），湖南 长沙 410082）

纤维增强复合材料（Fiber Reinforced Polymer，FRP）以其优越的材料性能可对混凝土提供有效的横向约束，从而提高混凝土柱的承载能力和抗震性能.随着对FRP 约束混凝土力学性能研究的不断深入，国内外已经积累了大量的试验数据和混凝土本构模型[1-3].Singh 和Patra[4]收集了755 个试验数据对56个FRP 约束混凝土强度回归模型进行了评价，发现部分模型的预测结果偏于保守，按回归方法得到的抗压强度预测值远低于试验数据；而部分回归模型的预测值与试验值之比的平均值高达2.2～3.8，且预测结果变异系数较大.显然，按传统统计回归方法得到的强度预测模型具有一定的局限性.BP 神经网络由于其优异的自学习和自适应能力，具有良好的研究与应用前景.朱先勇等[5]通过BP 神经网络的训练和神经元间连接权值的调整，建立了合金成分与球墨铸铁组织和力学性能的复杂联系.唐和生等[6]建立了基于人工神经网络的矩形混凝土柱屈服性能的预测方法，发现与经验预测模型相比，神经网络方法吻合程度更高.在FRP 加固混凝土结构方面，也已开展了一些研究[7-9]，均发现BP 神经网络能对结果进行很好的预测，具有较强的映射能力.

目前神经网络的研究大多集中在提高预测精度方面，而对于如何把结果形成简单的数学表达式的研究还很少.Jφrgensen 等[10]利用BP 神经网络原理将压弯荷载作用下钢筋笼增强RC 柱承载力预测模型的权值和阈值输出成简单的数学表达式，相比于其他设计公式更加简单、且具有较高的预测精度.Leung 等[11]提出一种用图表和修正系数的方式来输出神经网络结果，该方法计算精度较好，但需要查图表，且修正系数公式较为复杂，不便于推广使用.Pham 和Hadi[12]用纯线性purelin 函数作为BP 神经网络的传递函数，相比用logsig 或者tansig 做传递函数的网络结构，该方法得到的预测精度有所下降，但是能够将神经网络结果输出为简明的线性方程.此外，由于原始数据可以互相组合形成新的数据输入，不同的输入形式对预测精度存在影响，Elsanadedy等[13]的研究表明原始数据输入形式和数据组合形式不同（如无量纲、几何物理形式等）对FRP 约束柱强度预测结果的影响较大.

因此，本文将神经网络方法引入FRP 加固混凝土柱抗压强度的研究中，在大量的试验数据基础上，建立各输入参数及组合形式与被约束柱抗压强度非线性映射关系的神经网络预测模型，最后根据神经网络输出结果提出理论计算公式和简化公式，为FRP 约束混凝土柱抗压强度模型的研究提供了新的思路.

1 FRP 约束混凝土强度模型

现有的FRP 约束混凝土抗压强度模型，大多数是基于Richart 等[14]针对主动约束混凝土提出的形式（公式（1）），其中k1为约束有效性系数，m 为回归曲线的形状参数.虽然k1、m 的取值通过回归分析得到，但其与FRP 约束混凝土的力学机理密切相关，较小的k1反应约束的有效性较差，m 则与fl/fco的增量对抗压强度的贡献大小相关，一般小于等于1.一些常见强度模型的k1、m 取值见表1.

表1 部分常见FRP 约束混凝土强度模型k1、m 取值Tab.1 Values of k1，m of the selected strength models of FRP-confined concrete

式中：fcc为FRP 约束混凝土抗压强度；fco为未约束混凝土抗压强度；fl为FRP 提供的横向约束应力；ffrp为FRP 环向抗拉强度；ρfrp为FRP 体积配置率；d 为混凝土柱直径；t、εfrp、Efrp分别为FRP 包裹层总厚度、FRP断裂应变、FRP 弹性模量.

除了上述公式中提到的参数外，FRP 种类、FRP强度测试方法同样会影响FRP 约束混凝柱抗压强度.比如：约束试件中FRP 实际断裂时达到的应力水平要低于FRP 条带拉伸试验测得的抗拉强度；生产商提供的材性指标一般高于FRP 条带拉伸试验结果.

2 神经网络的建立与训练

2.1 神经网络原理

BP 神经网络能够模仿人脑神经元对外部刺激信号的反应过程，基于多层感知器，结合信号正向传播和误差的反向调节，能有效建立用于处理非线性信息的智能化网络预测.BP 神经网络由输入层、隐含层、输出层组成，如图1 所示，通过改变网络的连接权值和阈值来适应外界环境，达到误差要求，输出最佳预测值.故BP 神经网络具有较强的容错能力、自学习能力和自适应能力.

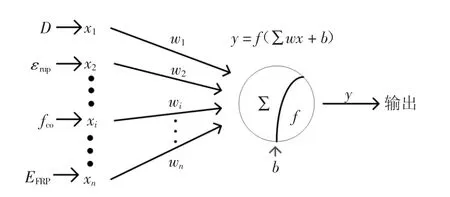
图1 神经网络拓朴结构Fig.1 Topolohical structure of BP neural network

2.2 试验数据处理与模型建立

由第1 节可知，在原始数据收集过程中应该对FRP 种类、FRP 抗拉强度测定方法进行分组，减少因数据来源不同而带来的误差.本文利用Sadeghian 和Fam[15]收集的251 组CFRP 约束混凝土圆柱的试验数据，其中CFRP 材性均通过条带拉伸试验获得.原始数据各参数的频率分布直方图见图2，可以发现：各试验数据变量相对集中，分布不均匀，试件直径主要分布于130～160 mm，原因为标准圆柱体试件（直径150 mm，高300 mm）使用最多；试验中未约束混凝土强度主要为常见强度范围（30～50 MPa）；FRP断裂应变、弹性模量主要分布于0.5%～1.5%、200～300 GPa.

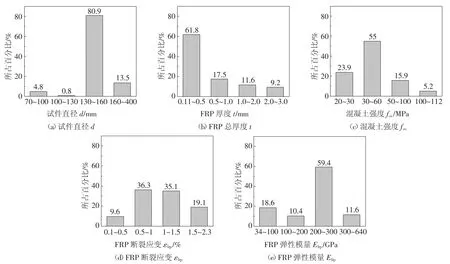
图2 原始数据各参数频率分布Fig.2 Frequency distribution of the parameters of raw data

由于所收集的数据往往不在同一个数量级，需将所收集的数据映射到[-1，1]之间，即归一化处理.本文采用的归一化公式为：

式中：xi是归一化后的输入值；x 是原始数据；xmax、xmin分别是这组数据的最大值、最小值，具体数值参见表2.

表2 输入输出参数统计表Tab.2 Statistics of the input and output parameters

本文按70%、15%、15%将实验数据随机划分为训练集、验证集和测试集.

由于原始数据可以互相组合形成新的数据，不同的组合形式会对FRP 约束混凝土强度的预测精度产生影响.为了得到最优的输入形式，本文考虑以下3 种神经网络模型：1）原始数据，即d、t、fco、εrup、Efrp，记为模型A；2）考虑物理意义，以ρfrp=4t/d、ffrp=Efrpfrup、fco为输入形式，记为模型B；3）无量纲形式，以γ=t/d、u=ffrp/fco为输入形式，记为模型C.即

模型A：

模型B：

模型C：

2.3 最优神经网络结构和模型选择

隐含层的神经元采用光滑、可微S 型对数函数sigmoid（见式（7）），将神经元的输入范围从（-∞，+∞）映射到（0，1）区间.本文的训练函数是trainlm函数，即用Levenberg-Marquard（LM）算法随机把输入向量和目标向量划分成训练、验证和测试集，该算法梯度下降快，训练步数少.

由于Hecht-Nielson 在理论上已经证明一个隐含层的BP 神经网络能够逼近任何区间内的连续函数，所以本文神经网络选用一个隐含层的结构，但隐含层的神经元个数需要试算确定.大量研究表明，增加隐含层神经元个数可以提高BP 神经网络的映射能力，但是神经元数目超过一定值后，网路性能反而降低.因此，一般采用R 值和均方误差MSE（Mean Squared Error）来确定隐含层神经元个数.图3 为A 模型在隐含层为7 个神经元时的训练集、验证集、测试集和总集经训练后的拟合情况，可见神经网络经过训练能很好地挖掘输入输出参数之间的关系，预测结果与试验结果的相关性趋近于1.为了得到最优神经网络结构，将不同神经元个数下的R 值和MSE 值绘于图4.可见在网络结构为5-8-1 时，MSE 值较小，预测精度高且稳定，因此模型A 的隐含层神经元数取8 个.

图3 A 模型5-8-1 网络结构下的R 值Fig.3 R values under 5-8-1 network structure of A model

图4 不同神经元个数下MSE 和R 值Fig.4 MSE and R values for different number of neurons

在最优的神经网络结构下，各模型的FRP 约束混凝土抗压强度预测值vpred与试验值vtest之比的统计信息见表3.从表中可以看出，A 模型的平均值为0.993，变异系数为0.083，计算精度高于B、C 模型，说明原始参数模型A 为最优模型，能够很好地挖掘输入参数与FRP 约束混凝土抗压强度之间的非线性映射关系.

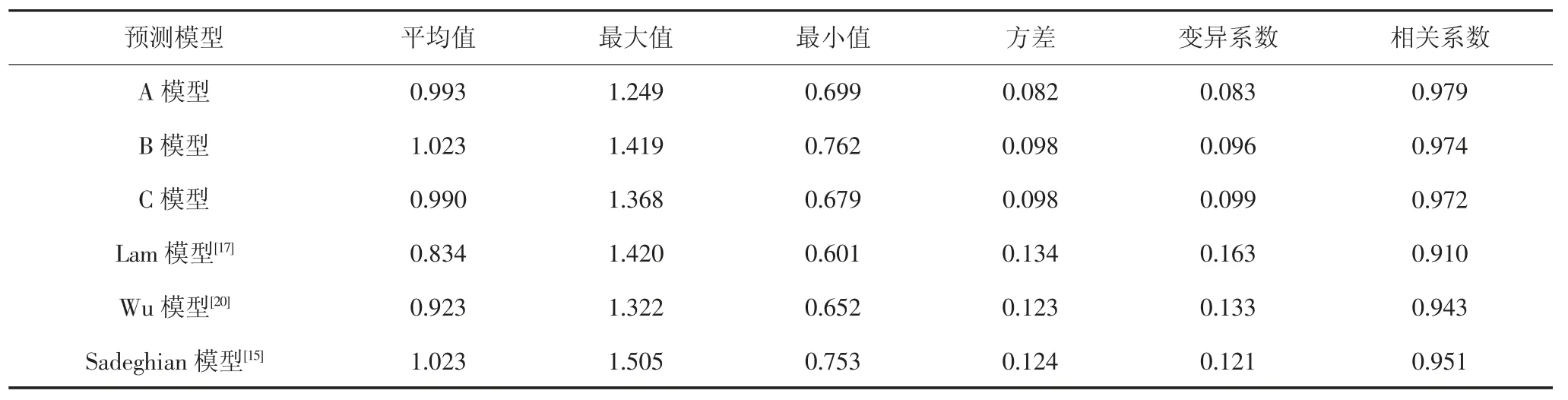
表3 FRP 约束混凝土抗压强度预测值与试验值统计比较Tab.3 Statistical comparison of predicted compressive strength of FRP-confined concrete with test results

2.4 与现有约束混凝土强度模型比较

考虑到文献模型提出时依赖的试验数据与本文所用的数据不同，本文选取3 个具有代表性的FRP约束混凝土强度模型进行比较，即Lam 模型[17]，Wu模型[20]和Sadeghian 模型[15]，其中：Lam 模型被ACI 规范采纳，在研究和工程应用中已被广泛采用；Wu 模型为基于大量试验数据的典型非线性模型；Sadeghian 模型来自本文引用的数据文献.BP 神经网络模型（模型A）、常用强度模型预测值和试验值对比情况见图5 和表3、表4.

通过表3 可以发现，神经网络模型相比常用强度模型预测精度更高、变异系数更小.从图5 和表4可以发现，各模型误差范围基本都在40%以内，Wu模型、Sadeghian 模型和Lam 模型的精度依次减小.神经网络模型中超过90%的数据点误差范围在15%以内，但回归模型误差在15%内的数据点个数不到70%，这说明神经网络模型相比于传统数据回归方法，能够更好地挖掘输入参数的数据信息.

图5 抗压强度预测值与试验值比较Fig.5 Comparison of predicted valueswith test results of compressive strength

表4 模型计算值与试验值比较Tab.4 Comparison of model predicted results with test results

3 神经网络结果公式化输出

神经网络通过不断调整权值和阈值，使网络误差最小或者达到期望要求，因此具有较高的预测精度.根据神经网络传播理论，可通过权值和阈值输出计算结果.为便于实际应用，本节将探讨用excel 输出网络结果和用简化的线性方程输出改进的神经网络结构.

3.1 理论公式推导

隐含层第i 个节点的输入neti为：

式中：iwij表示隐含层第i 个节点到输入层第j 个节点之间的权值；b1i表示隐含层第i 个节点的阈值.

隐含层第i 个节点输出ui为：

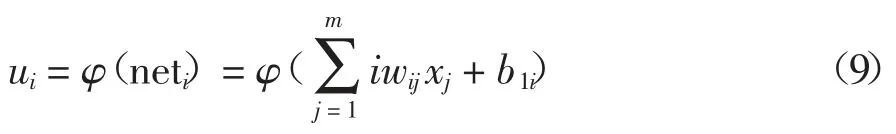
输出层第k 个节点输入netk为：

式中：lwki表示输出层第k 个节点到隐含层第i 个节点的权值；b2k表示输出层第k 个节点的阈值；φ 为隐含层激励函数，即传递函数sigmiod.

输出层第k 个节点输出为：

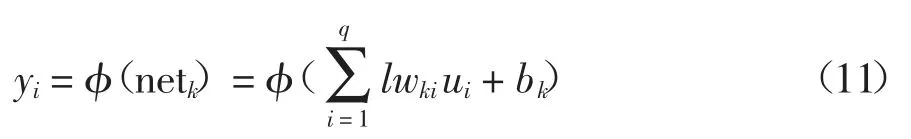
式中：φ 为输出层的激励函数，一般为purelin 函数：

3.2 一般公式结果输出

采用sigmoid 做传递函数的模型A 的最优网络结构的权重值和阈值见附录A，参照3.1 节，因此神经网络隐含层第i 个节点输入neti为：

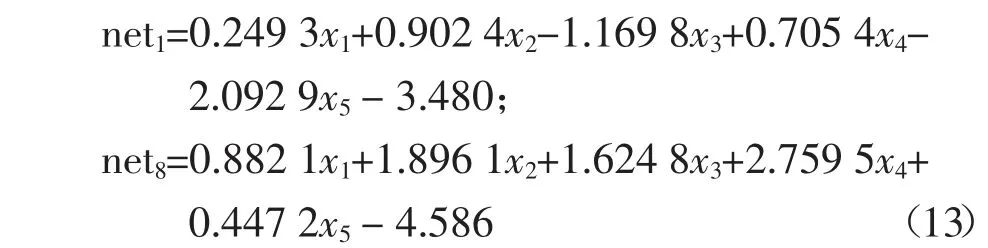
式中：x1，x2，…，x5分别对应d、t、fco、εrup、Efrp归一化后的值.

传递函数为sigmoid，因此隐含层节点输出ui为：

输出层的激励函数为purelin 函数，因此输出层输出为：

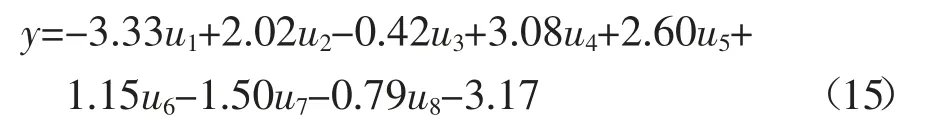
式中：y 是fcc归一化后的结果，可通过反归一化得到fcc，具体参考公式（3）和表2.基于以上公式推导，利用excel 计算表格得到的结果和模型A 预测结果完全一致，证明了该公式推导的正确性和神经网络结果输出的可行性.

3.3 简化公式

3.3.1 简化公式推导和模型选择

3.2 节中，模型A 采用sigmoid 函数作为输入层和隐含层间的传递函数时，网络结果需要借助excel等工具辅助输出，不便于推广应用.因此，本文采用purelin 函数代替sigmoid 函数做传递函数，期望得到具有较高精度而又形式简洁的线性方程式，其推导过程见图6（以m 个参数输入，隐含层为n 个神经元为例）.

图6 简化公式推导过程Fig.6 Derivation process of simplified formula

φ 函数采用purelin 函数时，式（10）可简化为：

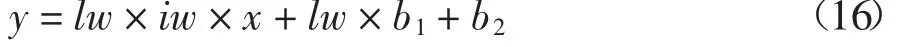
令：

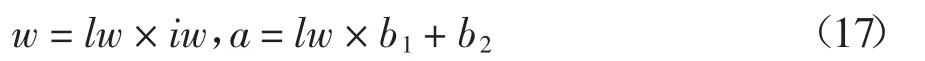
最终计算公式可以写为：

在推导简化公式时，考虑以下3 种数据组合形式：

1）模型1.fcc=f1（d，t，Efrp，εrup，fco）

2）模型2.fcc=f2（d，t，Efrp，εrup，fco，fl）

3）模型3.fcc=f3（fco，fl）

对比表3 和表5 可以发现，未进行数据组合形式下采用纯线性函数purelin 做传递函数的模型1比采用sigmoid 做传递函数的模型A 网络性能差，相关系数R 值仅为0.761，但将d、t、Efrp、输入参数组合成fl后（即模型3），神经网络预测精度明显提高，相关系数R 值增加到0.961，这说明：1）数据的不同组合形式对预测精度有影响；2）模型3 仅用纯线性函数purelin 做传递函数可以得到高精度的预测结果，说明FRP 约束混凝土抗压强度fcc与fco、fl近似成线性关系；3）模型2 和模型3 的区别为：在模型3 中，神经网络的训练和学习只能通过改变由d、t、Efrp、εrup组成的fl和fco的权值与阈值来适应，而在模型2 中，除fl、fco外，还可调整d、t、Efrp、εrup的权值和阈值，设置模型2 是为了得到更高精度的模型.但对比模型2和模型3 结果可以发现，模型2 添加d、t、Efrp、εrup后网络模型性能提升并不明显，且本文的模型3 已具备较好的计算精度，因此本文采用模型3 来推导简化公式.

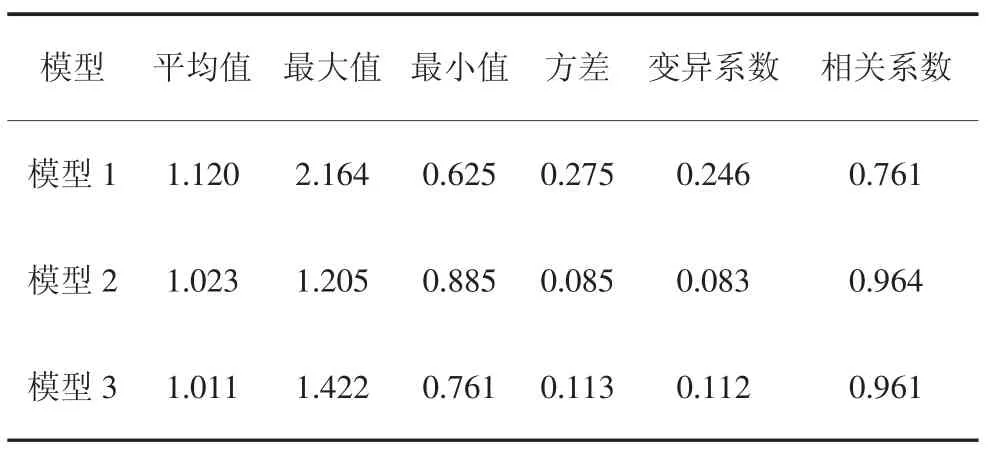
表5 模型预测值与试验值之比及统计参数Tab.5 Statistical parameters of predicted and test results

3.3.2 简化公式结果输出

采用purelin 函数的模型3 最优拓扑结构为2-7-1 形式，此时m=2，n=7，将其权重和阈值（附录B）代入式（17），得到

由于式（18）中x、y 是归一化以后的值，为了得到输入参数fl、fco和输出fcc的相互联系，将归一化式（3）代入（18），得到：

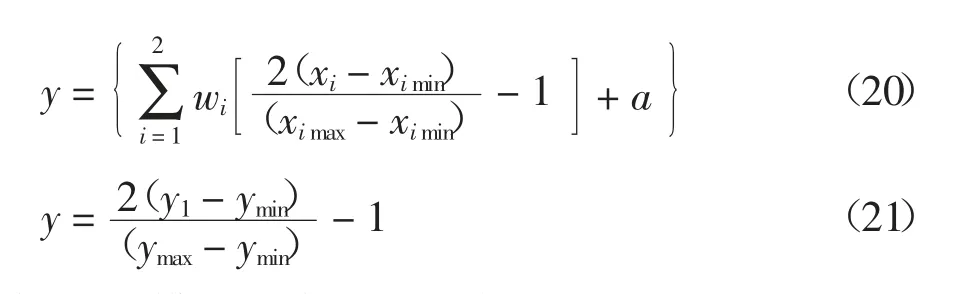
式中：xi为模型3 中归一化之前的fl和fco；y1、y 分别表示归一化前、后的fcc值；ximax、ximin分别为输入参数最大值和最小值，具体数值见表2.

联立式（20）（21），得：

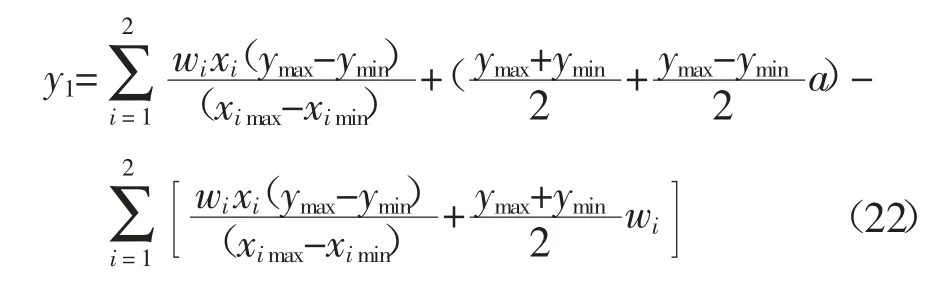
可将式（22）写成：

其中：

参考表2 及式（19）中的权重和阈值，代入式（24）（25）可得到：

ki中系数称为权重系数，代表各输入参数对输出参数的影响程度.

保留两位有效数字，得到：

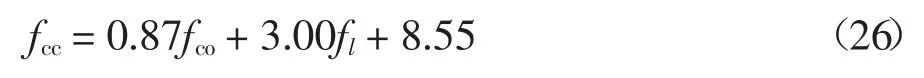
3.3.3 简化模型与非简化模型对比

图7 和表4 对比了各模型预测结果，可见采用purelin 做传递函数的简化模型3，相比采用sigmoid做传递函数的BP 模型，预测精度有所下降，但下降程度较小；用模型3 推导出的预测结果90%以上数据误差在20%以内，相比于回归模型预测精度更高，且变异系数更小.

因此，在使用BP 神经网络预测FRP 约束混凝土抗压强度时利用purelin 函数代替sigmoid 函数是可行的，模型3 推导出来的线性方程式（式（26））相比于传统回归模型，形式上仅增加一项常数项，但有更高的预测精度，且可以方便实际应用.

3.3.4 简化模型与数据回归模型对比分析

现有的FRP 约束混凝土强度模型大多是基于式（1）形式，其k1、m 取值依赖于所选择的试验数据.此外，参考式（26），考虑模型表达式为fcc=Afco+Bfl+C的情况.对2.2 节收集的251 组试验数据进行线性回归分析和非线性拟合分析，可得：

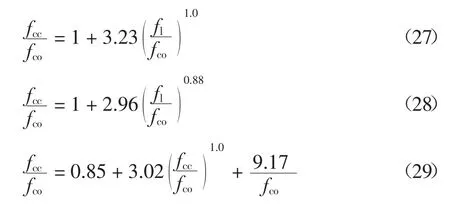
为精确评价模型的预测效果，引入IAE 指标（Integral Absolute Error）和MAPE（Mean Absolute Percentage Error）指标进行分析：

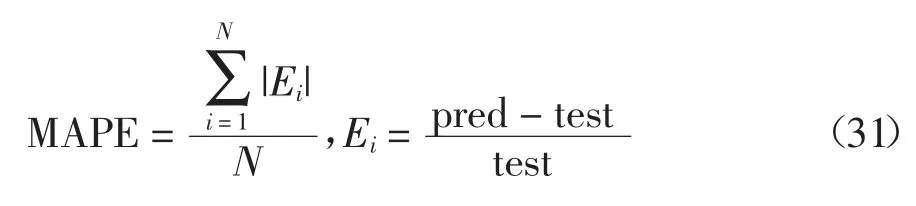
式中pred 和test 分别对应预测值与试验值.IAE 和MAPE 是对模型误差敏感的统计指标，IAE 和MAPE值越小，则模型误差越小.表6 为简化公式与本文回归模型预测结果的统计信息.可以发现，基于神经网络的简化模型的预测效果仅略低于采用表达式fcc=Afco+Bfl+C 直接拟合的结果，但要优于回归模型.

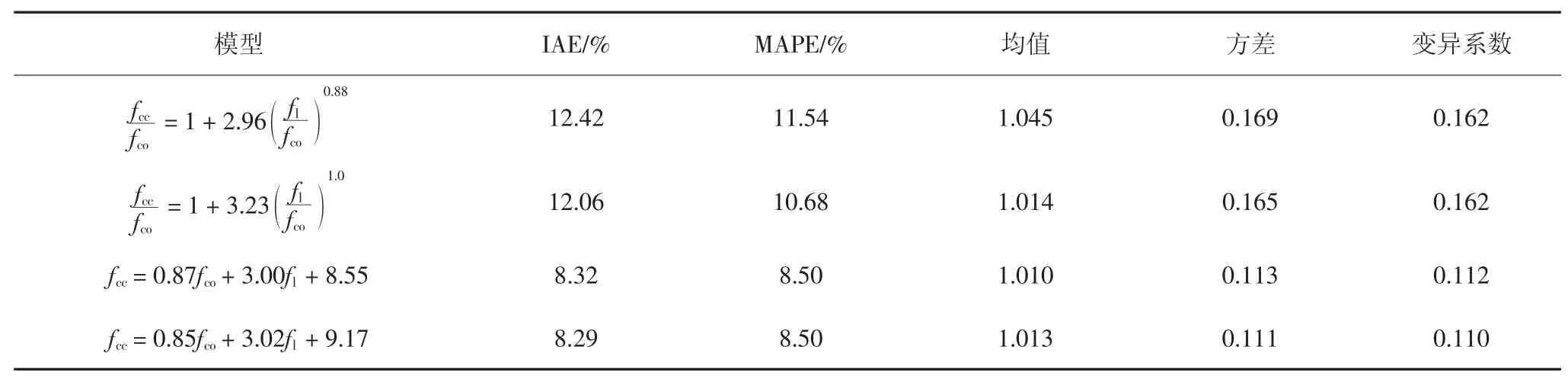
表6 简化模型与回归模型统计比较Tab.6 Statistical comparison of simplified model and regression model

对简化模型的公式变形如下：

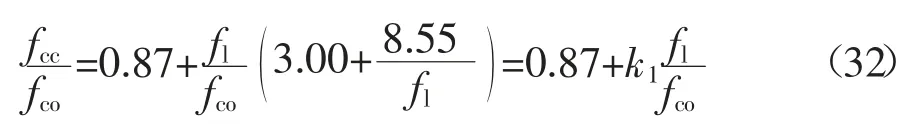
式（32）表明约束有效性系数k1是一个变量，随fl增大而降低，对于高侧向约束应力时，k1趋近于常数.值得注意的是，当fl为0 时，式（31）不能退化为素混凝土强度，由于实际应用时FRP 约束混凝土均会包裹一定厚度的CFRP（至少一层），因此其约束应力存在最小值.

已有不少文献在基于试验数据的回归分析时，也发现k1不是常数.Balmer[21]发现对于主动约束混凝土，系数k1在4.5 到7.0 之间变化，平均值约为5.6.Toutanji[22]通过FRP 约束混凝土试验结果的对比发现系数k1随fl/fco增大而减小，对于高侧向约束应力时，k1趋近于常数，主要原因是在高侧向约束应力下，混凝土的受压力学行为更接近弹塑性材料，其提出的约束模型公式如下：

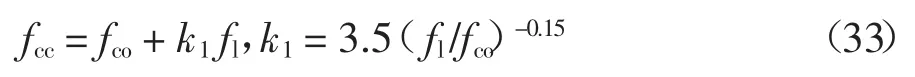
Fahmy 和Wu[23]也报道了相似的结论，且认为FRP 约束混凝土强度模型的k1值除了与fl相关，还与混凝土强度有关，其提出的约束模型如下：

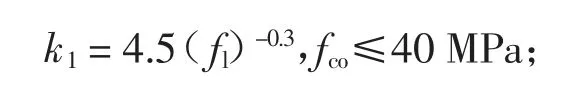
4 结论

现有的FRP 约束混凝土抗压强度模型大多是通过数据统计回归分析得到，但是由于FRP 约束混凝土柱的力学性能受多种因素影响，各回归模型预测结果相差较大，且有一定比例的数据预测值远大于实验值.本文在大量的实验数据基础上，用BP 神经网络对FRP 约束混凝土抗压强度进行预测与分析，发现：

1）BP 神经网络模型能够很好地预测FRP 约束混凝土抗压强度.神经网络模型中超过90%的数据点误差范围在15%以内，而回归模型误差在15%内的数据点个数不到70%.与回归模型相比，神经网络的预测结果精度更高、变异系数更小.

2）基于神经网络理论，将sigmoid 函数做传递函数的模型A 输出为数学表达式，并生成excel 工具表便于实际应用.利用纯线性purelin 函数代替sigmoid函数作传递函数的模型3 可生成形式简洁的计算公式，与模型A 相比，得到的简化公式计算精度有所下降，但下降程度较小，用模型3 推导出的预测结果90%以上数据误差在20%以内，其计算精度仍高于现有的回归模型.

3）仅用纯线性purelin 做传递函数的模型3，其预测结果的相关系数达到0.961，这说明FRP 约束混凝土抗压强度fcc与fco、fl近似成线性关系，且通过权重系数ki能看出横向约束应力fl对FRP 约束混凝土强度fcc的贡献远大于未约束混凝土抗压强度fco.

4）神经网络拟合结果是基于已有文献试验数据训练得到的，而非理论推导得到，因此其输出结果的物理意义尚不明确，只具有统计意义.从统计学角度看，神经网络结果优于常规的线性回归结果.

附录A

神经网络权值和阈值如下：iw 是隐含层到输出层的权重值，b1是对应的阈值，lw 是输出层到隐含层的权值，b2是对应的阈值.

附录B