双离合变速器车传动系统撞击声建模与仿真

张志军，唐 禹，杨宪武，田 雄，徐建春

（1.汽车噪声振动和安全技术国家重点实验室，重庆400000；2.长安汽车工程研究总院，重庆400000）

前言

双离合变速器（dual-clutch transmission，DCT）拥有两套离合系统，具备预挂挡功能，能够实现快速换挡。与自动变速器（automatic transmission，AT）相比，双离合变速器在某挡位运行中，有更多的空套齿轮副，在受到冲击转矩激励时，更易产生噪声问题［1］。Clunk是指汽车传动系统在受到突变转矩时，系统内部间隙部件间发生碰撞，而产生的一种金属撞击声［2］。在Clunk的研究方面，Kiran Govindswamy等研究了后驱自动变速器车型传动系统静态换挡Clunk问题，找出Clunk可接受水平，对换挡品质的提升给出指导意见［3］。Wan Joe Chen等基于台架试验研究了传动系统在模拟阶跃转矩下的瞬态响应，建立Adams模 型，得 出 与 试 验 相 近 的 结 果［4］。Daniel Wehrwein等建立了变速器涡轮转速与发动机转矩关系的元模型，得出发动机转矩管理最优解，来改善传动系统的Clunk问题［5］。Enrico Galvagno等建立双离合变速器车型AMEsim模型和变速器有限元模型，分析换挡过程同步器动作和壳体的振动，通过改变齿轮惯量来优化Clunk问题［6］。

本文中对比了Clunk降阶模型的不足，建立了全阶仿真模型，分析急踩油门（tip in）工况下系统的Clunk响应。通过对比分析发动机转矩控制、双质量飞轮刚度、阻尼、离合器输出转矩和驱动半轴刚度等软硬件参数对Clunk的影响，确定最佳的控制手段。

1 DCT传动系统建模

1.1 DCT传动系统构造

图1为该车型传动系统结构示意图。发动机曲轴末端连接双质量飞轮（dual-mass flywheel，DMF）初级惯量，双质量飞轮次级惯量连接离合器外壳，两个输入轴分别为奇数挡和偶数挡动力轴。动力通过中间轴、主减速器和半轴最终传递至车轮。

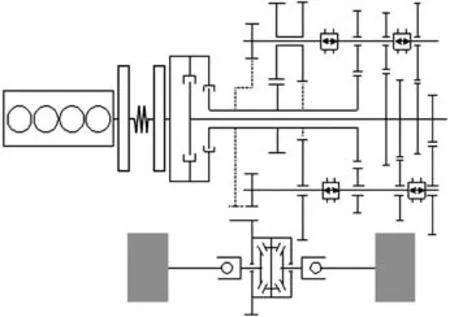
图1 整车传动系统结构简图

整个系统中存在的间隙为：挡位齿轮副（1～7挡、R挡）、第一主减齿轮副（FD1）、第二主减齿轮副（FD2）和差速齿轮侧隙，以及半轴球笼内接触间隙。系统内部间隙数量多，在突变转矩激励下，容易产生Clunk问题。

1.2 DCT传动系统模型

根据模型复杂程度，传动系统扭转模型可分为全阶模型和降阶模型。全阶模型包含传动系统可划分的所有集中质量参数，自由度数较多，模型较为复杂。降阶模型［7］是对全阶模型的简化，根据经验忽略部分零部件参数，或将其等效到相邻部件上，以降低模型自由度，减少计算量。对于Clunk的研究，多数采用降阶模型，即仅考虑动力传递链上的间隙和部件，其他非承载部件等效到相关联的承载部件上。但是降阶模型不能计算非承载齿轮的冲击，且可能造成等效部件计算的冲击值大于理论值的情况。

图2为三齿轮系统模型降阶为二齿轮系统模型的示例。在算例中，3个齿轮惯量J0、J1、J2相同，且节圆半径相同，在J0受到冲击转矩下，可分别计算出齿轮啮合力F1与F2。将模型降阶（J2惯量等效到J1）后，计算出新的啮合力F3。图3为2种模型的计算结果。可以看出，惯量等效后，主动齿轮J0受到的啮合力F3会高于原理论值F1，且降阶模型不能计算被等效齿轮J2的冲击力F2。

图2 三齿轮系统降阶示意图

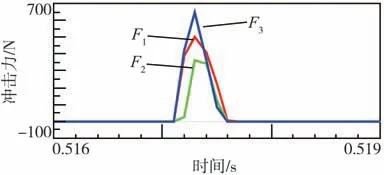
图3 三齿轮系统降阶前后冲击力计算值

针对以上情况，有必要建立传动系统Clunk全阶模型，计算所有间隙部件的实际冲击情况，找出贡献度较大的零部件。间隙部件之间采用间隙非线性刚度连接：在非接触区，刚度为0，在接触区，刚度为常数，如图4所示。对于非承载齿轮，拖曳力矩影响其冲击计算结果，不可忽略。空套齿轮的拖曳力矩包括轴承旋转阻力矩和齿轮搅油阻力矩，搅油阻力矩的计算参照文献［8］。传动系统全阶动力学模型示意图如图5所示。

图4 间隙刚度模型

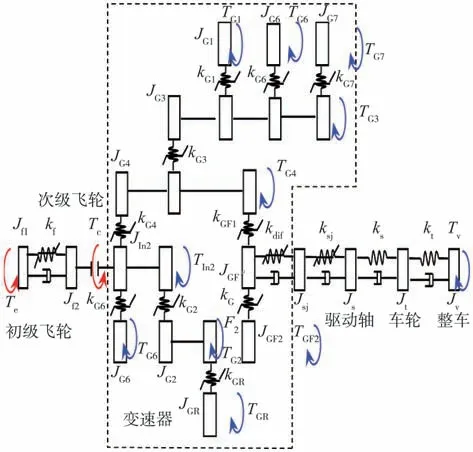
图5 传动系统全阶动力学模型示意图

整车Clunk模型共有17个自由度，其控制方程为

式中：J为惯量矩阵；C、K分别为阻尼矩阵和刚度矩阵，可以通过拉格朗日方程推导得出；θ为角位移向量，如式（2）所示；T为系统转矩向量，如式（3）所示。

式中：θf1、θf2、θIn2分别为双质量飞轮初级惯量、次级惯量、变速器输入轴的角位移；θGi为第i从动齿轮角位移；θs、θt、θv分别为驱动轴、车轮、整车等效惯量的角位移。

式中：Te、Tc分别为发动机、离合器转矩；TIn2、TGi、Tv分别为输入轴、第i从动齿轮、整车阻力矩。

考虑模型的复杂程度，采用AMESim求解。AMESim为多学科领域复杂系统建模仿真平台，软件内置汽车传动系统模型库，元件种类丰富，且计算耗时少、效率高。在以上17自由度传动系统模型基础上，搭配或替换AMESim简单悬架、轮胎、车身模块，构造更加详细的仿真模型，AMESim模型如图6所示。

图6 DCT传动系统AMESim模型

2 整车测试与模型精度校核

2.1 整车Clunk测试

为了分析Clunk产生规律，获取发动机、离合器转矩激励，校核仿真模型精度，开展了基于整车的Clunk测试。测试工况为Clunk问题工况：挡位保持在4挡，车辆加速至较高发动机转速后，松开油门使车辆滑行，待发动机转速落在1 600～2 000 r∕min范围内时，急踩油门，出现Clunk，重复多次以上测试过程，取冲击的平均水平。监测信息包括：车内主驾驶员右耳位置噪声、变速器近场噪声、变速器壳体振动、转向节振动，以及整车CAN信号中的动力系统转速、转矩等信息。为了观察Clunk瞬间动力系统输出转矩的变化，进行了驱动轴转矩测试。驱动轴转矩的测量采用PCB公司无线转矩测试设备8180，该设备通过应变片检测轴的扭转形变来获取转矩值，其供电和信号传输均为无线方式，质量小，对轴的动不平衡影响小。图7为车外测点分布示意图。转矩测试设备的安装如图8所示。

图7 车外测点分布示意图

图8 转矩测试设备安装

测试结果如图9所示，包含初级飞轮、输入轴转速、变速器壳体振动和驱动轴转矩。变速器输入轴转速在Tip in瞬间出现明显的波动，且后期没有和初级飞轮转速同步。从变速器Z向振动可以看到，整个Tip in过程总共出现3次冲击，分别对应输入轴转速波动曲线的第1个波峰点及其前后的2个波谷点，表明Clunk与输入轴转速突变存在直接关系。同时，在变速器输入轴转速上升阶段，半轴转矩也存在阶跃上升现象，由负转矩突变为正转矩。系统内部转矩的正负交替，将会使间隙部件从一侧接触转为另一侧接触，该过程出现冲击噪声。

2.2 模型精度校核

将试验条件下获取发动机转矩、离合器转矩时域值作为激励，代入传动系统AMESim模型进行计算，部分计算结果如图9所示，测试曲线与仿真曲线具有相同时间跨度。仿真相对试验的误差，从初级飞轮转速上升量、输入轴转速上升量、驱动轴转矩冲击值和驱动轴转矩最大值4方面来衡量（见图9中①～④），误差对比如图10所示。可以看出以上4个值的误差均小于15%。虽然仿真模型不能计算变速器壳体振动，但是非承载轮冲击力计算值同样出现3次峰值，且对应输入轴转速波动曲线的第1个波峰点及其前后的2个波谷点，该特征与壳体振动测试值特征相似。误差对比结果和冲击峰值时刻对比结果说明，仿真模型计算精度较高，可以用于后续的Clunk分析工作。

图9 测试仿真结果曲线对比

图10 测试仿真误差分析

3 Clunk仿真结果分析

3.1 激励-Clunk关系分析

前期仿真和试验得出，Clunk与变速器输入轴转速波动直接相关。为了直观了解输入轴转速波动的过程和原因，将整车传动系统简化为4自由度模型。此处仅是为了观测系统内部部件总体运动过程，而不是严格量化转速波动的幅值，因此对模型进行了简化。将变速器内部旋转部件视为一个部件，通过相对转角标记点判断初级飞轮、次级飞轮、输入轴的相对运动关系，简化后的观测模型如图11所示。

图11 系统主要部件运动关系简图

图12为模型部分计算结果，包含转矩、转速、双质量飞轮相对转角，共3组曲线。双质量飞轮相对转角曲线中，灰色背景区域为初级惯量-次级惯量空行程区间，扭转刚度为0。

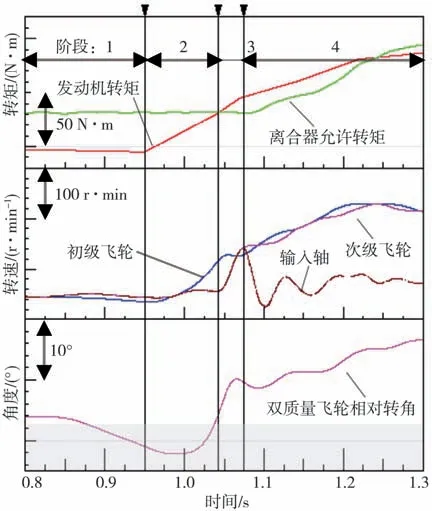
图12 系统主要部件运动关系简图

根据3组曲线变化特征，将Tip in整个过程划分为4个阶段。1阶段为Tip in前期的滑行阶段，发动机转矩小幅度缓慢降低，由驱动变为反拖，双质量飞轮相对转角由刚度区滑落至空行程区。2阶段为Tip in克服双质量飞轮扭转减振器空行程阶段，此阶段发动机转矩上升，但是减振器弹簧未压缩，减振器传递转矩不大，后方离合器未发生滑摩。3阶段为扭转减振器进入刚度区，由于弹簧压缩，次级飞轮转速迅速上升。变速器后方驱动轴开始承载一定驱动转矩，此阶段离合器依然未发生滑摩，变速器输入轴转速与次级飞轮基本一致。4阶段为离合器滑摩阶段，此阶段基础油压提供的离合器转矩不足以驱动负载，离合器进入滑摩状态，尽管离合器油压进一步增大，仍未能使离合器锁止。系统主要部件运动过程4个阶段示意，分别如图13所示。

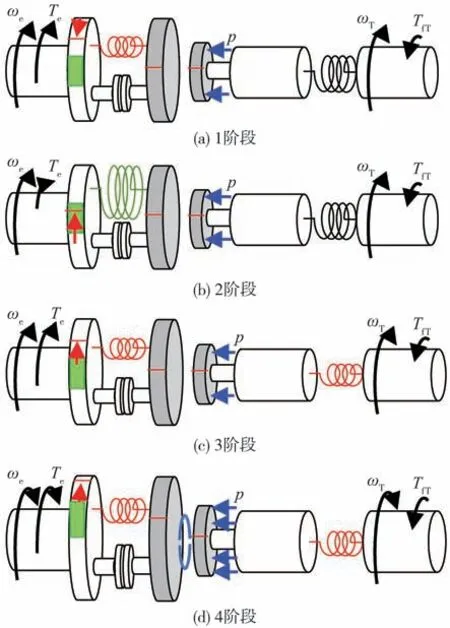
图13 系部件运动过程示意图

3.2 系统间隙部件冲击程度

为了分析系统内部冲击程度，差速齿轮冲击、驱动轴球笼内部冲击用绕驱动轴线方向的力矩表示，其他齿轮的冲击用啮合力表示。图14为非承载齿轮冲击力计算结果，图15为承载部件冲击力（矩）计算结果。可以看出变速器部分齿轮出现明显的冲击特征，而差速齿轮和球笼冲击特征不明显。为了方便对比空套齿轮与承载齿轮冲击力幅值的差异，对齿轮啮合力进行高通滤波处理，提取冲击力的峰值，如图16所示。从齿轮冲击力峰值看，明显的冲击现象不仅局限于发生在4挡齿轮、第1主减2对承载齿轮，还发生在3挡齿轮、第2主减等非承载齿轮。分析结果进一步证明进行全阶模型分析的必要性。

图14 非承载部件冲击力计算结果

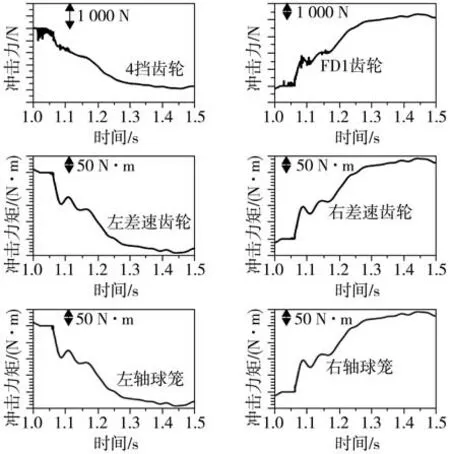
图15 承载部件冲击力（矩）计算结果

图16 齿轮啮合力峰值计算结果

4 Clunk敏感度分析与实车验证

4.1 Clunk敏感度分析

根据3.1节分析结果，变速器输入轴剧烈波动发生在Tip in过程的第3阶段。此阶段驱动力矩为发动机转矩，传递力矩的部件为双质量飞轮、离合器、驱动轴，因此选取发动机转矩、双质量飞轮扭转刚度与阻尼、离合器传递转矩、驱动轴刚度5个参数作为分析对象，分析其对系统冲击的影响。为了评价整个系统Clunk总体情况，引入总体Clunk指数概念（overall clunk index），计算公式如式（4）所示［9］。

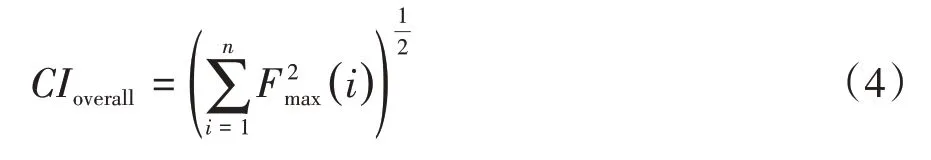
式中：CIoverall为总体Clunk指数；Fmax（i）为第i齿轮副在Tip in过程中产生啮合力高通滤波后的峰值。

由于总体Clunk情况主要取决于冲击排序靠前的齿轮副，因此采用二次方算法，更凸显主要贡献齿轮的效应。图17为总体Clunk指数对离合器传递转矩、双质量飞轮扭转刚度、阻尼、驱动轴刚度和发动机转矩斜率的敏感度分析结果。

图17 Clunk敏感度计算结果

可以看出，降低发动机转矩上升斜率能够有效降低总体Clunk，而离合器传递转矩、双质量飞轮刚度、阻尼和驱动轴刚度，在参数分析范围内，对总体Clunk影响较小。这也说明了在车辆传动系统瞬态冲击研究中，降低激励是控制冲击的重要手段。

4.2 实车验证

图18为发动机转矩上升斜率降低为斜率2前后的实车测试结果对比。降低发动机转矩上升斜率后，变速器壳体振动冲击峰值降幅约35%，降低比例与计算结果较为吻合。尽管降低发动机转矩上升斜率使动力响应变慢，但是经过综合评估，该变化程度不明显，且仅针对4挡发生Clunk的工况进行调整，对整车加速响应的总体影响不明显。

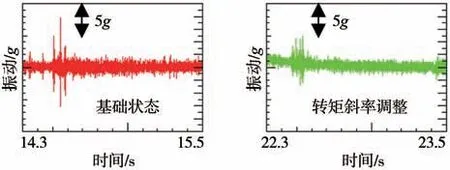
图18 转矩斜率调整前后壳体振动对比

5 结论

本文中建立双离合车型传动系统Clunk全阶仿真模型，通过对比实车测试结果，证明模型具有较高的精度。

完成Tip in过程传动系统部件运动情况分析，并计算间隙部件的冲击力，得出发生冲击较明显的部件，同时证明非承载齿轮也发生较为明显的冲击。

完成系统总体Clunk对发动机转矩、双质量飞轮刚度、阻尼、离合器传递转矩、驱动轴刚度的敏感度分析，计算结果和实车验证结果表明，降低发动机转矩上升斜率是控制Clunk的重要手段。