柳树风致响应的实测分析与预测

吴红华 徐海杰 李正农 钟旻 陈斌 李佳男 郝艳峰 赵帝 周立凡

摘   要：為探究在不同时距和不同风速条件下树干各个高度的风致加速度响应的分布规律，对单棵柳树的树前风场及其树干加速度响应进行了现场实测. 结果表明：树前顺风向脉动风速与风致树干加速度响应的概率分布特性有显著区别，树前顺风向脉动风速近似高斯分布，树干顺风向加速度响应的概率分布为明显的尖峰非高斯概率分布;柳树的风致响应为一个强迫振动的过程;采用广义Pareto极值算法计算其极值加速度响应，当时距为180 s时树前平均风速与树干顺风向极值加速度响应的相关性最高;对树前不同平均风速下树干不同高度的极值加速度响应进行拟合分析与预测，发现其树干顺风向极值加速度与树前平均风速呈二次非线性关系. 关于柳树的风致响应规律特性的探究，对于研究树木抗风具有重要的意义.

关键词：树木抗风;风致响应;加速度;极值;相关性

中图分类号：X43;P425.6                         文献标志码：A

Analysis and Prediction of Wind-induced Response of Willow

WU Honghua1，XU Haijie1，LI Zhengnong1，ZHONG Min2，CHEN Bin1，LI Jianan1，

HAO Yanfeng1，ZHAO Di1，ZHOU Lifan1

（1. Key Laboratory of Building Safety and Energy Efficiency of Ministry of Education（Hunan University），Changsha 410082，China;

2. School of Civil Engineering，Hebei University of Architecture，Zhangjiakou 075000，China）

Abstract：In order to investigate the distribution law of wind-induced acceleration response at various heights of the trunk，different time distances and different wind speeds，field measurements were made on the front wind field and trunk acceleration response of a single willow tree. The results show that there are significant differences between the probability distribution characteristics of wind-induced tree trunk acceleration response and wind-downwind pulsating wind speed. The wind-downwind pulsating wind speed approximates the Gaussian distribution，and the probability distribution of wind-downwind acceleration response of tree trunk is a sharp non-Gaussian probability distribution. The wind-induced response of willow is a process of forced vibration. The generalized Pareto extremum algorithm was used to calculate the extremum acceleration response. When the distance was 180 s，the correlation between the mean wind speed in front of the tree and the extremum acceleration response in the downwind direction was the highest. The response of extreme acceleration at different height of the trunk under different mean wind speed in the front of the tree was analyzed and predicted by fitting. It was found that the downwind extreme acceleration of the trunk had a quadratic nonlinear relationship with the mean wind speed in the front of the tree. The study of wind-induced response characteristics of willow is of great significance to the study of wind resistance of tress.

Key words：wind resistance of tree;wind-induced response;acceleration;extremum;correlation

随着我国经济的快速发展，市民的生活质量要求也提高了很多，许多城市已经将提高城市绿化覆盖率提上议程，行道树的种植与保护已经成为衡量一座城市环境质量的一个重要指标. 种植树木不但能够防风固沙，而且还能除尘降噪. 然而，我国又是一个台风频发的国家. 据统计，平均每年在我国东南沿海生成并造成影响的台风为8个左右，多的甚至达到14个[1]. 2018年9月，“山竹”台风肆虐广东，造成广州市内7 000余棵树木倒伏. 2019年9月，受“利奇馬”台风影响，温州市受灾树木达2万株，随处可见树木的折枝折干. 由此可见，强风不仅对于建筑物会造成影响，对树木所造成的伤害更为显著. 对强风作用下树木的风致响应进行研究显得尤为重要.

李国旗等[2] 研究了不同高度和不同风压下树木的应力分布. 他认为树冠形状是影响树木受损的主要因素，另外树木本身的特性和其所处的生态环境也将影响树木的抗风能力. 邵卓平等[3]设计了一套新的树木组合变形测量方法来预测树木所能承受的最大风力. 国外对于树木风致受力也进行了长期研究. Ken[4]测量了大风作用下树木的动力荷载响应. James等[5]研制了一种新型的测量大风期间树木动态风荷载的精密数字仪器，即通过两个正交传感器探头检测树干外部纤维的线应变. Ciftci[6]比对了一颗真实的树和模型树在相同风作用下的动态响应. 另外，建立合理的树木抗风模型是研究树木风倒破坏的重要基础. 国外学者（Ancelin[7]、Schindler[8]）等多是基于调查统计数据来分析破坏风荷载，缺乏理论依据. 国内学者有采用非线性力学静力求解的模型（宋晓鹤[9]），基于有限元振动频率的动力学模型（赖秋明[10]）来研究树木风毁机理，具有一定的片面性，难以反映真实的风致响应. 当前，学者们关于树木风致响应的测量研究仍处于初步阶段，对其规律特性并不了解，通过研究实际风致树木的极值加速度响应，结合计算风荷载以获得最真实的树木风致响应，将有助于更好地了解树木的风致破坏过程.

1   树木风致响应实测概况

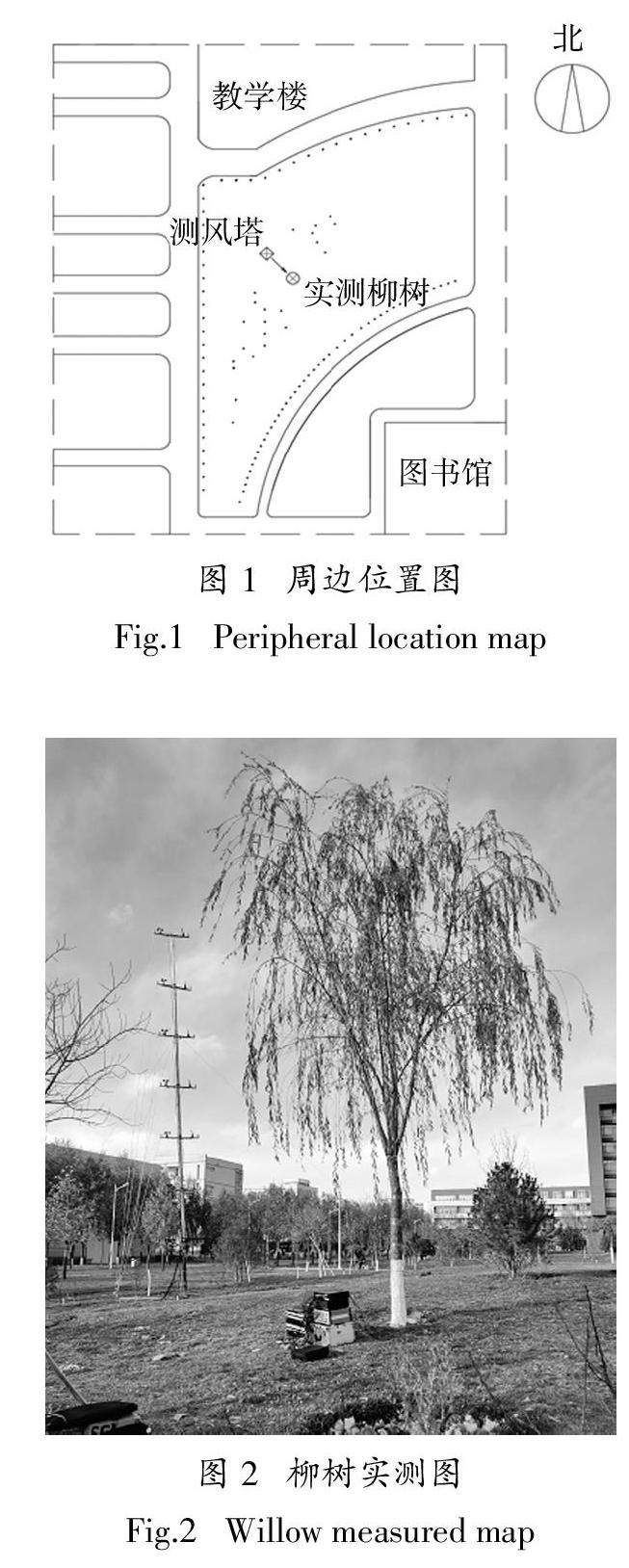
实测地点位于河北省西北部的张家口，该地区属于东亚大陆季风性气候，为我国少有的风能资源富集地. 该试验选取了河北建筑工程学院校区内图书馆与主教学楼间草地上的一棵柳树为试验对象. 柳树作为我国分布最为广泛的阔叶树种之一，大众的认知度很高. 乔木柳树在我国共有60余种，普遍在5～15 m的高度，枝条细长，叶片呈披针形或椭圆形，其树形优美，成长速度快，生态适应能力强，为许多地区广泛种植的一种观赏行道树的典型树种. 该实测柳树高8.4 m，主干高度2.7 m，胸径0.17 m（底径0.24 m，周径最小为0.14 m，树干笔直，尺寸基本相近），南北冠宽4.63 m，东西冠宽4.32 m，主干顶端为6条仅为主干一半大小的细长枝干，枝干尾部下垂，呈四散分布，具有柳树最主要的普遍特征，能够代表绝大多数柳树. 作为绿地景观树，常年受人工养护，场地四周空旷，无明显偏斜状态，树冠生长状况均匀且茂盛，较一般行道柳树更能体现柳树的动力风致响应.

试验时间为11月中旬，测试时主风向以西北风向为主，但实测风速风向具有一定随机性，需要同时测量其各点的风速风向. 图1～图3为该现场的周边位置图、柳树实测图及仪器测点布置示意图. 在测量树的西北方向架设测风塔，分别沿竖直高度方向1.5 m、3.0 m、4.5 m、6.0 m、7.5 m、9.0 m、10.5 m处布置采样频率为32 Hz的风速仪和风向仪. 加速度时程可以较为全面地反映树木树干部分的风致响应，故在柳树树干的西北向自下而上布置7个采样频率为256 Hz的加速度传感器，高度为0.4 m、0.8 m、1.2 m、1.6 m、2.0 m、2.4 m和2.7 m. 树干以上高度树枝柔软且枝重较轻，其振动易受到加速度传感器的干扰，所以不布置测点，仅对树干部分进行分析.

2   风致响应实测时程特性分析

2.1   数据处理

现场实测得280 min的树前风速时程和树干加速度时程分别如图4和图5所示. 通过两者时程图可以看出实测树前风速与树干加速度波动剧烈，树前风速幅值可以达到8 m/s（5级风）以上，树干加速度时程中也有大量超过0.1 m/s2的值，柳树风致响应效果明显. 相较于树前风速时程，树干加速度时程分布具有明显对称的分布特性.

为了使树前风速与树干加速度响应相对应，需要将实测的原始数据进行转化分解为树前顺风向脉动风速和树干顺风向加速度. 一般处理实测风速数据，常采用矢量分解法[11]将风速时程分解到正交的正南向（S）、正西向（W）坐标轴上（θ（t）为来流风角度与正南方向逆时针夹角），如图6所示.

计算时距T内两个正交轴的平均风速：

结合式（1）～（3），以测点7树前风速（10.5 m）为例分别对280 min的风速时程以不同时距计算平均风速 （图7）和平均风向角 （图8）. 通过分析图7和图8可以看出随着样本时距减小，平均风速和平均风向角波动范围变大，平均风速的波动程度大于平均风向角的波动程度. 不同时距下平均风向角稳定在315°上下变化，即该时段来流风以西北向顺风向风速为主，横风向风速大小可以忽略不计. 风速大小随时间变化剧烈，具有一定的非平稳性.

顺风向的脉动风速向量u（t）与横风向的脉动风速向量v（t）可按式（4）计算：

加速度放置角度为θa（t） = 315°，与平均风向基本一致，即为顺风向加速度. 取600 s时距为例计算结果如图9和图10所示. 后续以树前顺风向脉动风速和树干顺风向加速度为主计算.

2.2   树前风速与树干加速度响应的概率分析

绘制样本时程的概率密度分布图，分析其数据的波动规律，并与相应均值和方差的高斯分布进行对比. 为了进一步判别数据是否符合高斯分布，引入峰度和偏度的计算公式：

式中：N为样本数;μ为均值;σ为标准差. 式（5）和式（6）分别为峰度和偏度计算公式，即样本的4阶和3阶标准矩. 峰度又称峰态系数，反映概率密度分布曲线在平均值处峰值高低的特征数. 偏度是概率密度曲线相对于平均值不对称程度的特征数. 标准高斯分布的峰度为3，偏度为0，一般认为峰度大于3.5、偏度绝对值大于0.5的概率分布曲线为非高斯分布. 600 s时距树前顺风向脉动风速测点7（10.5 m）和相对应时间段的树干顺风向加速度测点7（2.7 m）的概率密度分布如图11和图12所示，其他时距概率密度分布与之相似.

计算不同时距的树前顺风向脉动风速和树干顺风向加速度的峰度、偏度和方差如表1和表2所示. 图11中树前顺风向脉动风速概率密度分布及其核密度分布与高斯分布十分贴合，且表1中不同时距各个高度测点的样本峰度小于3.5，偏度绝对值小于0.5，可认为树前顺风向脉动风速数据为高斯分布. 相对应的图12中树干顺风向加速度概率密度分布及其核密度分布与高斯分布相差甚远，通过表2可知其不同时距其峰度均远远大于3.5，随测点高度增加有减小的趋势;与峰度相比其偏度变化幅度并不大;方差量级较小，随高度增大. 所以该加速度分布具有很明显的对称性，属于典型的尖峰非高斯分布.

2.3   树前顺风向脉动风速与树干加速度响应的功率

谱分析

在振动问题中，我们将平均功率按频率分布的密度即单位频率范围内的密度定义为功率谱密度，绘制相应的功率谱有助于观察其不同频率能量分布情况，即其频域特性[12]. 根据傅里叶变换的性质，将与功率谱密度相关的自相关系数写成下列形式：

实际测量中，我们得到的数据一般为离散化的数据，对于傅里叶变换这种积分问题，常常将连续的积分离散化求和以进行计算，即快速傅里叶变换（FFT）.

通过随机样本序列的快速傅里叶变换来计算其功率谱密度，不可避免地会出现误差. 为了提高计算的准确性，将功率谱曲线光滑化，采用改进的平均周期图法估算样本序列的功率谱密度. 功率谱密度的单位是样本单位的平方与频率的比值，即风速功率谱单位为（m/s）2/Hz. 故为了方便对比，可将纵坐标功率谱无量纲化表示，即fs（f）→fs（f）/σ2，σ2为样本方差，横坐标频率不进行变换. 以600 s时距为例绘制其无量纲功率谱，如图13和图14所示，得到不同时距下各个测点功率谱能量峰值所对应的频率（表3和表4）.

分析图表，树前不同高度处顺风向脉动风速无量纲功率谱曲线能量分布相似，即测点7（10.5 m）高度以下能量分布受高度影响变化可以忽略不计，且不同时距功率极值频率均在0.1 Hz以下，来流风为大尺度漩涡，自振周期较长，尾部高频部分受周边环境影响毛刺较多.

相对应的树干顺风向加速度无量纲功率谱中，不同高度功率谱能量分布随高度增大而明显增大，但其曲线趋势相似，各波峰仍在相近频率，主峰值在0.55～0.65 Hz附近，为该柳树的主干频率.

对比该风速和加速度的功率谱，可以看出树前顺风向脉动风速的频率主要在0.1 Hz以下，而树干顺风向加速度的主干频率位于0.55～0.65 Hz之间，二者有明显的区别，即柳树的风致响应为一个强迫振动的过程.

3   柳树风致响应分析与预测

3.1   树前风场与树干加速度响应的相关性分析

通过前面的分析计算，树前顺风向脉动风速与树干顺风向加速度的变化趋势明显不同，树前顺风向脉动风速为高斯分布，而树干顺风向加速度趋向于尖峰非高斯分布. 本节引入极值算法计算风致响应的极值相关性，选取20～600 s间的最佳时距.

极值泛指稀少、重大等出现概率低的事件，关于如何求解极值本质上属于数理统计问题. 经过数百年的历程，关于极值理论的发展已经形成一套广泛的计算方法，但是具体应用于工程抗风实际，尤其是树木抗风领域仍是十分有限的. 一般关于极值模型的选取常采用经典模型和阈值模型. 经典模型即规范化样本的极值模型，只有区组样本极值作为观测数据，采用广义极值分布作为样本极值的概率分布模型. 对于小容量样本的经典极值理论算出的极值可能出现较大的误差，且其只利用了样本的单个极值信息，样本需求大，费时费力. 为了增加极值数据的利用率，提高拟合的准确性，学者们采用了基于超阈值数据的阈值模型. Pickand（1975）[13]选取了超阈值分布的样本，采用广义pareto分布（GPD）来推算极值分布. 李正农等（2015[14]，2017[15]）通过不同的参数选取方法得到相适合的阈值计算方法.

当有足够大的阈值u时，对于超出量y = x - u服从广义pareto（GPD）分布：

式中：μ、σ、ξ分别表示位置参数（阈值）、尺度参数和形状参数. 选择合适的阈值形成尾部样本数据，通过极大似然法计算其极值. 极值模型计算的关键在于阈值的选取，阈值选取的好坏直接关系到拟合的效果. 根据GPD分布，可以得出超阈值的平均超出量函数[14]：

由式（12）可以看出，当给定GPD分布的参数时，平均超出量函数为关于阈值的线性函数，由此可以通过观察e（u）的斜率变化，来观察该数据是否服从参数為σ、ξ的GPD分布. 根据式（12）以600 s和180 s时距的一个树干顺风向加速度样本为例，选取样本高尾部20%的数据计算其平均超出量，结果如图15和图16所示，其他时距与之相似.

尾部20%数据的平均超出量为关于阈值的线性函数，故可以采用广义pareto法拟合样本尾部分布. 通常学者们以10 m附近高度风速为基准风速，故本文根据式（13）分别对样本时距600 s、300 s、180 s、60 s、40 s和20 s，以测点7风速（10.5 m）为准采用广义pareto法计算树前平均风速与树干顺风向加速度的极值互相关系数ra，v：

在式（13）中ai，max为95%保证率下根据GPD法计算的树干顺风向极值加速度，i为不同时距树前样本平均风速. 选取等长度样本n = 28，不同时距下分别将整段数据计算求得的极值相关性系数求平均，可得结果如图17所示.

从图17中可以看出以180 s时距的树干顶端极值相关性最高，不同加速度测点高度和时距均对风致响应相关性产生影响，且高度越高相关性越显著，从60 s时距开始极值相关性受高度影响增大，位置越低处减弱得越快. 由2.3节分析可知，树前顺风向脉动风速频率在0.025 ～ 0.065 Hz之间，周期为15～40 s，树干主频率在0.55 ～ 0.65 Hz之间，周期为1.5 ～ 1.8 s，故时距在20 ～ 600 s之间的树木风致响应必然有一定相关性，结合图17所示，显然在180 s时距下树前各个高度的平均风速与柳树树干的加速度风致响应相关性最高，即180 s为计算风致响应的最佳时距.

3.2   树干的风致极值加速度响应预测

以测点7（v）所测的树前顺风向脉动风速为准，探究180 s时距下基于95%保证率GPD法的树干顺风向极值加速度响应与树前平均风速和高度的关系，如图18所示.

图18为树干各测点顺风向极值加速度与树前平均风速的分布图，式（14）～（21）为各拟合曲线公式及拟合优度，由上往下分别与图18中2.7 m、2.4 m、2.0 m、1.6 m、1.2 m、0.8 m和0.4 m的拟合曲线相对应. 式（21）为拟合优度，表示回归曲线对离散值的拟合程度，R2越接近1表示回归曲线越贴近原数据. 可以看出各个高度处拟合曲线R2均大于0.7，拟合程度极佳，即图18所示直线具有高度拟合性，其树前各个高度处平均风速与树干顺风向加速度均呈非线性正相关性，且一次项与二次项系数均随高度增加而逐渐增大. 树干顶部2.7 m顺风向极值加速度值曲率最大，进一步分析其拟合残差值如图19和图20所示，观察其残差值（y-yi）分布，绝对值不超过0.04 m/s2，绝大部分残差偏离程度较小，在 0.02 m/s2以内，均在可接受范围内.

柳树在大风作用下的加速度响应受风速增大而不断增大，但是实际上由于树木本身的材料特性限制，在达到某一特定风速时，必然会再发生弯曲、剪切或弯剪破坏. 树木的风致响应可视为由脉动风所引起的动力响应和由平均风所引起的静力响应两部分组成. 其中，柳树在动力响应下所受的最大力即为最大惯性力，可通过预测得到的极值加速度，再结合柳树的固有质量而得到;而柳树的静力响应，可通过树前风速、树木阻力系数、迎风面积等参数，计算静力风荷载而得到. 基于完整的风致响应，可以进一步判定柳树的破坏状态及破坏风速，这将在后续的研究分析中进一步展开.

根据式（14）～（20），对树干不同高度各测点顺风向极值加速度进行预测，则当树前顺风向脉动极值风速在14 m/s以上时，树干顶端极值加速度（表5）将超过1 m/s2，相当于7度地震烈度时的加速度.

4   结   论

通过对柳树的风致响应进行实测分析，探究柳树风致响应的时程特性、功率谱、概率密度等性质，且应用极值计算理论，研究树木在强风作用下的风致响应规律并对其进行预测，可得如下结论：

1）在自然条件下，柳树的树前风速和树干加速度时程幅值波动较大，变化趋势并不一致，树干加速度响应具有明显的对称性. 树前顺风向脉动风速更接近高斯分布，而树干加速度响应峰度值远大于3.5，偏度小于0.5，主体部分偏向于尖峰非高斯概率密度分布.

2）作为行道树的典型树种，通过分析其功率谱，可以发现柳树的风致响应是一个强迫振动的过程，树干的主要振动频率明显高于树前顺风向脉动风速的主要频率.

3）由不同时距的相关性分析可得180 s时距为计算风致响应的最佳时距. 随着加速度测点高度减小，其相关性减弱.

4）最后对柳树不同高度的树干极值加速度风致响应进行拟合分析，两者呈现二次非线性关系，树干顶部的极值加速度最大.

参考文献

[1]    周利芬，吴红华，李正农. 树木抗风及对风环境影响的研究综述[J]. 自然灾害学报，2015，24（5）：199—206.

ZHOU L F，WU H H，LI Z N. Review of research on trees wind resistance and effects on wind environment[J]. Journal of Natural Disasters，2015，24（5）：199—206. （In Chinese）

[2]    李国旗，安树青，张纪林，等. 海岸带防护林4种树木的风压应力分析[J]. 南京林业大学学报，1999，23（4）：77—81.

LI G Q，AN S Q，ZHANG J L，et al. The bending stress analysis of 4 species of woods caused by wind pressure in coastal shelter forest[J]. Journal of Nanjing Forestry University，1999，23（4）：77—81. （In Chinese）

[3]    邵卓平，吳贻军，黄天来，等. 风灾害下树木强度分析的理论、方法及应用[J]. 林业科学，2017，53（5）：170—178.

SHAO Z P，WU Y J，HUANG T L，et al. Theory and method of tree stem strength analysis under wind disaster and its application[J]. Scientia Silvae Sinicae，2017，53（5）：170—178. （In Chinese）

[4]    KEN J. Dynamic loading of trees[J]. Journal of Arboriculture，2003，29（3）：165—171.

[5]    JAMES K R，KANE B. Precision digital instruments to measure dynamic wind loads on trees during storms[J]. Agricultural and Forest Meteorology，2008，148（6/7）：1055—1061.

[6]    CIFTCI C. Risk quantification of maple trees subjected to wind loading[D]. Massachusetts：University of Massachusetts Amherst，2012：54—78.

[7]    ANCELIN P，COURBAUD B，FOURCAUD T. Development of an individual tree-based mechanical model to predict wind damage within forest stands[J]. Forest Ecology and Management，2004，203（1/2/3）：101—121.

[8]    SCHINDLER D，BAUHUS J，MAYER H. Wind effects on trees[J].European Journal of Forest Research，2012，131（1）：159—163.

[9]    宋晓鹤. 云杉风倒静力学模型的建立及其分析[D]. 哈尔滨：哈尔滨工业大学，2006：23—42.

SONG X H. Building and analysis of mechanics model for windthrow of spruce[D]. Harbin：Harbin Institute of Technology，2006：23—42.（In Chinese）

[10]  赖秋明. 云杉风倒动力学问题的研究[D]. 哈尔滨：哈尔滨工业大学，2008：8—17.

LAI Q M. Dynamics research for windthrow of spruce[D]. Harbin：Harbin Institute of Technology，2008：8—17. （In Chinese）

[11]  吴本刚，吴玖荣，傅继阳. 高层建筑实测风场环境的非平穩性分析研究[J]. 空气动力学学报，2014，32（3）：410—415.

WU B G，WU J R，FU J Y. Non-stationary analysis on field measured wind speed data of tall buildings[J]. Acta Aerodynamica Sinica，2014，32（3）：410—415. （In Chinese）

[12]  方智远，汪之松，李正良. 雷暴冲击风作用下高层建筑风荷载频域特性[J]. 湖南大学学报（自然科学版），2020，47（1）：100—107.

FANG Z Y，WANG Z S，LI Z L. Frequency domain characteristics of wind loads on high-rise buildings under thunderstorm downburst[J]. Journal of Hunan University （Natural Sciences），2020，47（1）：100—107. （In Chinese）

[13]  PICKAND S J. Statistical inference using extreme order statistics[J]. Annals of Statistics，1975，3：119—131.

[14]  李正农，伍欢庆. 风压极值的阈值模型研究[J]. 地震工程与工程振动，2015，35（1）：189—198.

LI Z N，WU H Q. A study on extreme windpressure：POT model[J]. Earthquake Engineering and Engineering Dynamics，2015，35（1）：189—198. （In Chinese）

[15]  李正农，曹守坤，王澈泉. 基于Pareto分布的风压极值计算方法[J]. 空气动力学学报，2017，35（6）：812—816.

LI Z N，CAO S K，WANG C Q. Method of estimating extreme wind pressure based on the Pareto distribution[J]. Acta Aerodynamica Sinica，2017，35（6）：812—816. （In Chinese）