竖向荷载下软土中碎石单桩破坏模式及承载力计算

谭鑫 冯龙健 胡政博 赵明华

摘   要：采用有限差分法对软土地基中碎石桩单桩竖向受荷破坏全过程进行数值模拟研究. 引入考虑体积应变截断的塑性硬化模型模拟碎石桩体，能够较好地反映碎石桩体的非线性剪胀力学行为以及由此引起的桩土相互作用. 重点分析了桩体鼓胀变形、桩侧土压力演化以及由此决定的单桩破坏模式与典型荷载沉降曲线. 传统单桩极限承载力公式所假设的整体剪切破坏模式仅适用于刚度较大的土体，而在软土中局部剪切破坏模式更为常见. 为此，基于弹塑性介质中圆孔扩张理论推导了考虑桩体鼓胀变形及桩周土体刚度的碎石桩单桩承载力计算公式，并通过对比数值解验证了推导公式的有效性. 较为系统地研究了软土地基中碎石桩单桩的承载机理及破坏模式，可为进一步研究碎石桩复合地基承载机理打下坚实的基础.

关键词：碎石桩;破坏模式;极限承载力;圆孔扩张;数值模拟

中图分类号：TU473.1                             文献标志码：A

Failure Mode and Calculation Method of Ultimate Bearing Capacity

of a Single Stone Column in Soft Soil under Vertical Loading

TAN Xin1，2，FENG Longjian1，HU Zhengbo1，ZHAO Minghua1，2

（1. Institute of Geotechnical Engineering，Hunan University，Changsha 410082，China;

2. Key Laboratory of Building Safety and Energy Efficiency of Ministry

of Education（Hunan University），Changsha 410082，China）

Abstract：The finite difference method is used to numerically simulate the complete bearing and failure process of a single stone column under vertical loading in soft soil. The plastic hardening constitutive model considering volumetric strain interception is used to simulate the stone column，which can well reflect the nonlinear dilatancy mechanical behavior of the stone column and the resulting column-soil interaction. The bulging deformation of the stone column，the evolution of soil stress acting on the stone column，the failure modes and the corresponding typical p-s curves are analyzed. The overall shear failure mode assumed by the traditional formula is only applicable to soils with high stiffness，while the local shear failure mode is more common in soft soils. Therefore，based on the theory of circular hole expansion in elastoplastic media，the calculation formula of ultimate bearing capacity of single stone column considering the column bulging deformation and the soil stiffness is derived. The formula is verified by the numerical simulation solution. The bearing mechanism and failure mode of the single stone column in soft soil are systematically studied，which provides a theoretical foundation for further study on the bearing mechanism of composite ground reinforced with stone columns.

Key words：stone column;failure mode;ultimate bearing capacity;circular hole expansion;numerical simulation

碎石樁复合地基能够有效提高地基承载力、增强稳定性、控制沉降，并且施工简便、快速，工程造价较低. 碎石桩加固软弱地基的机理随被加固土质不同而有所差别，对松散无黏性土主要为挤密作用，而对于黏性土则以置换作用为主. 对于起置换作用的软黏土中碎石桩单桩承载破坏机制，国内外许多研究者都进行过较为深入的研究[1-5].

通常碎石桩入土深度大于临界长度时，就不大可能产生整体刺入破坏，一般不考虑整体刺入的失稳. 大量现场及室内试验[4-6]揭示当碎石桩埋置深度超过大约4倍桩径时，碎石桩的破坏是由桩体径向鼓胀变形引起的. Hughes和Withers[4]认为桩长超过一定深度时，碎石桩径向位移可以忽略不计. 一般认为碎石桩单桩在竖向荷载作用下，桩周土体提供的极限侧向土压力，可以按照三轴压缩状态计算碎石桩单桩极限承载力，即为桩周土体的侧向约束应力乘以散体材料内摩擦角相关的被动土压力系数. 大多数散体材料桩单桩承载力计算公式区别在于侧向约束应力的计算不同，最常用的是基于桩周土体沿直线滑裂面发生整体剪切破坏的Brauns公式[5].

Hughes和Withers[4]、Wong[6]和郑刚等[7]均采用类似破坏模式，以及赵明华[3]、贾尚华[8]等采用圆孔扩张理论推导了碎石桩单桩承载力公式. 但实际上桩周土体侧向约束力达到其极限值的过程是随桩体鼓胀不断增大的动态过程. 在桩周土体刚度较低的情况下，有可能在土体破坏失效之前桩体即由于鼓胀破坏而丧失承载能力. 因此，目前各类计算方法或未考虑土体刚度的影响，或未考虑碎石桩自身鼓胀破坏的影响，极有可能高估了软土中碎石桩单桩极限承载力. 由于桩土之间复杂相互作用限制了解析方法的应用，部分学者也通过数值模拟方法研究碎石桩的承载力问题[7，9-12]. 陈建峰等[12]通过数值模拟方法研究了碎石桩夯扩和载荷试验分级加载过程以及其在堆载和孔压消散过程中的荷载传递和变形特性. 谭鑫和赵明华等[9-11]分别基于连续和离散数值方法模拟碎石桩单桩荷载的模型试验，数值结果与试验结果较一致.

本文采用有限差分數值方法模拟软土中碎石桩单桩荷载试验，通过分析碎石桩在承载全过程中的沉降、变形及破坏过程，揭示碎石桩与桩周土体的相互作用机理与破坏模式，并根据破坏模式基于圆孔扩张理论推导能够考虑土体刚度以及桩体鼓胀变形影响的碎石桩单桩承载力计算公式.

1   碎石单桩竖向受荷的数值模拟

1.1   碎石桩体本构模型（塑性硬化模型）

碎石材料具有典型离散颗粒材料的一系列力学特性，最典型的是与密实状态、围压相关的摩擦强度及非线性剪胀行为. 由于软土地基中碎石桩所受的侧向土压力相对不大，散体材料在小围压约束情况下一般会发生剪胀破坏，塑性硬化模型特别适合模拟散体材料屈服后的剪胀行为，因此本文在数值模拟中采用能够考虑土体剪切硬化和体积硬化行为的塑性硬化模型来模拟碎石桩体[13]. 图1为塑性硬化模型在三轴压缩状态中的应力应变曲线，其中偏应力曲线（图 1 （a））基于Duncan-Chang双曲线模型采用摩尔库伦强度线进行截断得到，截断的破坏比定义为Rf = qf /qa. 模型的刚度采用参数E50来定义，对应的是曲线上偏应力q = 1/2qf时的割线刚度. 参数E50满足以下关系：

E50 = Eref50Z m        （1）

其中 ：

式中：σ3为最小主应力;c为黏聚力;φ为峰值内摩擦角;m为幂指数;pref为参考压力;Eref50为与刚度相关的材料参数.

图1 （b）为塑性硬化模型的体积应变曲线，初始体积压缩段由材料的泊松比ν控制，非线性体积剪胀行为可发生在材料达到屈服强度之前，并由材料的剪胀角ψ控制. 碎石体积剪胀意味着材料从密实状态趋于疏松，因此碎石剪胀不可能无限发展，通过设置模型的最大体积应变εv，max对体积应变曲线进行截断防止碎石桩体产生过分鼓胀. 与常规摩尔库伦模型相比，塑性硬化模型能够更好地反映碎石材料的非线性应力应变关系，尤其是其考虑峰值前非线性和最大体积应变截断的剪胀行为非常适合模拟碎石等散体颗粒材料.

1.2   碎石桩单桩竖向受荷试验的数值模型

通过有限差分软件FLAC3D采用塑性硬化模型对软土中的碎石桩单桩竖向受荷的全过程进行数值模拟. 图2为刚性加载下的碎石桩单桩受荷试验的数值模型. 参考实际工程常用尺寸建模，碎石桩桩体半径rp为0.3 m，桩长为4.8 m. 由于单桩模型的轴对称特性，数值模型取实际模型的1/4进行分析. 桩体模型顶部设有与桩体尺寸一致的刚性加载板，模型基底设为刚性持力层. 模型的底部和侧面均设置简支约束，约束其法向位移. 桩土模型首先在重力作用下达到初始平衡状态后，通过以恒定速率向下移动刚性加载板对桩体施加荷载.

桩周土体采用摩尔库伦模型，设为饱和不排水状态，不考虑其固结过程. 桩体及土体的材料参数分别见表1、表2. 其中土体弹性模量选取5 MPa和20 MPa分别计算，以分析土体刚度对桩体破坏模式及承载力的影响. 在桩土界面设置不考虑厚度的接触单元，以模拟桩土相互滑移. 界面接触模型采用库伦剪切滑移模型，接触单元的剪切强度按照土体的抗剪强度进行一定折减选取，接触单元的法向和切向刚度满足关系：kn = ks = 200 × （4G/3 + K），其中G为土体的剪切模量，K为土体的体积模量. 桩土界面接触参数见表3.

1.3   碎石桩单桩承载失效全过程数值模拟

图3为刚性加载板下的碎石桩单桩荷载试验全过程的荷载沉降（p-s）曲线. 根据p-s曲线（曲线0a′b′c′）的形态可将较软土体中的整个加载过程大致分为3个阶段，分别为线弹性阶段（0a′）、非线性变形阶段（a′b′）和桩体破坏阶段（b′c′）. 不同荷载阶段所对应的土体塑性区分布见图 4 （a）. 在0a′阶段，桩周土体未发生屈服保持在弹性状态，对应的p-s曲线为直线段，a′点（s=2 cm）时桩侧少量土体单元开始出现屈服;在a′b′阶段，随着竖向荷载的增加引起桩身鼓胀从而导致桩周土体的塑性区逐渐扩大，该阶段p-s曲线的斜率逐渐增加，在b′点（s=18 cm）时桩周土体屈服区范围往侧向有了较大发展;此后在b′c′阶段，土体的塑性区逐渐向更宽和更深处发展但发展宽度不大，p-s曲线没有出现明显极限荷载但沉降迅速增大，该阶段可认为是桩体的破坏阶段.

图3中较硬土体中的p-s曲线（曲线0abc）同样可分为3个类似阶段. 3个阶段所对应的塑性区分布见图 4 （b）. 但与E = 5 MPa条件下的不同之处在于，在b点处（s = 23 cm），桩周土体的塑性区向上发展至地表，剪切应变则形成了贯通至地表的连续剪切带. b点以后的p-s曲线出现了陡降，因此可认为碎石桩在b点开始发生破坏.

碎石桩破坏后桩体及土体最终变形场、剪切应变增量云图及位移矢量分布见图5. 不同刚度土体中桩体鼓胀变形破坏的形态基本一致，也与部分模型试验研究观察到的结果十分类似[4，9，14]. 但桩周土体的变形则有较大区别，较硬土体在桩体鼓胀作用下形成了贯通地表的滑裂面，滑裂面内出现整体抬升区域，地表出现隆起变形. 而在较软土体中的变形区则维持在地表以下局部区域，且以水平位移为主，地表不出现隆起.

p-s曲线的终点对应的桩顶竖向应力即为单桩极限承载力的数值解，软硬两种土中的单桩极限承载力均与Brauns公式计算值有一定差异. 在较软土中，由于桩周土体在整个加载过程中并未形成贯通地表的连续滑裂面，与Brauns所假设的破坏模式不同，因此单桩承载力小于Brauns解. 而较硬土体中，桩周土体的破坏模式与Brauns提出的整体剪切破坏大致相同，因此单桩承载力比较接近Brauns解. 但Brauns解忽略桩侧摩阻力对单桩承载力的贡献，而数值模拟在桩土界面设置了抗剪强度，一定程度上反映了桩侧摩阻力影响，因而较Brauns解稍大.

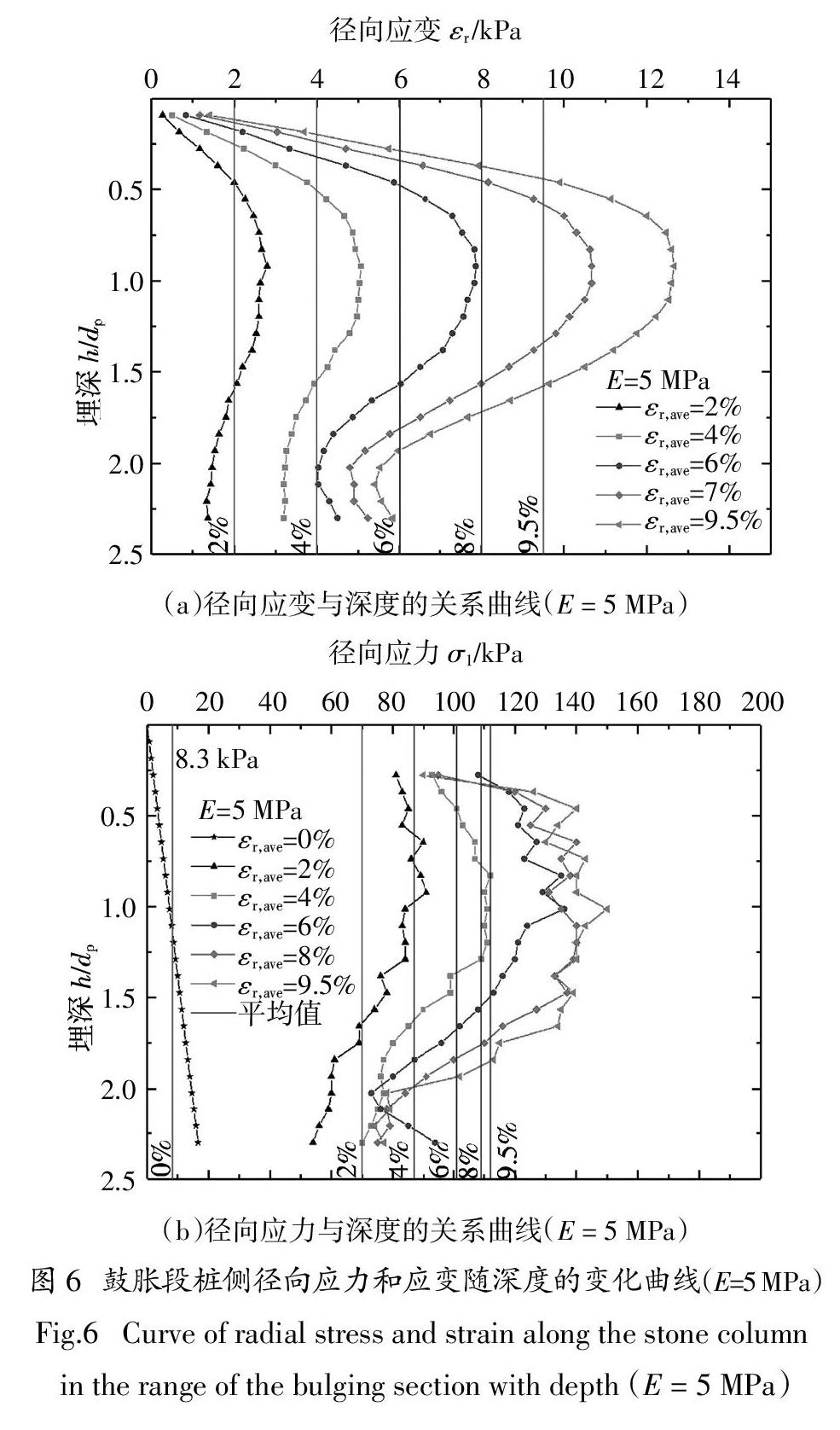
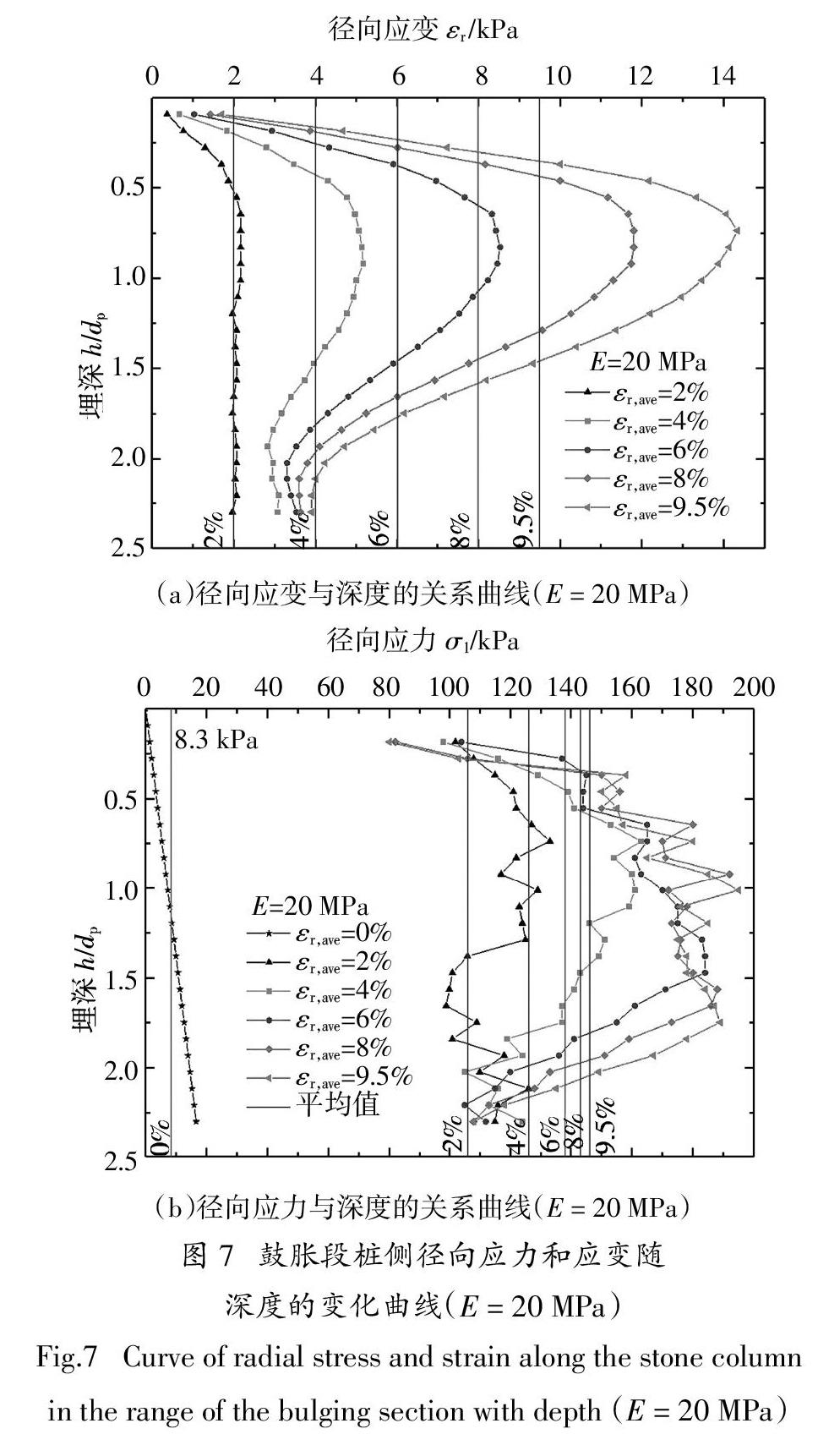
图6和图7进一步分别给出了E = 5 MPa（较软土）和E = 20 MPa（较硬土）情况下，桩体鼓胀段范围内（约2.3倍桩径）在不同荷载阶段的桩体径向应变及所受径向约束应力的分布. 为便于定量对比，两图中标出的豎直实线对应其鼓胀段范围内相应荷载阶段的应变应力的平均值. 随着荷载增加桩体径向应变也不断增加，由于鼓胀段上下部摩擦约束等原因，径向应变分布呈现上下两端小中部凸出的形态. 较软土中（图 6 （a）），各阶段的桩体最大径向应变的位置基本不变，大致位于深度1倍桩径处，最终桩体最大径向应变为12.5%. 较硬土中（图 7 （a）），桩体最大径向应变的位置轻微上移，在最终阶段大致位于深度0.75倍桩径处，其值为14.5%，大于较软土的情况. 软硬两种土中，碎石桩的剧烈鼓胀变形均集中在桩体上部距离地表2倍桩径范围内，且大小接近，说明在不同刚度土体中碎石桩体鼓胀失效模式没有变化，造成承载力差距的原因主要是土体所提供的径向约束应力不同.

图 6 （b）与图 7 （b）显示了径向应力随着径向应变的增加而增加，但由于桩周土体不断扩大屈服范围，径向应力增加的幅度不断减小并最终将趋于零. 由于土体刚度不同，较硬土径向应力增加的幅度大于较软土，最终平均径向应力也大于较软土. 由于桩体最终因为同样的鼓胀形态破坏，因此碎石桩的单桩承载力大小应取决于桩体鼓胀失效时刻鼓胀段所受到的径向约束应力.

1.4   碎石桩单桩承载失效过程参数分析

进一步通过数值模拟应力应变结果讨论土体刚度对碎石桩单桩承载模式的影响. 图8给出了土体刚度E分别为1、 5、10、 20、 30  MPa情况下，加载至桩顶沉降为25 cm时（可认为发生破坏）的数值模拟结果云图.

图 8 （a）为桩周土体的剪切应变增量云图. 当刚度E大于20 MPa后，桩周土体均形成了贯通地表的连续滑裂面，滑裂面宽度为3.7rp，深度为4.6rp，此时桩周土体发生了整体剪切破坏，与Brauns提出的破坏模式相同. 当土体的刚度较小（1～10 MPa）时，桩体产生的水平位移（图 8 （b））与较硬土体几乎一致，但由此产生的水平应力却小于较硬土. 桩周土体水平应力剧烈变化的范围主要集中在桩身上部，且随着土体刚度的增加，水平应力剧烈变化的范围逐渐增大，但发生整体剪切破坏后，剧烈变化的范围基本保持不变（图 8 （c））.

图 9 给出了不同土体刚度情况下的p-s曲线以及鼓胀段（2.3dp）平均径向应变与平均径向应力曲线图. 两组曲线显示出了一致性，随着桩周土体刚度的增大，桩侧的平均径向应力逐渐增大，对应的碎石桩的极限承载力也逐渐增大，说明桩体的极限承载力可以与桩体失效时桩体鼓胀段所受的平均径向应力建立联系.

图9还给出了相同参数下不考虑土体刚度的Brauns解作为对比，由于数值模型考虑了桩土间的摩阻力，Brauns解因而低于整体剪切破坏模式下碎石桩极限承载力的数值解. 但图 9（b）中给出的Brauns解的径向应力值则高于各刚度土体情况下的数值解. 因此，Brauns解很可能高估了低刚度土体所能提供的最大径向约束力，从而高估了碎石桩的单桩极限承载力.

在较软土体中，桩周土体刚度的提高对碎石桩极限承载力的提高作用明显. 但在较硬土中（图9中E =20 MPa及E = 30 MPa）则不明显，一旦形成了贯通的连续滑裂面后（整体剪切破坏），桩体极限承载力取决于滑裂面的形状及土体的抗剪强度而非刚度. 但当桩周土体产生局部剪切破坏（图9中E < 20 MPa）时，土体的刚度对碎石桩承载力影响十分明显，桩体极限承载力此时取决于土体刚度而非抗剪强度.

2   典型荷载沉降曲线及破坏机理

根据上节数值分析结果可以总结出图10所示的刚性荷载下软土中碎石桩单桩竖向受荷的典型荷载沉降曲线及破坏模式. p-s曲线接近直线的桩土弹性变形状态仅能在加载初期维持. 随荷载的增加，靠近碎石桩鼓胀变形最大位置（约1倍桩径处）的土体首先进入屈服状态，此时对应图10中的pcr为临塑荷载. 接下来的荷载将使桩体产生较大鼓胀变形并挤压桩周土体，导致土体塑性区向水平和竖向扩展，并引起p-s曲线偏离线性形状. 桩周土体在桩体鼓胀变形的挤压下最终可能形成贯通地表的连续滑裂面. 碎石桩则最终因为鼓胀段（约2倍桩径）径向应变无法限制（约8%～12%）而丧失承载力. 在刚度较大土体中，土体形成连续滑裂面将先于桩体的鼓胀失效. 一旦滑裂面贯通地表，土体径向应力将达到最大值不再继续增加，桩体的鼓胀变形随即迅速增大而承载失效，p-s曲线出现陡降段，这种破坏模式为整体剪切破坏模式. 在刚度较低的土体中，桩周土体的径向应力始终缓慢增加，直到桩体发生鼓胀失效也没有达到其抗剪强度对应的最大值，p-s曲线表现为斜率始终缓慢增加但没有明显突变点. 桩周土体在桩体失效时无法形成贯通地表的连续滑裂面，这种破坏模式为局部剪切破坏模式.

碎石桩鼓胀变形与桩周土体径向应力增长是一个相互协调的过程. 当土体抗剪强度相同时，局部剪切破坏模式下桩体失效时对应的桩周土体径向应力小于整体剪切破坏模式，因此最终承载力也小于整体剪切破坏模式. 目前碎石单桩承载力计算方法所假定的整体剪切破坏模式仅发生在刚度较大的土体中. 而在较软土中将产生局部剪切破坏，因此碎石单桩极限承载力的计算有必要考虑土体刚度的影响. 由于两种破坏模式下的碎石桩单桩极限承载力均取决于桩体鼓胀失效时对应的桩周土体的径向应力大小，因此有必要确定碎石桩自身的鼓胀失效状态.

在两种模式下达到破坏时所对应的桩顶沉降也有区别. 较软土体中由于土体刚度较小，径向应力增长缓慢，碎石桩无法获得有效约束因而产生更大沉降. 在相对较硬的土体中则相反，但当土体滑裂面贯通时，径向应力将无法增长，因而桩体鼓胀变形迅速增大并破坏. 因此，局部剪切破坏模式的沉降是“渐进式”的，而整体剪切破坏模式的沉降具有“突变式”的特点.

3   碎石桩单桩竖向承载力求解

3.1   计算模型及假定

通过前述碎石桩单桩承载机理可知，软土中的碎石桩单桩承载力计算有必要考虑桩体鼓胀变形、桩周土体刚度对最终径向约束力的影响. 软土中单桩桩体鼓胀变形与弹塑性介质圆孔扩张理论中的圆孔径向应力应变关系有较高相似性，因此本节基于圆孔扩张理论对软土中碎石桩单桩的极限承载力计算公式进行推导.

基于圆孔扩张理论的桩体侧限约束计算模型如图11所示，并考虑基本假定：1）桩周土体为内半径R0、外半径半无限大的筒体，变形受力过程视为平面应变问题;2）桩体上部的鼓胀变形段长度为hp = 2rp tan δp，其中rp为桩体半径，δp = 45° + φp /2，φp为桩体的内摩擦角;3）桩周土体为均匀、各向同性的弹塑性材料，塑性区土体服从小应变理论和Mohr-Coulomb强度准则，采用不排水抗剪强度;4）加载之前，整个土体具有各向同性的有效应力，不考虑体力作用. 在受力变形过程中，桩周土体的应力状态可划分为图11所示的3个区域：a）塑性区为Ru ≤ r < Rp的区域;b）弹性区为Rp≤ r < Re的区域;c）原土应力区为Re ≤ r < R∞的区域.

3.2   桩侧径向约束应力计算

根据弹性力学原理，弹性区土体的应力场由拉梅解答可得：

即弹性区内应力场满足：

式中：σr为径向應力;σθ为切向应力;Pu为孔内压力.

根据弹性理论可得径向位移u表达式为：

则在弹性区和塑性区边界上的径向位移up为：

式中：ν为泊松比;E为弹性模量;cu为黏聚力.

对于塑性区可列出平衡方程：

且需满足塑性屈服条件：

σr - σθ = 2cu           （8）

联立式（7）（8）可得：

在弹性区和塑性区边界上需要分别满足式（4）和式（8），可得：

σrp = cu                       （11）

代入式（9）可得孔内壁压力表达式：

若假定塑性区在小变形下保持体积不变，则：

πR2u - πR20 = πR2p - π（Rp - up）2           （13）

（Ru - R0）（Ru + R0） = 2Rp up - u2p          （14）

略去u2p和u2r，孔内壁径向位移满足ur = Ru - R0，则可得：

将式（6）代入式（15）可得：

故孔内壁的径向应变εr为：

式中：G为土体剪切模量.

由小变形假设，可令：

将式（19）代入式（12）可得：

最后，考虑初始地应力场的作用，则最终的孔壁压力Pu见式（21），即为桩侧径向约束应力随桩体径向应变变化的计算公式：

式中：γs为土体的重度.

3.3   极限桩侧径向约束应力计算

如图1（b）所示，碎石材料在荷载作用下发生剪胀使得密实程度降低，因此碎石材料桩体存在最大的体积应变εv，max. 同样碎石桩体不可能持续产生无限制鼓胀变形，当鼓胀发展到一定程度时的桩体将丧失承载力，因此碎石桩单桩承载失效时应当存在标志着失稳的径向应变极限值εr，max，该值与碎石三轴试验曲线中最大体积应变εv，max揭示着相同的散体材料物理临界状态. 因此桩体承载力大小可由径向应变极限值εr，max对应的径向约束力决定，软土中碎石桩单桩竖向极限承载力Pp为：

式中：εr，max为鼓胀段平均径向应变的极限值，主要与碎石密实程度及围压相关，可以由碎石桩体模型试验及碎石室内试验获得. 部分相关研究观察到εr，max处于8%～12%之间[15-16].

式（22）的承载力计算公式考虑了桩体鼓胀变形、桩周土体刚度、土体的抗剪强度以及初始自重应力的影响，能够较好地反映局部剪切破坏模式中的承载机理. 但式（22）在径向应变极小时可能出现负值而不再适用（εr ≤ 0.5e-1cu /G）. 下节将通过承载力数值解验证该承载力计算公式的有效性.

4   承载力公式数值验证

图12为加载全过程的数值径向应力应变曲线与Brauns解以及本文解的对比. 从图中可看出当土体刚度较小时，数值解的最终径向约束应力远小于Brauns解. 本文的径向约束应力解（式（21））与数值结果在各级土体刚度情况下均吻合良好，能够正确反映局部剪切破坏模式下桩体径向应力与径向约束应力的关系. 在E = 1 MPa时径向应变較小区域本文解低于数值解，原因是式（21）在低刚度土体且径向应变极小时出现负值，但随着径向应变增加本文解与数值解趋于一致. 在E = 30 MPa时本文解与数值解在桩体破坏后出现差异，主要是由于数值解在模型刚度较大时发生类似脆性破坏引起数值不稳定.

图13为数值p-s曲线与Brauns解以及本文解（式（22））的对比. 本文单桩极限承载力解在各级土体刚度下均低于承载力数值解，这是因为本文解未考虑桩侧摩阻力的影响，但两者的差距随着刚度的增大而逐渐减小. 本文解随着土体刚度增加而逐渐接近Brauns解，说明本文提出的方法也适用于计算整体剪切破坏模式下的单桩极限荷载.

5   结   论

本文将塑性硬化模型应用于碎石桩体，对软土地基中碎石桩单桩竖向受荷破坏全过程进行数值模拟，分析了桩体鼓胀段的变形过程及桩侧土压力的变化过程，重点研究了桩周土体刚度的影响，总结了典型荷载沉降曲线及破坏机理，基于圆孔扩张理论推导了软土地基中碎石桩单桩的承载力计算公式，得出以下结论：

1）软土地基中碎石桩单桩变形破坏过程分为3个阶段：线弹性阶段、非线性变形阶段和桩体破坏阶段. 破坏模式取决于桩周土体的刚度，传统承载力计算假设的整体剪切破坏模式仅发生在刚度较大的土体中，通常软土更容易产生局部剪切破坏模式. 局部剪切破坏模式的沉降变形是“渐进式”的，而整体剪切破坏模式具有“突变式”的特点.

2）整体剪切破坏模式下，碎石桩单桩承载力主要取决于土体的抗剪强度及破坏面的形式，而局部剪切破坏模式下，碎石桩单桩的承载力主要受桩周土体刚度的控制，与土体抗剪强度关系不大.

3）本文根据圆孔扩张理论建立的软土地基中的碎石桩单桩竖向承载力公式与数值解在各级土体刚度情况下均吻合良好，能够正确反映局部剪切破坏模式;通过选取合适径向应变极限值，本文解也接近Brauns解，说明本文提出的方法同样适用于整体剪切破坏模式.

参考文献

[1]    刘杰，赵明华，何杰. 碎石桩复合地基承载及变形性状研究[J]. 湖南大学学报（自然科学版），2007，34（5）：15—19.

LIU J，ZHAO M H，HE J. Research on bearing and deformation characters of composite foundation with granular columns[J]. Journal of Hunan University （Natural Sciences），2007，34（5）：15—19. （In Chinese）

[2]    肖成志，夏博洋，郑刚，等. 基础埋深对碎石桩复合地基桩体破坏模式的影响[J]. 重庆大学学报，2019，42（7）：63—69.

XIAO C Z，XIA B Y，ZHENG G，et al. Influence of composite foundation embedded depth on the failure modes of stone columns[J]. Journal of Chongqing University， 2019， 42（7） ： 63—69. （In Chinese）

[3]    赵明华，何玮茜，刘猛. 基于圆孔扩张理论的碎石桩承载力计算方法[J]. 水文地质工程地质，2017，44（3）：55—60.

ZHAO M H，HE W X，LIU M. Calculation method for the bearing capacity of stone columns based on the cavity expansion theory[J]. Hydrogeology & Engineering Geology，2017，44（3）：55—60. （In Chinese）

[4]    HUGHES J M O，WITHERS N J. Reinforcing of soft cohesive soils with stone columns [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts，1974，11（11）：A234.

[5]    BRAUNS J. The initial load of gravel pile in the clay foundation[J]. The Construction Technology，1978，55（8）：263—271.

[6]    WONG H Y. Field instrumentation of vibroflotation foundation[J]. Field Instrumentation in Geotechnical Engineering，1974，23（4）：475—487.

[7]    郑刚，周海祚，刁钰，等. 饱和黏性土中散体桩复合地基极限承载力系数研究[J]. 岩土工程学报，2015，37（3）：385—399.

ZHENG G，ZHOU H Z，DIAO Y，et al. Bearing capacity factor for granular column-reinforced composite ground in saturated soft clay[J]. Chinese Journal of Geotechnical Engineering，2015，37（3）：385—399. （In Chinese）

[8]    贾尚华，赵春风，赵程. 砂土中柱孔扩张问题的扩孔压力与扩孔半径分析[J]. 岩石力学与工程学报，2015，34（1）：182—188.

JIA S H，ZHAO C F，ZHAO C. Analysis of expanded radius and internal expanding pressure of cylindrical hole[J]. Chinese Journal of Rock Mechanics and Engineering， 2015， 34（1） ： 182—188. （In Chinese）

[9]    谭鑫，赵明华，金宇轩，等. 碎石桩单桩受荷模型试验的离散單元法数值模拟[J]. 湖南大学学报（自然科学版），2019，46（3）：106—113.

TAN X，ZHAO M H，JIN Y X，et al. Numerical simulation of loading test on a single stone column using discrete element method[J]. Journal of Hunan University（Natural Sciences），2019，46（3）：106—113. （In Chinese）

[10]  TAN X，ZHAO M H. Deformation and failure behavior of the isolated single stone column with and without geosynthetic encasement[C]// Proceedings of the 2nd International Symposium on Asia Urban GeoEngineering. Changsha，2018：547—559.

[11]  谭鑫，曹明，冯龙健，等. 土工织物包裹碎石桩力学特性的数值模拟研究[J]. 中国公路学报，2020，33（9）：136—145.

TAN X，CAO M，FENG L J，et al. Numerical study on mechanical behaviors of geotextile-wrapped stone column[J]. China Journal of Highway and Transport，2020，33（9）：136—145. （In Chinese）

[12]  陈建峰，韩杰. 夯扩碎石桩单桩载荷试验数值模拟[J]. 岩土工程学报，2009，31（9）：1366—1370.

CHEN J F，HAN J. Numerical modeling of loading tests on a rammed aggregate pier[J]. Chinese Journal of Geotechnical Engineering，2009，31（9）：1366—1370. （In Chinese）

[13]  SCHANZ T，VERMEER P A，BONNIER P G. The hardening soil model：Formulation and verification[C]//Beyond 2000 in Computational Geotechnics. Routledge，2019：281—296.

[14]  SHIVASHANKAR R，DHEERENDRA BABU M R，NAYAK S，et al. Experimental studies on behaviour of stone columns in layered soils[J]. Geotechnical and Geological Engineering，2011，29（5）：749—757.

[15]  PETER K. Soil structure interaction and group mechanics of vibrated stone column foundations[D]. South Yorkshire，England：University of Sheffield，2014：167—200.

[16]  ALI K，SHAHU J T，SHARMA K G. Model tests on geosynthetic-reinforced stone columns：a comparative study[J]. Geosynthetics International，2012，19（4）：292—305.