基于NSGA-II和SVDD的转向架构架异常状态监测*
李 鹏,黄培炜,丁 瀛,杜艺博,彭嘉潮
(华东交通大学机电与车辆工程学院,江西 南昌 330013)
转向架构架是列车的关键承载部件,具有传递列车主要载荷、固定车轴位置的作用,其健康状态极大地影响了列车运行安全。2017年12月,日本新干线“希望34号”列车转向架出现14cm长裂纹,被定为“严重”事故。近年来,针对转向架构架的状态监测研究已得到了广泛的关注[1-3]。高云霄等人通过分析构架关键测点动应力和载荷应力的传递关系,实现了构架侧滚、蛇形失稳和扭转等状态的识别,一定程度上弥补了测力构架法成本高昂过程复杂的不足[4]。张楠等人通过基于频率响应函数的传感器分布优化方法,探索了利用有限数量传感器获取有效转向架构架振动信息的方法[5]。Jun-Sung Goo等研究城市列车行驶时由道碴飞扬现象引起的玻璃纤维增强树脂基复合材料转向架结构完整性问题,研究通过获取复合材料转向架在飞碴冲击下的残余应力和应变信息,对损伤后的复合转向架构架进行静力分析并评价结构完整性[6]。
目前,构架状态监测建模中面临的异常状态复杂多样性,以及监测中传感器的分布优化问题已引起了广泛的重视。而各种传感器分布优化方法其主要区别是在优化目标函数和优化算法的选择上[7-9],优化目标函数和优化算法的选取对传感器分布优化结果的有效性及计算的复杂性具有重大影响。因此,如何定义优化目标函数,并通过布置更少的传感器,获取更多的结构有效响应数据和特征,对于工程应用具有重要意义。
研究针对构架异常状态下样本集的随机多样和不确定性,引入支持向量数据描述(support vector data description,SVDD)算法,以构架正常状态的样本集构建SVDD超球体模型对多工况条件下构架的异常状态进行识别。同时基于改进的非劣分层多目标遗传算法(non-dominated sorting genetic algorithm II,NSGA-II)对传感器分布进行了优化[10]。
1 状态监测对象
研究以209型转向架构架为对象,旨在通过传感器分布优化,实现对构架健康状态的有效监测。研究基于相似原理[11],采用相同的材料(Q235A钢),按5:1尺寸比制备构架结构模型,如图1所示。

图1 构架结构模型
209P型转向架用于客车或货车居多,在实际运行中,25G型客车上的转向架构架发生异常率较高与其他车型。当客车车体平稳经过铁轨,转向架及其构架在相对稳定下运行,转向架构架主要受静载荷的影响产生形变。如图2(a)所示,209型客车转向架构架通过摇枕与车体相连接,承受车体的重力。轮对通过导柱支撑板与构架衔接,对构架提供支撑力。构架所受载荷如图2(b)所示,F1a、F1b、F2a、F2b对应导柱支撑板提供的支持力;A、B、C、D点上FA、FB、FC、FD对应车体通过摇枕施加在构架上的车体重力。

图2 构架结构模型所受载荷图
由于构架主要承受垂直方向上的力,因此将构架水平方向表面作为传感器布置面,传感器备选点应尽可能覆盖整个构架,同时结合实际工程经验,同类转向架构架常见裂纹部位主要集中在构架端梁弯角处、构架上各吊座焊接处以及横梁两端与侧梁结合的弯角处[12]。如图3所示,在构架上均匀分布的14个传感器备选点,用于安装传感器获取应变响应。

图3 传感器备选点编号
2 优化目标
传感器分布优化的目标是通过优化传感器的位置,以较少数量的传感器实现对构架健康状态的有效监测,研究据此设计双目标优化函数f1和f2。
2.1 目标函数f1:传感器数量
目标函数f1—传感器数量是指布置于构架上的传感器个数,有效地减少传感器数量,不仅可以降低监测系统的成本,而且有利于加快数据的处理速度,提高监测系统的实时性[13]。

2.2 目标函数f2:超球体聚类指标最大化
支持向量数据描述算法提供了一种采用超球体进行样本集边界定义的方法[14]。研究考虑到构架异常状态下样本集的随机多样和不确定性,期望通过优化正常状态样本识别正确率B获得能有效包含构架正常状态样本集的超球体最小半径,进而定义目标函数f2。
SVDD算法通过内核函数使样本集周围形成超球体边界[15],其结构误差ε定义为:

对于SVDD构建的超球体而言,好的超球体边界描述应包括所有目标样本,但不包括多余的空间。由此可得到最小化约束条件:


由式(4)可求出超球体中心o的最优解:


对于新样本→Y→S:

假设构架在p种工况的正常状态下的样本数为p×a,a为构架每个工况下的正常状态的样本数。在a中随机取b个用于SVDD建模,其余作为评价样本,用于量化目标函数f2,同时以特征维数m为权值,则目标函数f2可表示为:

3 非劣分层遗传算法优化
研究中传感器分布优化目标函数包括f1—传感器数量和目标函数f2—超球体聚类指标,属于双目标优化问题,两个目标函数在优化过程中相互冲突和影响,存在优化方向非一致问题,即随着f1的增大,f2也会增加无法获得最优解。因此,研究引入非劣分层思想,基于遗传算法获取满足优化目标的传感器分布非劣解集[17]。
NSGA-II是一种基于最优保存策略的随机寻优算法[18],其本质是模拟自然中生物进化的过程,遵循物竞天择的原则,个体优势基因将有更大机会传递下去,同时加入一定的变异概率,从而可以避免陷入局部最优解,找到全局最优解。具体步骤如下:
步骤1 设定个体编码方式
传感器分布方案采用A维列向量→S表示,→S中元素Sk取值1(或0)表示第k个待优化传感器备选点有(或无)传感器。图4为一种传感器分布方案的编码,表示在传感器4和7号备选点放置有传感器。

图4 传感器分布方案编码
步骤2 设定优化参数
设定迭代次数T,交叉概率pc,变异概率pm。
步骤3 创建初始种群
随机生成规模为n的初始种群:
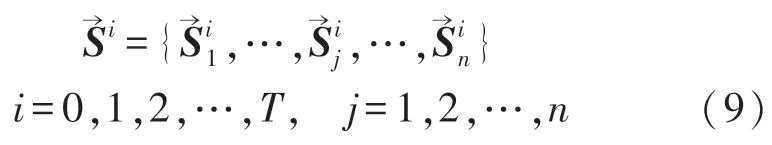
式中:i为0时表示初始种群,T为迭代终止次数,j表示种群中个体的编号。
步骤3 建立优选池
由式(1)和式(8)计算种群中所有个体的目标函数f1和目标函数f2的值,据此对所有个体进行非劣层级划分,并采用轮盘赌从父代中挑选n个个体放入优选池Mi′。
步骤4 生成交叉种群
每次随机从Mi′中选择2个个体,按随机生成的交叉点对两个个体进行交叉操作,交叉种群Mi″规模为n×pc。
步骤5 生成变异种群
每次随机从Mi′中选择1个个体,按随机生成的变异点对该个体进行变异操作,变异种群Mi″规模为n×pm。
步骤6 生成子代
将优选池、交叉种群和变异种群合并,并根据目标函数f1和目标函数f2的值对合并后的种群进行非劣层级划分,将非劣层级最前和拥挤距离最大的n个个体放入子代Si+1。
步骤7 迭代终止条件
①将Si+1同Si第一非劣层级中的个体进行比较,出现连续100次迭代结果相同时,则迭代结束;
②迭代次数达到10 000次,迭代结束。
4 实验验证
4.1 多工况下构架正常状态样本集采集
对于一节客车车体而言,209P型转向架的技术参数如表1:

表1 209P型转向架基本参数
研究采用其一节车厢空载时质量mc=48.6 t,并假设列车正常平稳运行时车体质量在两个转向架中心均匀分布,车体重力由摇枕左侧A、B两点和右侧C、D两点均匀承担。由图2和表1可得:
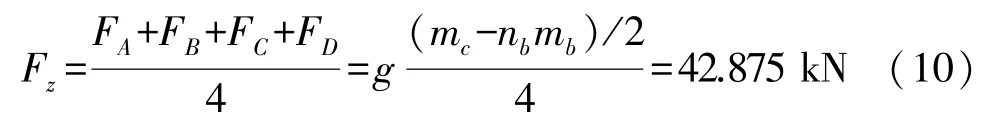
式中:Fz为A、B、C、D各点上所受载荷力均值。在此基础上,依据《TB/T 2368-2005动力转向架构架强度试验方法》[19]中的垂向载荷工况,结合常规运行条件下车体侧滚和车体垂向运动(浮沉)引起的垂向力动态变化,设置了5种正常运营工况(如表2)。表2中侧滚系数φ取值0.15,浮沉系数φ取值0.25。

表2 模拟构架运营载荷工况组合表
构架结构模型采用图1所示模型,载荷按25∶1等比例缩小[8]。考虑到客车正常运营过程中载重会变化,以工况1为例,取整车车厢质量波动范围约为49 t~69 t,由式(10)计算工况1下两侧梁4个测点载荷范围为1 715 N至2 701 N,以34 N为间隔均分为30个载荷样本。全部工况下各测点的载荷如表3中所示(共150种正常状态)。

表3 模拟构架运营载荷工况组合表(具体值)
施加载荷的方式为:将构架反置于千斤顶上,通过四个拉力绳将其固定于花岗岩底座;千斤顶产生的力模拟为一节车体的重力,拉力绳产生的拉力作为轮对支撑板对构架的支持力,压力传感器和压力显示仪用于监测千斤顶施力的大小。整个应变监测实验平台如图5,主要的设备参数如表4所示。

图5 应变监测实验平台

表4 实验设备参数
根据表3,每种工况包含30个不同的载荷样本,则对于反映构架应变的信号矩阵S为:

式中:p表示有多少种工况,A为传感器备选点总数,c为每种工况下对应不同载荷的应变数据。即Sk为第k个传感器备选点对所有工况的响应信号矩阵,S为所有传感器备选点对所有工况的响应信号矩阵。
4.2 传感器网络优化结果
在NSGA-II算法中设置好初始参数,迭代终止次数T=1 000,交叉概率pc=0.3,变异概率pm=0.2,初始种群个数n=200,和传感器备选位置总数A=14。经优化后的传感器分布非劣解集如表5所示。

表5 传感器分布优化结果
4.3 多工况下构架异常状态识别
根据相似原理,同样以25∶1的比例将日本新干线上列车转向架的14 cm长裂纹进行缩小,在构架模型横梁与侧梁连接处加工一道约深5 mm、宽1 mm的裂纹,裂纹位置[20]和裂纹细节如图6所示。根据传感器分布优化的结果,用搭建好的应变监测实验平台获取构架有裂纹状态下在不同工况的异常状态响应数据。除增加一道构架裂纹外,异常状态的载荷工况与构架正常状态的一致(共150种异常状态),同样采用表3作为其载荷工况组合进行载荷施加,获取每种工况下的30个不同载荷样本。

图6 构架模型结构裂纹位置示意图
采集设备与采集正常状态下构架的应变响应数据的设备一致,步骤一致,根据式(11)其采集到的构架异常特征响应数据为:

式中:p′表示有多少种工况,c为每种工况下对应不同载荷的应变数据,A*′为同一非劣层级下不同传感器网络中传感器的个数,k*′为对应的传感器网络中的传感器备选点位置。对于第1非劣层中应变传感器网络而言{A*′=1,2,3},{k*′=[8],[6、7],[6、7、8]};对于第2非劣层中应变传感器网络而言{A*′=1,2,3},{k*′=[7],[6、8],[6、8、9]}。
用于测试的构架异常状态数据集如式(12)所示。根据式(11),提取优化后应变传感器网络对应的构架正常状态数据集,用于SVDD建模,如下式所示:

将优化后应变传感器网络对应的构架正常状态数据集,并代入SVDD参数(罚参数C,核参数σ;C=0.25,σ=16),建立超球体模型,进行多工况多载荷状态下的构架异常状态识别,识别流程如图7所示。

图7 构架状态监测流程
根据优化后的应变传感器网络对于第1非劣层的应变传感器网络,以及对于第2非劣层的应变传感器网络识别效果如表6所示。

表6 不同传感器网络下构架异常识别效果
实验结果与分析:
①对于应变传感器网络,当采用第1非劣层的传感器布置位置时,构架异常状态识别精度分别为:15.33%,88.67%,91.33%。结果表明,对于优化后的传感器网络,对构架异常状态的识别效果都随着传感器数量的增加而改善,验证了传感器优化网络的合理性。
②对于应变传感器网络,当采用第2非劣层的传感器布置位置时,构架异常状态识别精度分别为:9.33%,79.33%,82.00%。结果表明,对于优化后的传感器网络,均比采用第1非劣层的传感器布置位置时,构架异常状态识别精度要低,且当传感器数量f1不变时,异常状态识别精度与超球体聚类指标f2相关联。
③对比1、2、3个传感器的第1非劣层的布置方式和第2非劣层的布置方式。可以看出,在研究中,相比于超球体聚类指标f2,传感器数量f1对构架异常状态识别精度的影响更大。
5 结论
针对转向架构架状态监测建模面临的异常状态复杂多样性及监测中传感器的分布优化问题,研究针对构架异常状态下样本集的随机多样和不确定性,引入SVDD算法,以构架正常状态(共150种)的应变样本集构建SVDD超球体模型对多工况多载荷水平条件下构架的异常状态(共150种)进行识别。同时以SVDD超球体半径定义优化目标函数f1(传感器数量)和f2(超球体聚类指标),并基于NSGA-II算法对传感器分布进行了优化。在此基础上,搭建转向架构架状态应变监测实验平台,对多工况条件下构架的异常状态识别进行研究。结果表明:
①经NSGA-II优化后的传感器分布方案能以较少的数量保证很好的构架异常状态监测效果,研究表明当传感器分布优化方案中传感器数量为3个时,异常状态识别率已达到91.3%。
②以转向架构架正常状态样本集构建的SVDD模型对异常状态具有很好的识别效果,较好的解决了构架异常状态下样本集的随机多样和不确定性问题。

