基于LC谐振电路的智能配送无人机设计*
吴建锋,徐振宇,秦会斌
(1.浙江树人大学信息科技学院,浙江 杭州 310015;2.杭州电子科技大学电子信息学院,浙江 杭州 310018)
随着经济的飞速发展与人民生活水平的提高,各种新型餐饮形式层出不穷[1],与此同时人口老龄化比例不断上升[2],劳动力成本提升等问题也接踵而来[3],这导致我国对服务型智能机器人的需求十分迫切,我国服务型机器人市场潜力巨大[4]。
近年来代替服务员的配送机器人逐渐进入市场,市场上餐机器人路径的识别通常使用激光,摄像头和电荷耦合器件(CCD)等传感器,这些传感器容易受到外界环境中的强光干扰,导致传感器感应能力下降,给机器人也带来许许多多的问题,比如路径偏差[5],与顾客发生碰撞等[6]。
为克服上述的一系列问题,此本文设计了一款基于电磁检测的无人机,采用四轴飞行器作为载体,利用LC谐振电路检测电磁信号。通过四轴飞行器作为载体的空中的方式可以避免影响餐厅内顾客的行走与就餐[7]。此外路径上的谐振信号的频率可以设定或改变,选择一个合适的谐振信号可以避免外界干扰源对谐振信号的干扰,从而提高了循迹过程的稳定性,保证了顾客的安全[8]。
1 配送无人机的总体架构
无人机采用四轴飞行器的形式,以STM32作为主控制器,同时搭载惯性传感器、WiFi通信模块、超声波测距模块以及电调和电机。惯性传感器将采集到的数据传送给微处理器,由姿态算法实时估计出无人机的飞行姿态。根据获得的姿态信息,使用串级模糊PID控制算法,通过电调调节电机转速从而控制无人机的飞行速度和方向[9]。RFID读写模块,用于无人机的定位,通过读取预先安置的RFID标签来确定无人机的起点和终点。超声波测距模块用来测量检测障碍物,防止无人机发生碰撞。WiFi模块用于和控制中心通信,收发指令和数据。
无人机通过循迹模块检测预设的电磁信号,该信号为20 kHz的交流信号,根据检测到信号的路径,控制无人机飞往目标位置。循迹模块主要由2部分组成,一个是LC谐振电路,另一个是信号处理电路。LC谐振电路用于检测交流信号所参数电磁信号[10],无人机上共装有三路LC谐振电路,中间路的LC谐振电路用于检测信号路径的强度,判定无人机偏离轨道的程度,左右两路分别用于判断无人机偏离的方现和偏离方现的程度。此外,由于谐振电路产生的感生电动势较小,且为交流信号,无法利用A/D采样直接进行处理。因此,使用一个信号处理电路需要包括放大电路和检波电路,通过放大电路对信号进行放大,再将放大后的交流信号转换成直流信号由高精度的A/D进行采用并将信号传输至STM32微控制器进行处理[11]。
电源模块由22.2 V的动力锂电池提供总电源,转换成系统所需的各种电压,系统结构框图如图1所示。

图1 系统结构框图
2 软件设计
2.1 姿态解算
无人机的姿态指的是无人机的机体坐标系与惯性坐标系之间的角位置关系,表示这种关系的方法有多种,其中四元数法比较适合用作姿态解算,不会发生万向节死锁,且计算量小,只需要求解4个参数,在实际应用中最为广泛[12],同时也是本文所采用的方法。
姿态解算的数据由惯性传感器提供,无人机采用MPU6050传感器芯片,它是一款6轴传感器芯片,集成了一个3轴陀螺仪和一个3轴加速度计。陀螺仪用来测量无人机的3轴旋转角速度,可以通过角速度的积分来估计当前的姿态角,短时间内比较准确,但误差会随时间累积。加速度计测量无人机的3轴加速度,测量值不会受时间变化影响,但由于加速度采集到的信号噪声比较大,单纯的使用加速度计同样也会存在误差[13]。因此必须将两者的数据结合起来,才能得到较为准确的姿态信息。本文采用一种基于四元数的互补滤波进行姿态解算,基本框图如图2所示。

图2 四元数互补滤波
首先将惯性坐标系中的重力加速gn归一化后,转换到机体坐标系上得到gb,如式(1)所示,其中为方向余弦矩阵,如式(2)所示。
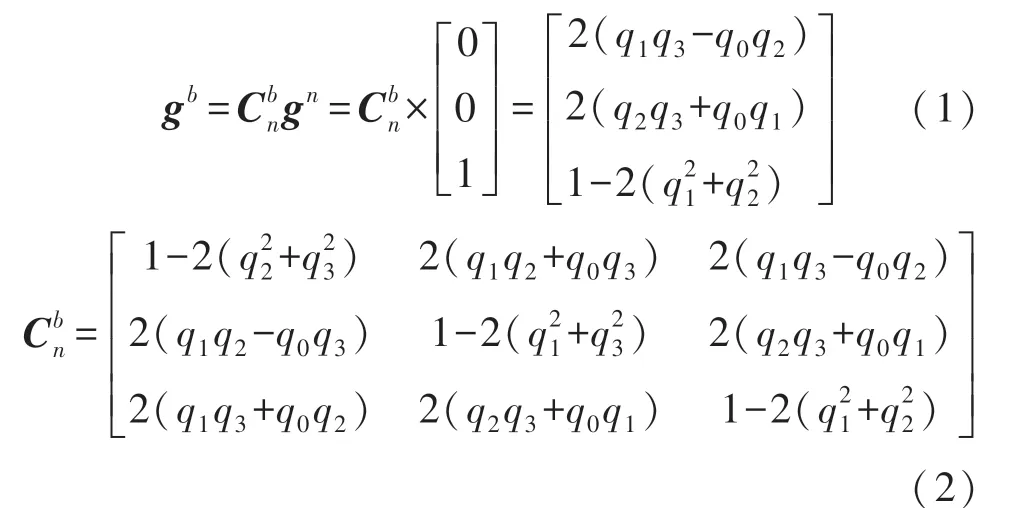
将加速度计的测量值与gb进行矢量叉乘,得到修正误差,即从加速度计测量矢量到由方向余弦推算到的矢量之间需要旋转修正的补偿误差。q0、q1、q2和q3为四元数的四个元素。
为了实现稳态控制并消除长时间累积误差,采用比例-积分控制器来对该误差进行处理,如式(3)所示:

式中:ω0(t)为陀螺仪测量值,ω(t)为修正后的值,e(t)为误差,Kp和Ki分别为比例和积分系数,用来调节加速度计信息和陀螺仪信息之间的权重。
四元数采用龙格库塔法进行更新,如式(4)所示:
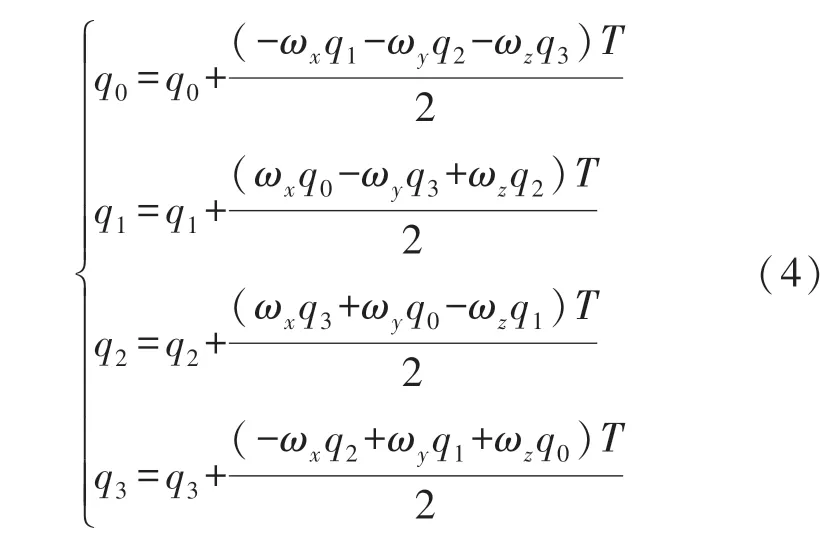
式中:ωx、ωy和ωz是经过加速度计补偿的陀螺仪的测量值,T为采样间隔时间。
将得到的新四元数进行归一化处理,计算出欧拉角和方向余弦矩阵并进入下一次迭代,计算方式如式(5)和式(1)所示:

式中:φ表示滚转角、θ表示俯仰角、φ表示偏航角。
2.2 串级模糊PID控制算法
PID控制算法是经典控制理论中常用的一种控制方法,它可以分成3个部分,分别是比例、积分和微分控制。比例控制根据输出反馈值和输入值之间的差,按照一定的比例进行调节,但是纯比例控制会存在静态误差,因此增加积分控制部分,提高控制精度,微分控制则可以实现系统的超前调节,提前减小控制输入量,减少甚至消除超调现象[14]。位置式PID控制算法计算表达式如式(7)所示:

式中:Kp、Ki和Kd分别为比例、积分、微分系数,e(t)为输入和输出反馈的误差,u(t)为调节量。
为了提高PID控制器的稳定性和响应速度,对经典PID控制器进行改进,增加模糊控制器来调节PID系数,改进的模糊PID控制器[15]控制原理如图3所示。

图3 模糊PID控制算法
PID参数Kp、Ki和Kd的计算方式如式(7)所示:

Kp0、Ki0和Kd0为初始值,经过模糊控制系统后得到实际参数,ΔKp、ΔKi和ΔKd能够在一定程度上对参数进行调节,但调节的范围受限,不够灵活,因此在此基础上,引入系数α和β,提高调节范围,并实现积分分离,防止发生积分饱和。
误差e和误差变化量Δe作为模糊控制器输入,ΔKp、ΔKi和ΔKd、α和β作为输出。e、Δe、ΔKp、ΔKi和ΔKd的模糊子集为{NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)},采用7个量化等级,论域为{-3,-2,-1,0,1,2,3}。α和β的模糊子集为{ZO(零),PS(正大),PM(正中),PB(正大)},采用4个量化等级,α的论域为{1,1.5,2,2.5},β的论域为{0,0.33,0.67,1}。其中e、Δe、ΔKp、ΔKi和ΔKd隶属度函数如图4所示,α和β的隶属度函数与之类似。根据PID参数整定原理和方法,制定的模糊控制规则表如表1~表5所示。

表5 β模糊控制规则表

图4 e、Δe、ΔKp、ΔKi和ΔKd隶属度函数

表1 ΔKp模糊控制规则表

表2 ΔKi模糊控制规则表

表3 ΔKd模糊控制规则表

表4 α模糊控制规则表
无人机采用串级PID控制算法,其控制原理如图5所示,在无人机进行工作前,无人机将被摆放在铺设谐振电路的路径上,并使中间路的LC谐振电路获取到一个最大的输入信号作为期望信号,左右两侧的LC谐振电路分别获取两个信号用于辅助控制无人机进行飞行方向控制。图5中位置环用于控制无人机的路径追踪,防止偏移设定路径。当无人机移动路径发生偏差时,中间路的LC谐振电路信号变小,两侧的LC谐振电路信号分别增大和减小,从而可以判断偏移的方向和偏移的程度,将当前的中间路的LC谐振电路信号和期望信号的差值输入到位置环的PID控制,并将输出信号输入到角度环进行进一步处理。无人机的角度环用于保持无人机的角度,并控制无人机的移动方向,无人机的角速度环用于操控无人机的速度和平衡度。因此位置环的输出和当前角度的反馈信息共同控制无人机的移动方向并使无人机保持平衡,在此过程中通过角速度环控制电机的转速,使无人机平稳的返回路径,并按照一定速度按照路径进行移动。

图5 串级PID控制算法
2.3 数字滤波算法
由于无人机在飞行过程中机体震动比较大,受其影响,传感器将会输出带有高频噪声的原始数据,这种噪声对姿态解算和飞行控制都有一定的影响[16]。因此必须通过滤波算法将引入的噪声进行滤除[17]。移动平滑滤波是一种简单的低通滤波器,它是一种从时域方面进行设计的滤波算法[18]。一般采用简单平均的方式实现,即对时域相邻采样点的数值求平均值,本系统为了避免信号采集中混入误差信号,在同一时间节点内进行20次的信号采集,默认最大的5组信号和最小的5组信号为误差信号。去除10组误差信号后面对剩余10组信号进行求平均值获得最终信号。针对原始加速度数据,采用平滑滤波算法前后对比如图6和图7所示,其中图6是原始数据,图7是经过滤波后的数据,对比图6和图7可得,图7的加速度曲线更为平滑,无人机在飞行过程中能够避免频繁的加速/减速,从而保证配送过程的稳定性。

图6 滤波前的原始数据波形图

图7 滤波后的波形图
4 实验测试
为了验证姿态解算算法以及串级模糊PID控制算法的控制效果,进行了一段时间的飞行实验,采集了无人机的俯仰角和滚转角数据如图8和图9所示。在测试的30 s内,俯仰角在(-13,15)°,横滚角在(-11,15)°,无人机在飞行过程中保持平衡。实验表明,无人机能够获取比较准确的姿态数据(俯仰角,横滚角,加速度),实现稳定飞行,具有较好的应用和推广价值。

图8 俯仰角
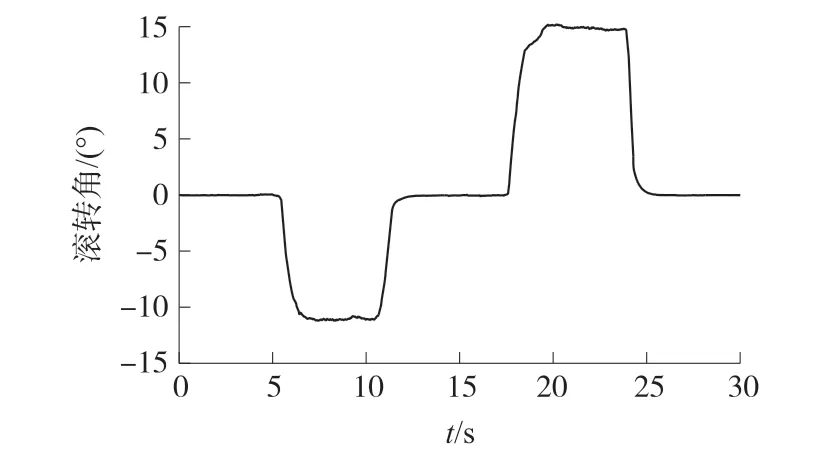
图9 横滚角
5 结论
针对传统配送机器人在配送过程中出现路径偏差,碰撞顾客等问题,提出了一种基于电磁检测的无人机,通过LC谐振电路对电磁信号进行检测,能够获得正确的路径信息,并利用一种基于四元数的互补滤波算法进行姿态解算,改进的模糊PID控制算法进一步提高了可无人机的稳定性和响应速度。实验表明该无人机能够稳定、可靠的完成任务。

