基于波场互相关的探地雷达快速自聚焦成像
杨忠委 郭聪隆 孙浩然 兰 天 杨小鹏
(1. 北京理工大学信息与电子学院, 北京 100081; 2. 北京理工大学重庆创新中心, 重庆 401120)
1 引言
探地雷达偏移成像技术通过改变雷达回波中能量的分布情况,可以更为直观地表现出地下场景及其中目标的几何或物理特征,大幅降低了目标检测和识别的难度,便于目标解译工作的开展。伴随着雷达成像技术的飞速发展,国内外学者提出了许多探地雷达偏移成像算法,并取得了很好的应用效果[1-2]。但这些算法均是建立在介质参数已知的条件下,当介质参数未知时,将会产生成像散焦和深度偏移等问题。为解决此类问题,国内外学者研究了介质参数测量方法[3-5]。Ahmad等基于高阶统计特性提出了一种自聚焦成像算法,当介质参数估计误差较小且目标处于远场区时能够取得很好的自聚焦成像效果[6]。崔国龙等提出了用于时分MIMO穿墙雷达的后向投影成像算法,通过建立介质参数已知条件下的目标回波模型,使用费马定理和斯涅耳定律计算聚焦补偿量,然后通过后向投影算法获得高质量图像[7]。Dehmollaian与Sarabandi通过求解非线性优化问题得到介质参数,然后使用合成孔径成像算法来实现目标的自聚焦成像[8]。但以上这些算法往往存在计算复杂度大且稳定性差等问题。
基于逆时偏移成像的思想,本文提出了一种探地雷达快速自聚焦成像算法。由于逆时偏移不存在对波动方程的近似,允许电磁波在任意方向进行传播,能够对任意类型的电磁波场进行成像,因此逆时偏移成像算法相比其他偏移方法具有无法比拟的优越性[9-11]。传统时域逆时偏移主要分为波场延拓和成像两部分,主要过程如下。首先,将激励源信号沿时间方向延拓,得到正传波场;将天线在接收位置处接收的数据进行时间反转,然后反传播到探测媒质中去,得到反传播场。正传和反传波场通常采用时域有限差分来进行计算。然后,对正传与反传波场按成像条件提取成像值,得到单对收发天线位置(单炮)偏移结果。最后,将每一炮的偏移结果叠加起来,即得到完整的偏移图像。可以看出传统时域逆时偏移算法需要多次的正向和反向波场外推,然后应用成像条件将每个炮点的成像结果进行累加。因此时域逆时偏移需要很大的计算与存储资源,导致其并不能在实际场景中对大数据量进行实时成像处理,故并未得到广泛应用。
逆时偏移成像条件有很多种,如激发时间成像条件、上下行波振幅比成像条件、互相关成像条件等[12],其中零延迟互相关是逆时偏移最常用的成像条件,可看作收发波场之间的匹配滤波过程。基于该成像条件,本文推导了共偏移距探地雷达数据的频域逆时偏移表达式。通过应用分层介质格林函数的平移不变性,避免了多次波场外推过程,减小了对计算和存储资源的需求。考虑到实际场景中,数据采集位置并不是均匀分布,采用非均匀快速傅里叶变换将空域非均匀采样数据变换到均匀波数域,实现了频率域多个炮点成像结果的快速累加。由于所使用的成像条件为零延时互相关,因此当介质参数准确估计时,零成像时刻所得结果便是最优聚焦图像。然而当介质参数未被准确估计时,目标会出现距离向偏移、方位向散焦的问题,算法聚焦性能严重下降。从逆时偏移成像算法原理出发,这种现象可以解释为成像时刻的不准确选取。当成像时刻提前或滞后最优成像时刻,所得图像均会出现一定程度的散焦。鉴于此,所提算法向逆时偏移成像表达式中引入了时间相位补偿因子,通过计算偏移图像的熵值并使其最小化来确定补偿量。因此所提算法不需要已知精确的介质先验信息就能实现良好的自聚焦成像效果。
2 快速自聚焦成像算法
2.1 基于波场互相关的快速频域成像
基于零延时互相关成像条件的逆时偏移算法可以表示为:
(1)
其中us(·)与ur(·)分别是发射和接收天线位置处的发射信号前向递推波场与接收信号时间反转后的后向递推波场;Tmax为接收到的A扫描数据时长,r=(x,y,z)为成像网格点坐标,对于二维垂直截面和水平切片成像则网格坐标分别取r=(x,z),r=(x,y);rs为发射天线坐标,rd=(xd,yd,zd=0)是收发天线之间的坐标差值,zd=0是因为收发天线对仅在xoy平面步进移动。对每个A扫描数据进行时域逆时偏移并进行累加便得到最终成像结果I(r)。式(1)可以写成以下卷积形式:
(2)
根据卷积定理,函数卷积的傅里叶变换是函数傅里叶变换的乘积[13],则式(2)可表示为:

(3)
其中Us(·)与Ur(·)分别为前向与后向时域波场值ur(·)、us(·)的频域形式。根据电磁场理论,频域波场是分层介质格林函数与相应收发位置处激励源频谱的乘积,即:
(4)
(5)

(6)
考虑到分层介质格林函数的平移不变性,即:
G(r,rs,ω)=G(r-rs,r0,ω)
(7)
其中G(r,r0,ω)为参考坐标点r0=(0,0,0)处的频域分层介质格林函数。
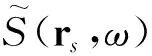
(8)
其中,
M(r,r0,ω)=G(r,r0,ω)G(r+rd,r0,ω)
(9)
在某些远场探测场景中,收发天线间距很小,式(9)可简化为
M(r,r0,ω)=G2(r,r0,ω)
(10)
可以发现式(8)是对rs+rd的卷积运算,对其应用卷积定理可得:
(11)
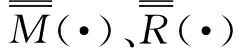
从式(11)可以看出,基于波场互相关的快速频域成像算法主要分为以下几步:
(1)根据成像场景先验信息,计算数据采集平面中心点处分层介质格林函数分布G(·);
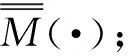
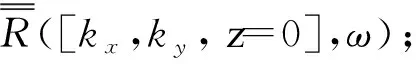

2.2 基于最小熵准则的自聚焦处理
应用上述算法的先决条件是必须精确已知介质的介电常数等先验信息,但在实际应用场景中,介质参数并非精确已知,从而导致成像结果会出现一定程度的散焦。为准确获得介质相对介电常数εr,可以通过非线性优化问题进行求解,但优化过程一般比较费时并且不稳定[6]。
为解决该问题,向式(11)引入一个时间相位因子,式(11)可以认为是成像时刻t=0的成像结果,即:

(12)
当介质参数准确估计时,则最优聚焦时刻为t=0;如果当介质参数估计误差较大,则最优成像时刻并非t=0,故将式(12)作如下修正:
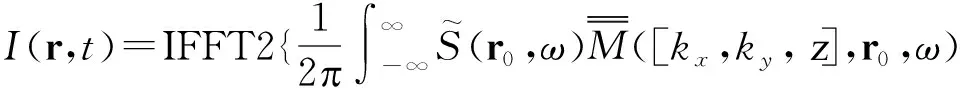
(13)
因此当介质参数估计不准确时,通过选择最优的成像时刻t,即可得到目标的最优聚焦图像,成像时刻提前或滞后最优成像时刻均会导致成像结果散焦。最优成像时刻通过最小熵准则来确定,即计算不同成像时刻的偏移图像熵值,图像熵最小的成像时刻便是最优成像时刻,所对应的图像会作为最终自聚焦成像结果并输出。图像熵定义为:
(14)
其中xij为大小为m×n的图像在像素点(i,j)处的像素值。
3 仿真分析
为论证所提自聚焦成像算法的有效性,本节将通过对场景模拟回波数据进行自聚焦成像处理来说明。场景回波数据采用探地雷达正演软件gprMax进行模拟[14],激励信号为中心频率为1.5 GHz的Ricker脉冲。其中地下介质的相对介电常数为6,相对磁导率为1,电导率为0.001 S/m,收发天线以1.6 cm的步进间隔在介质表面移动。
第一个仿真场景为二维半空间模型,如图1所示,位于场景中心的目标为半径3.5 cm金属圆柱体。收发天线紧贴地表,从x=0.2 m处步进移动至x=1.8 m。利用基于波场互相关的成像算法对仿真回波数据进行成像处理,图2为介质相对介电常数εr分别估计为4、6、8、10时的零时刻成像结果。可以看出,在零成像时刻,当εr准确估计为6时,所得图像聚焦效果良好;当εr估计值低于或高于其真实值时,点目标位置会偏离其真实位置,成像结果会出现一定程度散焦,且散焦程度会随εr估计误差的增大而增强。

图1 点目标二维场景模型Fig.1 The two-dimensional model of point target

图2 不同介电常数估计值零成像时刻算法 对点目标的成像结果Fig.2 Imaging results of point target for different estimated relative dielectric constant at focusing time zero
在实际应用中,介质的相对介电常数并不能准确估计,故所提算法在零成像时刻的聚焦图像必然会出现散焦现象。为论证所提自聚焦成像算法性能,估计εr分别为4、6、8、10时(真实εr=6),利用所提自聚焦成像算法对回波数据进行成像处理。聚焦图像熵值随成像时刻变化曲线如图3所示,最优成像时刻t所对应的算法自聚焦成像结果如图4所示。
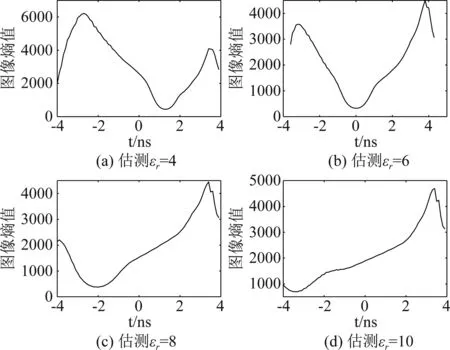
图3 图像熵随成像时刻的变化曲线Fig.3 Image entropy at different focusing time

图4 不同介电常数估计值点目标自聚焦成像结果Fig.4 The autofocusing imaging results of point target for different estimated relative dielectric constant
其中,图3中的时间步进为0.1 ns,从图中可知,利用所提自聚焦成像算法,当介质εr估计值小于真实值时,最优成像时刻滞后于0时刻;当介质εr估计值等于真实值时,最优成像时刻即为0时刻;当介质εr估计值大于真实值时,最优成像时刻提前于0时刻。图4为不同的介质εr估计值,单目标场景回波经所提算法处理后的自聚焦图像。可以发现,尽管介电常数存在误差,所提算法仍能将点目标有效聚焦,验证了所提算法的自聚焦成像性能,但介电常数误差越大,所得图像旁瓣电平有所提升,聚焦效果相对变差。
为进一步论证所提算法的自聚焦成像性能,仿真了V形目标二维场景回波,其数据采集方式与单目标场景相同,如图5所示。图6是不同的介质εr估计值,V形目标仿真回波数据经所提自聚焦成像算法处理后的图像。对比成像结果可知,在介质介电常数存在不同程度估计误差的情况下,所提算法自聚焦处理图像仍能够反映目标的原始几何形状,也进一步验证了所提算法的有效性。但是,随着介电常数误差的增大,V形目标会发生一定程度形变,即张角有所变化,且目标能量的聚焦效果也有所降低。
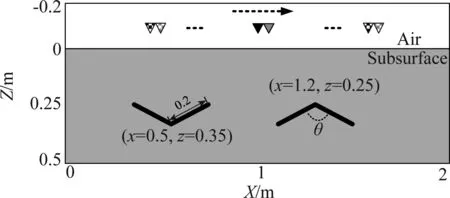
图5 V形目标二维场景模型Fig.5 The two-dimensional model of V-shaped targets
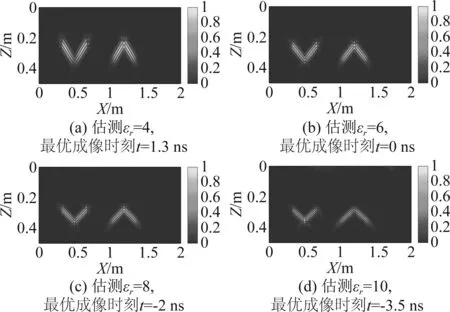
图6 不同介电常数估计值V形目标自聚焦成像结果Fig.6 The autofocusing imaging results of V-shaped targets for different estimated relative dielectric constant
通过引入时间相位因子,所提自聚焦处理算法仅能补偿由介质介电常数估计偏差引起的线性相位误差,而对于探地雷达在空间移动引起的二次相位误差并不能完全补偿。介质介电常数误差越大,相位因子的补偿效果会相应下降,所提自聚焦处理方法的有效性也会随之降低。因此,使用所提算法对探地雷达回波数据进行成像处理时,应尽量保证介质介电常数估计误差在一定合理范围内。
4 结论
提出了一种基于波场互相关的探地雷达快速自聚焦成像算法。相比于传统时域逆时偏移算法,所提算法通过引入水平分层介质频域格林函数,减小了对计算和存储资源的需求,通过快速傅里叶变换大幅提升了算法的计算效率,因此能够快速对地下目标进行高分辨成像。针对介质参数未知而导致的图像散焦问题,通过引入时间相位因子可以得到不同聚焦时刻的图像,然后基于图像熵最小准则得到最优成像时刻及其对应的自聚焦图像。仿真结果表明当介质相对介电常数存在一定估计误差时,所提算法仍能够得到目标的高分辨率自聚焦成像结果。

