强侧风下中速磁浮列车在高架桥上运行时的气动特性研究*

高 锋 罗华军 杨 颖 吴志会 张文跃 周 鹏 侯 磊

(1.中车株洲电力机车有限公司，412001,株洲；2.磁浮交通车辆系统集成湖南省重点实验室，412001,株洲∥第一作者，高级工程师)

与传统轮轨接触式列车相比，磁浮列车具有噪声小、爬坡能力强、曲线半径小、能耗小等优点。近年来，在以“绿色和智能”为主题的城市轨道交通系统中，磁浮列车开始扮演越来越重要的角色[1]。目前，国内外学者对磁浮列车的研究主要集中在无环境风的明线平地工况上[2-3]。而在强侧风作用下，列车空气动力性能恶化，列车运行的横向稳定性会受到影响，严重时将会导致车轨接触或倾覆[4-5]。特别是列车在高架桥上运行时，列车的绕流流场改变更为突出。尽管现阶段对轮轨列车在高架桥、有路堤和路堑等有特殊风环境桥上运行时的空气动力学特性已经开展了大量的研究[6-8]，但是，由于磁浮列车特殊的结构和传动方式，强侧风环境下磁浮列车在高架桥运行时空气动力学性能不能全按照轮轨列车的结论来分析。本文采用数值计算的方法，对中速磁浮列车(以下简称“列车”)在不同风速的作用下以不同速度通过高架桥时的空气动力学特性进行研究，探讨强侧风作用下列车的气动载荷大小和性能。本文的研究结论可为列车的外形设计、车-轨动力学分析、悬浮系统及导向系统稳定性分析提供必要的数据支撑，可为运营方提供制定运行安全措施的参考数据。

1 数值模拟计算

1.1 计算模型

本文采用的列车模型为4节编组，列车总长54.50 m，车宽3.70 m，车高4.40 m。模型为单线高架桥，高为10 m。单线高架桥线路上运行的列车模型如图1所示。

图1 单线高架桥上运行的列车模型

1.2 数学模型

列车速度分别为120 km/h、160 km/h、200 km/h、250 km/h，侧风速度分别为15.0 m/s、20.0 m/s、25.0 m/s、30. 0 m/s、37.3 m/s，对应的风向角在15°到50°之间。列车周围空气流速的马赫数小于0.3，空气可视为不可压缩气体。强侧风环境下，列车在高架线路上运行时的空气流动为湍流流动。目前模拟湍流的数值方法主要有直接数值模拟(DNST)、大涡模拟(LES)、雷诺应力模型、涡粘性模型(k-ε与k-ω模型)等方法。其中标准k-ε两方程模型在列车周围空气流场流动的湍流数值模拟中应用最为广泛[10-11]，且能节省计算资源和时间，因此选用标准k-ε两方程模拟列车周围的湍流流动。

本文采用基于有限体积法的计算软件，选用SIMPLEC算法求解速度和压力的耦合方式，采用基于格林高斯的单元法控制梯度变化，采用二阶迎风格式离散对流相。

1.3 计算区域与边界定义

本次研究采用吹风法(列车静止，空气和地面运动)模拟运行中列车的外部流场。该方法已经普遍应用于国内外对列车明线运行时气动性能的研究[12-14]。计算区域如图2所示。列车头端距离前方空气大域的速度入口为60 m，列车尾端距离后方空气大域的压力出口为300 m；列车迎风侧距离空气大域侧边的速度入口为40 m，列车背风侧距离大域的侧边压力出口为110 m。计算区域的底面和轨道设置为滑移地面，顶部面设置为压力出口。

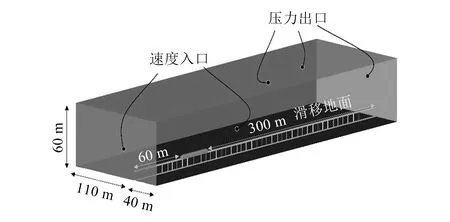
图2 列车模型计算区域与边界条件

1.4 计算网格

为提高网格质量，节约计算资源，本文设定计算域内的网格都为六面体结构化网格。为了更好地模拟列车附近的边界层，通过对车体近壁面区域进行了局部网格加密生成附面层网格。模型第一层网格的厚度为0.125 mm，整个计算区域网格数量为8 570万个。车体表面y+(y表示垂直壁面的方向，+表示无量化)在50左右，满足k-ε两方程模型要求的y+要求范围。列车模型计算网格如图3所示。

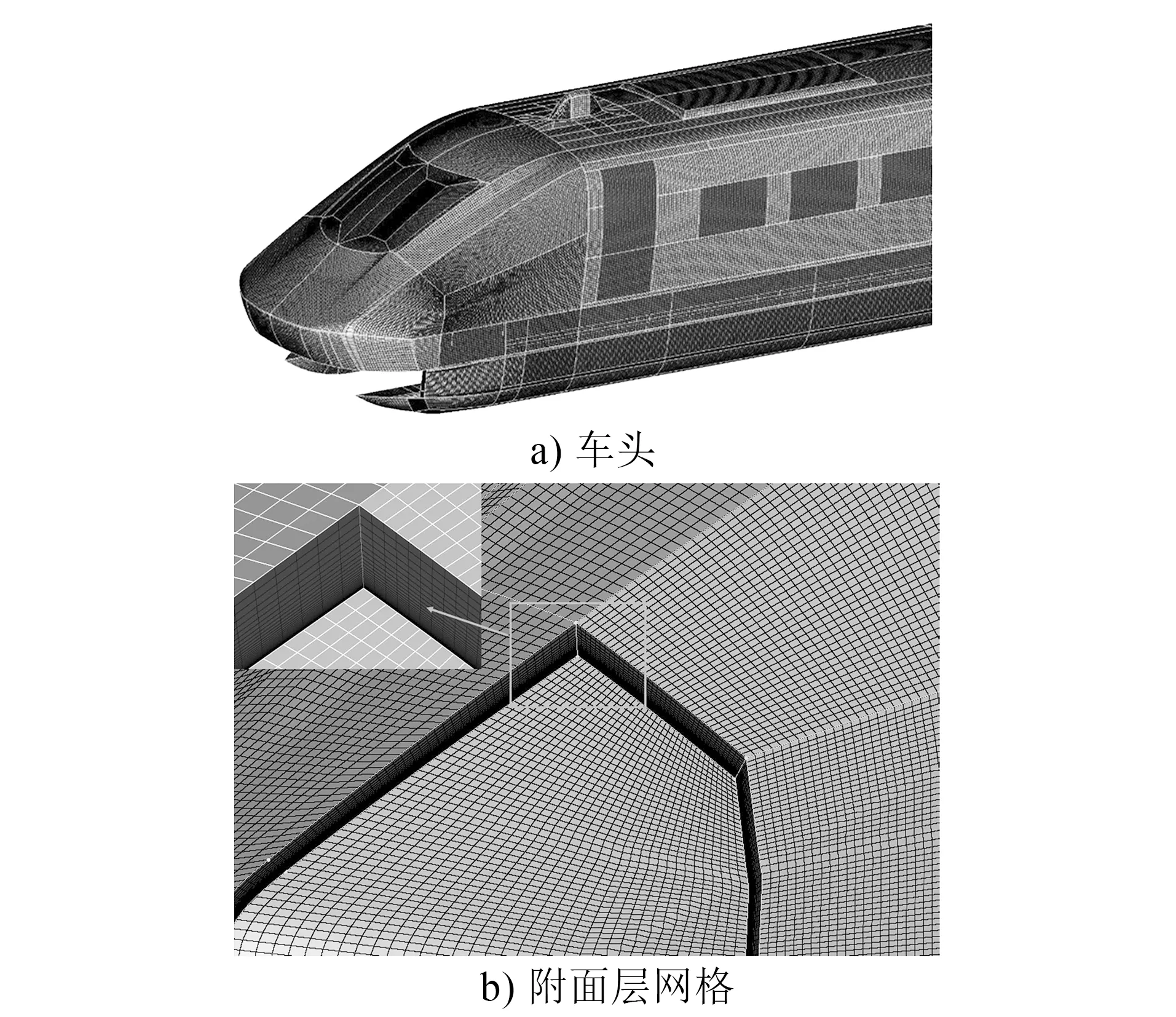
图3 列车模型计算网格

2 数值模拟计算结果分析

2.1 列车气动力分析

为了对比分析列车在不同车速和不同风速下受到的阻力Fx、侧向力Fy和升力Fz，对气动力进行无量纲参数处理，即用阻力系数cx、侧向力系数cy和升力系数cz表示，计算方法为：

(1)

(2)

(3)

式中：

ρ——空气密度；

V——列车运行速度；

S——列车的投影面积。

图4为列车阻力系数在相同车速不同风速和相同风速不同车速作用下的变化情况。列车在10 m单线桥梁上运行时，随着风速的增加，其风向角也增加，当迎风角增大到一定程度时(大约15°)，头车所受的前进方向的力从阻力变成了推力；而中间车1和车2阻力系数随车速和风速的变化基本持平；尾车的阻力系数随着风速的增加而增大，随车速的增加而减少，与风向角成正相关；列车速度为250 km/h、侧风风速为25 m/s时，阻力系数达到极限值。

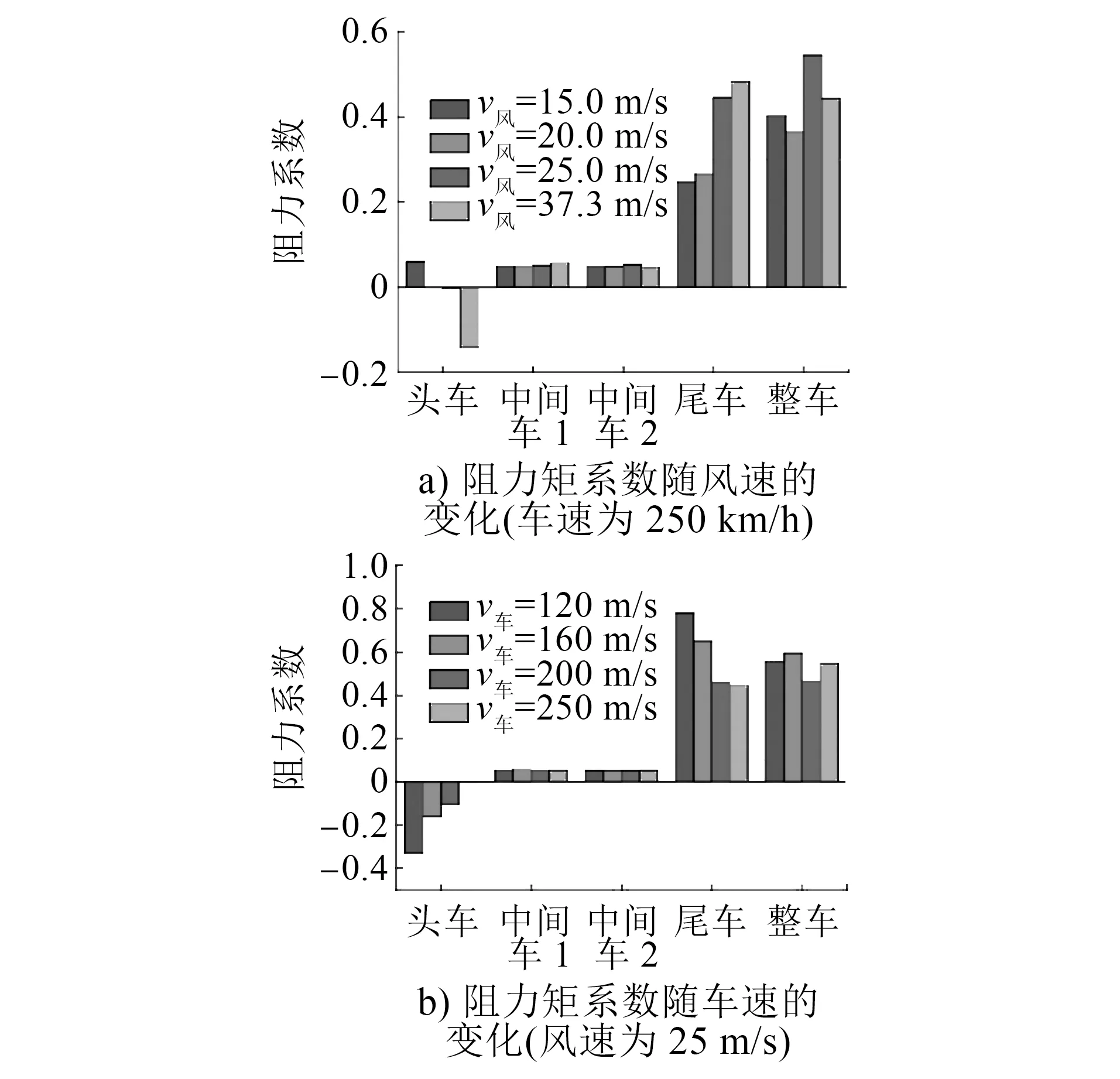
图4 不同车速和风速下的列车阻力系数变化情况

图5为列车侧向力系数在相同车速不同风速和相同风速不同车速作用下的变化情况。列车在10 m单线桥上运行时，整车侧向力系数随着风速的增大而增大，随着车速的增大而减小，与风向角成正相关；当车速为250 km/h、风向角从12.2°增大到28.2°时，侧向力系数增加了320%；在每一种工况下的侧向力中，头车所受的侧向力系数最大，中车次之，尾车最小；当迎风角小于一定角度时(大约19°)，尾车所受的侧向力系数为负值；当列车速度为120 km/h、侧风风速为37.3 m/s时，侧向力达到极限值。

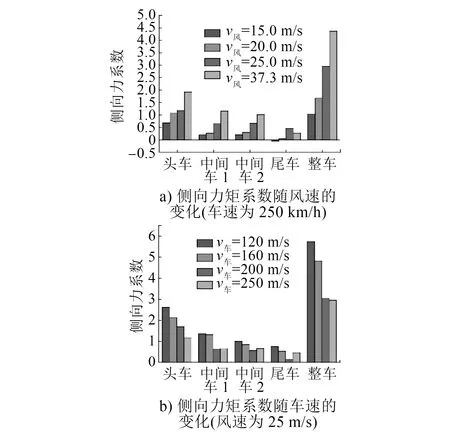
图5 不同车速和风速下的列车侧向力系数变化情况

图6为列车升力系数在相同车速不同风速和相同风速不同车速作用下的变化情况。列车在10 m单线桥梁上运行时，4节车的升力均为正值，但是与车速和风速没有直接的正比关；而整列车的升力系数随着风速的增大而增大，随车速的增加而减小。当列车速度为120 km/h、侧风风速为37.3 m/s时，升力系数达到极限值。

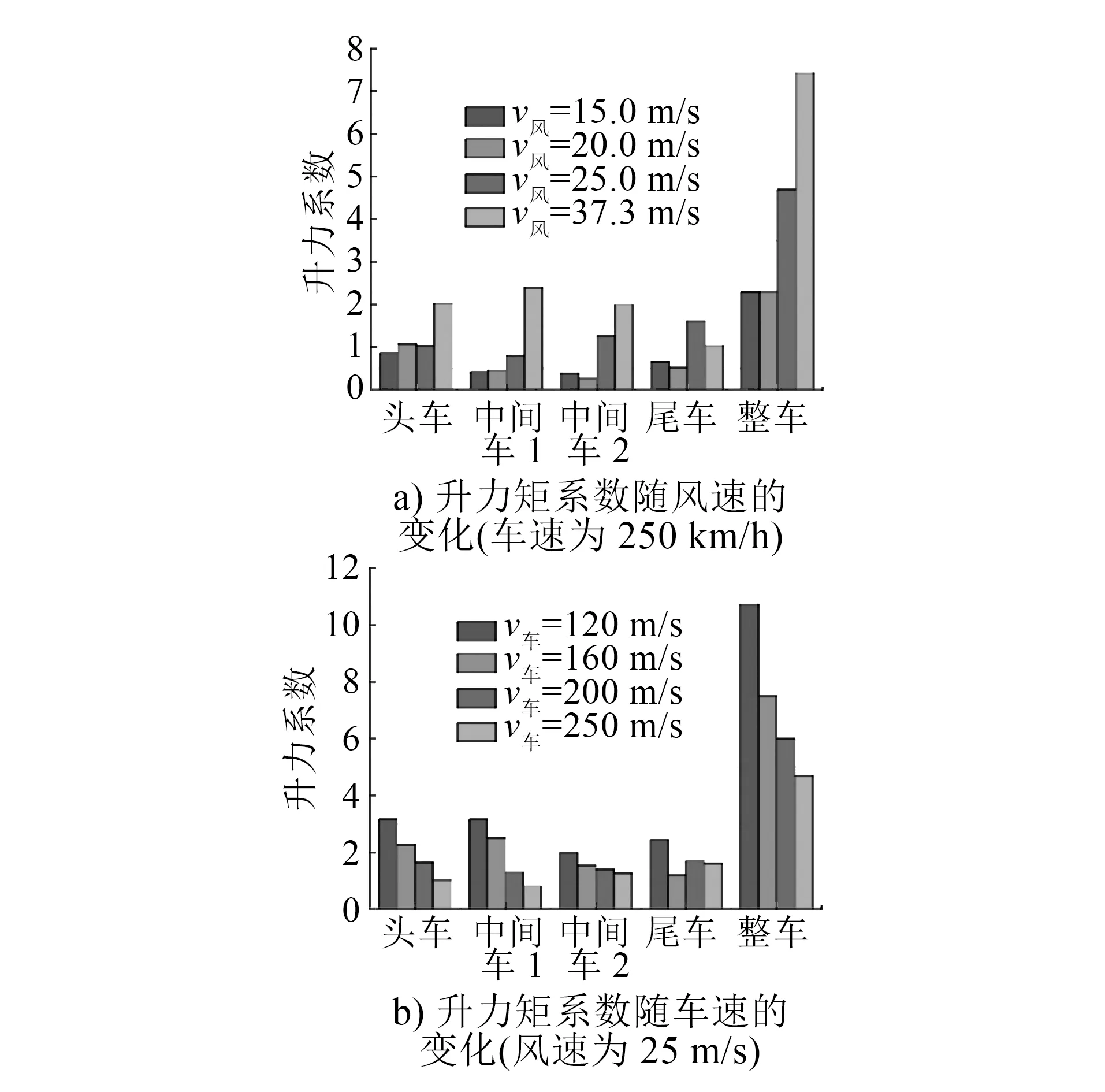
图6 不同车速和风速下的列车升力系数变化情况

2.2 列车气动力矩分析

列车的受到的侧滚力矩Mx、俯仰力矩My、偏航力矩Mz的分析方法与气动力的一致，均采用无量纲参数表示，即用侧滚力矩系数mx、俯仰力矩系数my、偏航力矩系数mz表示，计算方法为：

(4)

(5)

(6)

式中：

l——列车的特征高度，取值为3.34 m。

图7为列车侧滚力矩系数在相同车速不同风速和相同风速不同车速作用下的变化情况。侧滚力矩系数绝对值越大，对于列车运行时的稳定性影响就越大。

列车在10 m单线桥上运行时，整列车侧滚力矩系数、俯仰力矩系数、偏航力矩系数分布呈现相同的规律：随着风速的增大，侧滚力矩系数绝对值增大，如图7 a)所示，37.3 m/s风速作用下的侧滚力矩系数比15 m/s风速作用下的增大了250%；而整列车的侧滚力矩系数绝对值随车速增加而减小，如图7 b)所示，相同风速作用下，250 km/h车速时的侧滚力矩系数比120 km/h车速时的减小了121%；而同一工况下，头车受到的侧滚力矩系数最大，这说明头车最容易发生车轨接触事故；当列车速度为120 km/h、侧风风速为37.3 m/s时，侧滚力矩系数达到极限值。

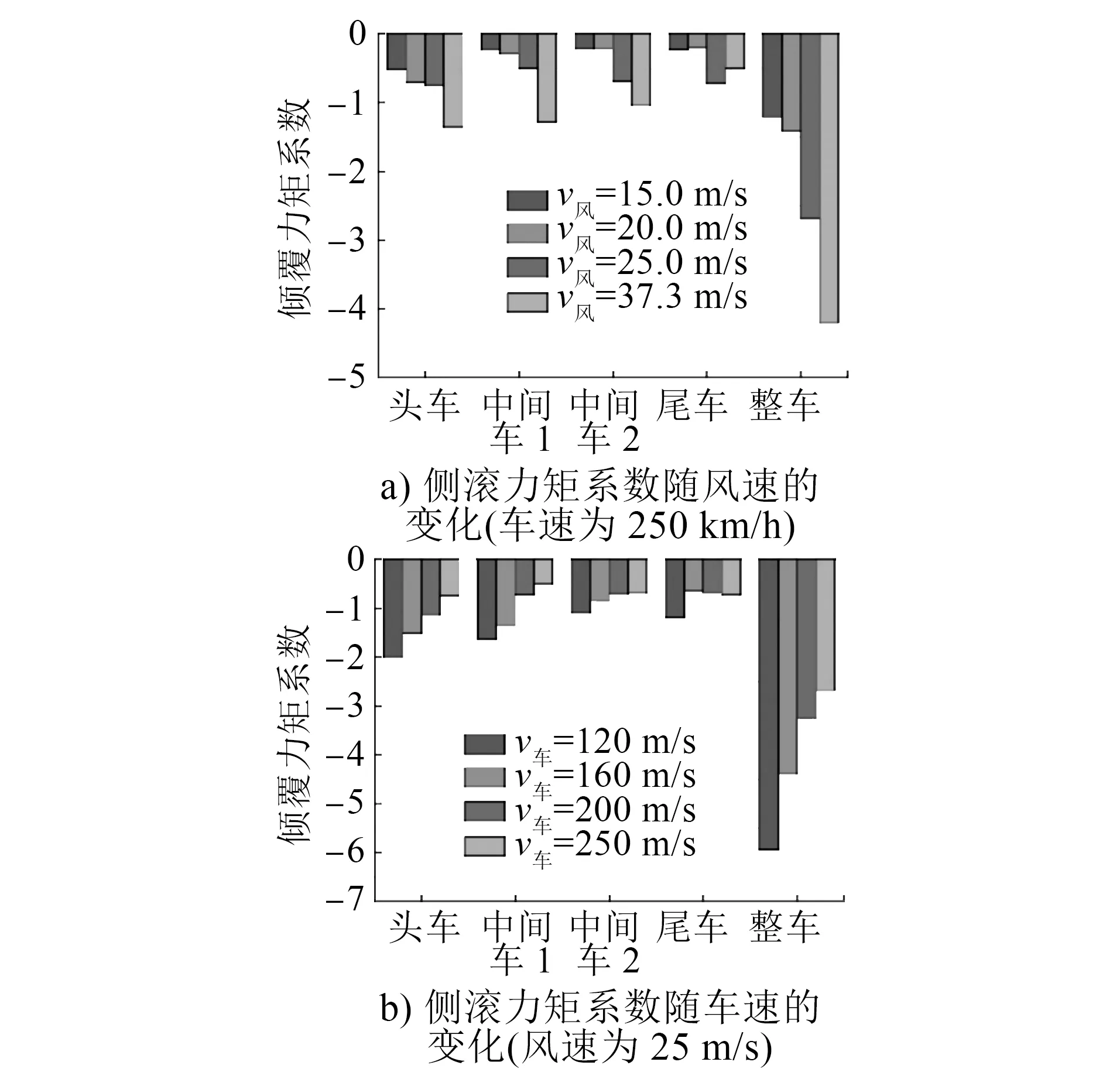
图7 不同车速和风速下的列车侧滚力矩系数变化情况

图8为列车俯仰力矩系数在相同车速不同风速和相同风速不同车速作用下的变化。列车在10 m单线桥梁上运行时，整列车的俯仰力矩系数表现为负值，当迎风角大于一定角度时(大约40°)为正值，这个现象表现在120 km/h车速、30.0 m/s侧风风速(风向角41.9°)和120 km/h车速、37.3 m/s侧风风速(风向角48.2°)的条件下；当列车速度为120 km/h、侧风风速为30.0 m/s时，俯仰力矩系数达到极限值。

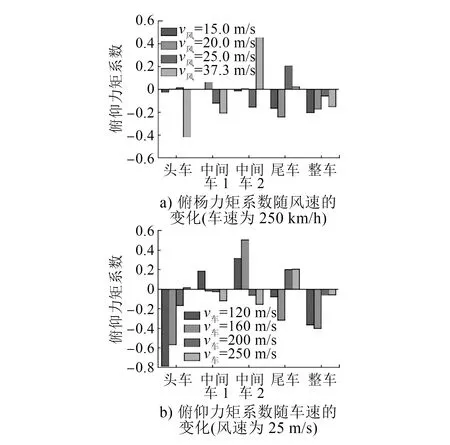
图8 不同车速和风速下的列车俯仰力矩系数变化情况

图9为列车偏航力矩系数在相同车速不同风速和相同风速不同车速作用下的变化情况。列车在10 m单线桥上运行时，整列车的偏航力矩系数的绝对值随风速的增加而增加，随车速的增加而减小；特别是列车的头车和尾车，其偏航力矩系数较大，容易引起车辆的左右晃动；当列车速度为250 km/h、侧风风速为37.3 m/s时，偏航力矩系数达到极限值。

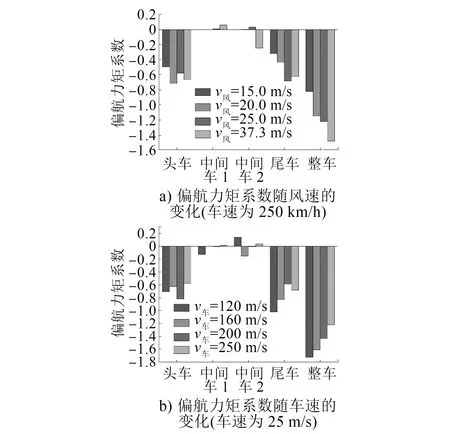
图9 不同车速和风速下的列车偏航力矩系数变化情况

2.3 列车表面压力分布

图10为列车在10 m单线桥上以250 km/h速度运行，侧风风速为15 m/s时，车体不同位置处的表面压力云图。由图10可知：在强侧风下运行时，中间车体迎风侧为正压，背风侧为负压；头车头部迎风侧为比较大的正压，背风侧为较大负压，这也是头车侧向力系数较大的原因；尾车由于受到尾涡的影响，其尾部部分迎风侧的压力也出现负压，使得尾车所受到的侧向力系数比较小；车体顶部由于流体的绕流作用均为负压，而列车抱轨运行和采用主动导向技术，车体底部不受环境风的直接冲击，因此，在环境风的作用下，车体将受到较大的升力作用。

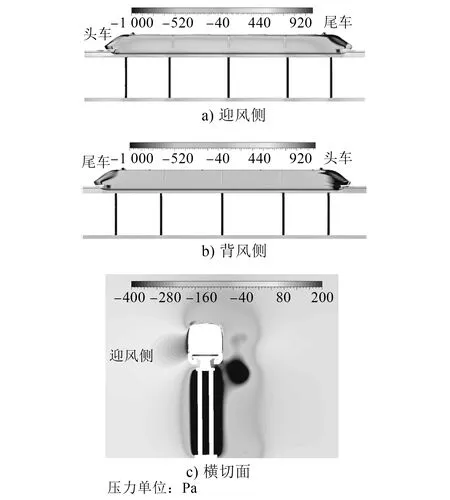
图10 列车运行速度为250 km/h、侧风风速为15 m/s时车体不同位置处的表面压力云图

3 结论

1) 列车整车受到的侧向力、升力、侧滚力矩、偏航力矩随风速增加而增加，随车速增加而减小，与风向角成正相关。

2) 在强侧风下运行时，整车绝大部分迎风侧为正压，背风侧为负压；尾车由于受到尾涡的影响，部分迎风侧的压力也出现负压。

3) 相同工况下，头车受到侧向力和侧滚力矩最大，最容易发生车轨接触故障。

4) 相同工况下，尾车和头车受到的偏航力矩较大，容易引起车辆的左右晃动。