Strain-tuned magnetic properties in(Ga,Fe)Sb:First-principles study∗

Feng-Chun Pan(潘凤春),Xue-Ling Lin(林雪玲),and Xu-Ming Wang(王旭明)

School of Physics and Electronic-Electrical Engineering,Ningxia University,Yinchuan 750021,China

Keywords:GaSb,Fe,ferromagnetism,strain

1.Introduction

In the field of spintronics,dilute magnetic semiconductors(DMSs)that simultaneously provide intrinsic ferromagnetism and semiconducting properties can be achieved by substituting cations in conventional semiconductors with transition metals(TMs)or rare-earth elements,which have attracted much attention in recent decades.[1–5]Among these semiconductors,the III–V GaSb-based DMSs have attracted a large amount of research interest because of their possible high TCvalues and intrinsic ferromagnetism,[6–15]which are critical in applications.Sato et al.theoretically predicted that the TCof Mn-doped GaSb would be proportional to the Mn concentration.[16]Indeed,Tu et al.experimentally confirmed that TCincreased with increasing Fe concentration in GaSb:Fe,and found that TCcan reach 340 K when the Fe amounts to 25%.[12–14]Therefore,increasing the dopant concentration is an effective approach to increase TC.In order to further improve the TM concentration,unconventional preparation methods,such as high pressure and high temperature(HPHT)growth,should be used.[17,18]However,high TM concentrations imply an increasing probability of the second FM phase(such as MnSb),[19,20]which should be eliminated from the viewpoint of applications.Therefore,it is very necessary to seek other effective ways of achieving high TCand inherent ferromagnetism in TM-doped GaSb systems.More recently,many studies have indicated that strain can be used to modulate various physical properties.[21–26]Linpeng et al.highlighted the important contribution of strain to the relaxation and dephasing of acceptor-bound hole spins.[21]Strain can induce a transition from the semiconducting state to a metallic state in some bilayers.[23]It is interesting to note that the magnetocrystalline anisotropy in(Ga0.8,Fe0.2)Sb exhibits a dependence on epitaxial strain and changes its sign from negative to positive when the strain is changed from tensile to compressive.[24]Furthermore,strain is commonly present at heterointerfaces and can easily be controlled by choosing a different substrate.Obviously,it is very significant to investigate the effects of strain on magnetic moment distribution and magnetic interactions in the GaSb:Fe system.

To clarify the influence of strain,in this article we systematically study the electronic structures and magnetic properties of the GaSb:Fe system under different strains using a firstprinciples approach.The results indicate that FeGasubstitution takes place in the LSS with a total magnetic moment of 1µBunder strains in the range of−3%to 0.5%,which transitions to the HSS with a total moment of 5µBas the strain changes from 0.6% to 3%.We attribute the changes to the size and distribution of the total moment to the influence of the crystal field under different strains.We find that the FM coupling is strongest under about 0.5% of tensile strain,which gradually weakens with increasing compressive and tensile strains.Our results highlight the important contribution of strain to magnetic moment and FM interaction intensity,and present an interesting avenue for the future design of high TCmaterials using the(Ga,Fe)Sb system.

2.Computational methods

The calculations are carried out according to spinpolarized density functional theory(DFT)and the localdensity approximation(LDA)method of exchange–correlation parameterization,as implemented in the CASTEP package.[27,28]A cutoff energy of 380 eV is used for the plane-wave basis set,and the convergence criterion for selfconsistent calculation is set to 1.0×10−6eV/atom.Brillouin zone sampling is performed using gamma-centered 3×3×3 Monkhorst–Pack k-points.[29]The ion–electron interaction is described by the ultra-soft pseudopotential(USPP)method.In order to better describe the electronic structures of intrinsic GaSb,the Hubbard U parameter has been employed to treat both Sb-3p and Ga-3d electrons.We tuned a number of the different parameters of U to match the experimentally observed values of the band gap(Eg)and the lattice constants as far as possible,and we finally selected U values of USb-3p=3.0 eV,UGa-3d=2.5 eV.The larger USb-3p mainly stems from the fact that the band edge is dominated by the characteristics of Sb-3p,and is more effective at opening the gap of GaSb,which is similar to that of TiO2.[30]With these parameters,the calculated values of Eg=0.809 eV,a0=b0=c0=5.9116˚A,are in good agreement with the experimental ones.[31]The relaxed structure of blende GaSb is shown in Fig.1.In this article,the strain is defined asε%=(a−a0)/a0,where a0and a are the unstrained and constrained lattice constants,respectively.For each deformed structure,all atoms are fully relaxed,with a fixed lattice constant.

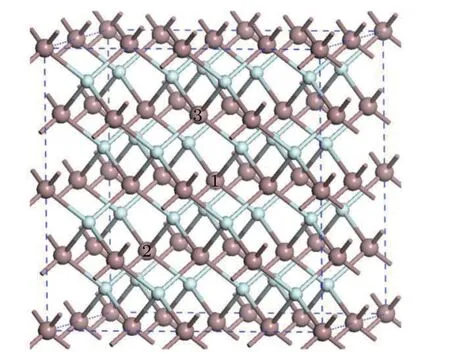
Fig.1.The structure of GaSb;the big and small balls represent Ga and Sb atoms,respectively.Arabic numerals denote the sites of doped Fe.

3.Results and discussion

We first studied the effect of strain on the electronic structures and magnetic moment of a single-FeGa-doped GaSb system.Our results indicate that the Fe is in the LSS and that the density of states(DOS)and the distribution of the magnetic moment are similar to those when the strain in the range of−3% to 0.5%.The total DOS(TDOS)and projected DOSs(PDOSs)at a strain of 0%are presented in Fig.2.As shown in Fig.2(a),the asymmetric electron occupation between the spin-up and spin-down states indicates that there is a magnetic moment in the system.The PDOSs in Figs.2(b)–2(d)further clarify the source of the magnetic moment.For Fe-d electrons,the number of occupied spin-up electrons is more than that of occupied spin-down electrons,which can provide positive magnetic moments.However,for Sb(the nearest(N)and the next nearest(NN)to Fe)-s/p electrons,the number of occupied spin-down electrons is larger than that of occupied spinup electrons.Therefore,the magnetic moments from Fe-d and the surrounding Sb-s/p electrons should be anti-parallel.As shown in Fig.3(a),the distribution of spatial net spin electron density intuitively illustrates that the magnetic moments contributed by Fe-d and the surrounding Sb-s/p are,indeed,antiferromagnetic(AFM).Our results show that the total magnetic moment induced by FeGais always 1µBas the strain changes from−3%to 0.5%.

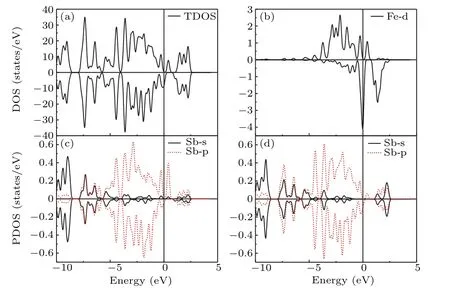
Fig.2.Calculated TDOS(a)and PDOS for(b)Fe-d electrons,(c)Sb(N to Fe)-s/p electrons,and(d)Sb(NN to Fe)-s/p electrons in a single-FeGa-doped GaSb system at a strain of 0%.The vertical lines denote the Fermi level.The TDOS and PDOS under strains of−3%to 0.5%have similar properties.

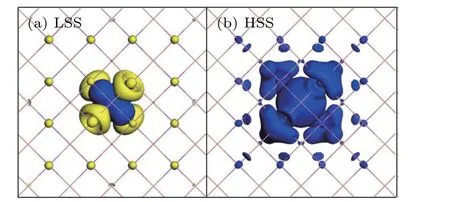
Fig.3.The isosurface of spatial net spin electron density(a)in the one-FeGa-doped GaSb system at a strain of 0%,(b)at a strain of 1%.The blue and yellow parts denote the spin-up and spin-down spatial net spin electron density,respectively.The isovalue is set to 0.01 e/˚A3.

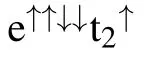
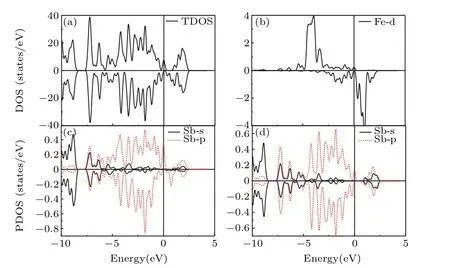
Fig.4.Calculated TDOS(a)and PDOS for(b)Fe-d electrons,(c)Sb(N to Fe)-s/p electrons,and(d)Sb(NN to Fe)-s/p electrons in a single-FeGa-doped GaSb system at a strain of 1%.The vertical lines denote the Fermi level.The TDOS and PDOS under strains of 0.6%to 3%have similar properties.

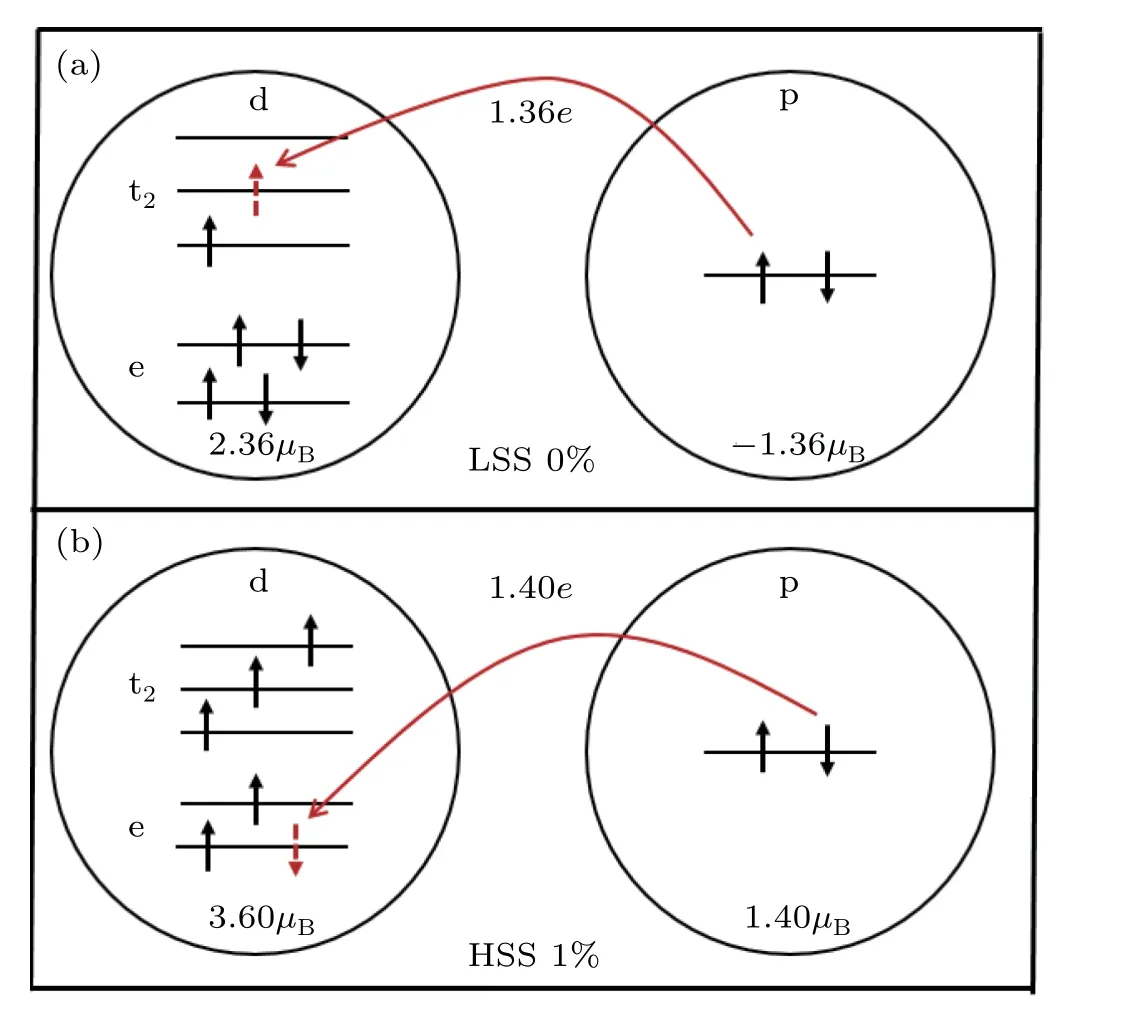
Fig.5.Diagrammatic sketch of the magnetic moment when(a)Fe is in the LSS at a strain of 0%,and when(b)Fe is in the HSS at a strain of 1%.

The results of the study indicate that the total magnetic moment remains constant in the LSS or the HSS,but that the partial magnetic moment changes with strain,as shown in Fig.6.In the range of−3%to 0.5%,the portion contributed by Fe is slightly enlarged and the portion contributed by Sb is slightly reduced with increasing strain.When the strain is 0.6%,the magnetic moment due to Fe sharply increases to 3.59µB,which indicates that the spin state of Fe changes to the HSS.Meanwhile,the portion due to Sb also suddenly increases.It is obvious that the portions due to Fe and Sb are basically unchanged as the strain changes from 0.6%to 3%.

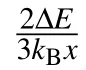
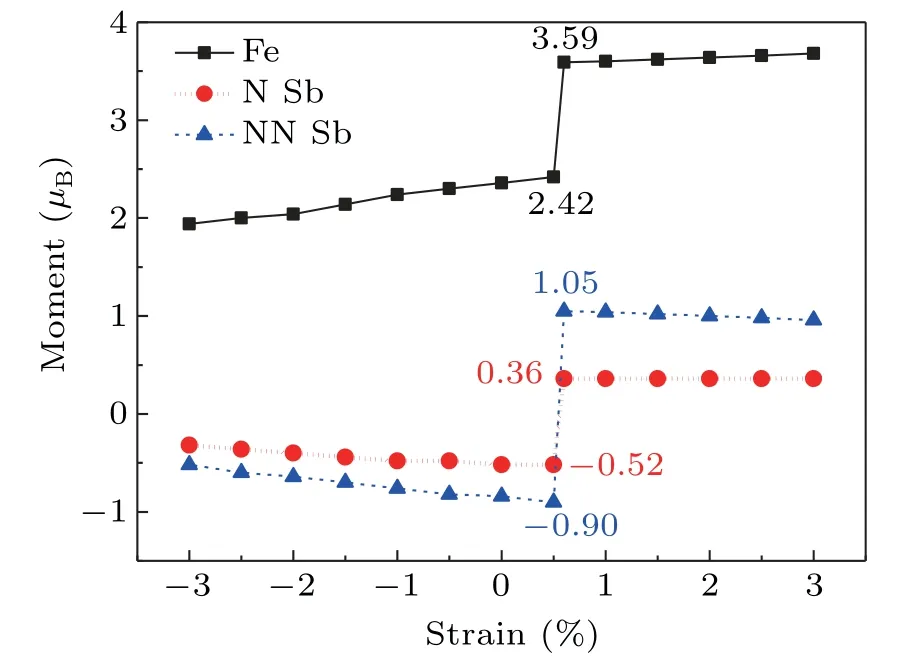
Fig.6.The magnetic moment distribution with varying strain.

As shown in Fig.7,the TCvalues for SI and SII gradually increase with decreasing compressive strains in the range of−3% to 0.5%,and reach maxima of 311.8 K and 202.5 K at a strain of 0.5%,respectively,which decrease sharply as the strain increases to 0.6% and then continue to decrease with increasing strain.The maximum of 311.8 K for SI is close to the value of 336 K in(Ga,Mn)Sb with same doping concentration as estimated by mean-field theory.[11]Moreover,TCdecreases dramatically with an increasing distance between Fe atoms when the strain in the range of−3%to 0.5%,while the decreasing amplitude of TCat strains of 0.6%to 3%is not so obvious.Comparing Figs.6 and 7,it is inevitable that the critical value of the FM coupling strength is consistent with that of the Fe spin state.It is interesting to note that in the range of−3% to 3%,the FM coupling is always preferred.From the point of view of FM coupling intensity,the magnetic interaction is strongest at a strain of 0.5%.

Several different coupling mechanisms are responsible for the magnetic coupling properties in DMSs,which can lead to ferromagnetism or anti-ferromagnetism,and are very important to help us to understand the physical scenarios.We will then shed light on the FM interaction mechanism hidden in the GaSb:Fe system under different strains.For the LSS,as shown in Fig.2,near the Fermi level,the spin-up and spin-down states are both occupied for Fe-d(Fig.2(b)),which are located in the band-gap of GaSb.The characteristics of such PDOS structures are schematically depicted in Fig.8(a).Obviously,under these conditions,Fe-d electrons can directly jump into another Fe-d orbital with the same spin orientation and vice versa,which results in FM coupling,as illustrated in Fig.8(a).The FM coupling induced by the electron exchange of Fe-d–Fe-d is a double exchange mechanism,[33]which can be very strong over a short range.[4]As shown in Fig.7,for the LSS in the range of−3%to 0.5%,the TCof SI are higher than those of SII,which proves that the double-exchange model plays a key role in the FM interaction between two Fe atoms.However,for the HSS,as shown in Fig.4,the larger spinsplitting energy pushes the spin-up states of Fe into a deeper level,which are then mixed with the extended and partially occupied spin-up states of Sb-p,as schematically shown in Fig.8(b).Therefore,Fe-d electrons can couple with other Fe-d electrons through the Sb-p orbital,which can also lead to a FM interaction.The FM coupling between Fe-d electrons through Sb-p takes place via p–d exchange,[34,35]which is relatively weak,but works over a longer range.[4]As shown in Fig.7,for the HSS in the range of 0.6 to 3%,the differences of TCbetween SI and SII are not obvious,which is in agreement with the characteristic of p–d exchange.In fact,there is competition between double exchange and p–d exchange for(Ga,Fe)Sb under different strains,as presented in the(Zn,Mn,Li)Se system reported by Zhu et al.[36]In the range of−3% to 0.5%,the double exchange is dominant,while in the range of 0.6% to 3%,the p–d exchange plays a key role.

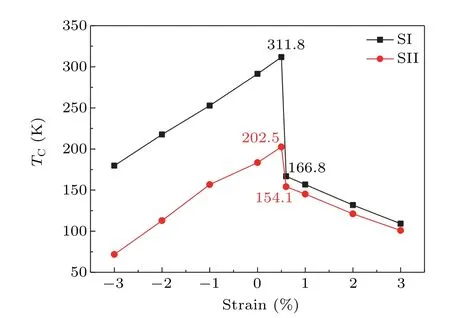
Fig.7.The estimated TC under different strains for SI and SII,respectively.

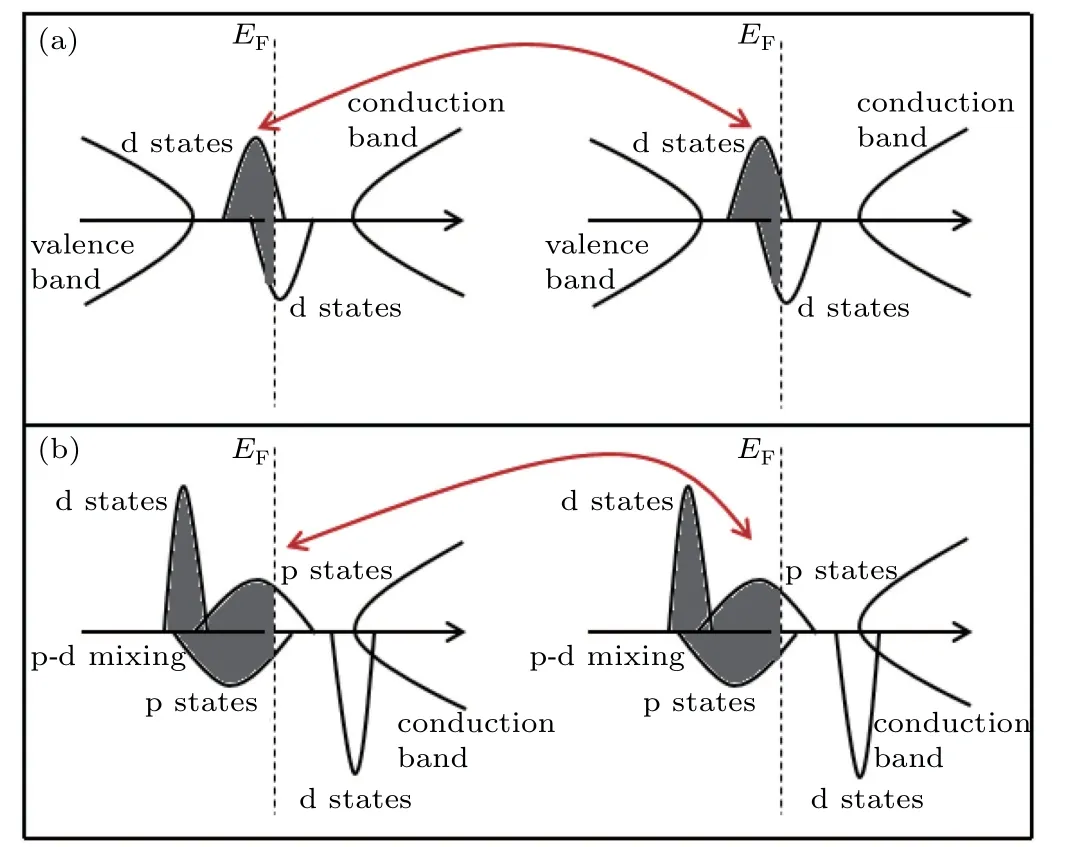
Fig.8.Schematic diagrams of(a)double-exchange for the LSS at a strain of 0%and(b)p–d exchange for HSS at a strain of 1%.Dotted lines and shaded regions denote the Fermi level and occupied states,respectively.

4.Conclusion

The effect of strain on the electronic structures and magnetic properties of(Ga,Fe)Sb have been studied using a firstprinciples calculation.The results of the investigation indicate that FeGasubstitution takes place in the LSS with a total magnetic moment of 1µBunder strains in the range of−3% to 0.5%,which transition to the HSS with a moment of 5µBas the strain changes from 0.6%to 3%.We attribute the changes in the size and distribution of the total moment to the influence of the crystal field under different strains.The FM coupling is strongest at a strain of about 0.5%,and gradually becomes weaker with increasing compressive and tensile strains.The magnetic coupling mechanism can be explained by the double exchange model in the range of−3%to 0.5%,and by p–d exchange model in the range of 0.6%to 3%.Our results highlight the important contribution of strain to magnetic moments and FM interaction intensity,and present an interesting avenue for the future design of high TCmaterials using the(Ga,Fe)Sb system.