基于等效结构应力法的塔吊焊接节点疲劳寿命评估*
刘俊卿,马 岩,曹书文
(西安建筑科技大学 理学院,西安 710055)
随着城市化的进展以及基础建设方面的不断投入,塔式起重机在建筑工地中利用率越来越高,满载、超载现象频频出现,这对起重机的抗疲劳性能提出挑战.对于塔式起重机金属结构的疲劳寿命评估,研究人员做了许多研究[1-2].
焊接作为塔式起重机金属结构中常用的连接方式,因其连接性能好、质量轻、易于加工等特点,被广泛使用,对起重机的力学性能具有重要的影响[3].在具体操作过程中,焊接质量低下、焊接缺陷等问题时有发生,连接部位难免出现应力集中、力学性能不达标等现象,焊接部位的使用周期也会大大缩短,极大地拉低了起重机的力学性能[4].因此,对塔式起重机焊接节点的疲劳强度进行全面细致地分析显得尤为重要.
名义应力法和热点应力法是测试焊接部位疲劳强度的两种常见方法[5-6],然而两种方法都有各自的缺陷和不足:名义应力法在分析时仅针对特定的焊接接头形式与特定的荷载类型,不具备普遍性与通用性;热点应力法则是选取焊接接头附近的焊接点进行外推,利用基于热点应力的S-N曲线数据进行疲劳计算评估,但热点应力法计算结果准确性会因有限元网格的大小、插值点个数以及位置等因素而改变.
基于此,董平沙教授在热点应力法的基础上,结合断裂力学理论拓展了结构应力的概念,创新发明了全新的等效结构应力法[7],对热点应力法进行了优化调整,使得评价结果对单元类型和网格尺寸不再敏感,大大提高了评价结果的准确性和可靠性,该方法已经得到ASME VIII Division2-2010标准的认可[8].本文以QTZ25塔式起重机塔臂下弦杆一焊接节点为对象,利用有限元软件Ansys建立了具有焊缝细节的节点力学模型,使用FE-SAFE/VERITY疲劳分析软件对节点焊缝的疲劳强度进行研究,并对疲劳寿命进行科学地预测分析.
1 基于等效结构应力疲劳评估方法
1.1 网格不敏感结构应力
图1为在外力作用下焊缝截面沿厚度方向的应力分布图,此应力分布因缺口应力而呈现高度非线性.将此非线性应力进行分解,分解后两部分应力如图2所示.图2a为第一部分应力,是只与外力相关且与外力相互平衡的结构应力;图2b为第二部分应力,是去掉第一部分应力留下的缺口应力.虽然缺口应力呈高度非线性,但由于结构应力与外力相平衡,因此,缺口应力的分布一定处于自平衡状态.
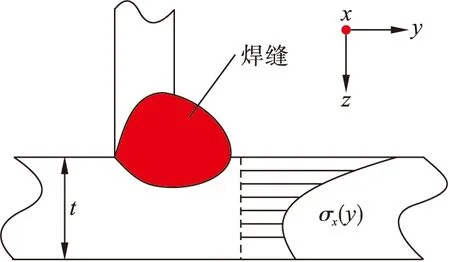
图1 厚度方向应力分布Fig.1 Stress distribution along thickness direction
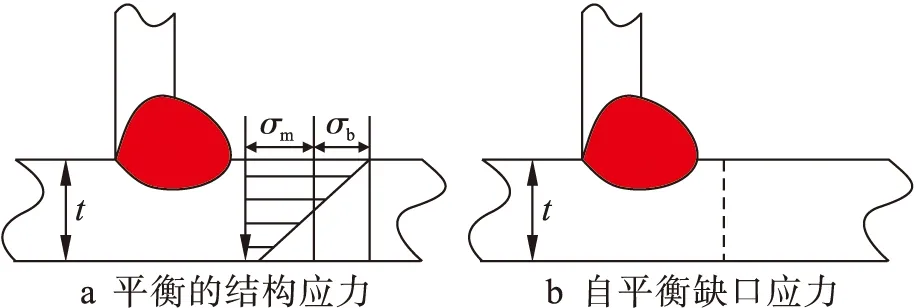
图2 分解后两部分应力Fig.2 Two partial stresses after decomposition
假设当焊接接头所受外力在截面上分为拉伸贡献的膜应力σm与弯曲贡献的拉应力σb,则结构应力中与外力平衡的即是两者之和[9].当给定板厚t时,截面内膜应力计算公式为
(1)
截面内弯曲应力计算公式为
(2)
结构应力σs为膜应力与弯曲应力之和,即
σs=σm+σb
(3)
1.2 基于结构应力的应力强度因子评估
网格不敏感结构应力的确定过程实质上是将复杂结构的三维区域实际应力等效转换为二维简单应力状态[10].图3为三维模型的等效转换,其中,a为边缘裂纹深度,c为焊趾长度.在不断变化的应力作用下,那些拥有裂纹的焊接结构会出现明显的应力集中,最终使得结构体系疲劳强度大大降低,其中,应力强度因子K是评估裂纹开展和断裂的重要参数.通过结构应力计算公式可以建立通用的K估值方法,以便用于所有的焊接接头形式和荷载状态,为后续的等效结构应力推导打下基础.
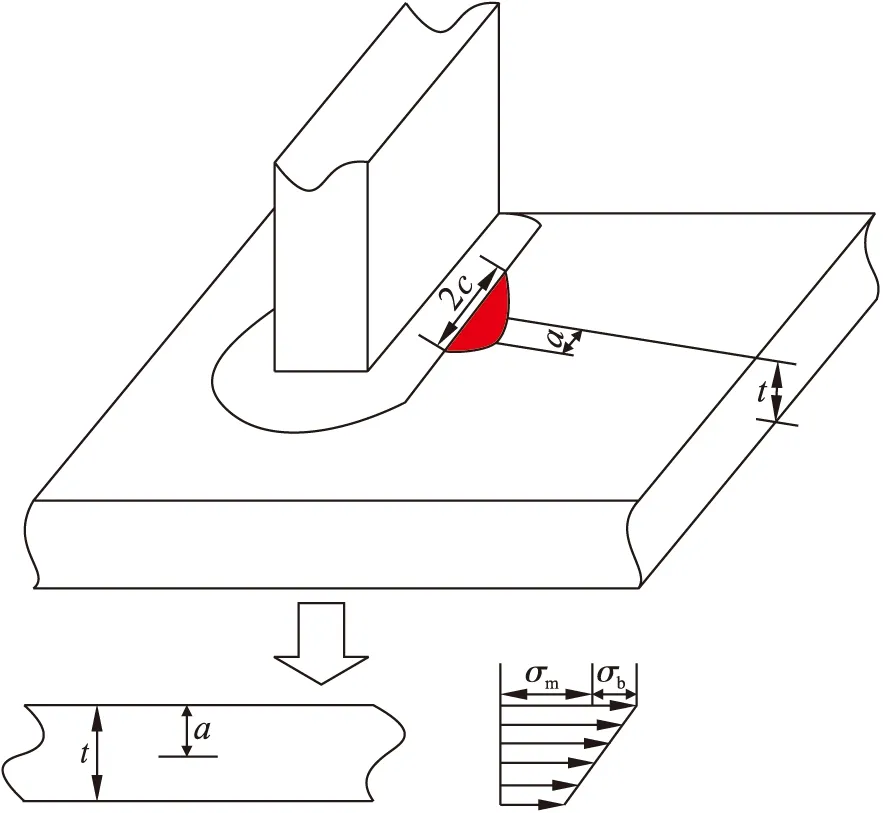
图3 三维模型的等效转换Fig.3 Equivalent transformation of 3D model
在焊接疲劳分析中,无缺口效应的焊趾部位处初始裂纹通常被认为是Ⅰ型裂纹(张开型),焊趾结构失效的重要评价标准就是裂纹穿过焊接部位的厚度.借助叠加原理,焊接部位的所有边缘深度a的裂纹应力强度因子Kn,可以看做是受膜应力时应力强度因子Knm与受弯曲应力时应力强度因子Knb之和,即
(4)
式中,fm与fb分别为膜应力与弯曲应力下的形状参数,是可通过权函数法求得的无量纲参数.
缺口效应指集中应力达到材料的屈服强度时,引起缺口根部附近区域的塑性变形.对于焊缝的任意扩展宽度为a的裂纹,可得缺口效应的应力强度因子[11]为
(5)
式中:Pm和Pb分别为平衡等效缺口应力场的平均正应力与弯曲正应力;fm(a/t)和fb(a/t)分别为平衡等效缺口应力场的膜应力与弯曲应力的形状参数.
当a/t≤0.1时,局部缺口效应显著,Kn(a/t)的求解受远场应力的影响较大;当a/t>0.1时,局部缺口效应不明显,对Kn(a/t)的影响较小,需引入焊趾缺口效应应力强度因子放大系数[12],即
(6)
式中,K(a/t)为远场应力下的应力强度因子.
1.3 裂纹的扩展寿命
在定义疲劳寿命时,金属疲劳被认为是裂纹萌生寿命与裂纹扩展寿命之和,然而当金属通过焊接的方式连接在一起时,疲劳强度会发生本质的变化:疲劳强度将由焊接接头的疲劳强度所控制,而非母材.在焊接结构的疲劳开裂过程中,裂纹萌生对疲劳寿命的贡献可以忽略,因此,焊接结构疲劳强度的核心就是裂纹的扩展寿命[13].本文利用Paris方程可得裂纹扩展寿命的计算公式为
(7)
式中:α为短裂纹(a/t<0.1)扩展指数,其值为2.0;β为长裂纹(0.1≤a/t≤1)扩展指数,其值为3.6;Q为调节系数;ΔKs(a/t)为应力强度因子范围,其表达式为
(8)
Δσs=Δσm+Δσb
(9)
(10)
其中,Δσs为结构应力变化值,Δσm为膜应力变化值,Δσb为弯曲应力变化值,r为荷载弯曲比.将式(8)~(10)代入式(7)可得
(11)
式中,Ir为荷载模式修正系数,是关于荷载弯曲比r的函数,其表达式为
(12)
1.4 等效结构应力转化
当荷载弯曲比确定后,基于等效结构应力范围的疲劳强度曲线Δσs-N也可确定,经推导变换,则有
(13)
因此,等效结构应力[14]可通过焊缝荷载模式修正系数Ir和结构应力变化范围Δσs以及板厚t表示为
(14)
式中,tess为厚度参数,即实际厚度与单位厚度之比,为无量纲参数.
1.5 疲劳设计主S-N曲线
主S-N曲线是对大量焊接接头疲劳强度测试结果进行统计分析得到的疲劳设计曲线,在这些数据被推广之前,通过汽车工业、石化工业以及海上船舶等各种工程领域的试验分析,证明数据是可靠的.在等效结构应力的转化过程中,该曲线合理考虑了荷载模式、焊趾缺口、焊接板厚等影响疲劳寿命的因素,在疲劳设计时,可普遍应用于不同荷载模式、接头类型、母材、板厚等,具有较高的精度与可靠性.
表1为不同概率分布下主S-N曲线试验统计常数.试验统计常数是美国机械工程师协会通过大量试验研究得出,适用于任意走向的焊缝疲劳评估.
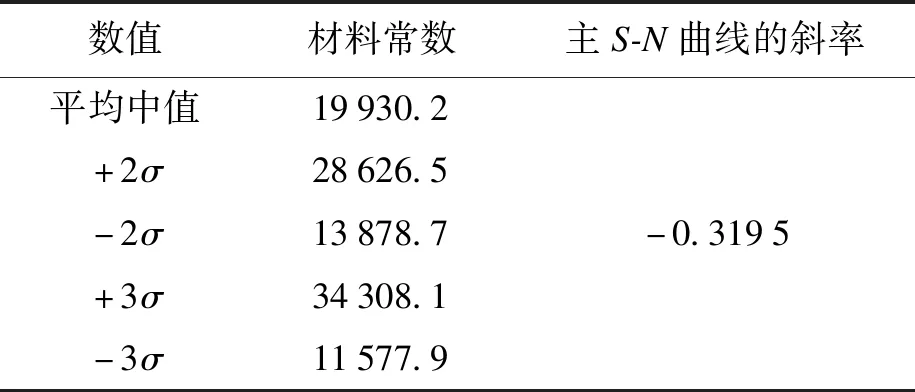
表1 主S-N曲线参数Tab.1 Parameters of main S-N curves
2 工程实例
本文以QTZ25塔式起重机为例,因等效结构应力法在分析评估焊接结构时具有普遍性与适应性,因此,该方法还可用于其他型号塔机的焊接结构疲劳计算与评估.QTZ25塔式起重机金属结构主要由塔身、回转机构、塔帽、起重臂、平衡臂等部分组成.本文选择起重臂中部某下弦外杆与下弦内杆间焊接节点为研究对象,其节点模型如图4所示.其中,下弦外杆为∠180×180×16,下弦内杆为∠65×65×5;下弦外杆与两个下弦内杆间夹角均为45°,内杆与外杆间通过焊接连接在一起,焊接共产生6条焊缝,焊材与母材相同,为Q345钢,弹性模量E为206 kN/mm2,屈服强度fy为345 MPa,泊松比μ为0.5.
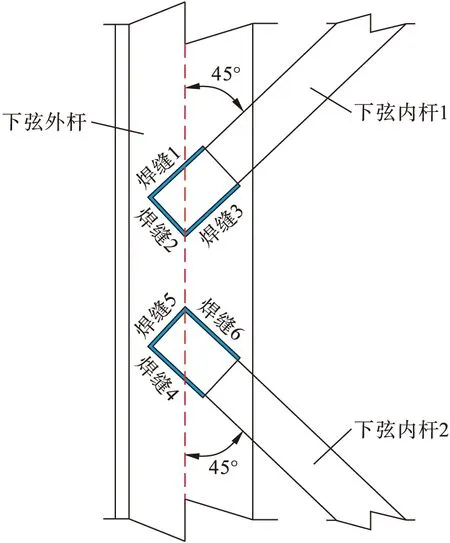
图4 节点模型Fig.4 Joint model
2.1 塔式起重机焊接节点有限元模型的建立
塔吊在工作荷载作用下塔臂的焊接节点发生高周疲劳,进而发生断裂现象.综合分析各个方面的应力变化情况,对塔吊焊接部位的疲劳强度进行全面细致地分析探讨,本文基于大型有限元分析软件Ansys建立包含焊缝细节的有限元模型.焊接节点域(包括焊缝)均采用实体建模,网格划分时单元长度为30 mm,并对焊缝附近网格进行加密处理.
图5为节点应力分布.其中,图5a为焊接节点的整体应力分布图,可知焊接节点的应力峰值为262.9 MPa,与屈服强度相比还有一定的差距,位于下弦内杆2母材和焊缝4的连接部位,这是因为下弦内杆2的焊接部位存在应力集中现象,而应力集中是影响焊接结构疲劳寿命的主要参量,因此,此处是结构疲劳易破坏处.图5b、c为焊接节点焊缝处应力云图,可知6条焊缝应力水平各不相同,其中,焊缝1、3、4、6应力水平较高,为28.6~259.8 MPa,焊缝2、5应力水平较低,为0.2~29.0 MPa.总体而言,节点能够满足静力分析的强度条件.
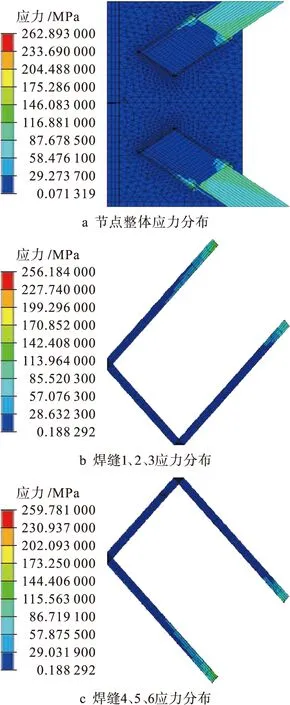
图5 节点应力分布Fig.5 Stress distribution at joints
2.2 基于FE-SAFE等效结构应力的求解及疲劳寿命评估
等效结构应力法是将焊接节点处的节点载荷变成单元边上的分布线载荷,最终计算出焊缝焊趾处不同节点的等效结构应力.综合使用S-N曲线和等效结构应力法能够对焊接部位的疲劳强度进行全面细致地分析评估.FE-SAFE是一款针对疲劳寿命分析开发的软件,其中VERITY模块是借助等效结构应力法而设计开发的专门分析焊接部位疲劳强度的模块,能代替用户完成冗长而又复杂的计算[15].
在进行等效结构应力计算前,需要进行焊趾线(weld toe lines,WTLs)的定义,本文通过整合焊缝单元集的方法,手动定义焊缝1~6总计12条焊趾线,示意图如图6所示.
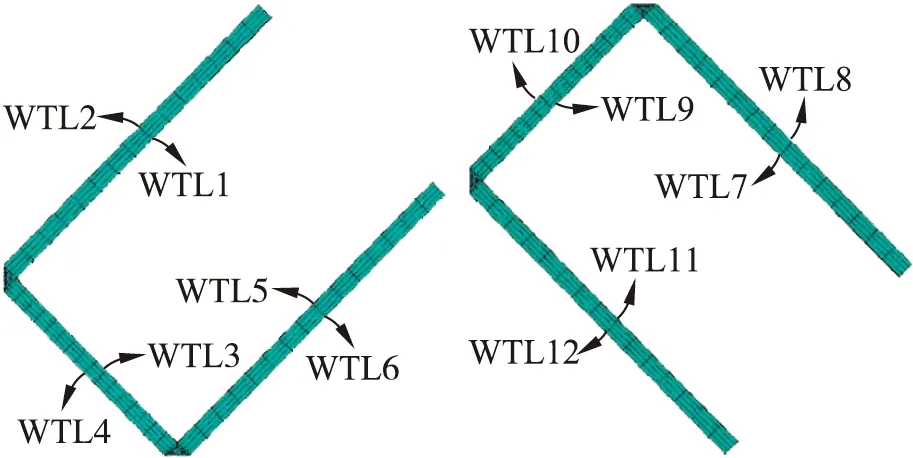
图6 焊缝焊趾线位置Fig.6 Positions of WTLs at weld seam
定义完焊趾线之后,取起点沿焊趾线距离为横坐标,以等效结构应力为纵坐标,计算出按照焊缝长度排列的等效结构应力,如图7所示.由图7h可知,等效结构应力绝对值最大处发生在WTL8中,其值为-513.84 MPa.
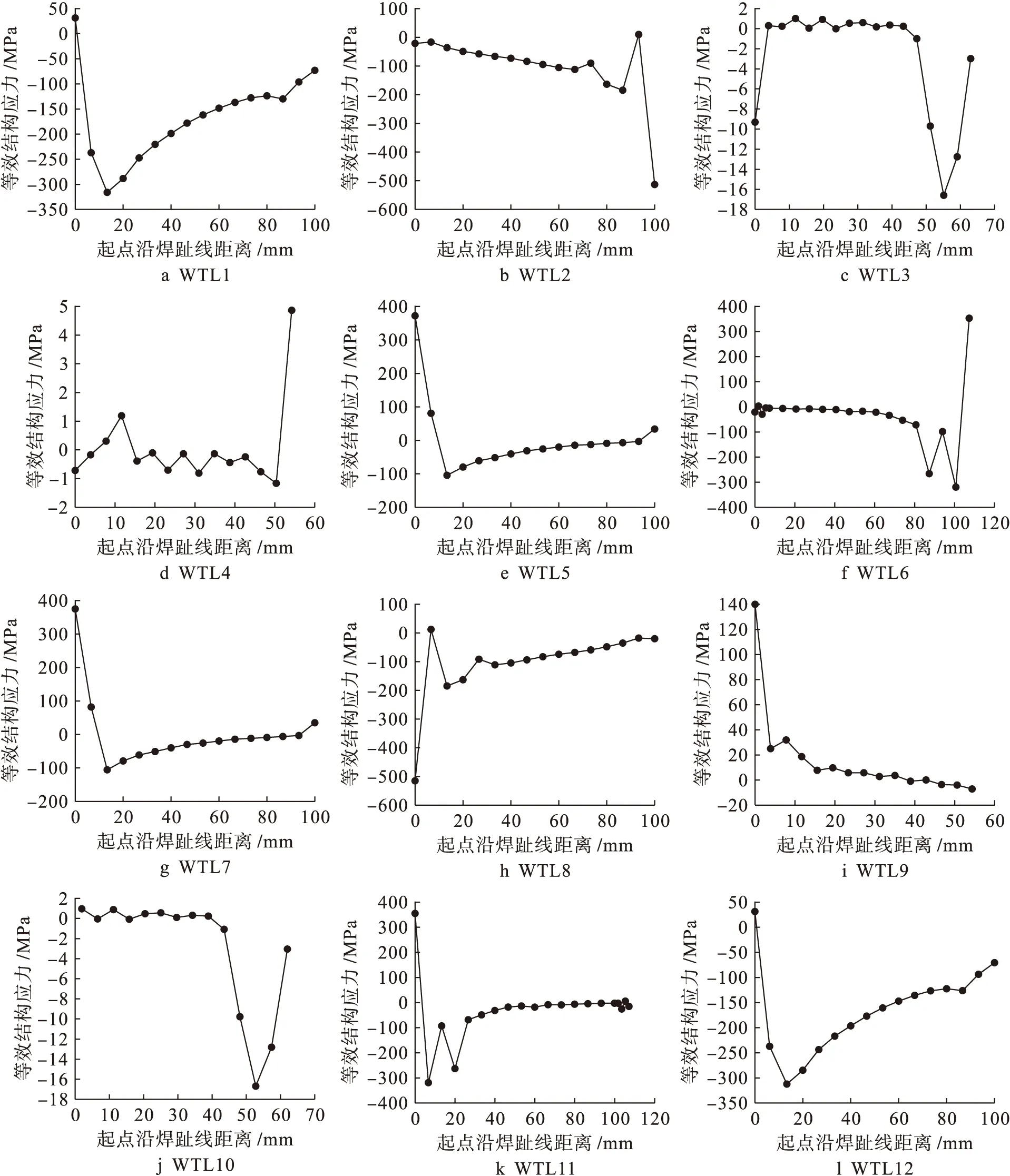
图7 焊接节点焊缝焊趾线等效结构应力Fig.7 Equivalent structural stress of weld toe line at weld seam of welded joints
等效结构应力计算完以后,利用FE-SAFE进行疲劳分析,定义等幅对称交变荷载谱,结合主S-N曲线,得到的疲劳寿命云图如图8所示.由于本文疲劳评估对象是节点焊缝,因此,在寿命云图中只显示了节点焊缝的疲劳寿命.由图8可知,焊缝处最小疲劳寿命为104.945 9,发生在焊缝6的WTL8处,属于高周疲劳,疲劳易破坏位置与应力集中处相吻合.总体而言,该节点焊缝处疲劳寿命可满足工程需求.
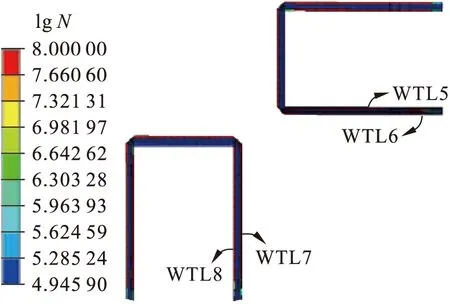
图8 疲劳寿命云图Fig.8 Fatigue life nephogram
2.3 焊缝处疲劳破坏模式分析
图9为两种疲劳失效形式.焊接接头的破坏模式[11]可归纳为两种:破坏模式A是焊缝WTL8处附近沿下弦内杆宽度方向的破坏,是侵入母材的焊趾失效;破坏模式B是裂纹穿过焊缝金属后,沿着焊趾线方向开裂破坏,属于焊缝失效,两种疲劳失效模式均有可能发生.结合图5、7可知,由于WTL8处前端是结构的易疲劳破坏点,而破坏点与下弦内杆交接处母材处于高应力水平,其主应力方向为焊趾线法向,同时沿着WTL8处后段部分的等效结构应力水平相对较低,不易沿焊趾线穿透焊缝破坏.因此,本文中焊接接头所发生的疲劳破坏模式为模式A,即侵入下弦内杆母材的焊趾失效,当WTL8前端发生疲劳破坏时,裂纹会侵入母材,在母材中失稳扩展,最终裂纹穿透母材,构件宣告破坏.
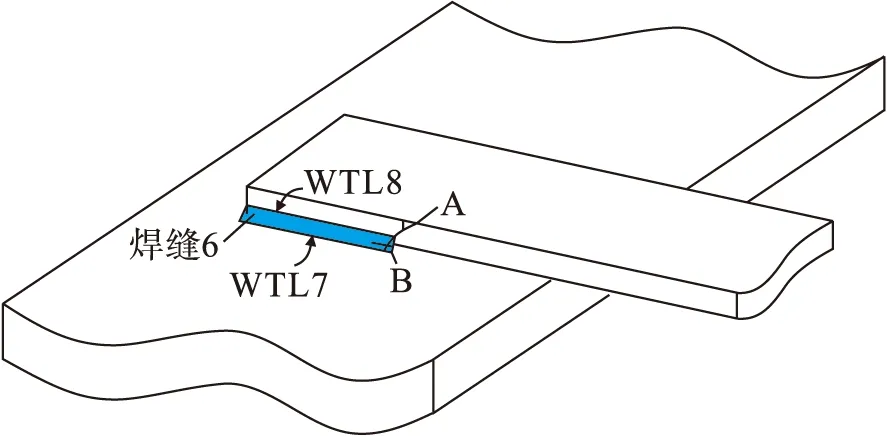
图9 两种疲劳失效形式Fig.9 Two fatigue failure modes
2.4 网格不敏感性验证
为了进一步探讨等效结构应力对网格的不敏感性,本文使用多尺度网格划分进行验证分析,对比WTL8处等效结构应力的结果差异.在Ansys中选择四面体Shell单元,沿着焊缝分别以单元长度为10、20、30 mm进行单元划分,经计算得到3种不同单元尺寸划分下WTL8处等效结构应力,如图10所示.3种不同单元尺寸的等效结构应力最大值分布位置均相同,相同位置处应力值相近且变化规律大致相同.其中10 mm单元尺寸与30 mm单元尺寸焊缝对应的等效结构应力最大差值约为29 MPa,与最大等效结构应力比值为5.65%,证明了等效结构应力法在研究焊缝疲劳时对网格的不敏感性.
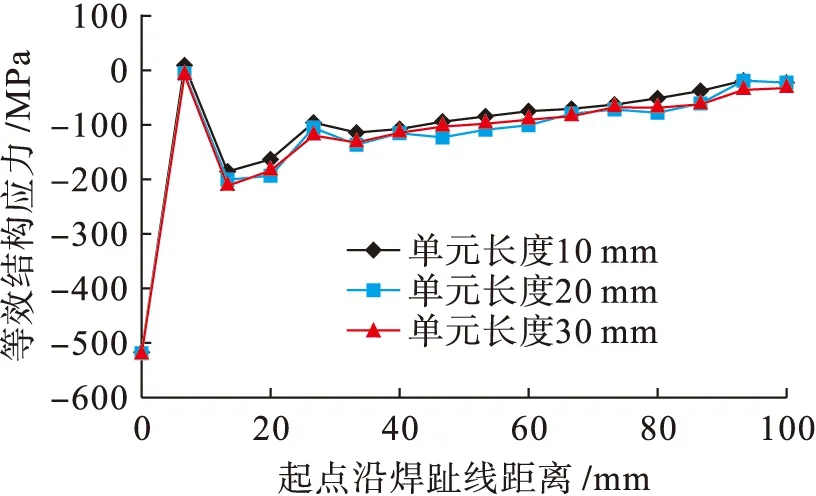
图10 不同单元长度的等效结构应力Fig.10 Equivalent structural stress of different element lengths
3 结 论
通过建立包含焊缝细节的塔式起重机焊接节点模型,运用等效结构应力法结合主S-N曲线分析其疲劳寿命,得到以下结论:
1)等效结构应力法可以同时考虑应力集中、荷载模式等对疲劳寿命的影响,利用等效结构应力法能够较好地预测塔式起重机焊接节点焊缝的疲劳寿命,可为起重机焊接节点结构设计提供参考,还可以用于其他焊接结构处的焊缝疲劳寿命分析评估.
2)对QTZ25起重机起重臂中部某下弦外杆与下弦内杆间焊接节点进行疲劳寿命评估,结构所能承受最大工作循环次数为104.945 9,满足工程需求.
3)该焊接接头疲劳破坏模式为模式A,即裂纹侵入下弦内杆母材的焊趾失效,在母材中失稳扩展,最终裂纹穿透母材,构件宣告破坏.
4)通过对不同单元长度的等效结构应力进行分析,验证了等效结构应力法的网格不敏感性,体现了在分析焊缝结构时,该方法具有一定的优越性.

