基于支持向量数据描述的MEWMA控制图研究

贾蓓蓓

（燕山大学 理学院，河北 秦皇岛 066004）

一、研究背景与意义

随着科学技术的进步，劳动生产力日益提升，商品市场处于供求平衡或是需求较小的市场饱和状态，质量成为赢得市场的关键因素。质量管理贯穿产品生产的整个环节，从设计、生产到销售，每一个环节的产品质量管理都不可或缺，对产品生产的全过程进行监控管理就显得尤为重要[1]。统计过程控制（Statistical Process Control，SPC）便是用来监控这些波动，保证波动处于稳定状态或是在可以控制的范围内的一种方法[2]。

控制图是SPC技术进行产品质量监控的主要工具。20世纪40年代，Hotelling提出了控制图，用于解决多元统计过程问题。该控制图通过当前观测点，对多变量进行监控，由于仅利用了当前信息，历史数据价值损失巨大，对波动较小的过程监控极为困难。针对此缺陷，多元累积和控制图（MCUSUM）与多元指数加权移动平均控制图（MEWMA）应运而生[3]。这些控制图以监控数据服从多元独立正态分布为基本假设，但是在生产过程实际应用中，通常无法判定数据所服从的分布类型，并且很难做到变量间相互独立，使得控制图监控不准确，造成一定的局限性。

随着大数据时代的到来，数据挖掘、机器学习技术飞速发展，机器学习算法被更多人接受并应用于各大领域[4]。因此，开始将机器学习的方法与控制图理论相结合，用来解决控制图由于统计原理不完善、数据分布不确定、参数多元带来的限制问题[5]。支持向量数据描述（SVDD）是基于统计学理论的新兴机器学习方法，适用于高维度、小样本、对样本分布要求不高的数据，刚好弥补了控制图缺陷，应用价值极高。因此，将SVDD模型引进MEWMA控制图，具有极高的研究价值。

二、MEWMA控制图与支持向量数据描述算法相关理论

（一）MEWMA 控制图

MEWMA控制图不仅利用了当前信息与历史信息，而且将时间序列应用于控制图模型中，对统计过程中的小偏移波动反应敏感，具有良好的监控性能。

假设观测值 X=[x1，x2，x3，…，xp]′服从均值向量为u0，协方差矩阵为∑的p元正态分布N（u0，∑）。定义一个统计量：

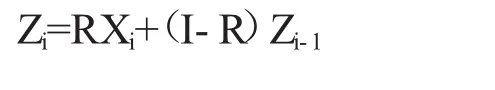
其中，Zi为第i个样本观测值与之前i-1个样本观测值的加权值，Zi的初始值为Z0。R代表各质量特征值的权重，R=diag（r1，r2，…，rp），0≤rj≤1，j=1，2，…，p。I为p阶单位矩阵。根据统计量Zi，MEWMA控制图的统计量为：

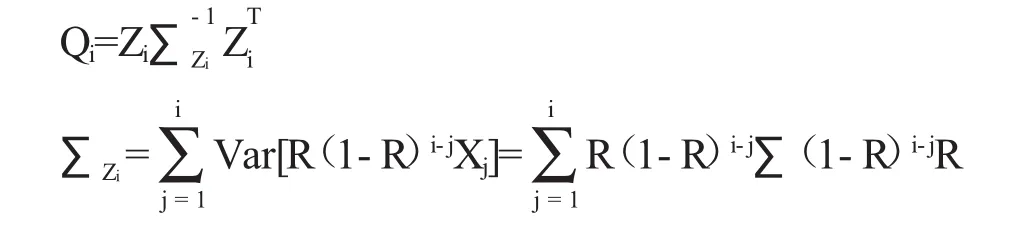
其中，∑Zi是统计量Zi的协方差矩阵，如果权重相同，协方差矩阵可简化为：

对于MEWMA控制图的控制限，通常通过平均运行链长（ARL）计算获得，当权重系数取不同的值，控制限的取值也不同。当控制图统计量超过控制限范围，控制图报警。

（二）支持向量数据描述理论

支持向量数据描述（SVDD）理论是通过将特定的训练集映射到高维空间获得超球体，并使超球体尽可能多的将同类数据包含其中，将不同类数据排除在外的分类方法[6]。因此，该方法也避免了无法获取异常样本的问题，减少了过拟合。

比如，有N个训练集，给定训练集T={xi∈Rd，i=1，…，N}，其中xi是一个d维向量。支持向量数据描述的目的就是企图用一个球心为α，半径为R，R＞0的超球体尽可能多地将目标数据集包含其中。若要满足球体最小，可以通过最小化获得最优解，公式表示为：

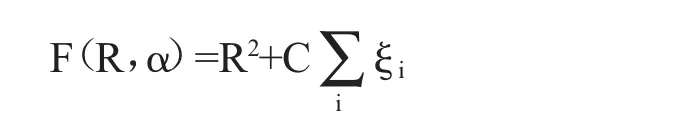
其中，ξi代表松弛变量，C为惩罚因子。

在最小化问题中，所有的目标数据需要包含在超球体中，即每个目标数据到超球体球心的距离小于超球体半径，条件公式表示为：

对于以上求解最优化，一般引进拉格朗日乘子进行计算，有公式：

αi，γi≥0为拉格朗日因子。拉格朗日函数对各参数求导，使求导结果为0。

图1 支持向量数据描述的数据描述过程

将以上求解结果带入拉格朗日方程并转化为对偶问题，有：

针对以上对偶问题进行求解，假设α*为最优解集，α*不为0时对应点Xi的就为分类器边界的支持向量。设R2为超球体半径，定义为支持向量到球心的距离，公式为：

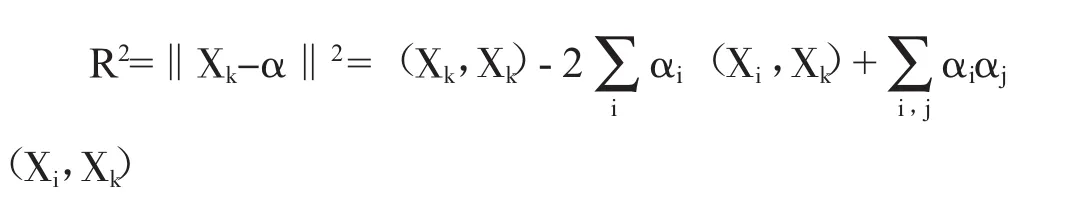
当存在一个点c，判断c点是否数据目标集，就看c点到超球体球心的距离是否在半径内，如果在就属于目标集，不在便可归类于异常数据。点c到球心的距离表示为：

当数据点到球心的距离小于等于半径时，认为该数据点属于目标集，否则认为是异常点。

实际操作中，数据并非如此理想化，有些数据并不是线性可分的，为了提高支持向量数据描述的泛化能力，提高灵活性，引入核函数这一概念。当原始数据集不线性可分时，那么通过核函数将线性不可分的数据集映射到高维空间，转化为高维空间线性可分的问题。研究证明，函数只要满足Mercer定理，该函数便可作为核函数。用核函数代替内积，问题转变为：

相应的，超球体半径和数据c到球心的距离分别转变为：

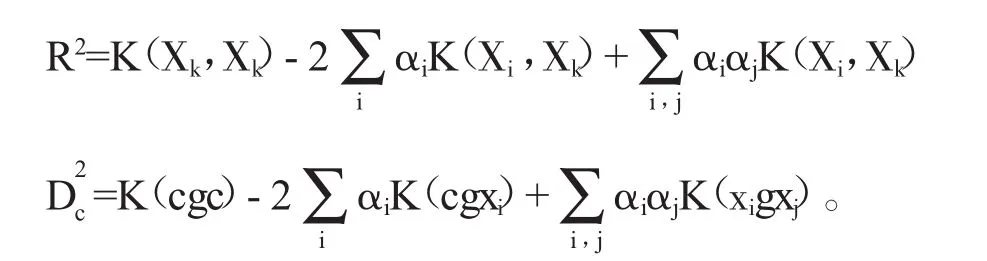
三、基于支持向量数据描述的MEWMA控制图模型设计

产品生产过程受控状态下，有一组观测值为Y（y1，y2，…，ym），作为训练数据，用支持向量数据描述算法对训练样本进行学习，得到一个球心为a，半径为R2的超球体。一组新的观察值 X（x1，x2，…，xn），数据到超球体球心距离为，基于支持向量数据描述的MEWMA控制图设计如下：

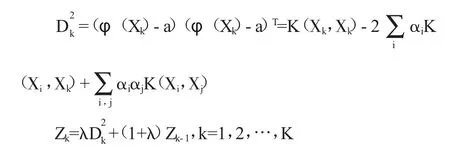
其中，Xk为第k个观测值，初始值为Z0，权重为λ，0≤λ≤1。控制限为h，当产品生产过程受控时，平均运行链长（ARL）决定了控制限h的值。当基于支持向量数据描述的MEWMA控制图统计量Zk＞h时，控制图报警。

四、S-MEWMA控制图与MEWMA控制图对比分析与研究

本文将通过仿真实验，将S-MEWMA控制图MEWMA控制图进行对比，验证S-MEWMA控制图在多元非独立情况下的性能。利用平均运行链长作为控制图的评价标准，当控制图在控平均运行链长ARL0一定时，监控过程发生不同程度的偏移，对比失控平均运行链长ARL1，具有较小ARL1的控制图性能较好。

（一）维度方面

表1 S-MEWMA控制图与MEWMA控制图控制限h

S-MEWMA控制图与MEWMA控制图在不同偏移量下的ARL1结果见表2：

表2 S-MEWMA控制图与MEWMA控制图ARL1

通过万次仿真实验得出的实验结果可知，当φ＜2时，S-MEWMA控制图三维正态分布下的ARL1要低于二维正态分布的ARL1；当φ＞2.5时，三维S-MEWMA控制图与二维S-MEWMA性能基本相同。说明发生偏移越小时，支持向量数据描述对更高维控制图的作用越明显，优越性越显著；当偏移程度增大时，支持向量数据描述对更高维控制图优势减弱。但是对于MEWMA控制图，二维控制图ARL1稍微低于三维控制图ARL1，性能相差不大。无论是二维或是三维，相同维度下，S-MEWMA控制图ARL1明显低于MEWMA控制图ARL1，S-MEWMA控制图性能优于MEWMA控制图，也验证了支持向量数据描述算法比控制图的优势大。

（二）相关性方面

基于二维正态分布，通过构造不同的相关系数，验证基于支持向量数据描述算法的MEWMA控制图的性能。二维正态分布中，S-MEWMA控制图与MEWMA控制图的ARL0仍然设为200，参数f、s值仍然为0.025、1.5，控制图控制限h，失控状态下平均运行链长ARL1同上节。

表3 S-MEWMA与MEWMA控制图的控制限

S-MEWMA控制图与MEWMA控制图在不同偏移量、不同、不同的结果见表4：

表4 二维正态分布下不同相关系数ARL1值

实验结果表明，对于S-MEWMA控制图，变量间相关系数的变化并不会对ARL1产生较大的影响，但是对MEWMA控制图来讲，当变量间相关系数逐渐增大时，控制图性能不稳定性增加，因此，当数据变量间非独立时，S-MEWMA控制图表现出了更好的性能。

五、结论

本文通过仿真模拟方法，将S-MEWMA控制图和MEWMA控制图进行对比，探究S-MEWMA控制图在服从非独立二维正态分布及三维正态分布的情况下的性能。利用平均运行链长作为控制图的评价标准，当控制图在控平均运行链长一定时，监控过程发生不同程度的偏移，对比失控平均运行链长，具有较小链长的控制图性能较好。实验结果表明，S-MEWMA控制图在数据服从非独立二维正态分布及三维正态分布的情况下，相较MEWMA控制图具有更好的性能。