基于数据重构与孤立森林法的大坝自动化监测数据异常检测方法
赵新华,范振东,何 宇,查益华
(1.国网新源水电有限公司新安江水力发电厂,杭州311608;2.中国电建集团华东勘测设计研究院有限公司,杭州311122)
0 引言
大坝监测数据是评估运行期大坝安全性态最直观、最可靠的方法之一[1,3],而自动化监测因其具有快速、实时、在线监测的优势在各大水电站大坝监测中得到广泛应用,但是自动化监测由于采集频次高且容易受雷击、电压等影响,容易出现异常值和毛刺点[4]。若异常值量值与正常值相差较大,则往往会覆盖监测效应量的变化规律。此外自动化监测数据中异常值出现的位置、量值具有不确定性,人工删除异常值存在工作量大、主观性强等不足。目前,常用的大坝监测数据异常值识别方法有逻辑判别法、统计判别法以及基于模型的方法[5,7]等,其中,逻辑判别法需要给定一个测值的逻辑合理范围,不同监测效应量的合理范围不同,不具有普遍性。统计判别法适用于荷载条件变化不大的监测数据中,单纯使用统计判别法的误差检测率往往不高。基于模型的方法需根据环境量等信息建立相应的预测模型,以模型预测值和实际测值的残差为检测对象,根据统计学方法或者机器学习方法进行异常值检测,该方法是一种有监督学习方法,对粗差等异常值检测的精度受限于所建模型精度,而所建模型精度往往又受异常值的影响,因此用于建模的样本数据往往需人工审核去除异常值,没有达到减少人工工作量的效果。本文提出一种基于数据重构与孤立森林法[8](Iso⁃lation Forest)的异常数据检测方法,这是一种无监督的学习方法,适用于连续型的时间序列数据。
孤立森林算法是由刘飞博士在陈开明、周志华教授指导下提出的一种基于集成学习的快速异常检测方法,算法因具有高精准度、无监督等优点,被广泛应用于大数据的异常值检测[9,10]。由于孤立森林算法不适用于有趋势性变化的数据序列,因此需要先对数据序列进行分解与重构,将趋势项分离出来,剩余项作为孤立森林训练和异常检测的样本。为此,本文利用小波变换[11]、快速傅里叶变换[12]、奇异谱法[13]对监测数据进行分解与重构,以分离出趋势项,需要说明的是,这三种趋势性分离方法适用于时间连续且不存在趋势性误差的时间序列,此外,时间序列样本越长,分离出的趋势项精度越高。为进一步消除异常值和毛刺点,经孤立森林法进行异常值剔除后,对其余测点采用拉依达准则(Pauta criterion)进行异常值检测。
1 大坝自动化监测数据分解与重构
大坝监测自动化数据异常检测的前提是将监测数据的趋势项分离出来,为此,本文利用小波变换、傅里叶变换和奇异谱法对监测数据进行分解与重构。
1.1 小波变换
对于一维数据样本x(n)(n= 0,1,…,N- 1),采用小波进行分解,x(n)可分离出高频信号和低频信号。设P0=x,则第j层上的一维离散小波可表示为:

式中:Pj为低频序列;Qj为高频序列;cAj为低频系数;cDj为高频系数,(j= 1,2,…,L,k= 0,1,2,…,N/2j- 1);L为小波分解的层数;φ为尺度函数;ψ为小波基函数。式(1)可形象表述如图1所示。
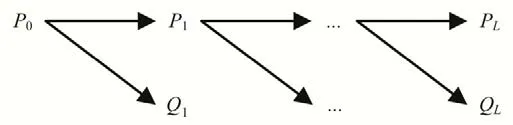
图1 小波分解示意图Fig.1 Wavelet decomposition diagram
小波重构算法与分解算法相反[14],小波分解出的高频序列Qj可视为噪音,经过多层分解后,可分离出表征时间序列数据变化规律的主分量,本文采用第L层低频近似部分和高频细节部分模拟数据样本的趋势项xc(n),即:

1.2 傅里叶变换
对于一维数据样本x(n)(n= 0,1,…,N- 1),式(3)称为x(t)的傅里叶变换。
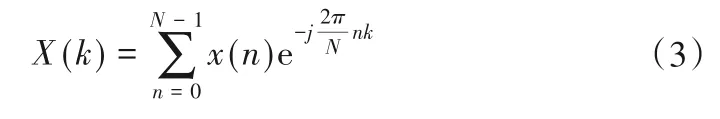
式中:X(k)称为x(n)的第k层频谱函数。
时间序列x(n)经过傅里叶变换后失去时间特性,即X(k)仅具有频率特性,X(k)由x(n)在时间序列上的特性决定。
本文以高斯函数滤波[15]为低通滤波器,以通过高斯滤波器后输出的时域信号模拟数据样本的趋势项xc(n)。
1.3 奇异谱
奇异谱分析是由Broomhead 等[16]提出的一种适用于非线性、非平稳信号的分解与重构方法,具有计算工作量小的优点[17]。
对于一维数据样本x(n)(n= 0,1,…,N- 1),假设嵌入的维数为m,时间延迟为τ,则数据样本嵌入m×l维相空间为:
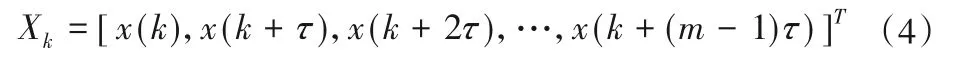
式中:k= 1,2,…,l;l=N-(m- 1)τ;X=[X1,X2,…,Xl]代表m×l维相空间的l个映射点。
令C为X的m×m维协方差矩阵,则:

通过对协方差矩阵C进行奇异值分解,可得到一组非负的奇异值(ei,i= 1,2,…,m),按e1≥e2≥…≥em≥0 排列组成奇异谱。其中大的奇异值对应信号中的有效成分,小的奇异值可视为信号中的噪声。
ek对应的特征向量Ek称为经验正交函数(EOF),第k个主分量定义为样本序列x(n)在Ek上的正交投影系数:
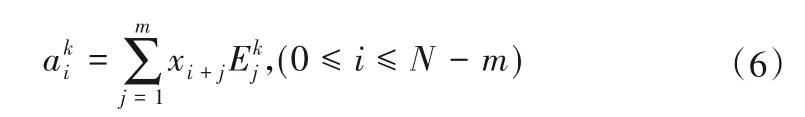
当Ek和已知时,重构的样本信号如下:
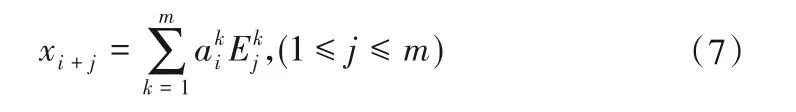
本文采用第1主分量重构的样本信号模拟数据样本的趋势项xc(n)。
2 孤立森林算法
孤立森林(iForest)算法的提出是基于异常点的两个特征[18]:分布稀疏以及离密度高的群体较远,具有上述特征的点也被称为容易被孤立的点。针对一组连续型的数据集,孤立森林算法的核心在于随机进行采样并构造一定数量的iTree,由这些iTree组成一个iForest。构造iForest的主要步骤如下:
(1)本文以分离趋势项后的剩余项的绝对值即|x(n) -xc(n)|为训练集,越靠近0 则该数据点是正常点的概率越大,为此建立一组用于训练的样本集g={g1,g2,…,g2N},gi=-gi+N= |x(i) -xc(i)|,从样本集中随机选择m个样点作为子采样集D={d1,d2,…,dm},作为树的根节点。
(2)从当前子采样集中随机一个分裂点p,p介于当前子采样集中最小值到最大值之间。
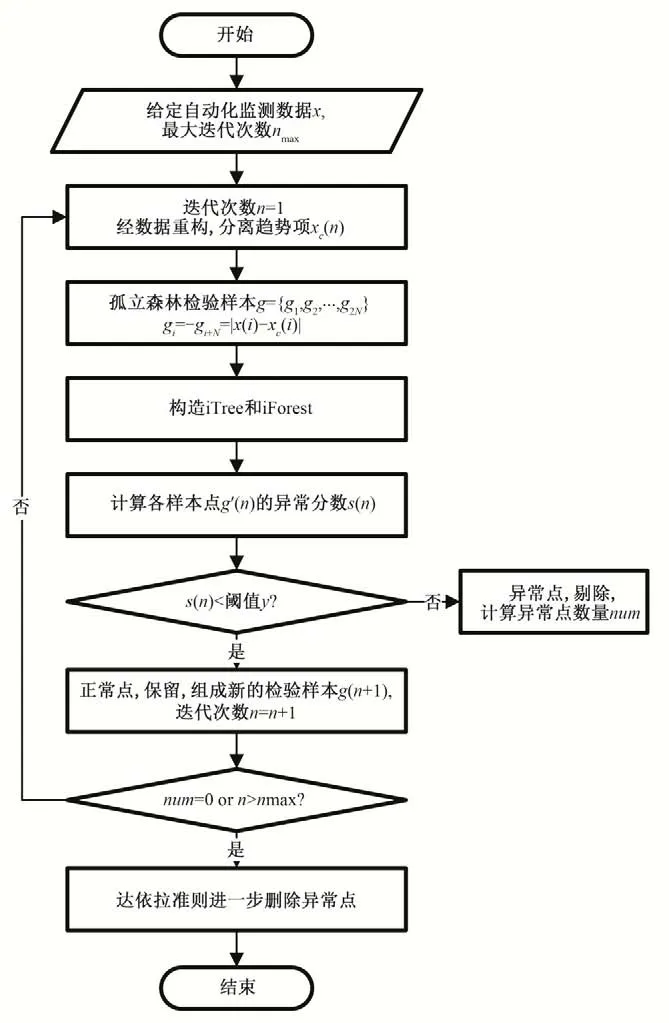
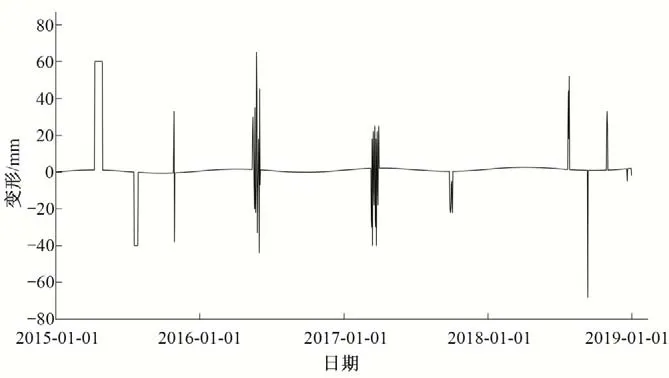
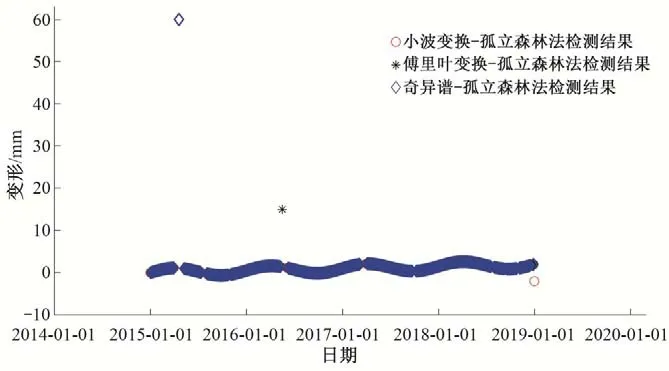
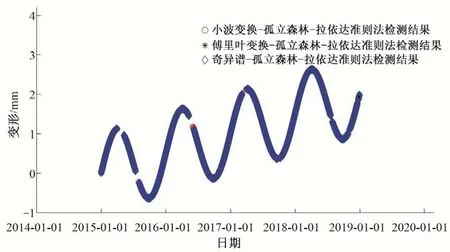
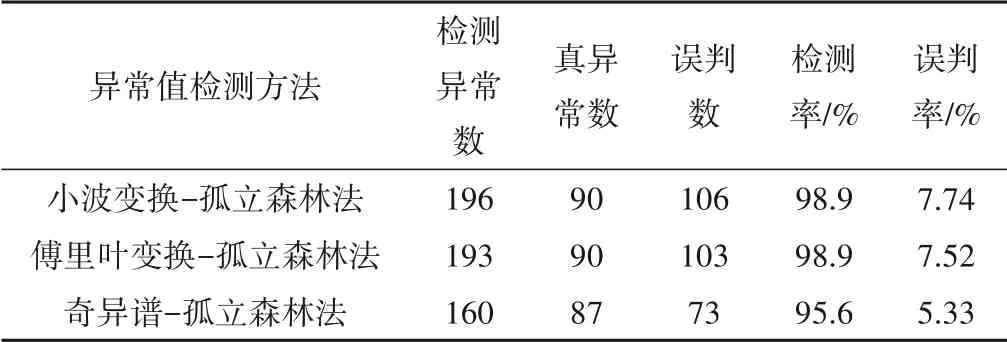
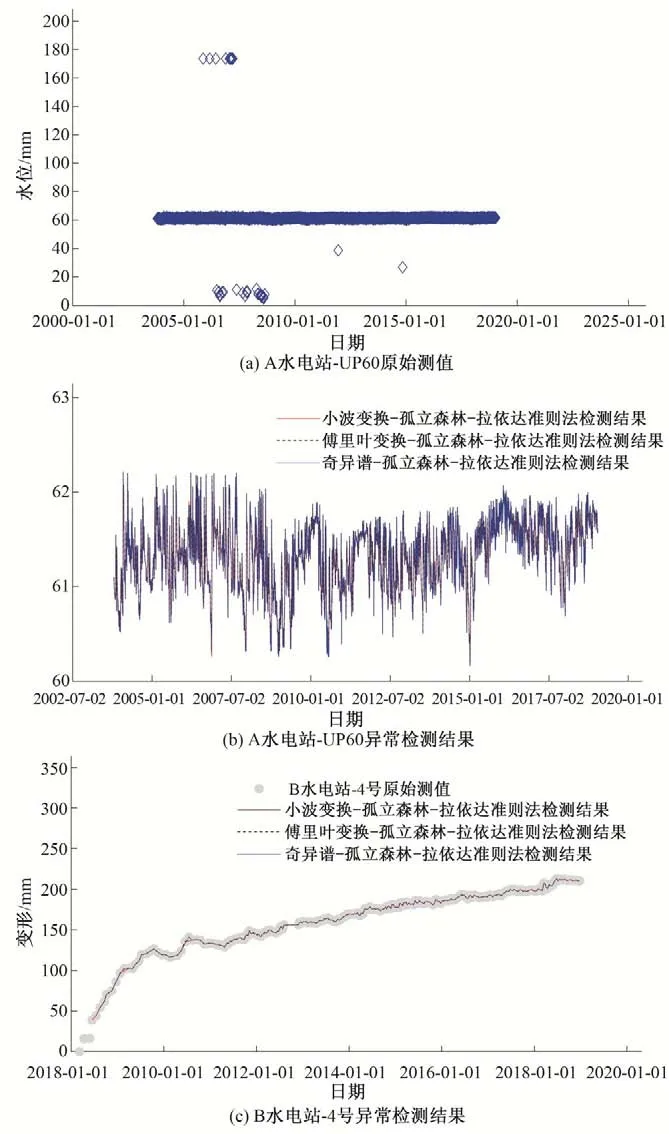
(3)对子采样集的每个数据di,若di (4)重复步骤(2)、(3),不断构造新的左、右子树,直至满足下列条件之一:①D中只有一个数值或者N个一样的数值,无法进一步划分;②树的高度达到限值。 (5)重复上述步骤,直至iTree 的数目达到限值,由这些iTree组成一个孤立森林。 对任何一个查询数据x,通过循环一次孤立森林里所有树,可以计算该查询数据在每一颗iTree的路径长度h(x),进而可以计算在该孤立森林里路径长度的期望E[h(x)]。对于提供含有m个样本数量的子样集D,由于iTree 的结构与二叉树等价,因此其搜索路径长度平均值c(m)等价于二叉树中失败查询的路径长度[18],文献[19]给出了二叉树中失败查询的路径长度: 式中:H(m-1)为调函数,可以被估计为H(m-1)=ln(m-1)+γ,γ为欧拉常数;c(m)作用为标准化查询数据x的路径长h(x)。 查询数据x的异常分数s计算公式如下: 查询数据x根据如下准则进行异常检测:当E[h(x)]→c(m)时,s→0.5,不能判断查询数据x是否为异常;当E[h(x)]→0 时,s→1 时,被检测为异常点;当E[h(x)]→m- 1时,s→0时,被检测为正常点。 拉依达准则通过计算标准偏差判断测值偏离整体的程度,当偏离程度超出允许区间时,认为该测值为粗大误差,需要注意的是使用拉依达准则需要足够多的样本,当样本数较少时,其剔除粗大误差的准确性会降低。为进一步消除粗大误差,经孤立森林法进行异常值剔除后,对其余测点,若剩余项小于指定值,由于剩余项为无趋势性的平稳时间序列,可通过拉依达准则方法对异常值进一步进行检测。综合上述理论,基于数据重构和孤立森林法的大坝自动化监测数据异常检测的流程如图2。 图2 算法流程图Fig.2 Algorithm flowchart 为验证算法的可行性,构造一组含异常值的大坝变形时间序列,该序列从2015年1月1日至2018年12月31日,共有1 461 个数据测点,其中异常值91 个,占总测值的6.22%,见图3。 分别用小波变换-孤立森林法、傅里叶变换-孤立森林法、奇异谱-孤立森林法对图3 测值进行异常检测,其中iTree 样本容量为256,最大层高为8层,森林里共计有100颗iTree,最大迭代次数为50 次,异常分数判别阈值y选取将影响到算法的检测率,若取值过大,则多数异常值不能检测,反之,则误判率较高,故本文按式(10)取值,阈值y先小后大。 图3 含异常值时间序列Fig.3 Time series with outliers 式中:c1表示阈值初始值,实际取值时可先取0.50,根据实际情况进行调整;c2为参数,文中取1.0;n为当前迭代次数。 各算法检测效果见表1、图4 和图5。由图表可见,各算法的异常值检测率均在95%以上,小波变换和傅里叶变换的检测率大于奇异谱法。误判率均在8%以下,奇异谱法的误判率最低,误判点主要出现在连续出现异常值的区域。由图可见,对于具有趋势性和周期性变化的时间序列测值,本文的三种方法均具有较高的检测率,再经拉依达准则判别后,基本能消除异常值带来的影响。 图4 各算法异常检测结果Fig.4 Abnormal recognition curves of different algorithms 图5 各算法与拉依达准则异常检测结果Fig.5 Abnormal recognition curves of different algorithms and Pauta criterion 表1 各算法异常检测成果表Tab.1 Abnormal recognition results of different algorithms 大坝自动化监测数据异常值大小、数量以及分布规律要复杂得多,为进一步验证本文算法的有效性,以两个大坝工程自动化监测数据进行异常检测。其中A 水电站大坝位于福建闽江,最大坝高101 m,坝顶长783 m,对其绕坝渗流测点UP60 监测数据进行异常值检测。另一水电站大坝B 位于云南省南盘江,最大坝高96.5 m,坝顶长456.8 m,对坝体内部沉降测点4 号自动化监测数据进行异常值检测,该数据无明显异常点。 检测成果见表2和图6。A 水电站绕坝渗流测点UP60共有8 527 个数据,由于异常值存在,无法判断绕坝渗流孔水位测值情况,剔除异常点后,该绕坝渗流孔测值在60~62.5 m 之间,无明显趋势性变化。B 水电站大坝内部沉降变形测点4 号共有306 个数据,测点测值无明显异常点,但由于测值初期,测值较少且变化较大,初期测值被误判为异常点。通过数据重构-孤立森林-拉依达准则法进行异常检测后,基本能消除异常值带来的影响且误判率整体较低,能够满足工程实际应用。 图6 大坝自动化监测测点异常检测成果Fig.6 The results of abnormal detection of the dam automatic monitoring points 表2 典型测点异常检测成果表Tab.2 The results of abnormal detection of the dam typical points 本文利用小波变换、傅里叶变换和奇异谱法对时间序列数据进行分解与重构,提取出趋势项后通过孤立森里法对剩余项进行异常检测,最后根据拉依达准则法进一步提出异常值。将组合数据重构-孤立森林-拉依达准则法的组合算法用于大坝自动化监测数据异常检测中,得到以下结论。 (1)本文的组合方法是一种无监督学习,除时间序列以外不需其他特征标签,不需要对训练样本进行学习,扩大了其适用范围,降低了工作量。 (2)通过数据重构-孤立森林-拉依达准则法进行异常检测后,基本能消除异常值带来的影响且误判率整体较低,能够满足工程实际应用。 (3)误判点主要出现在连续异常值出现区域的相邻正常测点,这主要是因为小波变换、傅里叶变换和奇异谱法重构分离出的趋势项受连续异常值的影响,因此对于时间不连续、测值少且变化剧烈的时间序列适用性不强。□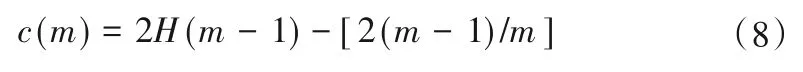

3 实例分析
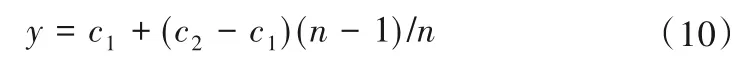

4 结论
——以徐州高层小区为例

