基于格子Boltzmann方法的三维溃坝数值模拟

邵 晨，黄剑峰

（云南农业大学水利学院，昆明650201）

0 引言

溃坝是一种灾害性的水流现象，其洪峰流量、运动速度、破坏力远大于一般暴雨洪水或融雪洪水。除了其超标准洪水、冰凌以及地震等致大坝溃坝的自然因素外，还有设计不周、施工不良以及管理不善等人为因素。溃坝的破坏力会带来巨大损失［1］，所以溃坝数值模拟就显得尤为重要，模拟结果不仅可以分析水流的流动过程，还可以用于推演坝前设置不同障碍物的消能效果，而且能够对溃坝生命损失进行估算［2］。

计算流体力学（CFD）可以在虚拟环境中仿真分析流体流动情况，降低了时间和成本，是一种可以代替实验研究的手段。传统的求解Navier-Stokes 方程的CFD 解算器一般都是基于网格的求解方法，因此需要经过一个耗时的网格划分过程，网格质量不仅制约着数值解的稳定性，而且影响着解的质量，且若干等尺寸的网格会提供不同的解，这会给解带来不确定性。大多数传统的编码通过加入人为的数值黏度来确定解，这种黏度会很大程度上改变和抑制解的稳定性，并且对非恒定流和声学的精度有很大的负面影响。如果不考虑一些简化和假设，那么Navier-Stokes方程是没有解析解的，而且由于计算的限制，它们的直接数值模拟（Direct numerical simulation）在实际工程中几乎是不可能的，所以仅限于学术应用，因此需要建立模型。然而，像雷诺平均方程（RANS）湍流模型都是经验模型，它们的缺点是依赖大量常数，为了正确地模拟湍流就要必须仔细校准这些常数。发展的大涡模拟（LES）湍流模型因其与使用Navier-Stokes 求解器的RANS 模型相比计算成本较高，所以并没有得到广泛的应用。LBM 是一种介于宏观与微观之间的介观方法，它不考虑单个粒子的运动，而是将所有粒子的运动视为一个整体，它同时具有微观方法和宏观方法的优势，其更擅长处理复杂边界，具有良好的并行性，且其获取压力场的方式不像传统N-S 方程需要大量计算求解泊松方程，LBM 是通过计算流体状态方程获得压力场。通过LBM 模型在处理破碎交界面的优势与VOF相结合，可以更好的观察到液体的飞溅及破碎。

为了对溃坝后水流的流动过程进行数值计算，开发出如SPH 法［3］等二维模型，该方法能简便、快速、有效地进行数值模拟。宁聪等［4］利用二维模型对不同闸门开度下溃坝水流的淹没范围及最大流速进行了分析；刘慧玲等［5］利用SPH 方法对溃坝水流进行模拟，通过实验与数值模拟的溃坝水流外部轮廓进行比较，验证了SPH方法的准确性；SWEGLE等［6］发现SPH法存在着如自由表面的计算精度不够准确，计算应力时会出现计算不稳定等现象；陈薇等［7］根据改进的核函数和改进的动量方程的离散形式相结合后验证发现SPH 法稳定性和模拟效率都有明显提高；缪吉伦等［8］论述了SPH 法的基本理论并利用该方法模拟了溃坝水流冲击障碍物的飞溅及融合。对于进一步开发的三维模型，林长强［9］利用FLUENT 对土石坝逐渐溃坝水流模拟；曾丹等［10］在基于Flow-3D，采用RNGk-ε模型和VOF 法，建立了分析溃坝洪水的水流三维数学模型，模拟弯道溃坝洪水的演进过程，其计算精度与水流模拟的流动过程相对较好，但其又存在着需要复杂且耗时的网格划分等问题。近年来，基于最小动力学模型的Boltzmann 方程越来越受欢迎。LBM 方法最初是用于去除统计噪声并实现更好的伽利略不变性［11，12］，由于其与动力学理论的密切联系所提供的灵活性，LBM 方法可用于模拟多种物理现象，张建民等［13］对LBM 应用在多相流中的研究现状进行了综述，旨在进一步扩大LBM 方法在多相流研究中的适用性。本文将采用LBM 方法对瞬时全溃坝和局部瞬时溃坝进行数值模拟，并与前人的模拟实验结果进行比较，利用LBM 方法对瞬时溃坝时在坝前设置不同消能坎对其消能能力进行比较，并分析水流对障碍物的作用力，从而表明基于LBM 方法在溃坝数值模拟中具有很大的使用价值。

1 数值模拟方法

1.1 格子玻尔兹曼方法

格子Boltzmann 方法（LBM）是从格子气自动机（LGA）方法发展来的，与LGA 方案所使用的布尔逻辑不同的是，LBM 利用具有实变量的统计分布函数fi，通过构建质量守恒和线性动量来计算数据。

定义格子Boltzmann的输运方程如下：

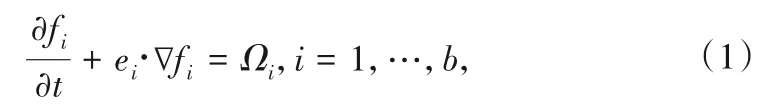
式中：fi是方向i上的粒子分布函数；ei是相应的离散速度；Ωi是碰撞算子。

LBM 的撞击流方法可解释为连续Boltzmann 方程的离散化。撞击流或传播步骤模拟的是粒子分布函数沿离散方向的平流，而大多数模型是由碰撞算子模拟的，碰撞算子对模拟的数值稳定性也有很大影响。最常见的方法是使用基于Bhatna⁃gar-Gross-Krook（BGK）近似的单弛豫时间（SRT），其定义如下所示：

式中：τ是松弛时间参数，与宏观黏度v相关［14］，如下所示：

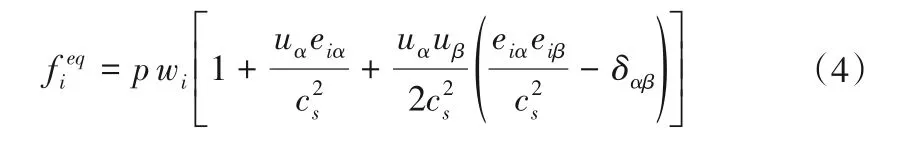
这里的cs是格子声速，p为流体密度，u是宏观速度，δ是克罗内克符号，α和β表示方程中出现的向量的不同空间分量，wi是为了保持各向同性而建立的加权常数，对于常用的三维格子离散速度模型D3Q19模型（见图1），有：

图1 D3Q19格子模型Fig.1 D3Q19 lattice model

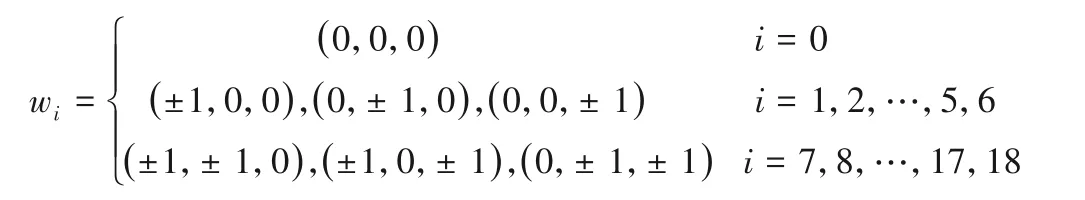
通过Chapman-Enskog 展开，可以证明所得到的结果可以重现低马赫数下的水动力状态［15，16］。单弛豫时间法因其简单而常被使用，但它不适用于高马赫数的应用，而且容易出现数值不稳定。用多弛豫时间（MRT）碰撞算子解决了BGK 的一些限制，其碰撞过程在矩形空间中而不是在通常所用的速度空间中进行，其定于如下：

另一种旨在克服BGK 方法局限性的方法是熵晶格Boltzmann（ELBM）方法，它可以依赖于单个弛豫时间，然而从计算的角度来看，这种方法特别昂贵，因此没有在实际工程应用中使用。中心力矩格子Boltzmann 方法中的碰撞算子是基于多重弛豫时间的方法。然而，与标准MRT不同的是散射算子是在中心矩空间中实现的。松弛过程是在一个移动的参考系中通过改变离散粒子的速度和局部宏观速度来实现的，这自然地提高了给定速度集的伽利略不变性和数值稳定性［19］。原始力矩可以定义为：

中心力矩定义为：

式中：ux，uy和uz是宏观速度的组成部分；µ为原始力矩；k、l和m分别为x、y和z方向上的力矩阶数。

1.2 湍流模型

湍流建模采用的方法是大涡模拟（LES）。该方法引入了一种附加的黏度系数ut，称为紊流涡流黏度Vt，以模拟亚网格湍流。本文使用的LES 模型是壁面适应局部涡流（WALE）黏度模型，该模型提供了一致的局部涡流黏度和近壁面行为。具体定义如下：

式中：∆f=Cw∆x是滤波尺度；∆x为单位网格尺度；S是分解尺度的应变率张量；常数Cw通常为0.325；u为动力黏度系数；δαβ为克罗内克尔符号；α，β，r为张量下标。

式中：y为与壁面的法向距离；x为与壁面相切的局部流动方向；uτ为表面摩擦速度；τw为湍流壁面剪应力；dpw/dx为壁面压力梯度的特征速度；u为离壁面给定距离处的平均速度；f1和f2为插值函数。

边界层的速度场是通过y+得到的；y+取决于第一个晶格从几何体壁y到第一个晶格的速度uc之间的距离。

1.3 VOF法

VOF 法是根据不同时刻单元网格内流体容积的改变实现对自由表面的追踪，其具体定义可描述为：假设存在某一流体ρ，某一时刻时流体ρ所占单元网格的体积函数为ɑ，当ɑ=1 时，则单元网格内充满流体ρ；当ɑ=0 时，该单元网格内无流体ρ；当0<ɑ<1时，则说明该单元处于气体与流体ρ交界面。

2 模型验证

本文采用所建立的三维模型对全溃坝和局部溃坝2个物理模型进行数值模拟，并将计算结果与杨哲豪等［21］数值模拟结果进行比较，验证分析模型的准确性。本文中默认取水的密度为ρ=1 000 kg/m3，采用牛顿黏度模型，动力黏度为0.001 Pa∙s，重力加速度为9.81 m/s2。

2.1 瞬时全溃坝

参考Al-Faesly等［22］几何模型，建立封闭的几何箱体进行数值模拟。瞬时全溃坝数值模拟俯视图如图2所示，采用长5.6 m，宽2.7 m，高为1 m 的矩形箱体作为水坝储水，下游水槽设置为长为14 m，宽为1.32 m，高为1 m 的矩形箱体，因对比实验采用的是下游末端水槽为开边界，为了保证实验的准确性对下游水槽的封闭边界进行了适当加长。此外，实验还设置了两个传感器来监测溃坝时洪水的高度。水坝的初始水位设为0.85 m，模拟时间为8 s，模拟精度为0.05 m，溃坝方式为瞬时溃坝。

图2 全局瞬时溃坝数值模拟俯视图（单位：m）Fig.2 Top view of numerical simulation of global instantaneous dam break

通过数值模拟水流的流动过程，结果如图3所示。水体在初始位置时开始向下游水槽流动，在重力加速度的作用下，溃坝水流在流动过程中的速度形成了非常鲜明的分层现象。从图3（a）看到水流到达了传感器1 的位置，从图3（b）看到在3.16 s洪水到达左壁面，由图3（c）看到在4.12 s时击打左壁面后水流飞溅形成一定高度的水舌。

图3 瞬时全溃坝水流的流动过程Fig.3 The flow process of global instantaneous dam break

在传感器1 监测溃坝时洪水的水位高度变化，通过记录水位高度变化的并与文献［21］进行比较，对比结果如图4（a）所示。在本文所建立的三维模型下进行数值模拟，计算结果到达传感器1监测点位置的时间与文献［21］实验到达监测点的时间更相近，二维数值模拟下水流到达传感器1 的时间略早于实验到达的时间，由于实验中水泵一直运作导致模拟过程中水位下降比实验更快，所以模拟结果存在一定的偏差。图4（b）中8 s内传感器2监测点的水位变化计算结果与文献［21］计算结果基本相同，可以看出本文的模拟结果更接近实验中水位下降高度的监测数据。通过图4 数据结果表明基于LBM 的方法在溃坝数值模拟计算中是准确的。

图4 相同时间内水位变化比较图Fig.4 Comparison of water level changes in the same time

2.2 局部瞬时溃坝

上文验证了瞬时全溃坝的准确性，为了进一步验证模型在局部瞬时溃坝时的准确性，本文根据Aureli 等［23］的局部溃坝物理模型，建立封闭的几何箱体进行数值模拟。局部溃坝的数值模拟俯视图如图5所示，设立一个长2.6 m，宽1.2 m，高1 m 的封闭箱体，设水库初始水位为0.1 m，水库长0.8 m，宽1.2 m，在水坝中央位置设置0.3 m 宽大坝以达到局部瞬时溃坝的目的。在离水坝0.5 m 下游处设置一长0.155 m，宽0.3 m，高0.2 m 的矩形箱体障碍物，并在适当位置设置两个速度传感器，模拟时间为1.5 s，模拟精度为0.009 m。

图5 局部溃坝的数值模拟俯视图（单位：m）Fig.5 Top view of numerical simulation of local dam break

通过LBM 方法对局部溃坝进行数值模拟并选取四个不同时刻，与文献［21］现场实验和计算水深云图进行比较，如图6所示。图6（b）可以看出在0.38 s 水流到达障碍物，图6（c）看出在水流接触到障碍物位置的水深明显爬升，在图6（d）中水流绕障碍物向两侧流动。在LBM 方法的数值模拟中，VOF下呈现的模拟结果与文献［21］实验拍摄图形与计算云图吻合较好，表明LBM方法可以准确的模拟局部瞬时溃坝水流的流动情况。

党的十八大报告提出，要实施创新驱动发展战略，强调科技创新是提高社会生产力和综合国力的战略支撑，必须摆在国家发展全局的核心位置。这充分表明了我们党依靠创新实现经济持续健康发展的坚定决心和对科技创新的高度重视。当前，东营市正处于全面实施黄蓝国家战略，加快推进“率先全面建成小康社会、率先建成生态文明典范城市”（两个率先）建设目标的关键时期，对科技进步和创新提出了更加全面、更加紧迫的需求，必须深刻认识并充分发挥科技创新的支撑引领作用，制定和实施创新驱动战略，完善区域科技创新体系，全力依靠创新驱动提高发展的质量和效益。

图6 局部溃坝数值模拟对比图Fig.6 Comparison of numerical simulation of local dam break

为了比较不同位置的速度变化，对不同位置传感器的速度进行计算，结果如图7所示。由图7（a）传感器速度的变化可以看出，溃坝水流在0.38 s左右到达传感器位置，流速陡然上升到0.155 m/s，随后水流到达障碍物后速度急剧下降，这是由于障碍物的阻碍作用；在0.6～0.78 s 流速随着溃坝水流演进流速加快；在0.78～0.96 s 随着障碍物上游水深爬升，流速逐渐变慢；0.96～1.04 s 障碍物上游储存的水开始向两侧流动，流速随之增大。图7（b）可以看出水流在0.52 s 到达传感器4 流速陡然上升到0.85 m/s，在1.08 s流速达到最大；当溃坝水流撞击障碍物后，水流从障碍物的两侧向下游流动，通过比较可以看出图7（b）水流的速度大于图7（a），这和实际中结构两侧水流速度快相符。

图7 不同位置传感器速度变化图Fig.7 Velocity variation of sensors at different positions

为了进一步研究局部溃坝水流对障碍物的作用力，对1.5 s内水流对障碍物的作用力进行计算，结果如图8所示。水流在0.38～0.9 s撞击障碍物然后绕障碍物开始流动，因水流对障碍物的不断撞击，其作用力变化剧烈；水流在0.9～1.5 s 已包裹住整个障碍物，水流的流动也趋于平缓，水流对障碍物的作用力变化剧烈程度变小。水流对障碍物冲刷的作用力变化剧烈程度体现了水流流动的不稳定性，而在文献［21］中利用二维数值模拟所计算出的溃坝洪水对障碍物的冲击荷载曲线图相对平滑，不能体现出由于洪水对障碍物的剧烈冲刷所带来的冲击荷载的剧烈变化程度。

图8 水流对障碍物的作用力Fig.8 Force of flow on Obstacles

3 两种消能坎的溃坝流动模拟

通过与前人实验比较后可证明基于格子Boltzmann 方法的准确性，利用该方法分别模拟无孔障碍物和有孔障碍物两种情形下的自由表面流动现象。参考刘维平等［24］几何模型，在离封闭箱体左侧0.6 m 处布设了一个障碍物，通过比较两种模型中水流撞击障碍物及壁面时的压强，分析两种障碍物的消能效果。

无孔障碍物与有孔障碍物模型侧视图模型布置如图9所示，建立一个长1.2 m，宽0.8 m，高1.2 m 的封闭箱体，在箱体左壁离右侧0.6 m 处设置一个长0.1 m，宽0.8 m，高0.2 m 的矩形无孔障碍物，如图9（a）所示。在其他条件相同的情况下，在障碍物上设长0.1 m，宽0.8 m，高0.06 m 的孔径，图9（b）所示。水体密度为ρ=1 000 kg/m3，采用牛顿黏度模型，取用动力黏度为0.001 Pa∙s，重力加速度为9.81 m/s2，溃坝方式为瞬时溃坝，模拟时间为0.9 s，模拟精度为0.01 m。

图9 无孔障碍物与有孔障碍物模型侧视图（单位：m）Fig.9 Side view of nonporous and perforated obstacle models

相同时刻两种不同消能方式的水流流动运动情况如图10所示。在瞬时溃坝后水体发生移动，水体撞击障碍物后向上飞溅。在t=0.14 s时，水流到达障碍物，在0.3 s时明显可观察到水流拍打障碍物激起水浪。无孔障碍物水舌飞溅高度最高达到1.2 m，有孔障碍物的水舌飞溅高度达1 m，速度的变化会引起数值模拟中流体颜色的不同，可以观察到无孔障碍物水流速度更快，加之飞溅后水舌的高度过高，考虑到下落过程重力势能的影响会导致其破坏性更强。

图10 相同时刻两种消能方式水流运动对比Fig.10 Comparison of flow motion of two energy dissipation methods at the same time

选取2个典型时刻两种消能坎的VOF 等值面如图11所示。从图11（a）可以看到水流在撞击障碍物飞溅到一定高度后波浪发生破碎，从图11（b）和图11（c）看到在水流撞击壁面后波浪再一次发生破碎，通过等值面中水流跃起形成的水舌高度以及波浪的破碎程度看出有孔障碍物消能效果更明显。

图11 两种消能坎的VOF等值面图Fig.11 VOF isosurface of two kinds of energy dissipation sills

为了验证经过有孔障碍物与无孔障碍物时两种消能坎的消能效果，分别在壁面不同高度设置了传感器监测水流冲击壁面的压强，水体撞击壁面的压强比较见图12所示。通过比较可见无孔障碍物产生的压强更大，因此可在消能障碍物上设置一定大小的孔隙，保证障碍物有更好的消能效果。

图12 水体撞击左壁面的压强比较Fig.12 Pressure comparison of water impact on left wall

为了比较水流对障碍物的作用力，对水流冲击障碍物时的作用力进行计算，结果如图13所示。分别对水流在有孔障碍物的上部结构与下部结构及无孔障碍物的作用力进行数值模拟计算，水流在0.14 s到达障碍物时，有孔障碍物的下部结构与无孔障碍物受到水流的作用力基本相同，无孔障碍物在0.2 s左右受到水流作用力达到最大，最大值为1 589 N。高于障碍物的水流在溃坝时由于重力加速度的作用，水流对障碍物作用力更大，在高于障碍物水流冲刷过后，水流对障碍物作用力的波动频率趋于稳定。根据图13的作用力对比结果，在相同的溃坝情况下，有孔障碍物抵抗洪水冲刷所需要的强度要求远小于无孔障碍物，无孔障碍物对结构的强度要求更高。

图13 水流对障碍物的作用力Fig.13 Force of flow on Obstacles

4 结论

本文在格子Boltzmann方法的基础上，采用LES模型和VOF法，建立了分析了溃坝水流分析的三维模型，通过一系列数值模拟得到如下结论。

（1）验证了该模型在瞬时全溃坝水流流动过程的准确性，本文方法与实验结果更相近在，在三维模拟下可以看到自由面流动情况，4.12 s 到达封闭箱体撞击左壁后可看到溅起一定高度的水舌。

（2）验证了该模型在局部瞬时溃坝水流流动过程的准确性，可以看到水流到达障碍物时，由于受到障碍物的阻挡，障碍物上游水流高度向上爬升，至一定高度后回落。随后，水流从障碍物两侧向下游运动；水流在向两侧变窄的河道流动流速加快，随着水流绕障碍物两侧向下游流动，水流对障碍物的作用力波动频率变小。

（3）通过模拟了两种不同消能坎的溃坝水流的流动情况，可以看到溃坝洪水冲击障碍物后水流飞溅的高度以及流动情况，通过压强的比较得出了有孔障碍物做消能坎时消能效果更好；通过VOF等值面的水流流动情况可以看到水流撞击无孔障碍物后波浪破碎程度更明显；有孔障碍物比无孔障碍物受到水流作用力削减了60%，水流对无孔障碍物冲刷的作用力比有孔障碍物更大。□