考虑偏转角度的钢筋石笼起动流速与拖曳力系数研究
朱文帅,吴 浩,徐杭杭,赵跃章,刘仲秋,李全起
(1.山东农业大学水利土木工程学院,山东泰安271018;2.山东龙跃兴设计集团有限公司,济南250014)
0 引言
抛投块石稳定问题一直以来都是关系着截流工程、河道工程成功与否的关键。钢筋石笼相比于传统散抛块石具有透水性良好、稳定性强、方便运输储存的优势,在截流领域得到了广泛的应用。
然而截至目前,国内外对于钢筋石笼抗冲稳定性的研究较少,实际工程应用缺乏可靠的理论指导,这对河道截流和抢险工作的设计和施工带来了不便。考虑到现有钢筋石笼抗冲稳定特性的研究大多以规则放置的石笼试块为研究对象,而实际的工程中并非所有的钢筋石笼在抛投沉底后都是严格按照顺水流方向静止,那么此时的钢筋石笼稳定性再以现有的研究成果去分析的话将存在误差。因此,针对现有钢筋石笼抗冲稳定研究的不足之处,通过受力分析与推导,提出了一种待定拖曳力系数的考虑偏转角度的钢筋石笼起动流速计算公式,并针对目前水下钢筋石笼拖曳力系数难以取值的现状开展了钢筋石笼拖曳力水槽试验,研究了偏转角度和雷诺数对钢筋石笼拖曳力系数的影响,给出了考虑偏转角度和雷诺数双因素交互影响下的拖曳力系数取值建议计算公式,为钢筋石笼抗冲稳定性的研究提供理论参考。
1 研究现状
现有的有关于块体抗冲稳定计算的研究大多脱胎于苏联截流专家伊兹巴什于20世纪30年代提出的经典截流块体起动流速计算公式[1],即:
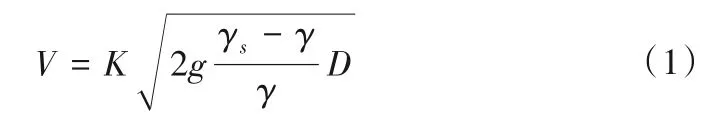
式中:V为截流块体的起动流速;K为稳定系数;γs为块体容重;γ为水的容重;D为块体的化引直径;g为重力加速度。
伊兹巴什公式及其类似公式虽然在实际工程应用中具有一定的计算精度,但其公式中所含变量较少,难以解释抛投块体因形状、河床垫层、水流攻角等因素变化而导致的起动流速的不同。针对上述问题,需要进一步加强石笼网结构抗冲刷特性的研究[2]。汪定洋等[3]结合多年的试验,提出了一种考虑相对粗糙度的块体起动流速计算公式,即
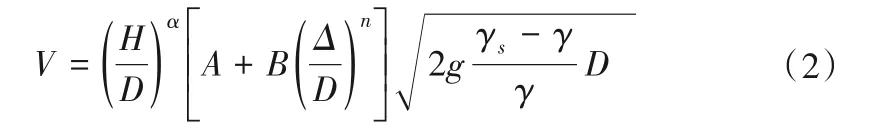
式中:H为水深;为相对粗糙度;α、n、A、B为待定参数,由具体试验确定。
李学海等[4]以公式(2)为基础,提出了考虑扁度系数的钢筋石笼起动流速计算公式,并通过试验对式中的α、n、A、B值进行了确定,即

式中:λ为石笼的扁度系数;a、b、c分别为长轴、中轴、短轴的长度。
郭红民等[5]考虑了石笼空隙率对起动流速的影响,并以公式(3)为基础引入了空隙度对公式进行了修正。然而以上各公式在底部为光滑面(忽略摩擦力)时难以适用,无法反应在忽略摩擦的情况下其起动流速接近于零的情况。另外,在形状不规则的长条形钢筋石笼情况下,化引直径D是否能适用并没有很好的理论依据,比如相同体积下的钢筋石笼,虽然化引直径相同,但其形状理论上存在无穷多种,即使是限制了其扁度系数,仍然存在多种的可能。基于以上公式的缺陷,叶恩立等[6]提出了一种以六面体长宽高代替扁度系数和化引直径的钢筋石笼抗冲稳定计算公式,解决了石笼在光滑面上起动流速的计算问题,其计算公式为:
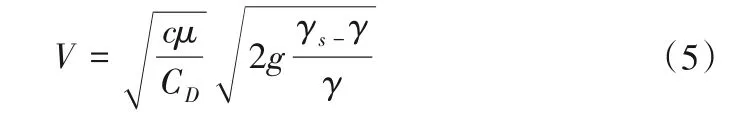
式中:c为六面体顺水流方向的长度;μ为地面摩擦系数;CD为钢筋石笼拖曳力系数。
伍学文等[7,8]以公式(5)为基础,通过数值模拟考虑了钢筋石笼空隙率与拖曳力系数CD的关系,拟合了考虑空隙率的钢筋石笼起动流速计算公式,具有一定的计算精度;汪淼等[9]结合公式(5)利用CD、CL云图对钢筋石笼的起动流速进行了研究,然而该文献结论与公式(5)都有一定的局限性,叶立恩等的试验仅研究了a×a×c形钢筋石笼的稳定性,伍学文等同样仅试验了a×a×a形的钢筋石笼,其公式都具有一定的局限性,并且公式(5)中的拖曳力系数CD的取值目前没有给出具体的取值计算方法,只能依靠工程经验取值。与此同时,考虑到工程实际中并非所有的钢筋石笼在抛投沉底后都是严格按照顺水流方向静止,随着钢筋石笼与来流方向成一定的夹角后,其迎流面积发生变化,那么此时钢筋石笼稳定性再按照以上结论进行分析同样将存在误差。
本文正是针对以上成果的不足之处开展了研究。
2 理论分析与公式推导
钢筋石笼在水下主要受到水流的拖曳力FD、重力G、浮力FV、阻力Ff、上举力FL。钢筋石笼的偏转方式如图1所示。实线矩形为长边c顺水流方向时的钢筋石笼俯视图,虚线矩形为钢筋石笼绕中心点O 旋转β角度时的俯视图,外圆为矩形对角边绕中心O点旋转的辅助轮廓线。
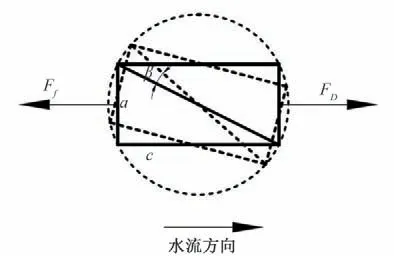
图1 钢筋石笼俯视面及旋转方式图Fig.1 Top view of steel gabion and rotation mode
如图2所示钢筋石笼收到来自顺水流方向的拖曳力FD,由于石笼顶部与底部流速存在差异,水流会给钢筋石笼一个向上的上举力FL。Eveet[10]于1987年给出了拖曳力计算公式(6)与上举力计算公式(7)。
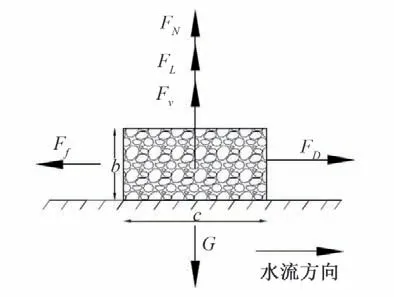
图2 钢筋石笼侧立面受力分析图Fig.2 Schematic diagram of force analysis on the side elevation of reinforced gabions
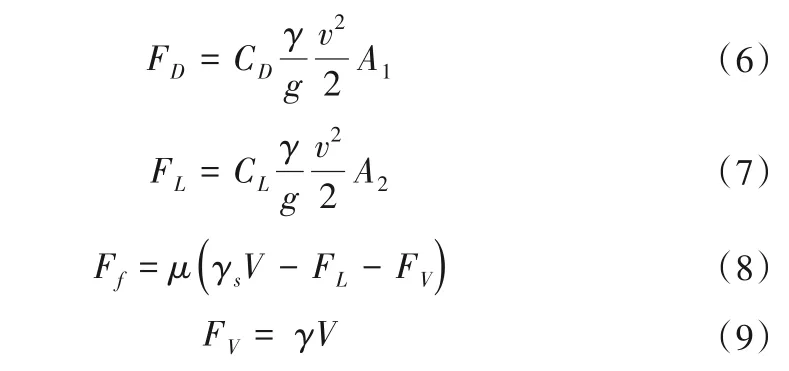
式中:A1、A2分别为钢筋石笼所受拖曳力和上举力的特征面面积。A1取值为迎流面的面积,当钢筋石笼如图1所示偏转角度β时,其特征面A1的取值为钢筋石笼底面对角线的长度在迎流方向上的投影与石笼高度的乘积,为钢筋石笼底面面积,A2=ac。
对绕中心O点旋转β角度后钢筋石笼进行受力分析,即FD=Ff,可得到待定拖曳力系数的考虑偏转角度的钢筋石笼起动流速公式:
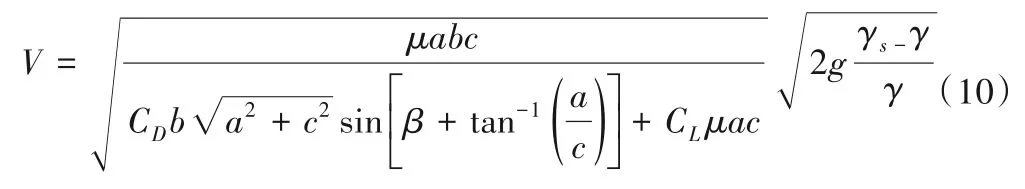
由式(10)可以看出,钢筋石笼的起动流速受到拖曳力系数、上举力系数、底面摩擦力、块体形状以及水流攻角等因素的影响。庞启秀[11,12]在对水下块体的受力试验中发现,块体所受上举力数据比较离散,且大小近似为零;Zhu L[13]等人的研究也证明了这一点。为方便计算,令上举力为零,得到简化后的钢筋石笼起动流速计算公式:

由所推公式(11)可以看出,当偏转角度β=0°时,式(11)可转化为公式(5)。与公式(5)相比,所推公式(11)适用于不同形状的六面体石笼,并且考虑了偏转角度对起动流速的影响,适用范围更广且考虑更为周全。又因为公式(11)中仅拖曳力系数CD为未知量,因此要通过试验来研究不同形状钢筋石笼的拖曳力系数CD的取值与雷诺数和偏转角度的关系。
3 模型试验及方法
3.1 试验模型与材料
本文分别设置了钢筋石笼的起动流速试验和拖曳力系数试验。两试验皆在1∶50 的水槽中进行,相似条件如表1所示。水槽试验段长10 m,宽40 cm,深40 cm,坡度为1/1 000,水槽两侧及为透明PVC 塑料板,底板为不透明PVC 塑料板,底板摩擦系数μ=0.22。

表1 起动流速及拖曳力系数试验相似条件Tab.1 Similar conditions of critical velocity and drag coefficient experiment
本次试验以高度为2 m 的钢筋石笼为原型,按照1∶50 比例制作了不同形状(a×a×a、a×a×c、a×b×c)三种形状的钢筋石笼,具体参数如表2所示。试验石笼的容重经查询相关文献[6,7]取为17.50 kN/m3。两试验的水面高度均维持在18 cm。

表2 试验钢筋石笼块材料参数Tab.2 Material parameters of test reinforced gabion blocks
3.2 钢筋石笼起动流速试验方法
起动流速试验方法:将试验石笼预先放置在渠道底部中间位置,然后开启阀门开关,调整流量大小,通过下游的尾门将水面高程控制在18 cm,直到试验石笼开始缓慢滑动。采用旋桨式流速仪,测量试验石笼迎水面中心处流速,当试块开始滑动时开始记录,共取6个流速值,计算时取其平均数。试块测完后将其绕底面中心分别旋转15°、30°、45°,重复以上步骤,直至测试完所有试块。
3.3 钢筋石笼拖曳力试验方法
Malavasi S[14]研究发现,当块体淹没程度够大时,拖曳力系数和上举力系数几乎不在随水深变化。Devarakonda R[15]的试验结论显示在块体与床面的距离大于0.13H后,拖曳力系数随相对位置的变化微弱。因此,为消除相对水深对试验结果的影响,试块距离床面的距离选择0.2H,即3.6 cm。
①通过无弹性的细钢丝线将试验钢筋石笼悬挂在距水槽底板3.6 cm 处,悬挂细线上部连接电磁感应拉力计。以钢筋石笼的宽、高面为迎水面,连接迎水面的细钢丝线穿过固定于水槽底板的定滑轮,定滑轮底部高度与钢筋石笼迎水面中心高度一致,穿过定滑轮底部的细线连接固定于水槽上方的电磁感应拉力计。②试验开始前对仪器进行调零,避免细线的摩擦、细线的重量对试验结果的影响。③通过流量调节阀门与下游尾门控制水位保持在18 cm,旋桨式流速仪测量水深与试块中心高程保持一致,控制水流流速分别为0.25、0.4、0.55、0.70、0.85 m/s。④记录电磁感应拉力计受到的拖曳力和上举力。⑤重复以上步骤,并将试块绕底面中心旋转15°、30°、45°重新进行试验,直至完成所有试块。钢筋石笼拖曳力试验如图3所示。
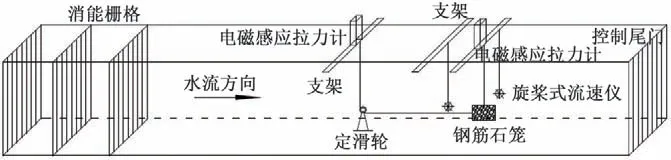
图3 钢筋石笼拖曳力试验测试系统Fig.3 Drag force experiment system
4 结果分析与曲线拟合
4.1 块体形状雷诺数对拖曳力系数的影响
块体雷诺数为流体惯性力与黏滞力的比[16,17],是用于表征流体绕流情况的无量纲,计算公式为:

式中:ρ为流体密度,kg/m3;U为平均流速,m/s;s为块体高度,m;μ为流体动力黏滞系数,Pa∙s。
由图4(a)~(c)可以看出,随着雷诺数的增大,a×a×a、a×a×c、a×b×c三种类型的钢筋石笼的水平拖曳力系数呈先增大后逐渐减小的趋势,同一钢筋石笼试块,不同偏转角度工况下,其水平拖曳力系数随雷诺数的变化趋势基本相同。雷诺数Res<2.2×104时,3 种类型的钢筋石笼的水平拖曳力系数均随雷诺数的增大逐渐增大;雷诺数Res处于2.2×104左右时,钢筋石笼的水平拖曳力系数较大;雷诺数Res>2.2×104时,水平拖曳力系数随着雷诺数的增大有逐渐减小的趋势。
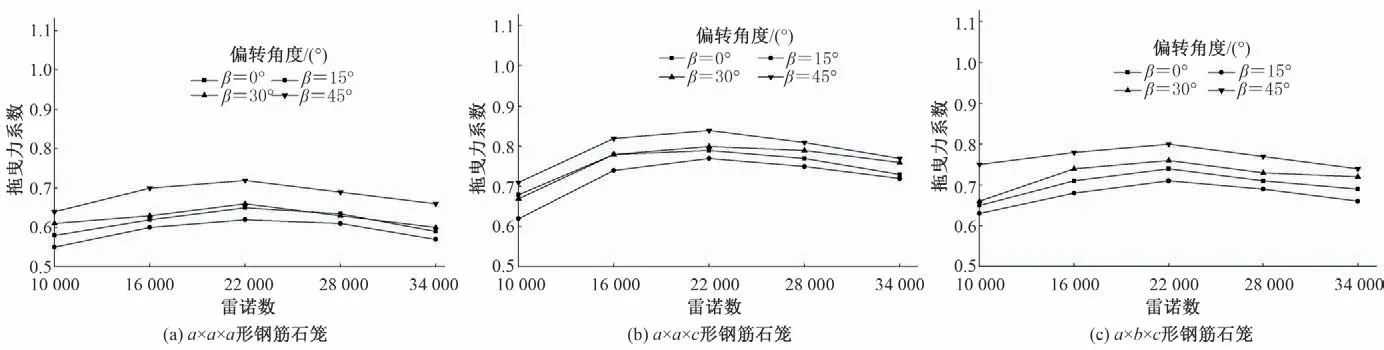
图4 拖曳力系数与雷诺数关系曲线Fig.4 The relationship between drag coefficient and Reynolds number
4.2 偏转角度对拖曳力系数的影响
由图5(a)~(c)可以看出,本次试验a×a×a、a×a×c、a×b×c三种类型的钢筋石笼的水平拖曳力系数变化值位于0.55~0.84 之间,a×a×c、a×b×c型的钢筋石笼的水平拖曳力系数明显大于a×a×a型的钢筋石笼。随着偏转角度的增大,钢筋石笼的水平拖曳力系数先减小后增大,当偏转角度达到15°时,水平拖曳力系数达到最小值。偏转角度大于30°时,a×a×c、a×b×c两种类型钢筋石笼的水平拖曳力系数增长变化率变缓,有趋于稳定的趋势。不同雷诺数工况下,3种类型钢筋石笼的水平拖曳力系数并不相同,但水平拖曳力系数随偏转角度的变化规律一致。

图5 拖曳力系数与偏转角度的关系曲线Fig.5 The relationship between drag coefficient and deflection angle
4.3 曲线拟合
考虑偏转角度和块体雷诺数的交互影响,根据图(4)、图(5)的试验数据可以假定钢筋石笼的拖曳力系数随偏转角度、块体雷诺数皆呈二次函数变化,利用双因素拟合的方法[18,19],导出待定系数的钢筋石笼拖曳力系数计算公式:
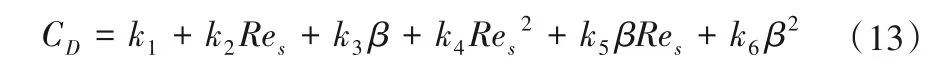
式中:k1,k2,k3,k4,k5,k6为方程的待定系数。
根据试验数据,利用最小二乘法[20],分别拟合a×a×a、a×a×c、a×b×c三种钢筋石笼的拖曳力系数计算公式,拟合后的计算公式分别为:

式(14)~(16)拟合优度R均达到0.85 以上,均为高度相关。图6为各类型钢筋石笼的拖曳力系数拟合曲面,可以明显看出,钢筋石笼的拖曳力系数随偏转角度的增大呈先减小后逐渐增大的趋势,随雷诺数的增大呈先增大后减小的趋势。

图6 钢筋石笼拖曳力系数拟合曲面Fig.6 Fitting surface of drag coefficient of reinforced gabion
将公式(14)~(16)代入推导所得的公式(11)便可得到考虑偏转角度、块体雷诺数、块体形状的钢筋石笼起动流速计算公式,即:
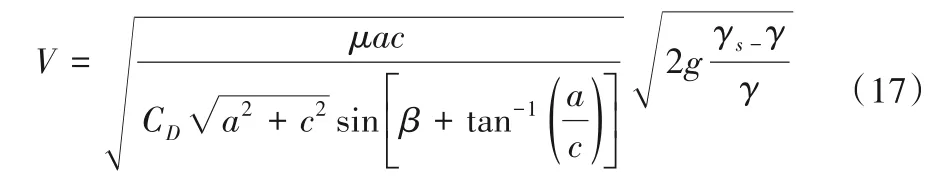
公式(17)起动流速的适用于六面体钢筋石笼,适用流速范围为1.77~6.00 m/s。a×a×a、a×a×c、a×b×c形的拖曳力系数CD的取值分别取式(14)、(15)、(16)。
5 起动流速公式的验证
拟合后的钢筋石笼起动流速计算公式计算值与水槽试验得到的起动流速进行对比,对比结果见表3。由表3 可知,由公式(11)、(14)、(15)、(16)计算得到的钢筋石笼起动流速与水槽试验实测值的最小偏差为0.35%,最大偏差为6.67%,所推导公式具有一定的精确程度,可为不同形状的六面体钢筋石笼抗冲稳定计算提供理论指导。
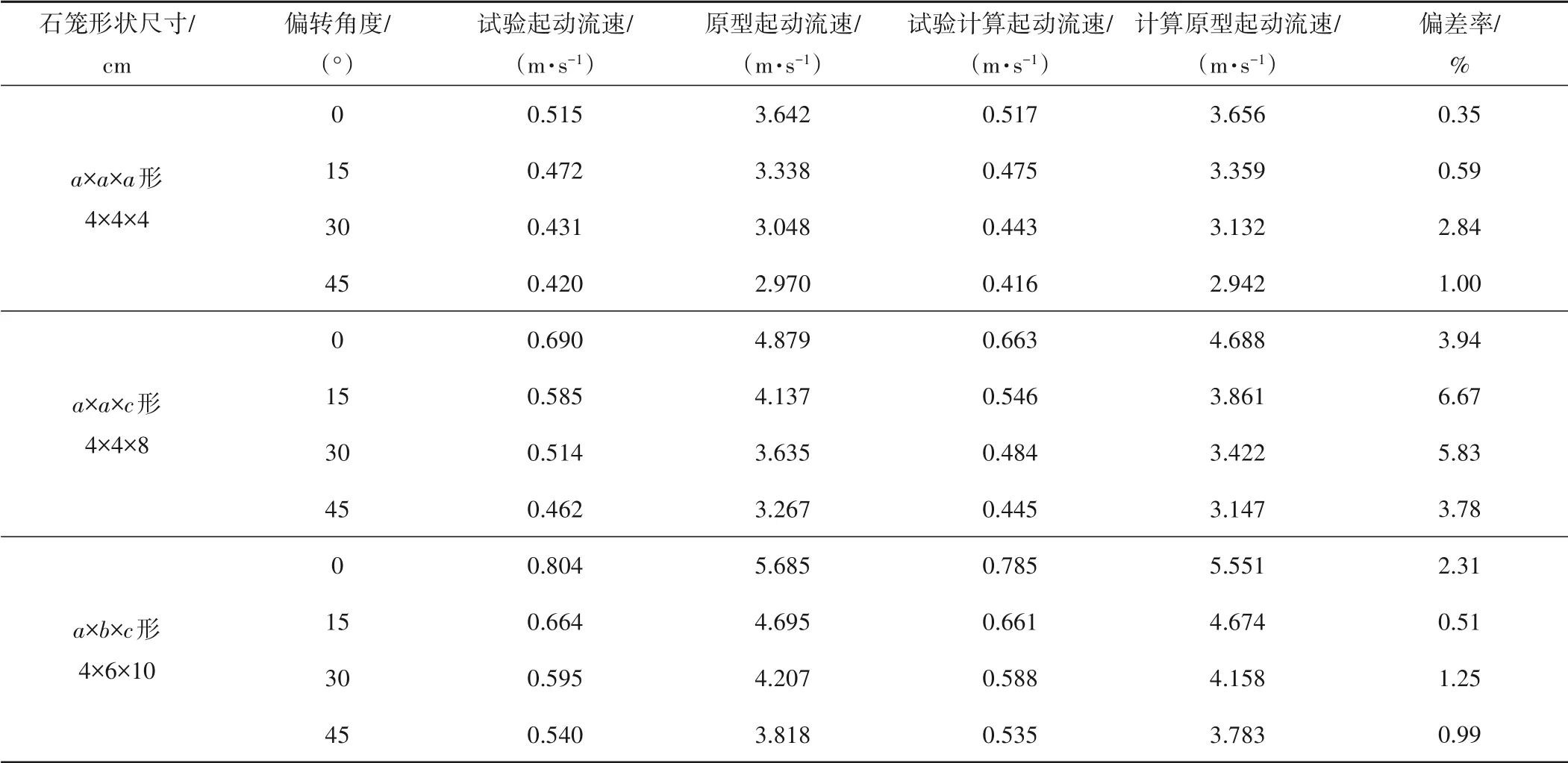
表3 钢筋石笼起动流速计算公式验证试验Tab.3 Verification test of critical velocity correction formula for reinforced gabions
6 结 语
笔者针对现有钢筋石笼起动流速计算研究的不足之处,提出了一种考虑偏转角度的待定拖曳力系数的钢筋石笼起动流速计算公式(适用于1.77~6.00 m/s 的来流流速),开展了钢筋石笼拖曳力水槽试验,研究了偏转角度和雷诺数对其拖曳力系数的影响,并对考虑偏转角度和雷诺数双因素影响下的拖曳力系数CD的取值计算公式进行了拟合。相比于传统的起动流速经验公式和依靠工程经验选取拖曳力系数的不利条件,该公式组合具有良好的理论性和准确性。本文通过试验还得出了以下结论。
(1)试验钢筋石笼的拖曳力系数变化范围基本处于0.55~0.84 之间,拖曳力系数随偏转角度和块体雷诺数的变化明显;
(2)钢筋石笼的起动流速随偏转角度增大而减小,水平拖曳力系数随偏转角度的增大呈先减小后增大的趋势;当偏转角度为15°时,拖曳力系数最小;
(3)随着雷诺数的增大,钢筋石笼的拖曳力系数先增大,后逐渐减小;当雷诺数Res在2.2×104左右时,拖曳力系数取值偏大。□

