施工分期导流围堰冲刷的清水动床模型设计

何志亚，冷月华，杨 磊，李修妍，李 博

（1.云南省红河州水利水电勘察设计研究院，云南蒙自661100；2.水资源与水电工程科学国家重点实验室（武汉大学），武汉430072；3.中工武大设计研究有限公司，武汉430072）

0 概述

水利水电工程建设中，施工导流是重要的一个环节。导流工程通常分为若干期进行，一期导流经常采用缩窄河床的方式，二、三期导流采用明渠、隧洞、底孔导流和联合导流方式。导流工程模型试验的任务主要是：确定分期导流方案、导流工程规模、体型、消能防冲、航运及漂木等。其中，一个主要课题是泄流规模问题，它决定着导流工程的规模和布置；另一个重要问题是流速分布和大小，它决定着导流工程的防冲措施和保护部位［1，2］。

与河工或单项泄水建筑物的水流模型相比，施工导流模型具有如下特点［2-4］：

（1）由于模拟对象包括所有枢纽建筑物和从上游到下游一个河段，因而必须通过整体模型进行试验研究；而且由于纵向和横向模拟范围都相当大，模型几何比尺λl很难像单项泄水建筑物那样选得小，例如λl≥100的施工导流整体模型是常见的。

（2）由于枢纽中常包括不同的过水建筑物，过水断面尺寸和过水能力往往差异很大，而他们既可能联合运行（如汛期泄洪时）也可能各自单独运行，因而对模型试验来说流量变幅很大，模型尺寸要做到最小放水流量情况下的水深和流速仍满足基本相似条件和观测需要，这又使得λl不能太大。

（3）由于模型中有挡水、泄水、输水等建筑物，河床内可能洲滩罗列，河岸弯曲凹凸，以及导流墙、引航堤等建筑物形态引起的环流、涡旋等局部水流结构，模型在几何变态情况下也不可能与原型完全相似。因而保证几何相似和重力相似是十分重要的；同时模型从上游到下游还有相当长的一个河段，故也须做到沿程阻力相似。这就决定了必须在正态的前提下设计模型。

根据以上所述：水利枢纽施工导流模型应设计成满足重力相似条件和阻力相似条件的正态几何相似模型。

但施工导流动床模拟，特别是分期导流动床模拟有其自身的特点及难点，主要表现在以下几个方面：

（1）冲刷类型多样化。水利水电枢纽在施工导流过程中，建筑物及基础受到的冲刷归纳起来有以下几种：①河床束窄后沿围堰坡脚的冲刷；②纵向围堰与上、下游横向围堰连接处的冲刷；③导流缺口及下部底孔联合泄流时泄水渠段的冲刷；④水跃或二次水跃、非悬空的跌流或二次水跃的冲刷；⑤平顺水流、带局部漩滚及回流的冲刷；⑥其他如立轴、斜轴漩涡的冲刷等。

（2）河床地质条件复杂。水利水电枢纽河床覆盖层地质条件一般较复杂，覆盖层深厚，每层之间的连接面一般也呈不规则曲面，每层颗粒大小差别很大。对每一层而言，是取一个代表粒径（中值粒径）还是两个代表粒径，或者是针对颗粒组成不取代表粒径，而是选出一个较满意的比尺，对所有各组土粒进行模型沙的缩制，就成了施工导流动床模型沙模拟的一个难题。

此外跨海桥梁在建设过程中多借助围堰来进行承台施工，围堰作为一种大尺度结构物，必然会对周围水流产生较大的扰动作用，进而导致其周围产生局部冲刷现象，而围堰周围的局部冲刷可能会使围堰本身发生倾斜，围堰周围海床的冲刷也会对桥梁基础及地基承载力构成威胁。段伦良［9］为研究跨海桥梁施工过程中围堰周围海床的局部冲刷深度与冲刷坑形态，研究了哑铃型围堰周围的流场特征及吃水深度、流速对围堰周围海床局部冲刷深度的影响。刘聪聪［11］以某大桥深水基础为研究对象，量化分析河床有无预开挖条件下，围堰及上游桩基水流、泥沙运动规律。以上研究均基于数值模拟模型基础，对清水条件下物理模型试验的相关研究较少。

同时，针对河床沙粒径及级配选择，钟德钰［6］采用数值计算方法，描述了床沙级配变化的动力学方程和床沙级配在交换层内垂向变化与水流强度、河床冲刷强度的关系，反映了冲刷过程中交换层内向床面补充的物理过程，可用于沙质河床冲刷粗化模拟。李林林［10］运用概率分析法得到了基于起动概率的清水冲刷后河床粗化层级配的计算方法，可为天然河流中沙质河床或卵石夹沙河床粗化机理研究提供依据。

因此针对围堰运用的具体情况，要采用合适的流速计算公式以及合适的泥沙比尺，正确选择河床沙粒径比尺和级配，才有可能正确地模拟工程的实际冲刷状态。

1 底沙动床模型设计基本原理

所谓清水底沙动床模型则指的是不考虑上游来水携带泥沙而建筑物枢纽附近按覆盖层颗粒级配模拟成活动河床的模型［5，7，9，10］。

1.1 水流运动相似

泥沙运动相似的前提是水流本身相似［3，5］。水流相似理论概括说来有下述主要条件：

（1）满足边界条件相似和几何相仿，或各向几何尺度比尺一定；

（2）满足流态相似，通常这意味着模型应有足够大的水流雷诺数，使模型流态与原型流态同属于紊流阻力平方区。显然这一条件控制着模型水深比尺的选择；

（3）满足惯性力（包括弯道产生的离心惯性力）与重力比的相似（弗劳德准则）；

（4）满足沿程阻力与重力比的相似。

（5）如要流速分布相似，则要求模型为正态几何相似模型。

1.2 底沙运动相似

对于研究底沙冲淤问题的模型来说，底沙运动相似主要是启动流速相似［2，3，8］，即：

式中：λv为流速比尺；λvk为起动流速比尺。

式（1）在模型设计中的重要性在于一定水深下起动流速vk完全决定于床沙本身的物理力学性质，因而是选择模型床沙的主要根据。同时该式在河床演变方面的重要性在于可以保证冲刷部位的相似。因为以几何相似和水流相似为前提的模型，如能满足这个条件，就意味着原型某处水深和流速能使该处泥沙启动，模型相应处相应的水深和流速也能使相应位置的泥沙启动。

根据雅林（M S Yalin）、希尔兹（A Shields）及罗斯（H Rouse）等人对泥沙起动规律的研究，如果原型沙粒径足够大（例如原型沙为卵石），模型场地及水流条件也不受限制，采用与原型沙同比重的天然沙做模型沙，且由原型沙粒径按几何比尺缩小求得模型沙粒径，就能设计出这种几何相似的、理想的正态模型。

如果使用天然沙，按模型沙比尺与水深比尺相等求得模型沙过细时，改用轻质沙也可以解决泥沙起动相似问题。当然以此为标准选择的模型沙，未必能满足阻力相似要求，对于较长河段的河工模型，如果原型河床糙率较小的话，则可以采用长度比尺大于深度比尺的变态模型。如果在模型比尺和模型沙选择上还有困难，则可考虑采用系列模型，模型沙采用原型沙、非原型天然沙和塑料轻质沙等［6，9，11］。

因此，对于底沙动床模型，控制模型沙选择的主要条件就是起动流速相似条件式（1）。但具体应用此条件时必须知道起动流速与沙粒物理力学性质（容重γs、粒径d等）的关系，才能对各种可能材料（即各种γs）定出正确的粒径比尺，并在选定材料和粒径比尺后，由原型沙粒径级配决定模型沙粒径级配。

2 施工导流清水动床冲刷模拟相似性及模型沙的选配

2.1 围堰束窄河床段的河底动水压力及水深的函数表达式

导流模型试验的主要目的是检验分期导流河床束窄后的围堰堰脚冲刷情况，以便提供坡脚保护措施。因此冲刷计算必须选择与河床束窄后的围堰堰脚冲刷类型相对应的计算公式。

围堰束窄河床段的河底动水压力及水深的函数表达式可用式（2）和（3）表示［1］：

动水压强的函数关系式：

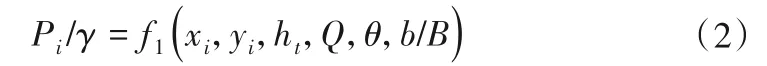
水深的函数关系式：

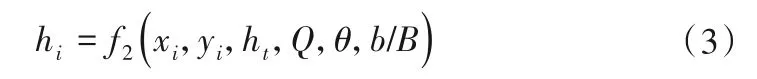
式中：Pi/γ、hi为任意点i处河床底部动水压力及水深；xi、yi为任意点在围堰上游纵横围堰相交的转角处的各点横、纵坐标；ht为下游天然河道水深；Q为围堰束窄河床处流量；θ为纵、横围堰之间的夹角；b、B为河床束窄后的剩余河床宽度与原河床过水宽度。

上述函数的显式可表达成下列两个无量纲数：

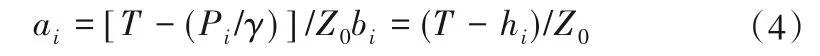
式中：ai，bi为相对动水压差及相对自由水面降落；Z0为计及行近流速在内的上游壅水高度。为围堰上游断面动能修正系数；V0为围堰上游断面平均流速。

以上符号如图1所示。

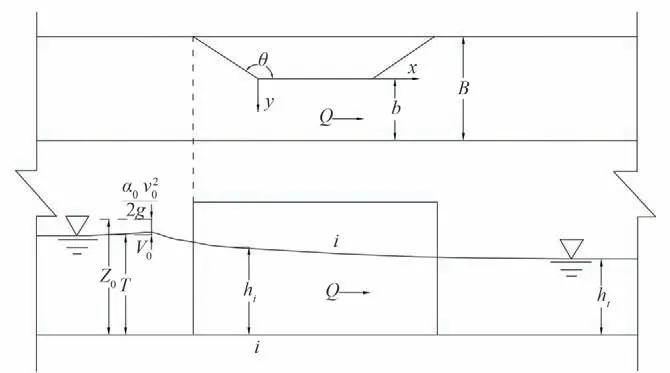
图1 围堰束窄河床段示意图Fig.1 Sketch of narrow riverbed section near the cofferdam

2.2 河床束窄段（特别是围堰转角附近河床）近底流速计算

根据2.1的论述，可写出河床底部流速的能量方程为：

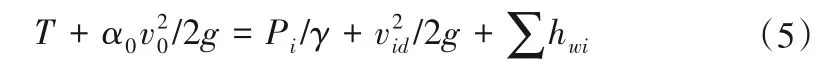
对于表面流速同样可写出下式：

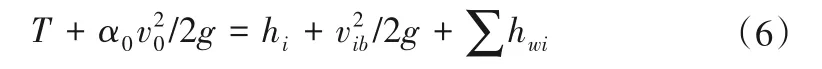
式中：vid、vib为i－i断面的底速与表速。

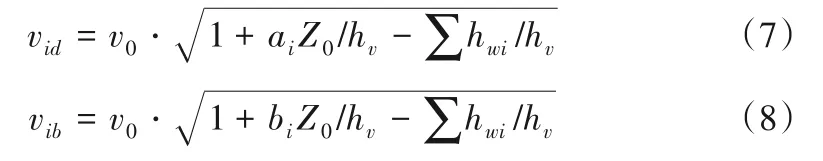
式中：ai、bi、Z0见式（4）。

忽略较小的相对损失∑hwi/hv后，可得：

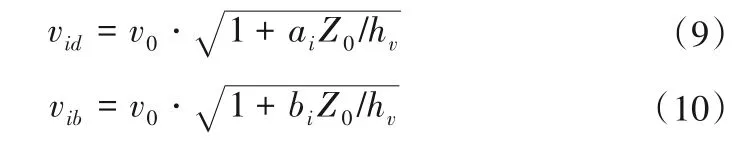
由上得知，围堰转角附近的最大近底流速可按下式确定：

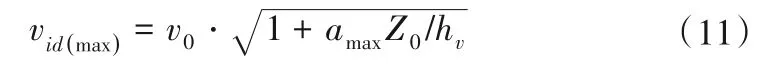
式中与转角θ对应的amax见表1。

表1 与转角θ对应的amaxTab.1 amaxcorresponding with θ

2.3 清水动床模型相似性及比尺选择

因模型试验的任务是研究清水动床（以推移质为主）下的分期导流围堰冲刷问题，故不考虑沙的悬浮相似问题。

（1）起动流速相似。根据1.2 的论述，底沙运动相似需满足的相似条件为式（1），即：λv=λvk

一期导流时，因要查明围堰束窄区的冲刷情况，根据上述2.1 及2.2 的推导，采用围堰转角附近的最大近底流速作为泥沙起动流速公式，即：

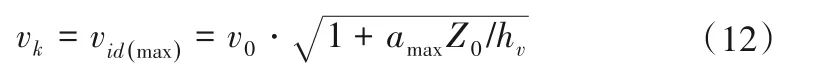
据上述泥沙起动流速公式，即可推出起动流速比尺关系满足λv=λvk。

（2）河床变形相似及比尺。对分期导流围堰冲刷模型试验而言即为局部冲刷相似。

根据国内最常用的局部冲刷式［7，12］：

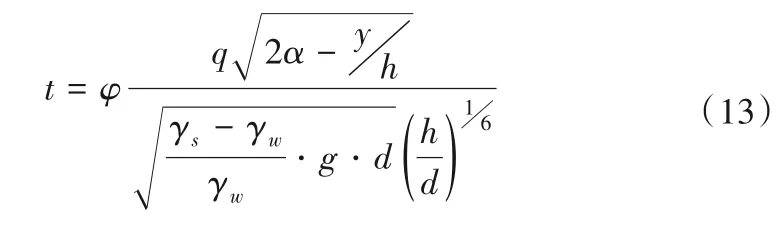
式中：t为冲坑在水面以下的深度；h为进入冲坑前的水深；q为单宽流量；y为垂线流速分布的最大值距底面的高度；α为流速分布不匀的动能修正系数，约为1.0～1.5；d为动床沙粒径（一般取代表粒径）；γs、γw为动床沙与水的密度；g为重力加速度；φ为常数。

对于正态模型，因：

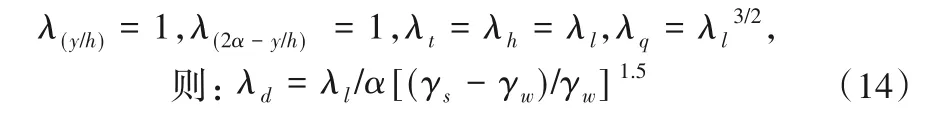
根据2.1 的论述及处理，选择公式（13）作为局部冲坑的计算公式，并综合考虑式（11）和式（14）选择λd的比尺与粒径。

（3）模型沙与原型沙的容重及孔隙率的校正。模型沙与原型沙的容重可以做到相同或近似相等。孔隙率不相等是常见的，根据原型和模型沙孔隙率的差异，应作适当修正。

3 工程实例

3.1 工程概况

向家坝水电站位于金沙江下游河段，是金沙江梯级开发的最后一级电站。根据向家坝坝址的地形、河道水文和水工枢纽布置特性等因素，工程施工导流方式采用分期导流。一期先围左岸，由右侧束窄后的主河床泄流，在一期基坑的左岸非泄流坝段内设置5 个10 m×14 m 导流底孔及缺口；二期主河床截流，由左岸5 个导流底孔及上部缺口联合泄流；后期左岸缺口加高后，由5 个导流底孔、临时船闸和泄水坝段的10 个永久中孔泄流。

3.2 施工导流动床模拟的难点

本试验在一期导流时研究束窄河床的泄流能力以及围堰坡脚采用铅丝笼等保护措施的可靠性。

向家坝水电站坝址附近河床覆盖层深厚，约40 m 左右（▽230.00 m～▽270.00 m）。覆盖层中第一、第二层土料颗粒分布性状由表2所示。

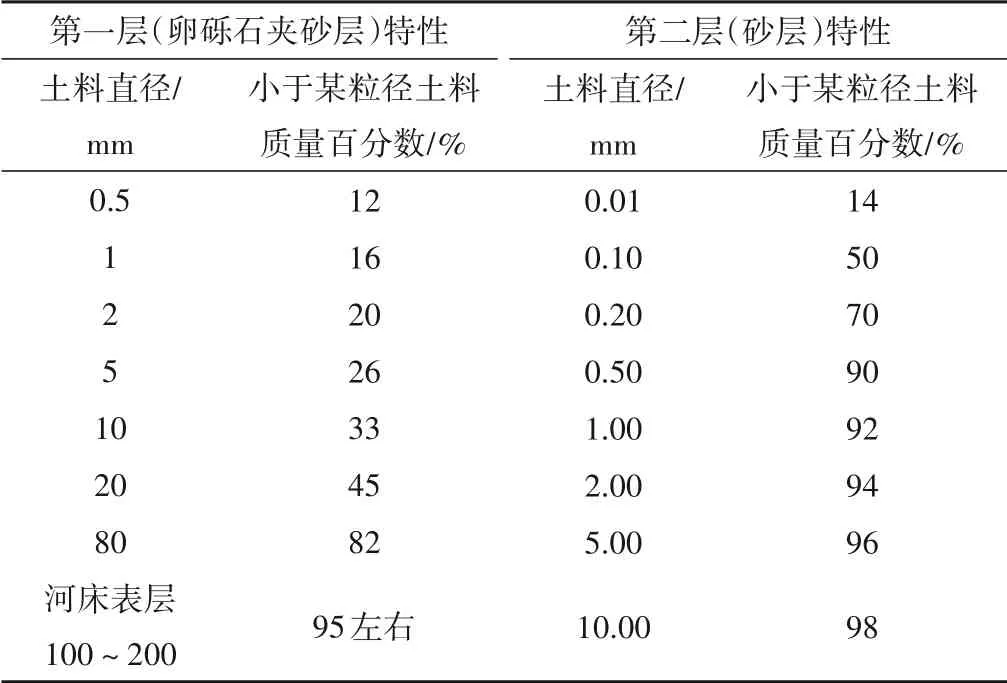
表2 河床覆盖层颗粒分布性状表Tab.2 Particle distribution characteristics of riverbed overburden

导流模型比尺为1∶100，但从上表看出，第一层卵砾石夹砂中，粒径在0.50～5.00 mm 之间的颗粒质量含量达26%，若取最大粒径5 mm计算，则模型沙应为5/100＝0.05 mm。尤其困难的是，第二层中0.01～0.50 mm 的颗粒占90%，若以最大粒径0.50 mm 计算，则模型沙应为0.50/100＝0.005 mm，这样细颗粒的沙就是用塑料沙或精粉煤灰作模型沙也很难实现，所以向家坝水电站导流模型试验的模型沙选择就成了首要难题。

3.3 模型沙比尺选择

对向家坝水电站导流期围堰冲刷问题而言，动床沙的代表粒径很难选择，因为粗细含量都很大，第一层与第二层的颗粒直径差别也太大（相差百倍以上）。如果分层选代表粒径，则第一层最好应选2～3个代表粒径；第二层至少也要选两个代表粒径，这在冲刷坑计算和具体选模型砂时存在很大困难。因此根据2.3 的论述及处理，选择公式（13）作为局部冲坑的计算公式，并选择模型沙比尺与式（14）计算相同。

由式（14）计算可得：

λd≈50

由此可以选择模型沙粒径及颗粒级配组成。设计洪水过程之后一期导流的冲淤数据显示，在一期土石围堰桩号0+700 m～0+1 000 m 之间有冲刷，冲深3～5 m。在桩号0+1 000 m～0+1 500 m 之间有淤积。在桩号0+1 500 m 之后未见明显的冲淤现象发生。并针对冲淤情况进行了相应的围堰坡脚多种保护措施试验。工程采取推荐的保护措施后，实际导流过程中的冲刷实测成果也验证了模型试验选择模型沙比尺的准确性。

4 结论

与河工或单项泄水建筑物的水流模型相比，施工导流模型本身具有一些特点，特别在考虑动床冲刷时，又带来模型沙相似比尺以及粒径选择的问题。通过相似理论的介绍分析，得到了导流模型围堰冲刷清水动床模拟的一些思路：

（1）通过围堰束窄河床段的河底动水压力及水深的分析计算，得到了围堰转角附近的最大近底流速计算公式；

（2）证实了围堰转角附近最大近底流速的计算公式，满足泥沙起动流速相似，从而满足泥沙运动相似；

（3）利用常用的局部冲刷计算公式，考虑到模型的正态要求，得到了泥沙比尺，并建议结合泥沙起动流速相似，进行模型沙的选择。

（4）通过承担的金沙江向家坝一期纵向土石围堰冲刷的清水动床模型试验证实，以上的思路和做法是可行的。□