基于基本块分组与融合的特征直线检测算法
马 瑞,胡立华,左威健,刘爱琴
(太原科技大学 计算机科学与技术学院,山西 太原 030024)
0 引 言
基于图像的特征检测是实现三维重建[1]、图像匹配[2]、物体检测[3]以及遥感图像分析[4]等实际应用的重要步骤之一。基于图像的特征检测主要包括特征点、特征直线和特征区域,相较于特征点和特征区域,特征直线具有特征表达能力强,描述特征几何信息、特征间拓扑关系清晰丰富等优点,成为特征检测的研究热点之一。近年来,基于图像的特征直线检测已广泛应用于SLAM[5]、场景跟踪[6]、无人驾驶[7]以及工业检测[8]等系统中。然而针对场景复杂、结构各异、纹理重复严重的对象,现有特征直线检测方法存在严重的断线以及断线过融合的现象,导致出现完整直线数量较少、错误检测率较高的问题。
针对上述问题,文中结合改进的自适应Canny边缘检测算法[9],提出基本块的概念,设计了一种基于基本块分组、渐进式融合的特征直线检测方法。利用新的Helmholtz原理准则剔除由噪声等外界干扰形成的虚假特征直线,得到准确特征直线集。实验用Matlab 仿真工具进行了验证,结果证明了该算法对特征直线检测的高效性。
1 相关工作
目前,常见的两类特征直线检测方法为:基于图像空间变换域的特征直线检测方法和基于图像像素信息的特征直线检测方法。
基于图像空间变换域的特征直线检测方法是一种全局特征线检测方法,其基本思想是在图像的整体范围内提取特征点,以特征点位置作为驱动数据,设置参数方程将图像中的点映射为参数空间中的点,依据参数空间网格进行投票累计,由此将图像空间中的特征线提取问题转化为参数空间中的极值搜索问题。典型算法有:D.H. Ballard提出的Hough变换(HT)[10],它将图像域中的全局模式检测问题转化为参数空间中的有效峰值检测问题,但是该算法存在复杂的阈值设置问题,对纹理清晰的图像及低对比度区域出现错误检测,且算法计算量大,内存消耗大。因此,近几十年来学者们对HT的缺点进行了仔细的研究并提出许多改进方法。如广义霍夫变换(GHT)[11]、随机霍夫变换(RHT)[12]、数字霍夫变换(DHT)[13]等,这些算法主要集中在提高HT的效率,仅仅提供特征直线的长度和它与轴线的夹角,不提供关于特征直线端点的信息。Matas J等人[14]尝试使用错误检测机制来自动设置检测阈值,然而该方法在实际应用中时间复杂度较高,缺乏可伸缩的终止准则。Atiquzzaman M等人[15]提出了确定一条线的长度和端点的算法,具有高计算性,不适合实时应用。Chao X等人[16]提出了一种基于改进随机霍夫变换的线检测算法,利用像素梯度方向差的概念,计算每个边缘组中相邻像素的梯度方向差。尽管研究者对HT算法做了如此多改进,但基于Hough的方法都有一个共同的缺点,即它们的性能取决于边缘检测的质量,这是因为它们使用的是边缘映射而不是原始图像。
基于图像像素信息的特征直线检测方法是一种局部感知组合法,其基本思想是从图像中提取边缘灰度或梯度等局部信息,利用局部特征的相邻性、延续性等几何关系确定候选直线区域。典型算法有:董晶等人[17]提出边缘主方向和图像梯度方向相结合的算法,该算法结合主元方向和梯度方向信息连接方向相似的边缘,增强了候选直线段的抗干扰性,但是算法参数较多,线段碎片化严重,无法完整检测交叉线特征;戴激光等人[18]提出基于边缘跟踪的算法,但算法计算复杂度较高;Akinlar等人[19]提出基于边缘信息的检测算法(edge drawing lines,EDLines),该算法能够在较短时间内给出比较准确的直线检测结果,但对弱边缘图像特征检测不准确;Lu等人[20]提出一种自适应参数的 Canny算法,该算法直接从图像或包含所有结构信息的边缘图中提取共线点簇进行扩展合并,利用最小二乘拟合方法检测特征直线,但其依赖于边缘检测方法,对噪声敏感;Gioi等人[21]提出一种快速的特征线段检测算法(line segment detector,LSD),该算法通过图像各像素梯度方向进行矩形拟合,利用Helmholtz原理进行验证产生准确线段,并在低水平上控制误检测的数量,具备运行速度快,算法参数能够自适应等一系列显著优点,被看作是现代特征线检测算法的一个标杆;Cho等人[22]提出一种基于线段片(Linelet)算法,该算法在图像数字化后,用一组水平或垂直方向上可连成特征线的像素点集来模拟图像空间中特征线的内在属性,但针对高分辨率图像易产生过分割现象。Almazan 等人[23]提出融合图像域中的感知组合法以及Hough域中的全局积累法的优点来检测特征线,然而易将特征线段分割成多个特征线段;Yang Liu等人[24]在LSD算法的基础上提出基于长度的特征线实时检测器LB-LSD,融合了图像中的梯度信息和结合边缘链接思想进行特征线检测,结果出现过融合现象,错误检测较多。
BPC_GF算法的主要工作有以下几点:(1)目前人工场景中的大多数建筑都具有结构化构造,很容易用直线来勾勒,并且图像中直线结构类似边缘属性,其精度取决于边缘检测的质量,因此文中采用改进的自适应Canny边缘检测算法检测图像边缘点的属性;(2)针对现有的特征直线检测器在场景复杂、纹理重复的图像中易将感知上单一的直线段过分割成多条短线段的缺点,结合贪心算法引入基本块概念,提出了一种基于基本块分组与渐进式融合的特征直线检测方法,从而克服了短线段之间的重叠;(3)针对图像易受噪声、光照、尺度变化等影响在基本块的融合过程中易发生过融合现象,导致特征直线的错误检测率升高,采用了一种新的基于Helmholtz原理的特征直线验证准则,以确定检测出的特征直线的准确性。
2 基本概念
给定灰度图像I,采用改进的自适应Canny算子[9]进行边缘检测后得到n个边缘像素点集P={Pi(Mi,Gi,Xi),i∈[1,n],Mi∈[0,255],Gi∈[0,360]},其中Mi为边缘点Pi的梯度幅值,Gi为边缘点Pi的梯度方向,Xi(xi,yi)为边缘点Pi的几何位置坐标信息。基于边缘信息点集P,给出如下定义:
定义1 瞄点K:在给定边缘像素点集P中,K(MK,GK,XK)为瞄点当且仅当满足如下条件:
(1)
定义2 次瞄点SK:设K为边缘像素点集P的瞄点,K的次瞄点SK(MSK,GSK,XSK)满足如下条件:
(2)
其中,N_8(K)表示瞄点K的八邻域信息。
定义3 搜索方向SD(A,B):给定当前图像I内任一特征边缘点A(MA,GA,(xA,yA))及相邻特征边缘点B(MB,GB,(xB,yB))。如果点B在点A的左右位置时代表横向搜索SDH,上下位置时代表纵向搜索SDV,左下右上位置时代表45°斜向搜索SDS45°,左上右下位置时代表135°斜向搜索SDS135°,则当前边缘点A,B可确定的搜索方向SD(A,B)形式化描述为:
(3)
定义4 基本块C:给定边缘点集P、瞄点K及次瞄点SK,若像素点子集{K,SK,Pi,Pi+1,…,Pi+j}满足如下条件时,则可构成基本块C:
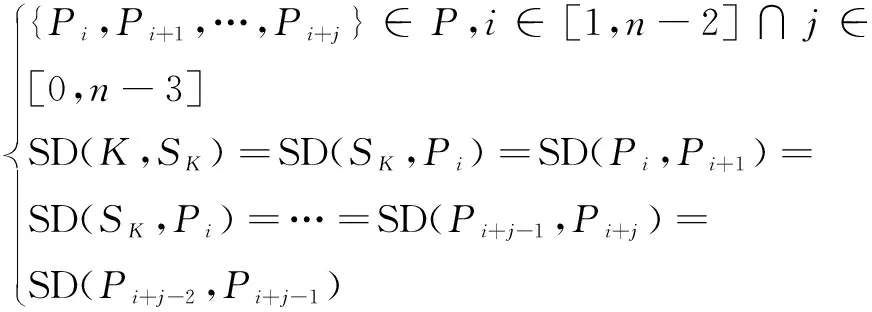
(4)
从定义1、2出发,边缘点集之间依照不同的搜索方向(定义3),如果满足定义4则可构成基本块,由此基本块可划分为:横向基本块H、纵向基本块V、45°斜向的基本块S45、135°斜向的基本块S135。
定义5 基本块C的长度LC:设P1(M1,G1,X1),P2(M2,G2,X2)为基本块C的起始边缘像素点和终止边缘像素点,则基本块C的长度为:
LC=Dist(X1,X2)
(5)
其中,函数Dist()计算基本块C的欧氏距离。
定义6 主方向角θ:给定基本块C,C的主方向角θ可通过下面步骤计算:
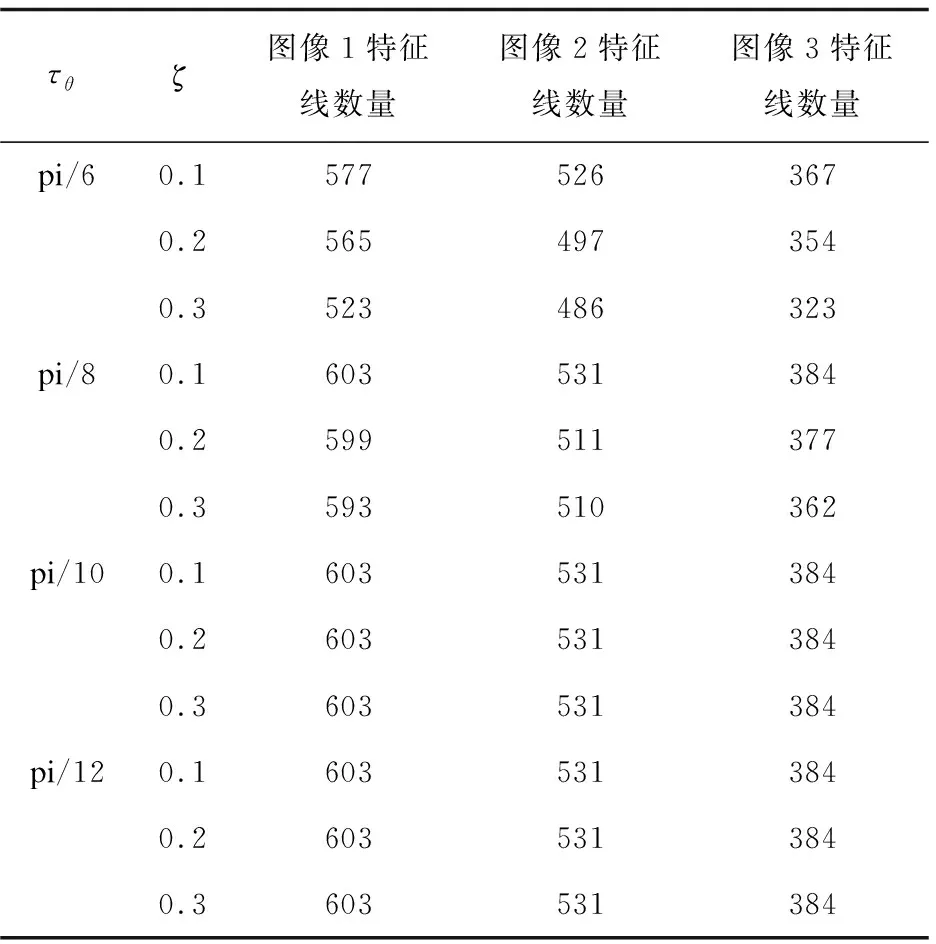
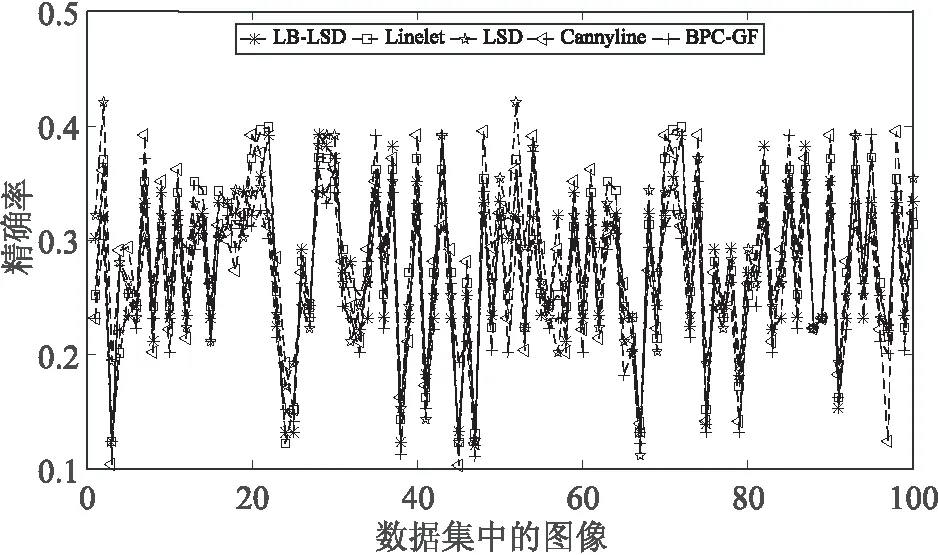
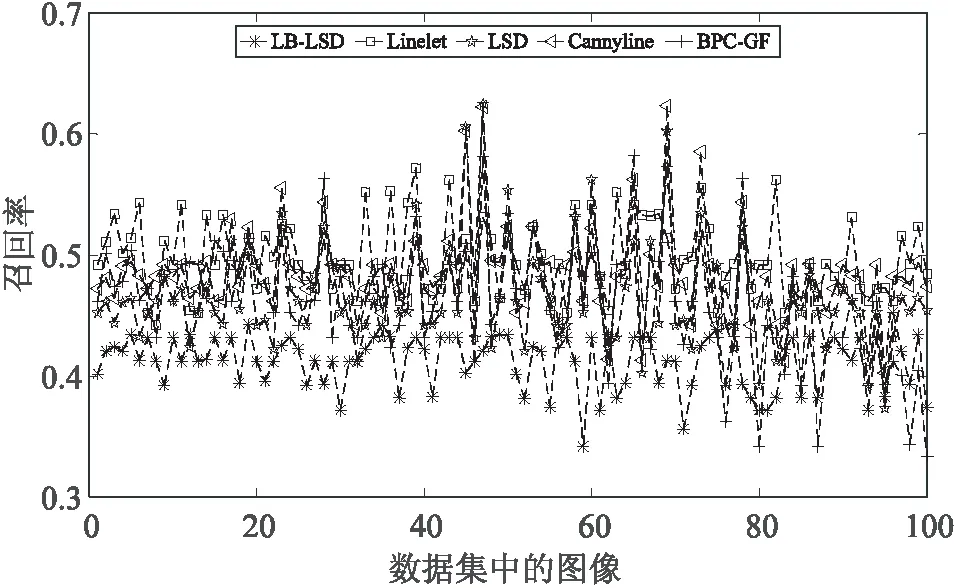
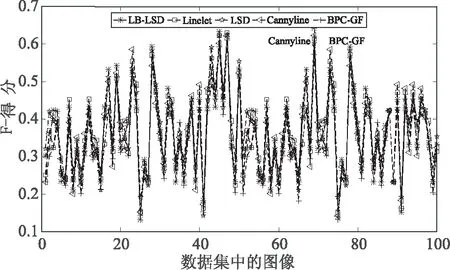
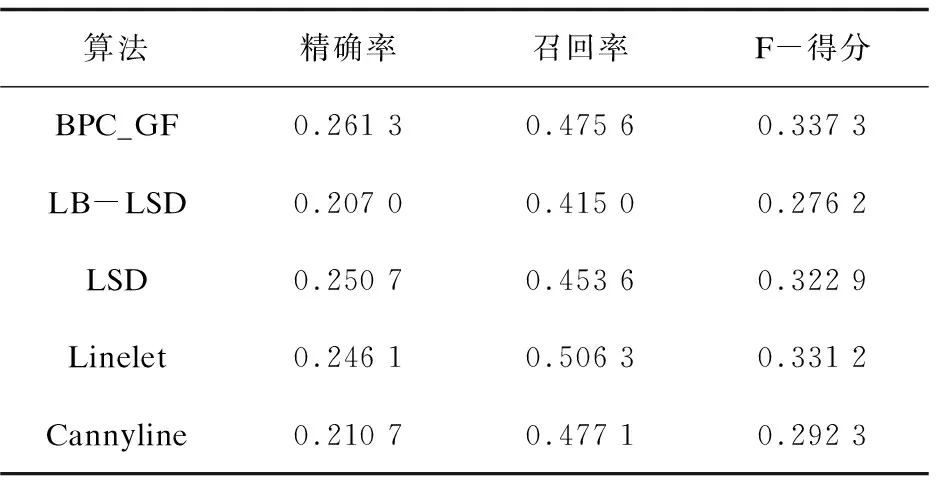
(1)计算C={Pi(Mi,Gi,Xi),0 (6) (2)对基本块C内所有特征边缘点Pi的水平线角求均值即为基本块的主方向角: (7) 定义7 基本块间空间距离S:给定基本块Ci邻域内的同类基本块Cj,Ci、Cj邻近端点的横坐标或纵坐标的偏移量ζ、μ满足0≤ζ≤2或0≤μ≤2时,计算两基本块间的欧氏距离S(Ci,Cj): (8) S(Ci,Cj)=Dist(ci,cj) (9) 其中,Ci,Cj两端边缘像素点坐标分别为(xi1,yi1)、(xi2,yi2)和(xj1,yj1)、(xj2,yj2);ci,cj表示为Ci,Cj邻近端点。 定义8 自适应空间距离标准τs:如果基本块间空间距离S小于τs,则基本块可以进行分组。 τs=ξ·LCi (10) 由于每个基本块的长度是随机的,如果仅用基本块的长度和基本块间空间距离S做比较,其检测结果的误差明显较大,所以引入参数ζ,其取值0<ζ<1。 BPC_GF算法主要分为三个关键步骤:基本块划分、基本块分组融合、错误特征线的剔除。算法的整体设计流程如图1所示。 图1 算法流程 依据每个边缘像素之间梯度、灰度的属性,将同一搜索方向的边缘像素划分成不同类型的基本块,从而进行分组融合,使得特征直线检测更准确。边缘像素划分为基本块的算法流程如下: 算法1:边缘像素划分基本块算法。 输入:灰度图像I 输出:图像I的基本块集C={Ci,Ci∈{H={Hi,0 (1)采用改进的自适应Canny方法获得图像I的边缘点集P={Pi(Mi,Gi,Xi),i∈[1,n],Mi∈[0,255],Gi∈[0,360]} (2)依照边缘点的幅值信息对所有边缘点集进行降序排序 (3)初始化基本块C=Φ (4)For eachPi∈Pdo (5)Find the pointsK(由定义1确定) andSK(由定义2确定) in thePaccording to definitions 1 and 2 (6)According toKandSKCompute the direction of search SDi,SD={SDH,SDV,SDS45,SDS135} (7)AddKandSKtoCi,Ci∈{H={Hi,0 (8)WhilePi∈N_8(SK) and satisfy SD(Pi,SK)∈SD(SK,K) do (9)AddPitoCi (10)K=SK (11)SK=Pi (12) end while (13) if length(Ci)≥ 3, then (14)C=C∪Ci (15) End if (16) Delete edge pixel in theC,updateP (17)End for 经过3.1过程后图像中的边缘像素点被合理分配到不同基本块中,基于单个基本块长度较短,因此,依据相邻基本块间主方向角相近且空间距离较小的特点,将满足以下两个约束条件的同类型基本块进行分组融合。 (1)基本块间的空间距离(定义7)满足一定的自适应空间距离标准τs(定义8); (2)基本块间的主方向角(定义6)之差Δθ满足一定的自适应空间角度标准τθ。 以横向基本块集为例,基本块分组融合算法基本流程如下: 算法2:基本块分组融合算法。 输入:横向基本块集H={Hi,0 输出:图像中的特征线及特征线的条数num (1)计算H中基本块的长度L,并进行降序排序 (2)计算H中基本块的主方向角θ (3)初始化线段集合:D=H,GroupG=Φ (4)forD1∈Ddo (5)L1=MAXlength(D1) (6) For eachDi∈D-1 do (7)Ifθ(Di)-θ(D1)<τθthen (8)G=G∪Di (9)End if (10)End for (11)P=Φ (12)For eachGi∈Gdo (13) IfS(Gi,D1)<τsthen (14)P=P∪Gi (15) End if (16)End for (17)R=Φ (18)ForD2∈Pdo (19)M=MergeTwoLines(D1,D2) (20) IfM≠Φthen (21)D1=M (22)R=R∪D2 (23)End if (24) End for (25)D=DR (26)End for 同理,检测其余三类基本块中的特征直线。 在对基本块进行划分时,由于边缘检测得到边缘像素的密集区域容易对基本块产生错误判断,而边缘像素稀疏区域由于噪声影响导致基本块错误分布,从而影响特征直线检测,因此为使检测到的特征直线更精确,对检测结果进行验证已成为直线检测算法的重要步骤之一。常用于验证所检测直线的准确性的方法为Helmholtz原理,如:LSD、cannyline及EDline。 在LSD检测算法中,建立了抑制虚假线段出现的数学模型,模型假设梯度方向是独立的,并且在图像中均匀分布,与“零假设”的显著偏差具有相关性,并揭示了线段的存在,因此该方法是一种反向准则。在含有特征线的情况下,考虑噪声模型中的虚警特征直线具有与所观测的真实特征直线一样多或更多对齐边缘点的事件。如果随机期望很小,则感知上是有意义的。定义一个“虚假警报的数”(number of false alarms,NFA)即: NFA(s,p)=γNLB(|s|,ks,p) (11) (12) 其中,s是图像中检测到的特征直线,|s|是s的矩形拟合区域,ks是矩形内与特征线方向对齐的像素点,p是随机像素q具有相同方向的概率,NL是图像中可能的特征直线数,γ是归一化值,B(|s|,ks,p)是二项分布。 LSD算法中的验证步骤只查找了与拟合矩形的主方向轴完全对齐的像素点,为了克服检测出的直线的碎片化,Yohann Salaün等人[25]将验证公式进行推广,以LSD算法中短线段S={s1,s2,…,sn}为基准进行融合验证。 BPC_GF中图像中检测到的特征直线是由多个空间距离相近,主方向角相似的基本块融合而成的直线。因此,通过检测构成一条特征直线的每个基本块的NFA与该特征直线的NFA进行比较来判断该特征直线是否检测正确。假设一幅图像大小为M*N,则定义一条特征直线的NFA为: 1)B(|Ci|,kCi,p) (13) 其中,m是基本块融合后的特征直线,MN5/2是图像中可能的特征直线数目,n是检测到的特征直线中的基本块数。 为了计算特征直线中各个基本块的NFA,可采用LSD中使用的相同背景和对象模型,其表达式同LSD。 (14) 通过上式计算如果F<0,则认为分组融合后的特征直线是有意义的。 算法实验的环境为:Windows 10操作系统,2.3 GHz Intel(R) Core(TM) i5处理器,4 GB内存;山西太原晋祠图像采集工具参数为像素1 200万的三星智能手机,中国科学院自动化研究所模式识别国家重点实验室提供的三维重建数据集[26]采集设备为佳能EOS 5D,采集图像像素为4 368*2 912。基于上述环境,采用Matlab编程语言,以山西晋祠和中科院三维重建数据集为对象,实现了基本块检测分组、渐进式融合、特征验证的直线检测算法。文中的对比实验的源代码可以在网上公开获取。其中实验操作时首先需对采集图像进行预处理,处理后的图像像素为640*480。 BPC_GF算法涉及到的关键参数分别为:Canny边缘检测时的高斯滤波参数δ,高阈值τh,低阈值τl,主方向角偏差阈值τθ与空间距离阈值τs,系数ζ,其中δ,τh,τl默认使用改进的自适应Canny边缘检测算法[9]中的参数,τθ进行自定义,τs根据基本块的长度和ζ而定,ζ是用来计算距离偏差的系数,检测结果最终采用图像中检测到的特征线数量进行判断。为了验证参数值对图像特征线检测的影响,在数据集上随机选取三幅古建筑图像进行检测,表1表示参数τθ与ζ的选取对图像特征线检测结果的影响。 表1 τθ与ζ取值对直线结果的影响 从表1中可以看出,当参数设置为τθ>pi/8,ζ>0.1时,算法检测效果逐渐变差,当参数设置为τθ<=pi/8,ζ>=0.1时,算法检测结果基本保持稳定变化。由表1可知,当τθ=pi/10、ζ=0.1时图像中检测到的直线不再受参数取值的影响,且检测到的特征直线最多,因此,将τθ=pi/10、ζ=0.1作为BPC_GF算法实验的参数设置。 为了更加清楚地说明BPC_GF算法检测的特征直线性能,记TP(true positive)为真正例,即正确检测到的特征线的数量,FP(false positive)为假正例,即错误检测到的特征线的数量;FN(false negative)为假反例,即漏检的特征线的数量,然后通过以下3个评价指标对算法进行客观定量的评估。 (1)精确率(precision),表示在检测到的所有特征直线中检测正确的特征直线所占的比例,计算公式如下所示: (15) (2)召回率(recall),表示在检测到的所有特征线中检测正确的特征线所占人工标注图像中的比例,计算公式如下所示: (16) (3)F-得分(F-score),表示精确率和召回率的调和平均数,计算公式如下所示: (17) 其中,β为精确率和召回率的比值,BPC_GF算法认为精确率和召回率同样重要,因此设β=1。采用不同算法即LB-LSD、LSD、Linelet、Cannylines和BPC_GF对图像数据集上随机选取的100幅古建筑图像进行实验,其精确度、召回率、F-得分如图2所示。与其他方法相比,BPC_GF方法具有更高的检测性能。不同算法的平均量化评测结果如表2所示。 (a)精确度 (b)召回率 (c)F-得分 表2 不同算法在所给数据集上的量化评测结果 由此可得出,BPC_GF算法在特征直线检测的精确率方面明显优于现有的算法;在召回率方面,Linelet算法的效果最好,主要原因在于Linelet算法是基于图像中像素局部特征来进行特征线检测。根据实验,以像素的梯度导向为指导对像素进行划分的特征直线检测有利于特征直线召回率检测。BPC_GF算法在边缘检测基础上对像素进行基本块划分,综合考虑算法在精确率和召回率两个方面的性能,BPC_GF算法均取得了较好的结果。 对图像在不同算法检测情况下的时间复杂度进行分析,如图3所示。从图中可以看出,对于同一幅图像,BPC_GF算法的时间最短,相较于最新的LB-LSD算法,BPC_GF算法的时间性能提高了约20%。 图3 在同一图像上不同算法检测所用时间比较 为进一步验证BPC_GF算法的性能,在古建筑数据集上随机选取三幅灰度图像进行不同算法的检测,不同算法上的特征检测结果如图4所示。 图4 数据库中不同图像在不同算法上的检测结果 从检测的结果中可以看出,LB-LSD算法检测的线段长度长,但是检测数量少,检测错误率较高;LSD、Linelet算法检测的线段数量较多,但是线段的碎片化比较严重,导致将感知上单一线段在交点处分割成多个短线段;Cannylines 算法没有克服图像的宽像素边缘;BPC_GF算法精准地检测到的图像中的线段,能够很好地呈现图像的轮廓。 针对场景复杂纹理重复的图像直线提取中存在断线、误检的问题,提出了BPC_GF算法,算法具有以下优点:(1)利用改进的自适应Canny边缘检测算法提取图像边缘点,提高了边缘检测的质量,为特征直线检测奠定了基础;(2)提出对边缘像素点进行基本块划分,分组融合,克服了短线段之间的重叠检测;(3)提出新的基于Helmholtz原理的特征直线验证准则,提高了特征直线检测的效率。经仿真实验和实际应用分析,BPC_GF算法检测效率更高。3 算法思想及其流程
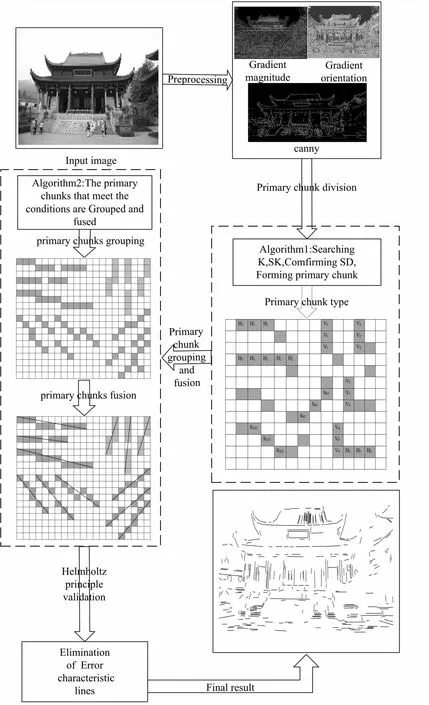
3.1 基本块划分
3.2 基本块分组融合
3.3 Helmholtz原理准则验证
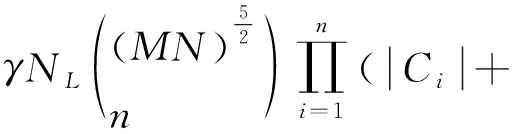
4 实验结果与分析
4.1 算法参数分析
4.2 算法量化分析
4.3 算法时间分析

4.4 算法效果对比

5 结束语

