孔洞对裂纹尖端应力强度因子影响的仿真分析

杨露露，陈 浩，杨亚莉

（上海工程技术大学机械与汽车工程学院，上海 201600）

0 引言

科技的发展驱动材料轻量化。铝合金由于低密度、高强度、低成本的优秀性能，广泛应用于汽车、航天等机械制造行业中。铸造铝合金由于其良好的性能，通常应用于发动机、车架等高强度受力部位，而材料的内部裂纹和孔洞缺陷往往会对铝合金强度造成较大影响［1-2］，因此对铝合金的力学强度研究十分重要，ABAQUS 等仿真分析软件为研究提供了平台支撑。

许多学者对孔洞和裂纹缺陷进行了研究。姜文等［3］、曾祥太［4］从孔洞缺陷的特征出发，展示了孔洞缺陷的特征参数对裂纹的产生和扩展作用，提出了孔洞疲劳寿命的定量预测模型；莫得锋等［5］研究了寿命模型与线弹性断裂模型之间的内在联系，指出在材料缺陷中孔洞的分布往往呈现无规律状态；马迎松［6］研究了随机分布的孔洞对材料的破坏规律。在材料破坏过程中，会经历孔洞成型、裂纹成型到裂纹扩展几个阶段，裂纹和孔洞往往与材料的失效断裂阶段同时存在。在裂纹扩展阶段，孔洞同样会对裂纹扩展产生影响。一些学者研究了残余应力对孔洞裂纹的扩展影响，引入了塑性变形参数，提出疲劳裂纹萌生寿命预测曲线［7-8］。孔洞会改变裂纹尖端的应力分布，从而改变裂纹扩展速率和扩展角度。吕斐等［9］、石路杨等［10］引入应力影响系数来预测裂纹扩展路径的变化趋势；刘剑等［11］、涂文锋等［12］、寇佩佩［13］使用扩展有限元方法对含孔洞裂纹扩展进行分析，证明了扩展有限元的合理性和简洁性；Lang等［14］通过数值模拟和计算，研究了降低裂纹扩展速率的应力分布。ABAQUS 不仅针对材料损伤，在工程中应用也很广泛［15-18］，在机械车辆的动力特性以及强度刚度方面发挥着重要作用。以上研究都是基于各类有限元软件对单孔洞或孔洞裂纹的相互作用来进行，对于三维裂纹尖端受孔洞影响的定量分析研究却较少。本文通过ABAQUS 对含孔洞的6061 铝合金内部的三维裂纹尖端进行特征分析，设定分布参数（距离、大小、角度），研究裂纹尖端的应力强度因子变化，并且通过MATLAB 进行三维拟合，为裂纹扩展速率和角度的变化提供理论支撑［19］。

1 有限元模型建立及孔洞各参数模型分析

三维裂纹和孔洞仿真模型选择长度为a=5mm，宽度和厚度均为b=2mm 的长方体模型，在裂纹设置上选择中间贯穿裂纹，长度为L=2mm，孔洞位置在裂纹尖端中间处，裂纹和孔洞位置二维展示如图1 所示。

Fig.1 Two-dimensional model of hole crack图1 孔洞裂纹二维模型

材料参数设置为：弹性模量E=71 000Gpa，泊松比λ=0.33，模型采用下端固定，上端施加σ=1 000Mpa 的竖直应力，内部贯穿裂纹长度为L=2mm。

由于要研究孔洞对于裂纹尖端处的应力强度因子影响，因此要考虑孔洞的3 种变量参数，分别为孔洞离裂纹尖端的距离l、角度ω以及孔洞半径大小r。由于计算过程中J积分的稳定性，同时对于I 型裂纹，其J 积分和应力强度因子K 之间存在如下关系：

其中E 为材料的弹性模量，因此在计算中采用J 积分进行计算。

ABAQUS 中模型的网格划分为四面体和六面体单元，基于对模型结果要求的精确性，选择六面体网格，全局种子设置为0.04。由于含裂纹孔洞模型无法直接划分六面体，因此需要对其进行切分。将孔洞独立切割出来，再将其均等切割成八等份，并将其由圆心到圆边逐渐加密Sin⁃gle 单元，最小到最大尺寸为0.001～0.002 5，其种子设置如图2 所示。

Fig.2 Local encryption of hole unit图2 孔洞单元的局部加密

最终得到模型的各参数设置如图3 所示。

Fig.3 Model parameter setting图3 模型参数设置

1.1 孔洞距裂纹尖端的距离对J 积分的影响

对孔洞参数进行设定时，由于孔洞离裂纹尖端太远，应力影响会不明显，太近时网格划分又比较困难。因此，对距离l划分为7 组，分别为0.03mm、0.05mm、0.1mm、0.15mm、0.2mm、0.25mm、0.3mm。控制恒定变量为：角度ω=90°，孔洞大小半径r=0.004mm。在进行分析前，对比实验设定为无孔洞时的裂纹中间节点的J 积分，在ABAQUS 后处理模块中可以得出其大小为91.68，将其设为标准值J0。再对7 组含孔洞模型分别分析其节点处J 积分，结果如图4所示的应力云图。

Fig.4 Stress nephogram of result analysis图4 结果分析应力云图

计算差值如表1 所示。

Table 1 The value of J integral varying with hole distance at crack intermediate node表1 裂纹中间节点处随孔洞距离变化的J 积分的值

将其在MATLAB 中进行曲线拟合如图5 所示。

Fig.5 The relationship curve of J integral value changing with hole crack distance图5 J 积分变化值随孔洞裂纹距离变化的关系曲线

从图5 可以看出其函数类型为幂函数，其J 积分差值f(x)的函数表达式为：

对其R2，检验其值为R2=0.996 6，符合拟合标准。

由图5 可以看出，孔洞位于裂纹上方时，孔洞距离裂纹尖端越近，裂纹尖端的J 积分越小，且呈现幂函数形式的变化趋势。孔洞处应力集中，会对其周围的应力场产生弱化影响，这一过程原理近似于工程应用中“止裂孔”的作用。

1.2 孔洞距裂纹尖端的角度对J 积分的影响

模型的设定中力的施加为竖直力，孔洞周围的应力场会随着孔洞和裂纹尖端的相对位置变化而变化。在角度分析中，由于对称性，将孔洞与裂纹中点处的夹角设定为0°～180°即可，本文选择夹角为0°、30°、60°、90°、120°、150°六个角度，控制恒定变量为孔洞到裂纹尖端距离0.1mm，孔洞大小半径为r=0.004mm，对六组模型分析其裂纹中点处J积分结果如表2 所示。

将其在MATLAB 中进行曲线拟合如图6 所示。

在曲线拟合中，对不同函数的R2进行比较，最终确定复合三角函数的函数关系式如下：

由图6 的曲线可知，角度对于裂纹尖端的J 积分有着较大影响，在靠近裂纹尖端水平处的孔洞会增大裂纹尖端的J 积分值，在45°和135°附近时，孔洞对于裂纹尖端的J 积分减小作用最明显，在0°～90°以及90°～180°处的影响近乎相同。

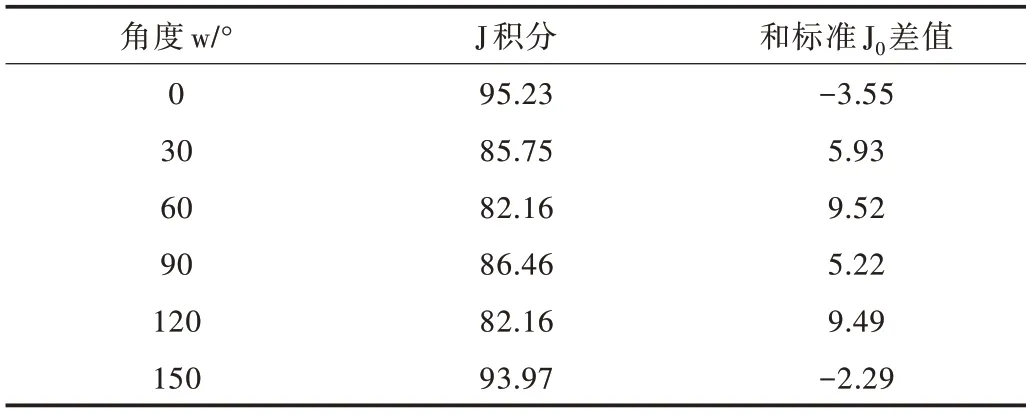
Table 2 J integral value of crack intermediate node varying with hole angle表2 裂纹中间节点处随孔洞角度变化的J 积分值

Fig.6 Relationship curve of J integral ralue changing with hole crack angle图6 J 积分变化值随孔洞裂纹角度变化的关系曲线

1.3 孔洞半径大小对J 积分的影响

在不考虑铸造缺陷的状况下，孔洞往往呈现很小的半径范围，多为微米级别，将其分组设置为1～6μm，其对裂纹尖端中点处的J 积分影响如表3 所示。

Table 3 J integral value of crack intermediate node varying with hole radius表3 裂纹中间节点处随孔洞半径变化的J 积分值

曲线展示如图7 所示。

Fig.7 Variation curve of J integral difference at crack tip with hole radius图7 裂纹尖端J 积分差值随孔洞半径变化曲线

由图7 可知，当孔洞半径很小时，孔洞半径的变化对于裂纹尖端的J 积分影响不明显。有些学者提出孔洞半径大小在25μm［20］时会对材料寿命产生较大影响，此即为孔洞关键尺寸，这与所得结论对应。

1.4 曲线的力学分析验证

分析中间含圆孔平板的应力，根据复变函数理论，圆孔水平和竖直应力分量表达式如下：

利用复变函数理论的保角变换原理，把一个不规则分段光滑的曲线变换到单位圆上，导出复变函数的应力表达式及其边界条件。对任意圆形孔其映射函数的一般表达式为：

可以得到各应力分量的表达式如下：

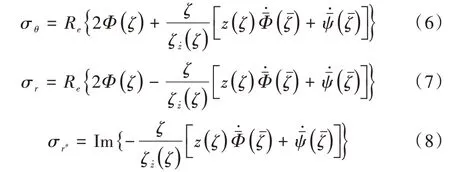
将其单位圆受力展示在图8 中。

Fig.8 Circumferential stress distribution of holes under tensile stress图8 拉应力作用下孔洞周向应力分布

由图8 可知，孔洞周边应力分布随长度（距离）和角度变化趋势和仿真中的曲线基本吻合，证明了仿真数据的合理性。

1.5 孔洞各参数综合分析

通过以上分析可以看出，在微孔洞状态下，孔洞对裂纹尖端的应力强度影响因子主要在于孔洞到裂纹尖端的距离和角度。在MATLAB 中进行拟合程序的编辑运行，分别在程序中编辑距离l和角度w以及裂纹尖端J 积分的变化值，并采用二次多项式拟合曲面，其拟合结果如图9 所示。

确定公式参数，得到拟合曲面为：

其中，x1、x2分别表示距离l和角度，w、y为有孔洞时裂纹尖端的J 积分和无孔洞时裂纹尖端J0的标准差，即J=J0+y。

Fig.9 Quadratic polynomial fitting surface of multi-parameter J integral and standard difference J0图9 多参数J 积分和标准J0 差值的二次多项式拟合曲面

2 任意拉应力和裂纹长度下的应力强度因子K 值预测

在已知不同孔洞分布的J 积分变化情况下，对应力强度因子做进一步分析。由三维空间J 积分理论可知，对于I型裂纹，其J 积分和应力强度因子K 之间存在如下关系：

E 为材料的弹性模量。

应力强度因子K 又和裂纹长度存在如下关系：

其中，Y 为形状因子，a 为裂纹长度，由式（10）得，应力强度因子的大小为形状因子、I 型拉应力大小以及裂纹长度所共同决定，对于含孔洞的裂纹尖端会随着孔洞位置的变化而变化，而在应力以及裂纹长度相对固定的情况下，孔洞位置的变化往往对形状因子间接造成影响。由式（10）、（11）得：

由前文拟合公式（9）可知，每个孔洞的分布都有其相对应的形状因子，由式（11）得孔洞裂纹模型的形状因子为：

在此模型中，应力σ=1 000Mpa，a=2mm，并且J 积分和应力平方成正比，和裂纹长度成正比。由式（13）可得任意孔洞分布下的形状因子Y，因此对于任意应力S 和裂纹长度L 下的裂纹尖端J 积分JA有：

由式（14）可知，通过前文拟合的任意孔洞条件下的J积分变化值，可得出任意孔洞分布下的形状因子，再将其特定的形状因子带入推导公式（14），便可得到单孔洞对于三维裂纹尖端的定量影响，从而得出不同孔洞分布以及材料受力情况下的裂纹扩展速率。

3 结语

通过有限元软件ABAQUS 建模分析，得出裂纹尖端处的孔洞分布不同会对其应力强度因子造成不同的影响。孔洞距离裂纹尖端的距离越近，对降低其应力强度因子越明显，这近似于工程应用中“止裂孔”效果。孔洞对裂纹尖端的相对角度变化多数情况下会减小裂纹尖端的应力强度因子，这一影响在45°或者对称的135°时最明显。研究表明，孔洞影响裂纹尖端应力强度因子是通过形状因子来实现的。形状因子和孔洞参数分布相关，并且可以通过公式将其定量表示，确定了形状因子可通过任意裂纹长度和应力大小来确定裂纹尖端的应力强度因子大小。通过理论分析验证了ABAQUS 仿真结果和MATLAB 拟合用于材料力学强度分析的合理性，以及仿真分析软件在工程应用中的可靠性,因此仿真研究可以较为准确地在微观层面上得到裂纹孔洞相互作用的机理，对于疲劳裂纹扩展预测提供了可行方法。本文主要研究了单孔洞和裂纹之间的相互作用，后续对于多孔洞之间的相互耦合还需进一步研究。