“五家共井”问题的图形化、Python和APPInventor解法

王德贵

中国古代数学巨著《九章算术》是张苍、耿寿昌所撰写的一部数学专著。其内容十分丰富，总结了战国、秦、汉时期的数学成就。是当时世界上最简练有效的应用数学，它的出现标志着中国古代数学形成了完整的体系。其中有一道题是“五家共井”问题，原文如下：

五家共井，甲二绠不足，如乙一绠;乙三绠不足，如丙一绠;丙四绠不足，如丁一绠;丁五绠不足，如戊一绠;戊六绠不足，如甲一绠，皆及。

这道题的白话解释是：五家合用一口井，甲家的2根井绳和乙家1根井绳总长为井深;乙家的3根井绳和丙家的1根井绳总长为井深;丙家的4根井绳和丁家1根井绳总长为井深;丁家的5根井绳和戊家1根井绳总长为井深;戊家的6根井绳和甲家1根井绳总长为井深。问：井深、各家井绳各多少？（每家的井绳均等长）

下面我们也来分析一下“五家共井”问题，并用Python、图形化和APPInventor分别求解。

一、创意来源

在教授学生学习Python四级课程时，合用的练习和案例并不多，于是在搜索案例过程中，看到了这个“五家共井”问题，经过研究发现比较适合用Python四级的知识点来解决，现分享出来。

二、设计思路

这是一个不定方程问题。遇到方程最初的想法还是用枚举法，在100范围内运行后，无果。说明最小正整数解，一定比100大，于是擴大范围到300，结果运行很久也没有输出结果，看来运算时间过长了，没有能等到程序运行出结果。

于是想到库函数sympy，它是一个符号计算的Python库。我在文章《阿基米德群牛问题的分析及Python验证》里讲过，这里不再赘述。

通过解方程，得到关系式，从而求出最小正整数解。

在使用Python求解过程中，想试着再用Scratch和APPInventor求解，通过编程，运行，在对比三种代码之后很有启发，下面把求解过程分享给大家。

三、程序设计

（一）Python程序设计

1.枚举法

这是一种最直接的思路，不知道具体结果，那就用枚举法测试（图1）。根据题意，设甲、乙、丙、丁、戊五根绳子分别长a、b、c、d、e，井深2a+b，5个未知数的满足方程2a+b=3b+c=4c+d=5d+e=6e+a，将1到100分别代入进行试算。

由于运行时间较长，运行时将消耗时间打印出来了，此时显示的是运行了a取值1到10的运行时间222秒（图2）。

2.时间复杂度

如果取值范围在100以内，则时间复杂度是10的10次方，按运行时间算，运行了10个a将近4分钟，那运行100个a，需要的时间就大约是40分钟（图3）。

当a的取值在300以内时，运行1个a需要的时间将近30分钟，那300个a就是近150个小时，需要6天多的时间（图4）。

这样长的运行时间程序完全无法实用，必须通过缩减无效运算来优化程序。改为将最短的绳子e作为枚举的主要参数，根据题目分析我们也能提前知道各未知数的大小关系，将d的试算起始数量从1改为从e开始，其他几个未知数以此类推。根据网络搜索答案，我已经知道e的最小正整数解小于100，b小于300。新增了变量bj=1用来判断，当获得答案后立刻跳出循环。等待一段时间能够获得答案（图5）。

运行10个e的时间将近是6分钟，随e值增大，单次运算时间还会缩短。优化后，运行时间大大缩短了，只需25分钟左右，已经获得了一组结果（图6）。

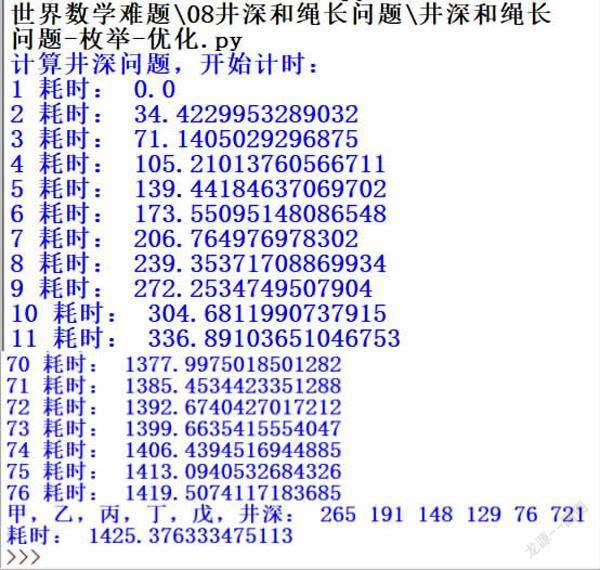
我们根据已有答案回推优化程序，最终获得了结果。但是如果我们不知道答案的范围，即使只在300范围内试算，运行也要6个小时左右。枚举法在面对这样一个不定方程的情况时，如果不知道结果的范围，那么运行时间就会非常长！必须去寻找更简捷的算法。

3.方程解法的程序设计

（1）利用sympy库函数先求出不定方程的关系式（图7）。