“脚手架”如何变成了“绊脚石”

杨南昌　罗毛羽

[摘   要] 小学数学教材和教师的教学过程中提供了大量图文与习题结合的图示，其中大部分本身是作为学生情境支架而设计的，以支撑学生跨越从生活数学到抽象符号数学之间的发展鸿沟。然而，实证调查测试表明，一些数学图示不仅没有起到“脚手架”作用，反而成了干扰学生正确理解题意的障碍。进一步分析发现，这些图示障碍内在的图文匹配度、契合学生的理解度和對学生学习的支持度之间存在正向影响关系;图示内部缺乏一致性、图像内容编排不合理以及图示信息呈现不恰当是形成6种典型图示障碍的三大主因，且通常发生在多媒体学习“选择—组织—整合”词语和画面的不同认知阶段。研究结果为设计和使用数学图示提供了有益启示：遵从多媒体学习的匹配设计、学习者中心的设计和深度学习的情境支架设计三大学习设计原则，不仅可以使图示障碍得到有效控制与消除，也是回归图示本身所赋有的“脚手架”功能的有效途径。

[关键词] 图示障碍; 小学数学; 情境支架/脚手架; 深度学习; 认知分析

[中图分类号] G434            [文献标志码] A

[作者简介] 杨南昌（1974—），男，江西瑞金人。教授，博士，主要从事学习科学与教学设计、课程与教学创新等方面研究。E-mail：south1002@163.com。

一、问题提出

图文并茂是小学教材编写的一大特点。在小学生的数学学习过程中，碰到“图中有题”或“题中有图”的图文混合问题解决更是司空见惯。特别是在小学低中段年级，可谓是“无图不成书”“无图不成题”。一般认为，该阶段的儿童认知发展还处于前运算和具体运算阶段，抽象思维水平较低[1]，很难一下子走进符号化的抽象数学世界。从教材编写者和教师的角度来说，设计这些与儿童生活密切相关的、形象生动的数学插图或图示，其中的一个重要功能就是为学习者创建一个情境性的生活数学，以帮助他们更好地理解和掌握抽象数学符号进行问题解决。比如，从小学生身边熟悉的、有趣的事物中选取图示学习素材，可以激发学习数学的兴趣，感受身边的数学[2]，避免学习者在陌生的情境中去学习数学知识;或者，将图示作为一个先行组织者，提供给学习者与新知识相关联的一些功能性、预备性知识，激活他们头脑中已有的背景知识，以帮助他们更好地理解和接受新知识[3]。从情境认知的观点来看，这些图示起到了“在建立意义与学习者经验的耦合以及促进知识技能和体验的连接关系上”的重要的“情境支架”作用[4]。以支撑学生跨越从生活数学到抽象符号数学之间的发展鸿沟。

教学领域中的“支架”（Scaffold，即脚手架），借用普利斯里等人（Pressly，Hogan，Wharton-McDonald，Mistretta，Ettenberger，1996）的描述就是，根据学生的需要为他们提供帮助，并在他们能力增长时撤去帮助[5]。但是，小学生在面对这些数学图示时，情况并非总是如此。一些数学图示呈现的信息对于他们来说，有时难以达到系统性和完整性的知识建构要求[6]，有时在他们容易理解的算式上呈现无关的或者多余的信息，不仅没有扮演“脚手架”的角色，反而成了干扰他们正确理解数学思想和题意的“绊脚石”，对学习者的认知和理解产生了负面影响，形成了图示障碍现象。比如，在小学一年级数学“认识1～5”的单元练习中，有一道图示题中配有西游记中唐僧师徒四人经典形象，用于帮助学生熟悉数字和数量。当要求回答“图中一共有多少人”时，有学生回答：两人，因为另外两个猴子和猪是动物[7]。

看后令人莞尔，却引发我们的思考：本应该给学习者提供帮助的图示如何变成了学习障碍？这些图示障碍有哪些表现形式？如何规避这些图示障碍？这些问题的解决是高质量小学数学教材编写和有效开展图示教学的迫切需要。目前，在小学数学教材图示引发的不良学习影响方面有一定的研究。比如，有研究者对北师大版小学数学教材内的图像表征进行了细致研究，指出如果图像表征运用不当，就会转移学生的视线，偏离学习目标，增加学习难度，与要达到的学习效果背道而驰[8]。有研究者表明，不少数学插图确实存在“负效应”，体现为插图内含信息过多、图文间不相匹配、相似插图引发思维定式等等[9]。从分析来看，现有图示障碍研究更多聚焦于学习材料中图示的图文组合方面，忽略对阅读对象本身的关注[10]，提供的实证性数据也较少。而从学习者的认知角度出发，揭示图示障碍产生的认知机制，这是提升图示设计质量，真正发挥“脚手架”功能的关键所在。

本研究试图通过实证调查与自制测试工具，分析小学数学图示障碍的类型特征，探究学习者面对可能存在的图示障碍时的认知过程以及障碍引发的原因。在此基础上，提出有效降解图示障碍的设计原则，为小学数学教材编写者和教学使用者提供优化图示的设计依据。

二、探寻图示障碍的存在及类型

根据克拉克和梅耶等人的图示概念[11]，本研究中的数学图示是指小学数学教与学过程中所用到的辅助图画、照片、概念图、数据图、流程图以及图文组合而成的图文题等在内的所有静态视觉表征（Visual Representations）。而数学中的图示障碍则是指对学生的数学理解起到阻碍和干扰作用的那部分设计不良的图示。

（一）小学数学图示障碍的一般存在

小学生在数学学习中所遇的图示障碍到底是一种怎样的存在？为了解这一基本情况，我们选取三线城市的一所普通小学中高段4～6年级学生作为调查对象（考虑到低年级学生对问卷题目的理解存在一定的困难，没有选取1～3年级的小学生）。问卷题按李克特五分量表设计，包括学习者对目前数学图示的总体感知、不同教学材料中图示障碍的发生情况以及面对图示障碍的应对方式。回收有效问卷总计295份。

数据显示，虽然学生对“数学教材中图像与对应的文字内容结合密切”的总体看法均值为3.89，但在“数学学习中的一些图像对学习没有帮助”“数学学习中有一些图像让你产生了理解困难或不同的理解”的感知程度上的得分分别为2.84和2.72，接近中位数（M=3.0）。这一数据说明，一方面，数学图示在图文配合设计上总体情况良好，对他们的学习起了帮助作用;另一方面，确实存在一些图示，不仅没有起到学习的支持作用，反而产生了理解困难，甚至成为干扰与障碍。而这一情况在课本和其他学习材料中均有少量体现，均值分别为2.05和2.11。总体上，课本中的数学图示编排质量要略好于其他学习材料。

在遇到这种图示理解障碍时，多数学生会选择直接询问教师（84.9%）、和同学交流（54.9%）或向家长寻求帮助（50.6%）。也有少数学生（39.5%）选择自己理解或不作处理（1.3%），而这部分学生恰恰是图示障碍最经常的影响者。

（二）小学数学图示障碍的典型存在

那么，小学数学教材中存在的图示障碍有哪些典型的樣态？在这些典型的图示样例上，对学习者产生的障碍程度是怎样的呢？

1. 三角互证样例筛选

首先，从人教版、苏教版一至六年级小学数学教材以及配套的教学辅助资料中，由本文研究者和一位小学数学一线教师分头进行，各自挑选出20幅认为可能存在图示障碍的样例。通过对各组挑选的样例进行汇总分析，根据图像、文字以及两者间的组合关系，初步整理出6种类型的10个样例。再组织小学生进行预测与访谈，最后确定有较高可能性产生理解障碍的6个图示作为后续分析样例。这6种图示类型（见表1）包括：（1）图文不符型，文字题的描述和图画呈现的信息不一致。比如，文字描述为每层7间教室，图画显示的是每层6间教室;（2）设问不明型，比如，数数顺序是从上往下，还是从下往上？（3）信息冗余型，图画内容太多，题目的主信息反而被掩饰，或者不需要的题目出现图示，反而成为干扰（无关图示）;（4）动态模糊型，比如，解题所需的信息在变化的图画中没有清晰展示;（5）答案直白型，答案直接在图中呈现，图反而成为学习阻碍;（6）解题定向型，本来有多种算式，图画呈现的却是固定的指向信息。

2. 对比测试工具开发

为减少知识本身的难度对测试的影响，所选典型样例集中于低中学段的1～4年级。接下来，我们将以上所选的6个样例编写成两套测试题（每一题例内含后续分析所需的匹配度、理解度和支持度三维度题项），一套是图示原题，另一套是根据三人研究组对图示障碍点的预判断进行消除改编后，形成新的图示题目。两组对比测试对象同样选择上述同一所小学同一位教师所教的四年级两个班，总计115人。两个班级的前测学习成绩不存在显著性差异，所有测试对象也不存在生理上的缺陷。第一组回收有效试题68份，α=0.894。第二组回收有效试题42份，α=0.974。两组试测信效度良好。

3. 测试结果分析

对于四年级学生来说，尽管测试的样例题目都是先前已经学习过的知识，但是，从第1～4种样例的测试结果来看，原障碍图示测试组的图文不符、设问不明（本研究采用常规理解的“从上至下”的顺序作为正确作答）、信息冗余、动态模糊型图示的错误率分别为23.5%、48.5%、17.6%和88.2%，平均高达44.5%，四种样例图示造成的理解障碍较为明显。而修改后的第二组测试的这前四种图示的错误率分别降到14.3%、9.5%、7.1%和9.5%，平均降比为66.3%。尤其是设问不明型和动态模糊型两组降幅达到80.4%和89.2%，对比非常明显，反映的图示障碍程度最大。

后面两种图示比较特殊。答案直白型图示在消除图画中的明显答案后，用替代图例进行对比测试，虽然修改后的第二组图示例题难度加大，但15.8%的错误率大大低于前四组平均值，也与原答案直白型图示的错误率10.3%相差不大。答案定向型图示的原图只显示三块花片朝下和七块朝上的一种情况，限制性指向明显，学生选择除数字3、7和10之外的组合算式的比例为69.1%，而修改为全部花片朝上的第二组图示测试结果，学生列出两组及以上组合算式的比例为95.2%，大大提升了学生理解的宽度。

三、透析图示障碍产生的内在机制

（一）图示障碍的内在维度分析

为了进一步分析这些典型数学图示障碍的内在特性，在以上的两组图例测试题中，每一组都从学习者角度加入了他们对测试图例的图文匹配度、理解度和对学习的支持度三个维度的感知测试题项（五分量表），分别检测图示内部文字和图片的匹配程度、与学习者认知/理解水平的符合程度以及对学习者学习的支架作用程度（见表2）。

对六类图示两组前后内部维度的得分对比发现，经过障碍消除设计的绝大多数第二组图示，不仅在错误率的结果上比原图示效果更好，在理解度、支持度和匹配度的内部维度都要优于原图示。通过对三种维度得分进行pearson相关性检验发现，第一组原图示中的五种图例以及第二组修改后的六种新图示三维度得分之间呈现出显著相关性，而两组所有的图示在三维度上均两两呈现出正向相关。这说明，图示内部高水平的匹配程度和图示契合学习者的理解程度与图示对学习者学习的支架作用具有正向影响关系。

（二）学习者体验视角的图示障碍认知分析

学习体验是指学习者与他能够作出反应的外部条件之间的相互作用，学习是通过学习的主动行为而发生的，取决于学习者做了什么[12]。而图示承载的内容和呈现方式也更直接与理解活动的心理过程相关[11]。为了进一步了解学习者在面对这些图示障碍时的认知过程，以深度剖析图示障碍的发生机制，我们在完成了第一组原图示障碍测试的学习者中，再随机抽取10位学生进行访谈。学习者被要求细致地描述自己面对各类障碍图示时的理解过程和感知体验。整个访谈过程被录音并转成文字材料。通过整理访谈数据，并结合上述测试问卷数据，发现造成六种图示容易产生理解障碍的因素大体可以归结为三类：图示内部缺乏一致性（图文不符、设问不明）、图示内容编排不合理（图示冗余、动态模糊）和图示信息呈现不恰当（答案直白、解题定向）。

1. 图示内部缺乏一致性

在面对第一种图文不符型图示（课桌椅计算）时，大多数学生列式作答会同时参考图和文字（66.2%），而不是单一地凭借图像（13.2%）或者文字（20.6%）。他们中的大多数人（70%）也意识到了图像和文字内容存在不一致，对图像内容的正确性产生了质疑（“有可能图是错的”“这个图有可能和题目不一样”）。本来学习者是想借助图示（脚手架）来解题的，现在他们对图示产生了质疑，反而变成解题时多出来的一道理解障碍（绊脚石）。当问及如何应对时，受访学生反映他们多会采取忽略图像的做法（“那就只看文字就好啦”）。因为，已有的图示经验告诉他们：通过文字进行作答有更高的正确性。也就是说，在这一情形下，图示设计的“脚手架”本意完全失去了。

对于测试题中的设问不明型障碍图例（数猴计数），大部分小学老师认为一般按照“从上往下”的常规理解顺序，选择“第2”作答。其实，课本并没有给出这一“标准答案”。在10个访谈学生中，选择“第2只猴”作答的有6位，选择“第4”作答的有4位。学生都已经懂得用“第几”来表示顺序，也认为“从上往下”或“从下往上”的顺序都可以选择，但因为只有一个答案，也没有指定顺序，在答题时，他们大多表示“当时有点犹豫”。图示内部信息指示不明，“脚手架”最后成了一种解题的“困惑”和“干扰”。

2. 图像内容编排不合理

在面对信息冗余图例（乘车问题）时，大部分访谈学生都表示，“文字题目已经告诉我学生数量了”，所以“旁边的一群学生没什么作用”“后面的博物馆对我做题没有什么帮助”，而大巴车上的“限乘49人”这个“关键信息放大一些会更好”“这个信息在图里显得太小了”。他们认为，如果将与文字内容完全相同的图像进行删减，就可以使得关键信息醒目地呈现。情境支架中的信息过多，导致关键信息不明显，图示障碍就产生了。

在面对动态模糊型图示（纸鹤计算）时，学生的作答结果多样。他们在解题过程中已经意识到，需要通过结合图示中千纸鹤前后的变化来进行列式，但图中千纸鹤的数目总体没有发生改变，只是位置不同，所以产生了多种不同的列式结果。“他们本来是每人有一只的，后面每人又折了一只，所以用加法（3+3=6）” “最开始那幅图的桌上是没有千纸鹤的，后面第二幅图桌上有了千纸鹤（0+3=3）”“他们开始的时候手上一共有三个，后面放到桌子上，手上就没有了（3-3=0）。”图示前后变化过程十分模糊，导致学习者难以建构出千纸鹤的数量变化过程，对使用哪种算法和数字组合产生了不确定性，图示障碍随之产生。

3. 图示信息呈现不恰当

访谈中，当问及学生，面对答案直白型图示（黑兔计算）时“你是直接看图数数还是计算得出结果的”，虽然多数学生认为，“还是要计算，因为老师会扣分”“因为画有可能会不标准”“如果老依靠图，以后没有（图）就不会做了”。仍有2位学生反馈，对于“列式计算和照图数数”的两种作答方式，“觉得还是数比较好”，“万一是大一点数的话，计算有可能会出错”。但是，与面对面的访谈不同，在上述进行的无记名测试问卷中，却有将近一半比例（45.6%）的学生是直接“通过数图像中黑兔的数目得出”答案“5”（选择题），只有54.4%是“通过分数的乘法计算得出”，两种方式作答的人数差不多各占一半。说明学生的作答在没有教师列式计算的要求下，受到直白图示答案的影响非常明显。

在面对解题定向型图示障碍（花片计算）时，测试问卷结果显示，61.8%的学生是根据“图示中已经抛出的花片结果”来列算式（数字3、7、10之间的加减列式），只有38.2%的学生依据“现实中随机抛花片的结果”来列算式（除数字3、7之外的其他10以内的加减数字组合）。在面对面的10个访谈对象中，8位学生都表示“直接看图片中的两种花片结果”，只有1位学生认为“和抛硬币一样会抛出不同的花片”，所以他所列的算式符合随机组合。另有一位学生，“看到图中右边一半”，所以列出了“3+2=5”的错误算式。显然，这些图示呈现的信息没有很好地对应开放性的文字题意——“把10个花片抛一抛，写出算式”，反而固化学生解题思维，阻碍了学习。

（三）基于多媒体学习理论的图示障碍认知分析

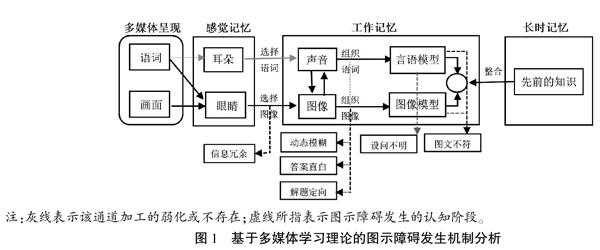
数学图示具有图画和文字两种媒体要素，小学生所进行的看图解题是一种典型的多媒体学习。因此，通过多媒体学习认知理论的双通道、容量有限和主动加工的三个基本假设[13]，可以分析不同的数学图示在被学习者“选择—组织—整合”的认知过程中产生障碍的认知机制。由于小学数学图示一般以纸质或屏幕的图文形式呈现，语词和画面两种要素都是先通过眼睛感知（不存在耳朵通道选择词语的感觉记忆过程），再进入工作记忆中组织形成言语模型和图像模型，最后通过与先前知识的整合，完成整个认知过程。不同的图示障碍发生在不同的认知阶段。

1. 感觉记忆向工作记忆转化阶段

信息冗余型图示障碍发生在所有6种图示的认知最前段，即在眼睛看到图像之后，感觉记忆转换为工作记忆的选择过程中。由于人的认知容量有限，无关或冗余信息导致无关认知容量加大，基础认知容量减少[14]，使得学习者将珍贵的认知资源作用在了无意义的图示内容当中，影响了学习效果。

2. 工作记忆中组织语词和图像阶段

动态模糊、答案直白和解题定向三种图示障碍常发生在工作记忆的组织语词和图像的认知阶段。学习者在工作记忆中对图像进行加工时，会受到不合理图像内容的明显影响，造成错误的推理或省略了必备的认知过程，弱化了向组织词语的转换（文字题意本身的理解），强化了图像模型的组织。

3. 工作记忆中言语和图像模型建构阶段

设问不明型图示障碍发生在工作记忆组织语词向言语模型建构的认知过程中。由于缺乏明确的文字描述，学习者难以将语词组织成完备的言语模型，从而弱化或忽略言语模型的组织，进而影响言语模型和图像模型的整合理解，产生解题障碍。

4. 工作记忆中言语模型和图像模型整合阶段

学习者在面对图文不符型图示时，同时开启语词和图像加工通道，在工作记忆的认知过程中，当学习者发现言语模型和图像模型所建构的意义不匹配时，无法将两者整合成一致理解，认知障碍随之产生。在实际的访谈中也发现，当两者发生矛盾时，更多的学习者倾向于将言语模型作为主导认知通道，从而造成学习者在前期图像模型组织上的认知浪费。

四、研究结论及启示

綜上，不管是从教师和研究者作为成人学习者的感知分析，还是从小学生作为在场学习者的感知和典型图例的实证测试，都印证了图示障碍在小学数学教学过程中的普遍存在，且在学生中不体现性别差异。从数学图示的设计上来看，图示内部缺乏一致性、图像内容编排不合理以及图示信息呈现不恰当是形成图文不符、设问不明、信息冗余、动态模糊、答案直白和解题定向6种典型图示障碍的三大主因。这些设计不当的典型数学图示不仅容易造成学习者较明显的理解障碍，产生解题错误，而且在某种程度上限制了学生的开放思考以及对数学符号和试题本身的深度理解。

以上研究表明，经过改善设计的图示障碍能够得到有效的控制和消除。研究揭示的图示障碍产生机制为图示的优化设计提供了有益启示：在编制、设计和使用小学数学图示时，如能遵从以下三个学习设计原则，将有效避免图示障碍的产生，回归图示本身赋有的支持学习的“脚手架”功能。

（一）多媒体学习理论的匹配设计原则

图示障碍发生在多媒体学习理论中词语和画面两个加工通道的不同阶段。因此，在编写图示例题时，要将“图文匹配”原则放到首先考虑的重要位置，确保数学图示题中的图画与文字形成内部理解的一致性。其次，再考虑图文两大要素在“选择—组织—整合”过程中的作用机制，合理编排图像内容，准确呈现题目信息，控制无关信息，减少冗余信息[15]，杜绝“带有答案指向”（过简）和“含糊不清”（过难）的两个极端设计。

（二）学习者中心的设计原则

表面上看，关注图文的内在一致性（匹配度）似乎可以解决数学图示障碍的消除设计问题。测试调查发现，部分图示障碍不能单纯以答题的错误率进行判断，一些隐性障碍的消除必须深入到学习者的认知当中，关注图示是否符合学习者的理解水平（理解度）以及是否能真正对学习者学习起到支持作用（支持度）。教材插图和其他图示的设计如果脱离于学生真实的学习过程，其设计将犹如构建空中楼阁。因此，教材编制者不能以用户中心的设计思维，将图示设计的重心放在作为教学使用者的教师角度，更多关注的是用户使用的“行动理论”，聚焦的是“教师如何工作（教学）”。相反，应从用户中心转向学习者中心设计，聚焦“学生如何学习”，帮助他们跨越专长知识的鸿沟[16]。新型的教学范式要求教师基于学生知识建构的需求设计“脚手架”[17]，以学生学习为基点进行图示例题的教学设计，在图示设计与日常教学之间形成良性互动，在知识、图形、文本和学生的理解互动中寻求最有效的方案[18]。

（三）基于深度学习的情境支架设计原则

深度学习可以理解为一个人能够将某种情境下所学的知识应用于新情境中的过程，本质上是“面向迁移而学”[19]。在这一过程中，教师采用情境模式的深度学习教学至关重要。即，首先将核心知识的教学“情境化（Contextualization）”，激发联系与理解，然后通过“去情境化（Decontextualization）”促进学生知识的抽象化和概念化，最后“再情境化（Recontextualization）”進行相似情境的问题解决[20]，最终发展学生可迁移的深度学习能力[21]。

传统的小学数学课堂，教师普遍缺乏深度学习的情境教学设计意识，在进行抽象的核心数学知识教学时，常常跳过了“情境化”环节，直接采用“去情境”的干巴巴的符号教学，容易形成不可迁移的“浅层知识”。而图示例题的设计，在很大程度上，就是通过图文创造的问题情境，起到情境性学习支架的作用。因此，要回归图示的“脚手架”功能，设计者和教学使用者应特别注意设计和使用的区间和时机：一种情形是，当学生从现有抽象符号水平难以直接达到潜在的发展水平时，应将数学问题置于图示题的情境中（情境化），或激发兴趣、或联系生活、或辅助理解，以支架他们跨越最近发展区。再通过学习者自我概念化过程（去情境），达到抽象符号运算的潜在发展水平;另一种情形是，当学习者面对相似的更复杂的问题情境时，设计图示支架的作用是将问题“再情境化”，以发展学生问题解决的远迁移能力。而当学生面对的是一些比较简单的、现有抽象水平能够解决的数学问题时，则可不用情境图示，直接“去情境”进行符号教学，否则图示有可能成为学习的冗余和障碍。同时，在学习者完成“情境化—去情境—再情境化”的学习任务后，教师有必要拆除“脚手架”进行“再去情境”（脱境），回归到文字符号题例进行数学思维的概念化精炼，形成一般化的数学知识，最终帮助学生从情境化的“生活数学”走进符号化的“抽象数学世界”[22]，实现抽象符号的深度理解（如图2所示）。

随着数字多媒体技术的快速发展与应用普及，一个读图与读屏的时代已经到来。当越来越多的图文组合静态图示（当然还有图文与声音动画组合的动态图示）内容出现在小学生的纸质和数字教材、学材、课件和网络资源中，对于图示材料的设计者和教学使用者来说，如何最大程度消除潜在的图示障碍，更好地发挥图示“脚手架”功能来帮助学生学习，是当下需要面对和解决的共同课题。未来，借助科学的学习工具展开实证研究来探寻视觉表征的更优化表达已成为新的研究方向[23]，也对教师提出了优化和使用图示支架的更高要求[24]。

[参考文献]

[1] 蒲志安.小学低年级教材插图的认知、教育功能与定位分析[J].课程·教材·教法，2008（9）：7-10，40.

[2] 中华人民共和国教育部.义务教育数学课程标准（2011版）[M].北京：北京师范大学出版社，2012：65.

[3] 杜军.“支架式”教学应重视“脚手架”的搭建[J].教育理论与实践，2005（14）：51-53.

[4] 高文.情境认知中情境与内容的作用——试论情境认知的理论基础与学习环境的设计之一[J].外国教育资料，1997（4）：15-18，8.

[5] 闫寒冰.信息化教学的学习支架研究[J].中国电化教育，2003（11）：18-21.

[6] 顾小清，冯园园，胡思畅.超越碎片化学习：语义图示与深度学习[J].中国电化教育，2015（3）：39-48.

[7] 新浪微博.被数学题支配的小朋友[EB/OL].[2021-02-01].https：//weibo.com/tv/show/1034：4447331102425132？from=old_pc_ videoshow.

[8] 聂莉.小学数学教材的图像表征设计研究[D].桂林：广西师范大学，2014.

[9] 刘明.数学插图“负效应”的分析及应对策略[J].教学与管理，2012（11）：46-47.

[10] 宋振韶.教科书插图的认知心理学研究[J].北京师范大学学报（社会科学版），2005（6）：24-28.

[11] CLARK R C， MAYER R E. E-Learning and the science of instruction： proven guidelines for consumers and designers of multimedia learning[M]. Hoboken： Wiley， 2016.

[12] TYLER R. Basic principles of curriculum and instruction[M]. Chicago： University Of Chicago Press， 1949：156.转引自：孙妍.学生为什么不喜欢数学？[D].西安：陕西师范大学，2019.

[13] 理查德·E.梅耶.多媒体学习[M].牛勇，邱香，译.北京：商务印书馆，2006：57.

[14] 理查德·E.梅耶.应用学习科学——心理学大师给教师的建议[M].盛群力，丁旭，钟丽佳，译.北京：中国轻工业出版社，2016.

[15] 王文智.基于认知负荷理论的多媒体教学呈现原则探讨[J].远程教育杂志，2009，17（2）：33-37.

[16] 杨南昌，刘晓艳.学习者中心的技术设计：理念、方法与案例[J].远程教育杂志，2008（6）：14-19.

[17] 钟启泉.最近发展区：课堂转型的理论基础[J].全球教育展望，2018，47（1）：11-20，34.

[18] 金玉宏，肖龙海.促进理解的图示：结构模型和设计原则[J].电化教育研究，2020，41（12）：12-19.

[19] 詹姆斯·A.贝兰卡.深度学习：超越21世纪技能[M].赵健，译.上海：华东师范大学出版社，2020：5.

[20] 吴喆，何善亮.物理教学的“情境化”“去情境化”与“再情境化”[J].物理教师，2017，38（11）：21-25.

[21] National Research Council. Education for life and work： developing transferable knowledge and skills in the 21st century[M]. Washington， DC： The National Academies Press， 2012：5-8.

[22] 李月勝.去情境，从生活数学走向符号世界[J].上海教育科研，2019（12）：69-72，42.

[23] 尚晓青，许佳，陈明璋.数学知识视觉化呈现原理、方法与实践研究——以“分数的初步认识”单元教学为例[J].电化教育研究，2020，41（9）：123-128.

[24] 蔡慧英，董海霞，王琦.教师如何有效设计图示化支架支持STEM课程教学——基于30项实验和准实验研究的元分析[J].电化教育研究，2020，41（10）：73-81.