基于支持向量机的高速公路事故实时风险预测

樊 博，马筱栎，雷小诗，马新露

(重庆交通大学 交通运输学院，重庆 400074)

交通事故是人、车、路、环境为主要因素共同作用下产生的结果，交通事故的发生具有偶然性。然而已有文献研究证明，事故发生前后的交通流参数会出现一定的相同规律的变化，从某种角度而言，事故的发生同时又兼具必然性[1]。由于难以对交通事故的发生作出高度准确的预判，因此研究人员利用事故风险来描述这种不确定性。

国内外对事故实时风险预测的研究中，Xu等[2]使用K-均值聚类将高速公路上的交通流分为不同状态，通过比较不同交通状态下的交通流特征，识别各个交通状态下更能描述事故风险的交通流因素。孙剑等[3]使用上海市快速路检测器数据和事故数据，使用高斯混合模型修正数据后，用贝叶斯网络构建了事故风险模型，实现了对快速路主动风险评估。Yu等[4]使用上海城市快速路数据，使用贝叶斯随机逻辑回归模型建模预测事故风险，同时引入贝叶斯半参数推断方法增加模型的鲁棒性，实验表明半参数下模型具有较高的拟合优度。Li等[5]提出一种长短期记忆卷积神经网络的事故实时风险预测模型，该模型以交通流、信号配时等作为特征，实验表明该模型对预测主线道路的事故实时风险具有可行性。目前国内对交通事故的研究更常见的是基于历史事故记录建立事故集计模型[6-8]，研究多因素条件下事故成因，从而预测未来事故发生的频次，以此量化事故风险[9-11]。这类模型可以用于鉴定事故黑点，有针对性地改善交通设施设备等，但是要做到对道路事故实时监控与预测还需要高精度的交通流参数。为了描述以交通流为主要的事故影响因素与交通事故风险之间的关系，实现实时道路安全监测与事故预判，本文将以高精度的交通流数据为主，结合天气数据，建立模型预测交通事故风险。

1 数据准备

因提取国内高速公路相关数据时受限于道路检测器安装密度较低，数据精度较低，历史事故数据记录不完整等因素，本文将采用加州旧金山I-880N高速公路上相关数据进行分析。在样本构建过程中，本文将以病例对照研究(case-control study)为基础，采用配对式样本构建方式匹配对照样本，以此控制混杂因素(道路线形、坡度、车道数和大小车比例等)对事故风险的影响，从而研究以交通流参数为主的影响因素与事故风险之间的关系。针对I-880N高速公路某全长约25 km的路段，提取其2017年1月～2017年6月期间的交通流数据、交通事故数据和天气数据，下面将对各种数据源特征进行说明描述。

1) 事故数据。

研究时间段内事故记录共计472 起，由于本文研究的是交通流参数与交通事故之间关系，因此仅考虑碰撞、追尾、刮擦等事故形态的记录数据，剔除因车辆故障、货物洒落或记录信息不完整等原因下的事故记录后，用于本文研究的交通事故记录共计233 起。交通事故记录字段中主要包括事故编号、事故发生时间、事故发生位置和事故持续时间等。

2) 交通流数据。

研究路段单向共有33 组检测器，各组分布密度约0.7 km，每组检测器根据车道数不同，包含3～5个传感器。原始交通流数据采集时间间隔为30 s，本文采用的是集成后时间间隔为5 min的交通流数据，数据中包括流量、速度、占有率3种交通参数。为避免因车道检测器故障对采集交通流数据带来的误差，在提取交通流数据过程中，3种交通参数任一参数存在缺失或错误等情况均排除相关记录。

3) 天气数据。

已有研究证明交通运行中的天气因素，尤其是恶劣天气情况下，对交通安全的影响较为明显，不利天气状况下行车确实会增加事故风险[12-13]。因此，本文将天气因素考虑作为特征变量之一，以此提高模型预测的精度。考虑到建模过程中所使用的高精度交通数据，本文将天气分为一般晴天、阴雨天和雾天3种天气情况。

2 样本构建

2.1 样本设计方法

研究交通事故影响因素与交通事故风险之间的关系，实现事故风险实时预测，同时需要事故发生前交通流数据和正常交通流数据。本文将采用流行病学中病例对照配对的方法，以交通事故发生作为病例组，以正常交通流作为对照组，分别以1∶4 的比例[14-15]提取样本。病例组样本包含有效交通事故记录共计233 条，对照组包含932 条样本。按照病例对照的原则，对照组样本选取依据为：1) 与事故记录地点即所选检测器相同；2) 与事故记录日期不同；3) 与事故记录季节、星期相同；4) 与事故记录时间节点相同。

以仅考虑事故前5 min、事故发生位置上游最近检测器的交通流参数为例，若事故发生在P处2017年1月13日，星期五10点42分，则该条事故数据的病例样本为距离事故发生位置A处上游最近一组检测器在2017年1月13日，星期五10点40分的交通流参数。与之配对的对照样本之一应为：P处上游最近一组检测器在2017年1月6日，星期五10点40分的交通流参数。

2.2 备选变量构建

在构建备选变量A时，将变量分为交通流变量A1和 其他变量 A2。 交通流变量 A1包括流量、速度、占有率3参数，其他变量 A2包括天气和由交通流变量衍生的上、下游间差值作为的变量。

交通流变量的构建，时间上将选择事故发生前3 个时间间隔，如图1，事故发生在 t时刻，即提取事故发生前3 个时间间隔点的数据，分别为t1、 t2、 t3。

图1 事故发生时间及时间间隔选取Figure 1 Accident time and selection of time slice

空间上选择事故发生位置上、下游最近2 组检测器，如图2 所示，提取上、下游各2 组检测器数据，分别为上游检测器 up1、 up2和 下游检测器 dn1、dn2。

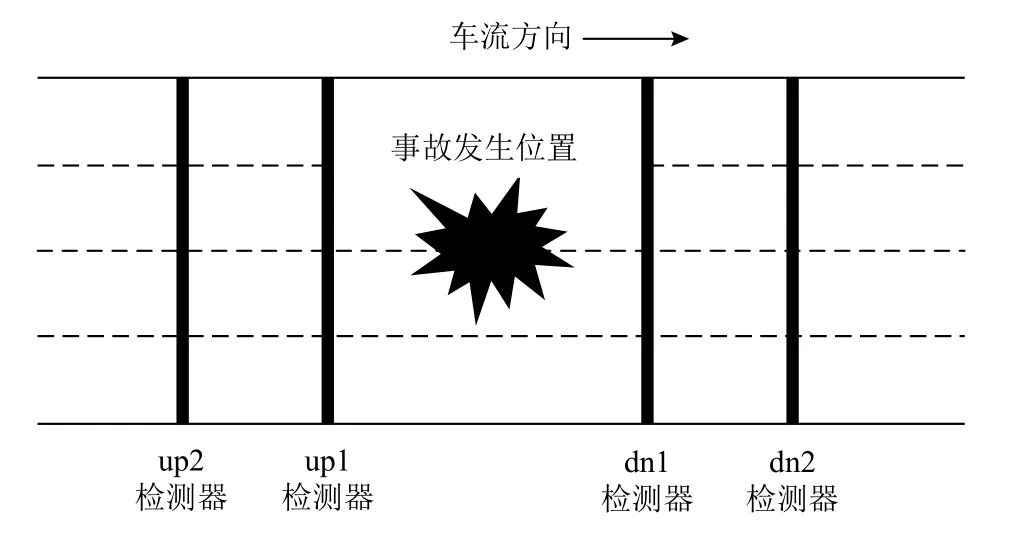
图2 事故发生位置及检测器选取Figure 2 Accident location and selection of detectors station

按照上述时间和空间维度的变量构建，可以提取到事故发生前的交通流变量数据，其数据时空分布如图3 示，其中t为事故发生时刻，各圆点表示交通流参数所在时空位置。

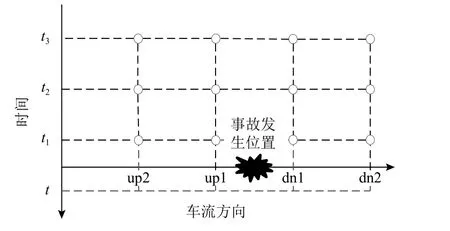
图3 交通流变量时空分布Figure 3 Spatio-temporal distribution of traffic variables

以上交通流变量共同构成变量组A1={fp(tθ),sp(tθ),op(tθ)}，其中各个变量命名规则及其含义见表1。

表1 交通流变量构建1)Table 1 Selective traffic variables for modeling

同时，为充分挖掘交通流特征对事故风险的影响，首先引入事故发生前上、下游交通流变量的差值作为衍生变量，然后加上天气变量后共同组成变

量组 A2={dif_flow(tθ),dif_spd(tθ),dif_occ(tθ),weather}，A2中各个变量命名规则及其含义见表2。

表2 其他变量构建1)Table 2 Selective additional variables for modeling

表2 中d if计算方式为

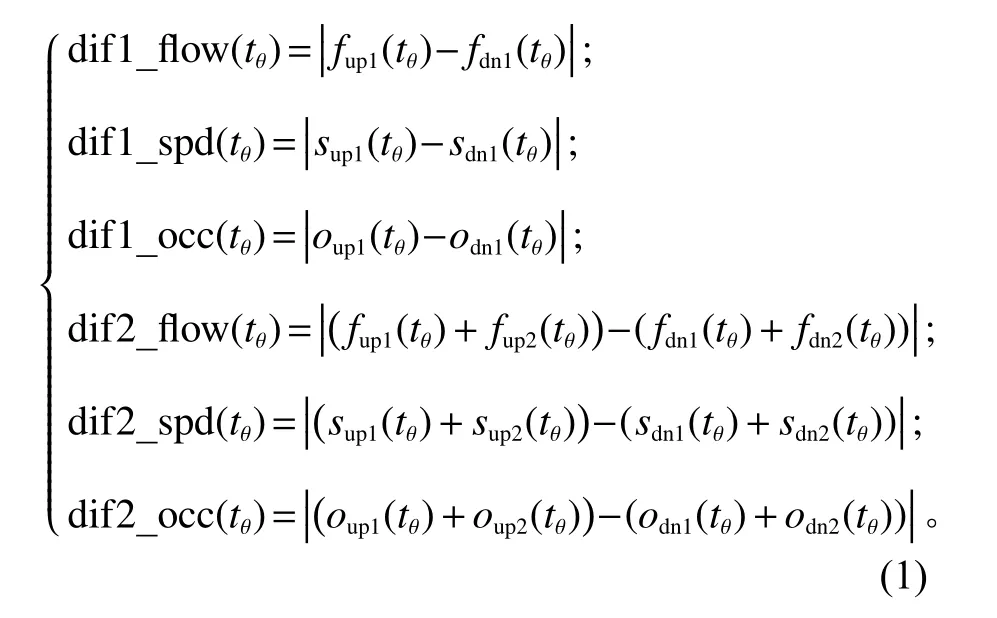
提取交通流变量组 A1和 其他变量组 A2，即可完成备选变量集合 A的构建。

2.3 实验样本建立

通过前2 节对样本的处理和备选特征变量 A的构建即可完成样本建立，样本中交通事故记录组成的病例组成共计233 条，与之配对的对照组共计932条，组成总样本共计1 165 条。同时给每条样本增加标签，病例组样本标签为1，对照组样本标签为0。再按照1∶4的比例将总样本随机分成训练集与验证集，其中训练集包括175 条病例样本和700 条对照样本，验证集包括58 条病例样本和232 条对照样本。

3 基于随机森林的解释变量选择

以随机森林对特征变量进行重要性排序为依据，基于袋外数据误差(out-of-bag error, OOB error)，用平均精确率减少(mean decrease accuracy, MDA)的方法衡量特征重要性，实现变量重要性排序，从而挑选合适的变量组成后续建模的解释变量。随机森林中，MDA计算方法为

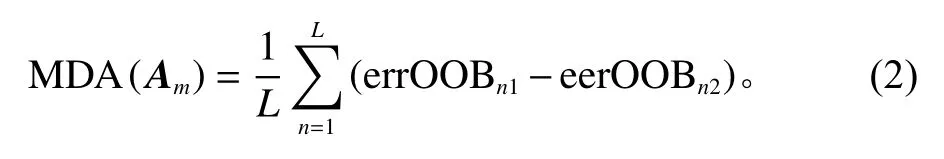
其中， MDA(Am)为 特征变量集合A中特征 Am的平均精确率减少值，m =1,2,3,···；L为随机森林中含有 Am特 征的决策树数量；e rrOOBn1为第n棵决策树OOB 误差率， e rrOOBn2为 第 n 棵OOB中 Am特征引入噪声干扰后重新计算的OOB error，两者计算方式为

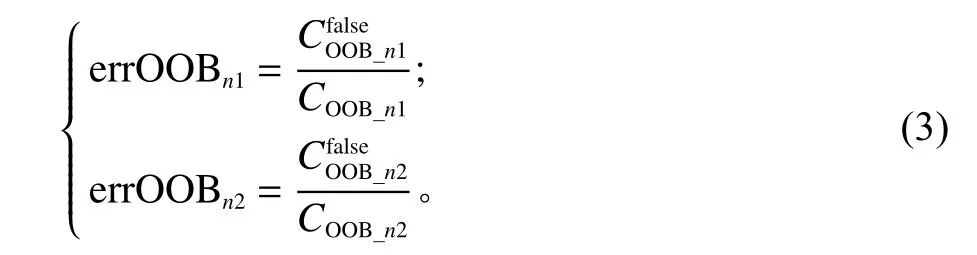
其中， COOB_n1、 COOB_n2为OOB在引入噪声干扰前、后的数量；为OOB在引入噪声干扰前、后在分类器中错误分类的数量。

通过使用Python编程语言实现基于随机森林对特征变量重要性排序，模型中构建300 棵决策树，决策树深度不作限制，OOB误差率在180 棵决策树附近达到最小且稳定的值。实验显示，在事故发生前1个时间间隔，事故发生位置上、下游最近1 组检测器的速度差值(变量d if1_spd(t1))对事故风险影响最大。同时，时间间隔中的t1、 t2对于事故风险预测最为敏感。考虑到实验结果中，M DA值排前10的变量几乎涵盖了时空变化特征和天气影响因素，且随机森林中分类树算法自然有效地避免了多个变量间的交互作用，因此选择这10 个变量作为解释变量进行下一步模型构建。10个变量具体 M DA值如表3所示。

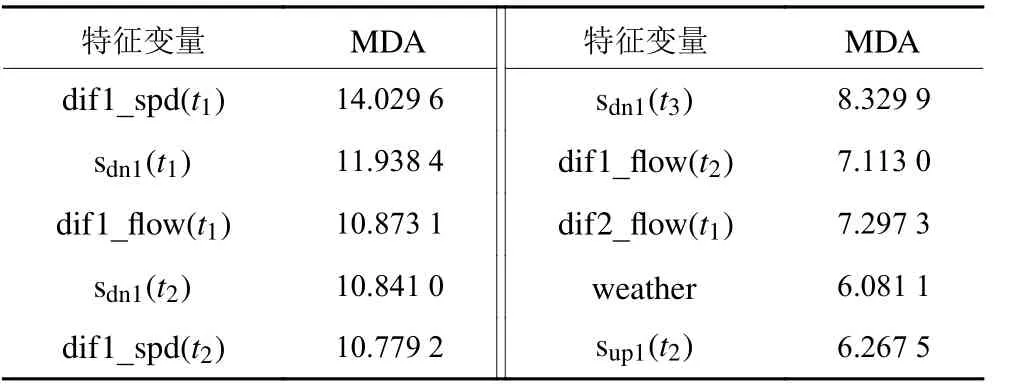
表3 变量重要性排序Table 3 The ranking of variables importance

4 基于支持向量机的事故实时风险预测模型

本文对事故实时风险预测是通过建模来预判高速公路运行状态是否处于“正常运行”状态(病例组)或“事故风险”状态(对照组)，是典型的分类问题。考虑到所使用的数据规模较小，样本维度较高和实时预测对模型的计算能力要求高等因素，选择支持向量机(support vector machine, SVM)，包括线性和非线性SVM，作为本文预测模型，同时考虑到SVM性能优劣主要取决于核函数，故使用常见的核函数对比实验结果以确定最佳核函数。

4.1 支持向量机模型

用SVM作分类问题，首先给定带有标签Y=(y1,y2,···,yN)的 训练样本集 X=(x1,x2,···,xN)，样本集中各个样本一一对应其标签，即可得集合D={(x1,y1),(x2,y2),···,(xN,yN)}， 其中，yi∈{1,−1}。

线性SVM通过学习样本集 D中各个样本特征及其所属分类，通过构建超平面进行分类

式中，w 为超平面 wT+b=0 的法向量，b为其截距。为了方便求解，将式(4)转化为

求解式(5)即可得到 wT+b=0，该超平面可完成对任意样本的分类。

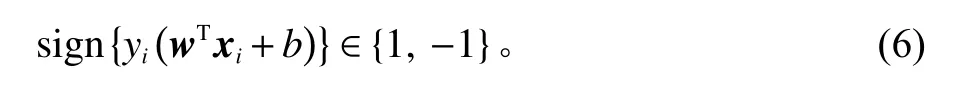
为了解决由于样本线性不可分而带来的误差，还需引入损失函数构造新的优化问题。

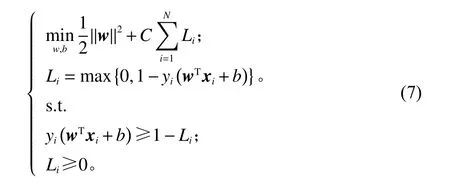
式中， Li为损失函数；C为损失系数。引入松弛变量ξi来处理损失函数，式(7)转化为

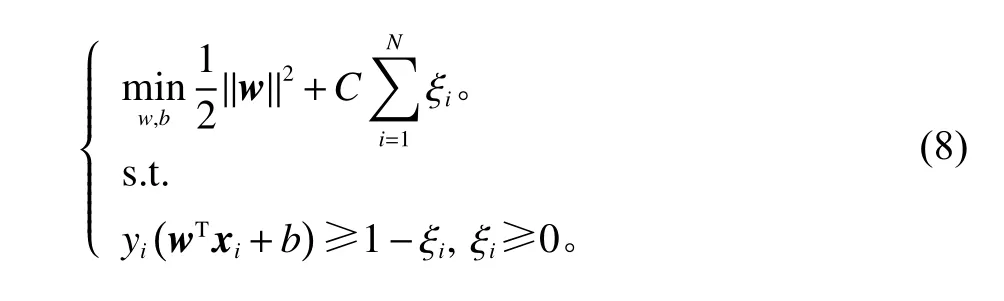
此时，通过引入拉格朗日乘子，可得到式(8)的朗格朗日函数

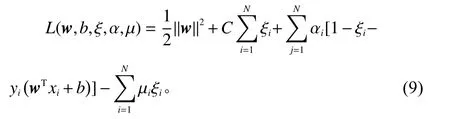
式中， µ={µ1,µ2,···,µN}， α={α1,α2,···,αN}为拉格朗日乘子；令式(9)中w 、 b、 ξ对拉格朗日函数的偏导数为0后，将得到的式子代入原问题(8)的对偶问题。

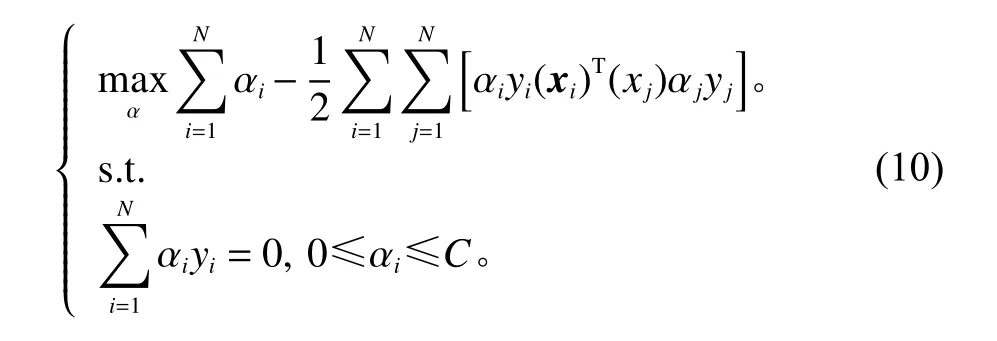
引入KKT条件来求解式(10)包含不等式约束条件的问题，可知对于任意样本总有αi=0或其中，对于满足αi=0的这部分样本不会对超平面产生影响，对于满足1−ξi的样本即为支持向量。

非线性SVM通过引入核函数 ϕ将样本集映射到高维空间后，用超曲面对其进行分类。

此时，优化问题可转化为

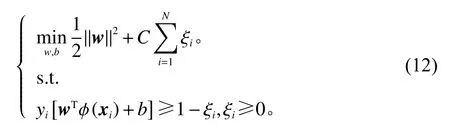
类比式(10)，可对非线性SVM的对偶问题进行求解

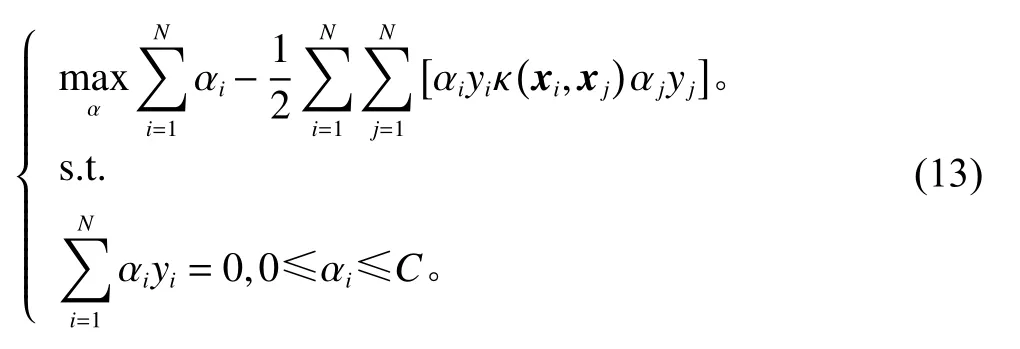
式中， κ(xi,xj)为 核函数ϕ。引入的核函数有线性核、多项式核、高斯核以及Sigmoid核，分别为

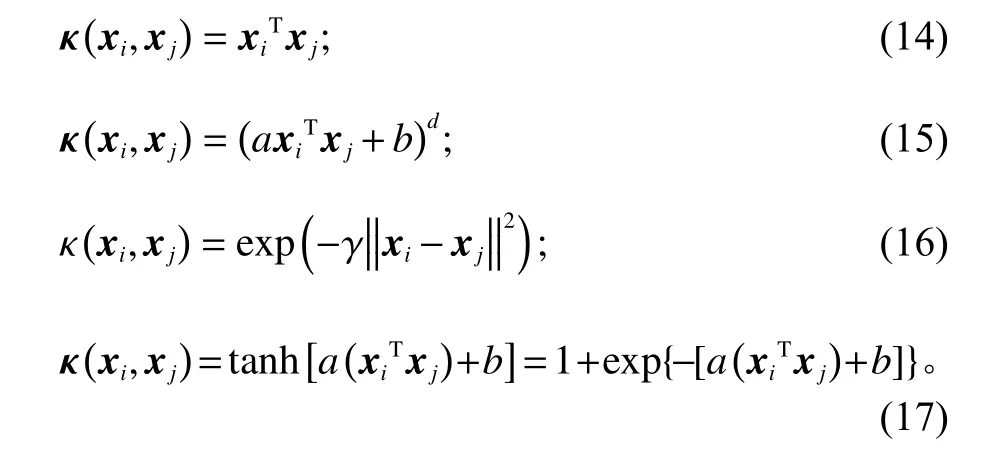
式中，a、 b为 超参数；d为多项式核函数最高项次数，考虑到实时预测对计算能力的要求，本文取d 为3；γ 为超参数且γ ＞0。

4.2 模型评价指标

采用预测病例组、对照组的准确率和AUC值(area under the curve of ROC, AUC) 作为模型预测精度的主要评价指标。首先引入混淆矩阵，见表4。

表4 混淆矩阵Table 4 Confusion matrix

对于准确率，是指分类结果中正确分类占观测值的比例，即病例准确率为T P ， 对照准确率为 T N。对于AUC值，需要计算s ensitivity和 1 −specificity。

式中， sensitivity为真阳性率(true positive rate,TRP)或敏感性。

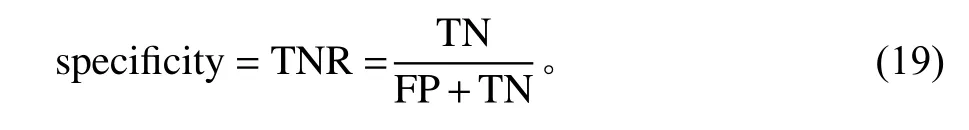
式 中，specificity为 真 阴 性(true negative rate,TNR)率或特异性。

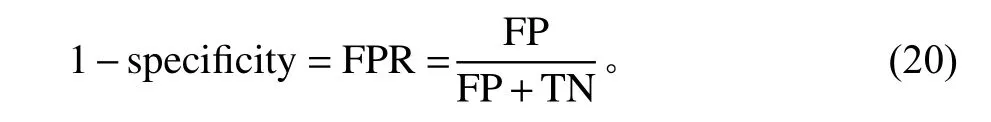
式中， 1−specificity为假阳性率(false positive rate, FPR)或虚警率。

使用 sensitivity、 1 −specificity构造ROC曲线(receiver operating characteristic curve, ROC)后可得AUC值(A UC∈[0,1])来评价模型精确度。

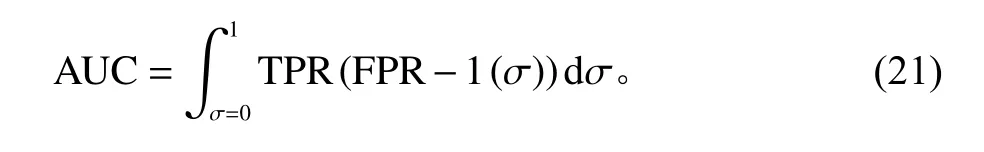
其中，σ为 1 −specificity的 取值，σ ∈[0,1]。

4.3 实验结果分析

通过使用Python编程语言实现基于上述多种核函数的SVM模型，首先按照已有样本集中训练集和测试集进行试验，然后再重新按照1∶4 的比例建立样本集，用各种核函数重复5 次实验后取平均值得到实验最终结果。多项式核函数中d 取3，其他超参数a、b、γ和C 在多次实验后组合保证能使准确率维持在较高水平下调参取值。具体各核函数下的SVM模型的准确率见表5。

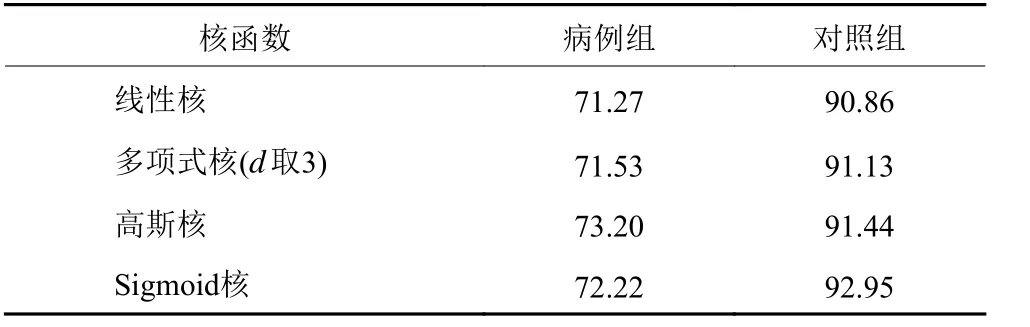
表5 模型分类准确率Table 5 Performance of SVM in different kernel functions %

同时通过式(21)计算得各核函数下的SVM模型结果AUC值，以此6 次更换样本集的实验结果AUC标准差见表6。

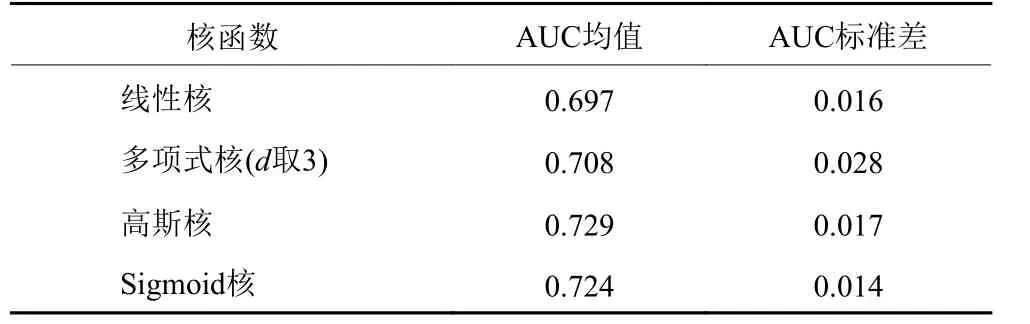
表6 不同核函数下的模型AUC值及其标准差Table 6 AUC value of SVM in different kernel functions %

表5 与表6 显示，使用高斯核、Sigmoid核作为SVM的核函数有较好的预测能力。其中，使用高斯核时识别预判事故风险的准确率达73.20%，对正常交通流的分类达91.44%，AUC值为0.729；使用Sigmoid核时识别预判事故风险的准确率达72.22%，对正常交通流的分类达92.95%，AUC值为0.724。同时，不同核函数下SVM模型对正常交通流(对照组)的分类准确率均高于事故风险交通流(病例组)。根据已有研究和本文实验结果分析，这主要是相比于事故风险下的交通流运行状态而言。交通正常运行状态是常态，这就导致对照组样本数量更加丰富，样本对正常交通流的描述更加详细；而且影响事故风险的因素众多，无法用某特定的特征变量集合对所有事故风险进行描述。

5 结论

本文借助高精度的交通流数据，同时考虑天气因素，以交通流为主要影响因素建模，实现对高速公路事故风险的预判。通过真实数据设计实验验证模型的可行性，完成的主要工作及结论如下。

1) 提出基于随机森林算法筛选影响事故风险的重要特征变量，并针对小样本、高维度的数据集提出了重要特征影响下的SVM模型，然后使用和对比多种核函数下的模型预测准确性。实验结果显示采用高斯核、Sigmoid核作为支持向量机的核函数时，模型预测能力最佳。

2) 实验结果显示，通过把重要特征输入到SVM模型中，即可有效地识别和预判事故风险，相比目前预测事故病例事故模型70%的准确度，本文建立的SVM模型不仅能对病例达到73%左右的预测精度，同时经随机森林算法排除了冗余变量，能有效降低模型计算负荷，为后续交通管理人员对事故的反应、处理和管控争取到相对更多的时间。

针对不足之处，本文进行分析和建模的相关数据来自加州I-880N高速公路，其与我国高速公路有所差异，因此将模型应用到我国高速公路上时，还需根据实际情况(道路车道数、检测器安装密度和数据采集误差等)再次进行分析验证。针对后续研究，将考虑引入交通流预测模块，将预测的交通流参数输入到模型，实现事故风险多步预测，可帮助交通管理人员对事故的反应、处理和管控的同时，还可将事故风险情况借助公众出行交通信息服务系统提醒公众，进一步提高高速公路主动安全性。