轨道交通备用电源模型搭建及参数辨识研究
丁龙海,王家捷,刘国龙,岳晓燕,刘 明,郭伟华
(青岛亚通达铁路设备有限公司,山东 青岛 266111)
1 轨道备用电源应用及模型研究现状
我国高速动车组自2007年发展至今,从“和谐号”到“复兴号”,从时速200 km到时速350 km,高速动车组技术不断的升级,给广大人民群众的出行提供了便利,同时也为乘客提供了更好的服务。车辆的辅助供电系统是高速动车组的重要组成部分,为高速列车上的各设备正常工作提供保障,确保机车能够为此在正常的工作状态下运行,同时为高速列车上的工作人员和乘客提供工作和生活上的各种便利条件[1]。车辆辅助供电系统由辅助电气设备、辅助电源等组成。备用电源是辅助电源的重要组成部分。国内外主流高速动车组所装备的备用电源为镉镍碱性蓄电池,其具有适应温度范围广(一般工作环境温度-40 ℃~45 ℃)、循环寿命长、维护周期长、可靠性高等特点。
在今年的国家“十四五”规划中提到“要构建数字化应用场景,即打造智能制造、智能铁路”,这势必会带来了技术升级。目前,备用电源装车后能采集整组电压、电流及温度等信息并将其与车辆通讯传输,所采集的这些信息仅能够反馈当前备用电源的状态,无法利用这些信息进行在线诊断及预测。备用电源在庞大的车辆系统数据中,宛如一座信息孤岛,且与智能化的要求有一定差距。因此,对备用电源的智能化研究势在必行。搭建备用电源基础模型就是该项工作的基础,该模型必须充分考虑备用电源的特性,而且便于拓展,可以为备用电源的状态评估提供依据。因而,构建一个准确的备用电源模型,对可靠性预计、寿命预计及配套设备的开发具有重要意义[2]。由于目前轨道交通备用电源模型方面研究较少,本文结合锂离子电池的相关研究,对轨道交通备用电源模型的构建原理及方法进行探讨。
2 轨道交通备用电源模型原理
轨道交通备用电源属于化学电源。朱方方等人研究指出,常见的电池模型有电化学模型、人工神经网络模型及等效电路模型[3]。其中电化学模型和人工神经网络模型属于非电路模型,等效电路模型属于电路模型。
2.1 电化学模型
电化学模型是在蓄电池电化学反应的基础上所构建的,其通过研究蓄电池的极板、电解液和隔膜之间的电化学反应机理,利用数学公式来描述蓄电池在充放电过程中的电压与电流的关系。电化学模型是从蓄电池的微观组成特性来描述蓄电池的外部特性,因而理论上具有较高精度。但因蓄电池化学反应的复杂性,参数众多且辨识困难,算法求解过程复杂,使电化学模型不易使用。因此常需要对模型进行简化才能加以利用[4]。
2.2 人工神经网络模型
蓄电池内部复杂的化学反应和不确定的温度、使用工况等因素之间关系复杂,因此,蓄电池的外在表现特性与温度、电流并不是完全的线性关系。而人工神经网络具有非常强的非线性拟合能力,学习规则简单,能够精确再现动力电池的非线性特征。人工神经网络模型以BP神经网络算法为基础,将蓄电池的温度、电压、电流等特征参数为输入层,经过隐含层运算,在输出层输出不同荷电状态下的电压,如图1所示。

图1 神经网络模型示意图Fig.1 Schematic diagram of neural network model.
但神经网络方法的误差受训练数据和训练方法的影响很大[5],训练精度依赖于大量的样本数据,当输入数据超出样本数据时,即只适用于原训练数据范围,这就对神经网络模型的广泛应用造成了限制。
2.3 等效电路模型
等效电路模型是电池模型研究中最常用的一种模型。该模型的原理是利用电阻、电容等元器件的特性与电池充放电特性表现的相近性,如利用电阻产生的压降模拟电池加载时的压降,电容的延迟性模拟电极极化电压,理想电压源模拟电池的开路电压等。等效电路模型对蓄电池的各种工作状态有较好的适用性,进而推导出模型电路的状态方程,便于对模型的推导分析和应用。一般应用较多的典型等效电路模型有Rint模型、Thevenin模型、PNGV模型和RC模型,如图2所示。

图2 等效电路模型。(a)Rint模型;(b)Thevenin模型;(c)PNGV模型;(d)RC模型Fig.2 Equivalent circuit model. (a)Rint model;(b)Thevenin model;(c)PNGV model;(d) RC model.
2.3.1 Rint模型
Rint模型是一种电池理想状态的简单模型,其结构仅有一个理想电压源与一个电阻,通过二者串联构成。如图2(a)所示。该模型中Ut为电池的端电压,根据串联电路特性,欧姆电阻R0等于R0两端的电压与回路中电流I的比值。该模型简单,无法准确模拟电池的瞬态特性。
2.3.2 Thevenin模型
该模型考虑了电池反应过程中的极化现象,认为电池的内阻是由欧姆内阻和极化内阻组成。该模型在Rint模型基础上增加了一个RC并联回路,以模拟电池的极化特性,如图2(b)所示。其有电容Cp和电阻Rp是极化时产生的内阻。并联RC回路和欧姆内阻R0用于模拟电池的瞬态特性。相比于Rint模型的单一线性,Thevenin模型已可以表达蓄电池的非线性特征。
2.3.3 PNGV模型
该模型在Thevenin模型的主回路上接入了一个电容元件C,如图2(c)所示。该电容用于描述随着负载电流其时间累积而引起的开路电压的变化。该模型可以描述电池变电流充放电特性。
2.3.4 RC模型
RC模型属于典型的阻容结构。与Thevenin模型不同,该模型额外增加一个RC回路,从而形成二阶RC网络结构。该模型可以更好地表达电池的非线性特征,如图2(d)所示。该模型进一步将电极的极化特性表现出来,即电化学极化和浓差极化。其中Rd和Cd表示电池的浓差极化内阻和浓差极化电容。该模型对电池端电压的回弹特性可以进行很好的模拟。
不难看出,RC网络是可以拓展,形成更高阶的RC模型。清华大学林成涛等人研究结果表明,高阶复杂模型比低阶次模型具有更加精确的预测精度[6]。
2.4 模型选择及解释
通过上述分析各模型优劣,并考虑实际应用过程中的样本试验时间、算法复杂度等方面问题,可选用二阶RC模型进行轨道交通备用电源模型研究工作的基础模型。
在二阶RC模型中,存在有2个RC网络,根据基尔霍夫定律和电流定律,可以得到该模型的动态电路特性表达式(1):
(1)
式中,Ut:蓄电池输出电压;Uocv:蓄电池开路电压;V0:蓄电池欧姆内阻两端电压;Vp,Vd:蓄电池极化RC回路两端电压;Rp,Rd:蓄电池极化电阻;Cp,Cd:蓄电池极化电容;I:回路中电流。
通过转化,可以得到RC回路电压的一阶导数表达式,即电路的状态方程(2)和(3):
(2)

(3)

因此,可以得到该模型电路的输出方程(4),该方程是作为建模最后的输出结果的表达式。
(4)
3 轨道交通备用电源模型参数辨识
在电池模型中,开路电压Uocv,欧姆内阻,极化内阻Rp、Rd,极化电容Cp、Cd等参数,是电池内部反应所决定的,需要在一定条件下通过试验来获取相关参数并进行辨识拟合。
3.1 模型参数获取试验
皇甫海文等人在研究锂电池等效模型时采用了复合功率脉冲试验(Hybrid Pulse Power Characteristic test,HPPC),该试验可以有效地对模型中的各个参数进行获取[7]。HPPC试验是《Freedom CAR电池手册》中的试验,一个HPPC测试中小循环基本是由10 s脉冲放,40 s搁置,10 s脉冲充试,并在不同剩余容量与额定容量的比值(State of Charge,SOC)状态下进行测试。一次循环脉冲的试验方法如图3所示。

图3 HPPC脉冲试验Fig.3 HPPC pulse test.
该试验原目的是测试电池的脉冲性能并计算电池的直流内阻,但经过对试验方法的分析,可以得出电池在一次脉冲放电后经过一段时间搁置的试验方法正好可以模拟电池的“回弹特性”,即电池在放电后,内部化学反应并不是立刻停止,外在表现为放电结束电池端电压迅速上升然后趋于一个稳定值。电池回弹特性曲线如图4所示。图中实线表示电池端电压变化,虚线表示电池的电流变化值。

图4 电池回弹特性曲线Fig.4 Rebound characteristic curve of the battery.
3.2 蓄电池特性曲线解析
根据图4,可以将放电过程分为AB、BC、CD、DE四个阶段。根据对电池充放电的特性,对电池在各个阶段进行研究分析,获得各个阶段的参数。
AB阶段,该阶段是电池由开路状态至电池加载初始时。在刚刚加载时,由于极化电容上的电压不能突变,极化电容起到了抑制作用,而在电池处于开路状态时,可以认为电池的极化电容电压初始值为0,所以AB阶段电池端电压变化是由电池的欧姆内阻R0引起。其表达式如式(5)所示:
R0=ΔUAB/I
(5)
BC阶段,BC阶段的电池在受电池荷电状态降低及欧姆内阻的影响下,电压进一步降低。但由于开路电压和欧姆内阻短时间内变化非常小,可以忽略,因此该阶段电压下降是由于电池的极化电容的变化所致,根据电路原理,此时可以认为电容为零状态响应。该阶段内任一时刻的电压表达式如式(6)所示:
(6)
式中,τ为时间常数。
CD阶段,在电池放电模仿至卸载的初始阶段,电池电压再次突变,电压急剧上升,根据上文分析,极化电容是不能突变,因此该阶段的电压急剧上升是由于电流的突然撤去,导致欧姆内阻不再有压降,而使电池电压迅速反弹。
DE阶段,同BC段类似,该阶段的电压因电池的极化电容而缓慢上升。放电接受后的RC网络结构为零输入响应,根据电路原理,DE阶段任一时刻的电池端电压表达式如式(7)所示:
(7)
根据式(7),可将回弹阶段电池端电压Ut随时间的变化可拟合为:
Ut=k0-k1·exp(-b1t)-k2·exp(-b2t)
(8)
通过试验数据,可以得到k0、k1、k2、b1、b2值,根据式(8)~(12),求得出模型参数的值如下:
Rd=k1/I
(9)
Rp=k2/I
(10)
Cd=1/b1Rd
(11)
Cp=1/b2Rp
(12)
4 轨道交通备用电源模型参数辨识及模型搭建
4.1 模型参数辨识方法
通过上文阐述,已识别出轨道交通备用电源模型中的参数种类,进而通过HPPC试验获取备用电源在不同SOC状态下的电压回弹特性数据,利用所得到的试验数据,对模型参数进行辨识解析。目前模型参数的辨识方法主要有最小二乘法,卡尔曼滤波法等方法。最小二乘法拟合计算简单,但整体误差较大。卡尔曼滤波被估量的统计特性由激励白噪声的统计特性和状态方程确定[8],即依赖噪声。因此,需要一种合适的方法,不仅保证局部有较优的辨识精度,且全局也得保持较好的精度。启发式算法很好的解决了在参数辨识过程中避免了辨识搜索过程因陷入局部最优解,提高了保证全局优的可靠性。本文以退火算法为例,讨论退火算法在轨道交通备用电源模型参数辨识中应用的方法。
退火算法是启发式算法的一种,其利用物理退火过程的自然机理,以在控制温度下降过程中不断搜索,使算法在迭代过程中不仅接受使目标函数值更优的解,而且还能够以一定概率接受比上一个最优目标函数值差的解。并且温度越低,接受概率越小[9]。模拟退火算法的流程如图5所示:

图5 退火算法流程图Fig.5 Flow chart of annealing algorithm.
根据上文的理论分析,对于式(8),在任意解x=[k0、k1、k2、b1、b2]下,通过备用电源模型的参数,根据状态方程,是可以计算出t时刻唯一的端电压值u(t)。因此根据最小二乘原理,确立目标函数如下:
(13)
式中,u(t):回弹阶段,由模型参数计算确定的t时刻电池电压值;U(t):回弹阶段,由试验得到的对应t时刻的电池电压值。
由此将F(x)作为算法的目标函数,在参数定义域内搜索,得到F(x)的最优解,即F(x)的最小值时的一组解(k0,k1,k2,b1,b2),进而通过式(9)-(12)得到当前电流及SOC下备用电源模型的欧姆内阻(R0)、极化内阻(Rd、Rp)、极化电容(Cd、Cp)的数值。
4.2 轨道交通备用电源模型搭建
将不同倍率电流和SOC下的试验数据作为输入,导入模拟退火算法,通过算法运算可得到对应参数k0,k1,k2,b1,b2。利用式(9)-(10)转换为对应的模型电路参数,并将结果导入查表模块。利用simulink仿真软件搭建轨道交通备用电源二阶RC模型。在模型中,以电流作为模型的输入信号,SOC模块根据输入的电流采用安时积分法进行在线运算。将电流和SOC值作为搜索限定条件,通过查表模块(lookup table)功能在线查询得到对应条件下的欧姆内阻(R0)、极化内阻(Rd、Rp)、极化电容(Cd、Cp)的参数值。二阶RC模型的simulink模型[10]如图6所示:
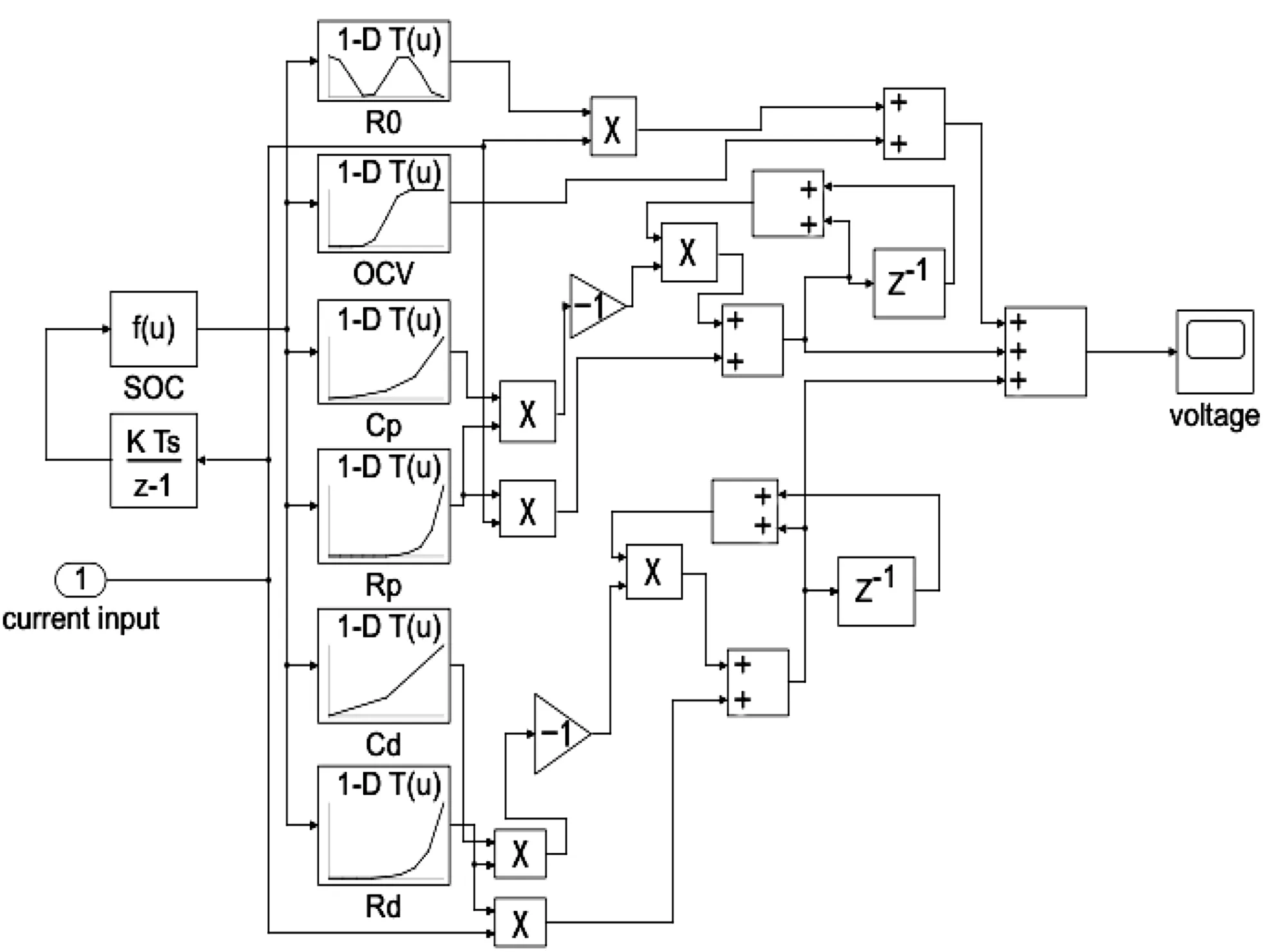
图6 二阶RC模型示意图Fig.6 Schematic diagram of second-order RC model.
5 总结
本文对轨道交通备用电源模型的适用类型、原理及模型参数辨识方法进行了详细的阐述。经过分析讨论,轨道交通备用电源模型可选用二阶RC模型,其电路结构简单,实时性好,能很好的反映备用电源的动静特性。利用HPPC试验对备用电源特性参数进行获取,并将试验数据导入退火算法这一启发式算法,求解式(13)的最优解,进而对模型参数进行辨识,最后利用simulink仿真软件搭建备用电源仿真模型。
轨道交通备用电源模型的研究是对轨道交通备用电源可靠性、寿命预测等研究的基础。高精度的备用电源模型可以很好的反映备用电源正常工作下的特性,并在此基础上进行拓展,如增加环境模块模拟不同环境温度,增加列车工况模块模拟不同使用工况,加入机器学习模块使其根据历史数据进行自学习并模拟寿命的衰减规律等。也可以用于轨道交通备用电源管理系统的开发。综上所述,轨道交通备用电源模型对备用电源的研究及其智能化均具有重要意义。

