转杯粒化装置中高炉渣颗粒换热特性模拟

徐国伟，秦 勤，于庆波

（东北大学 冶金学院，沈阳110819）

我国作为钢铁大国，2018年1—11月钢铁产量为10.13亿t［1］.据估算，钢厂每生产1 t钢铁，会产生0.15～0.3 t高炉渣.钢铁生产过程中产生的高炉渣温度大约在1 500℃，然而这一部分的余热余能并没有得到很好的回收.目前，处理高炉渣主要方法为水淬法，但是该方法能耗较大，成本较高，余热回收率低，环境污染大.针对这些缺点，学者们开始研究干法处理技术.1985年Pickering提出了离心粒化法［2］，又称为转杯粒化法.转杯粒化法的提出是一次十分重要的技术革新.在转杯粒化技术中，熔融态的高炉渣借助离心力和液态熔渣表面张力的作用，被破碎成小液滴，并使熔渣快速冷却为固体渣粒［3］.该过程不需要直接消耗新水，没有水参与剧烈的化学反应，故而也避免了大量具有刺激性、有害的气体产生.同时，在转杯粒化过程中，粒化产生的高温熔渣液滴通过辐射、对流及碰撞导热的传热形式，把热量传递给周围的介质.针对颗粒撞击壁面以后的运动状态，刘兴佳［4］通过实验研究了高炉熔渣粒化装置中颗粒撞壁的恢复系数与颗粒粒径、颗粒速度等之间的关系.为了实现空气与颗粒之间的高效换热并满足后续工艺对炉渣颗粒的要求，需要对离心粒化后的高温炉渣颗粒的飞行和冲击壁面换热特性展开研究.

目前，针对气固两相流动换热方面的研究，主要集中在流化床的流动特性［5－6］，以及传统的燃煤流化床［7－8］.通过前人的研究，已经获得许多气固两相流动及换热规律，但是这些研究针对的都是床层高度较大、颗粒堆积更多的情况.在高炉渣转杯粒化装置中，为了防止颗粒的堆积和黏结，需要减小床层高度，针对浅层流化床中颗粒流动换热研究，Andeen等［9］研究了床层高度为1～4 cm的浅层流化床和水平管束的换热效果.

本文采用三维模型运用CFD-DEM耦合方法，针对高炉熔渣转杯法离心粒化后的熔渣颗粒飞行及冲击壁面的流动换热特性进行数值模拟.通过对颗粒在粒化仓全过程的流动换热模拟，获取颗粒在整个过程的换热情况、粒化仓内部流体区域的温度分布、颗粒的运动轨迹，从而为优化粒化仓的结构及后续的工业应用提供理论指导，提高高炉渣余热回收效率.

1 模型与方法

1.1 物理模型

图1为模拟中运用的几何模型，粒化仓的最大直径为2.24 m，颗粒从粒化仓的转杯中以8 m／s的速度喷射出，撞击壁面以后会沿着壁面流动至颗粒出口，空气作为高温炉渣的冷却介质从粒化仓的上方流出.

图1 粒化仓的二维模型和三维模型Fig.1 Two-dimensional model and three-dimensional model of granulation warehouse

1.2 数学模型

1.2.1 固体相的控制方程

CFD-DEM耦合方法中对于固相颗粒采用拉格朗日框架下的离散单元法［10］进行求解，每个颗粒的运动方程和能量方程如式（1）～（3）所示.

式中：mi为颗粒i的质量，kg；vi为颗粒i的速度，m／s；kc为与颗粒i相接触的颗粒数；fc，ij为颗粒间碰撞所产生的弹性力，N；fd，ij为颗粒间碰撞所产生的黏性阻尼力，N；ki为与颗粒i进行热交换的颗粒数目i；Qi，j为颗粒i与周围颗粒的导热热量，J；Qi，rad为颗粒i与周围颗粒的辐射热量，J；Qi，f为颗粒i与周围流体对流换热热量，J；hc为热传导系数，W／（m·k）；hcov为对流换热系数，W／（m2·k）；σ为玻尔兹曼常数，W／（m2·k4）；εi为颗粒i的发射率；Tlocal为单元网格内颗粒的平均温度，K.

针对空气和颗粒之间的相对运动所产生的阻力，本文采用Gidaspow模型［11］进行求解：

式中：u为速度，m／s；ρ为密度，kg／m3，下标f表示为流体相，下标s为固体相；εs为固体相的体积分数；εf为流体相的体积分数；β，CD分别为曳力系数和阻力系数；dp为颗粒平均粒径，mm；Rep为雷诺数，μf为流体的动力黏度，Pa·s.

1.2.2 流体相的控制方程

模型中的空气为不可压缩流体，一般不考虑高炉渣颗粒跟空气之间的辐射.考虑固体颗粒与流体相互作用的影响，流体相的连续性方程、动量方程和能量方程如式（8）～（10）所示.

式中：kv为计算网格内颗粒的数量，ΔV表示计算网格的体积，m3；μ表示黏度，Pa·s；FD是流体与固体间的曳力，N.

2 参数设置与模型假设

2.1 参数设置

本文采用的模拟参数设置如表1所示.

表1 模型参数设置Table 1 Model parameter settings

2.2 边界条件

Fluent中的进口条件为空气的速度进口，出口条件为压力出口；墙壁材料设置为钢，墙壁条件设为综合换热边界，其中，墙壁和空气的对流换热系数设为20 W／（m2·K），自身的辐射系数为0.6.EDEM中为了防止颗粒堆积，将粒化装置的下界面设置为颗粒移除边界，墙壁与颗粒的碰撞恢复系数设为0.178.

2.3 模型假设

本文考虑到实际情况及模拟计算的可行性，做出如下假设：①忽略了颗粒的内部热阻，把颗粒的温度看作是均匀统一的；②忽略了颗粒的凝固过程，高温熔渣的潜热值为209 kJ／kg，将颗粒的潜热换算成显热附加在整个计算域里；③将模拟计算中的空气看作不可压缩流体.

3 计算结果

3.1 高温熔渣颗粒的换热情况

熔融态的高温炉渣被离心粒化成高速飞行的熔渣颗粒，初始状态时具有很高的速度和温度，在飞行过程中能够进行较强的对流换热及辐射.颗粒撞击到壁面以后会在重力作用下沿壁面流动直到从粒化装置底部离开.

图2为颗粒直径2 mm，颗粒速度8 m／s，空气进口速度1 m／s，颗粒质量流量0.136 kg／s时，粒化装置内流体区域的温度随时间变化云图.由图2可知，在刚开始时，因为颗粒撞击壁面导致自身速度急剧下降，在壁面附近停留时间变长，使得近壁面附近的换热量增加空气温度上升.随着颗粒不断撞击并沿壁面流动离开粒化装置，使得与颗粒接触的空气被加热，高温区不断向上向中推进.

图2 转杯粒化装置内部温度随时间变化云图Fig.2 Cloud diagram of internal temperature variation of rotor granulation device with time

高温熔渣颗粒在粒化装置内的换热分为三个阶段：飞行阶段、撞击壁面并沿壁面流动阶段、颗粒从进风口掉落阶段.由图3可知，粒化装置内温度分布主要分为三个区域，以颗粒飞行轨迹为分界线.在分界线以上为中温区A，分界线以下为低温区B，靠近颗粒撞击壁面附近的高温区C.因为空气进口在粒化装置的底部，所以B区大部分的热量随着空气流动传递到A区，从而使A区温度明显高于B区；高温区C的形成一方面是颗粒撞击壁面使得壁面温度升高对附近的空气进行加热；另一方面是颗粒撞击壁面后速度急剧下降，使得颗粒对近壁面附近的空气加热时间变长.

图3 4 s时刻粒化装置中空气温度分布云图Fig.3 Cloud diagram of air temperature distribution in the granulation device at 4 s time

由图4可知，在颗粒飞行阶段的斜率绝对值最大，因为颗粒初始温度较高，颗粒与壁面之间、颗粒与颗粒之间的辐射换热，颗粒与空气之间的对流换热强度最大；从进风口掉落阶段，颗粒在该阶段与空气之间相对速度较大，对流换热较强；温降速率最小的阶段是颗粒在沿壁面流动阶段，在此过程颗粒与空气的相对速度极小，自身与壁面的接触面积较小，总体的换热强度较低.在颗粒撞击壁面和掉落至进风口时刻都有斜率的变化，这是因为不同阶段的换热条件的改变影响了颗粒的换热效果.

图4 熔渣颗粒在粒化装置中的温度随时间变化曲线图Fig.4 The temperature of molten slag particles in the granulation device changes with time

3.2 空气进口速度的影响

将空气进口速度分别设置为1，2，3，4 m／s，颗粒直径为2 mm，质量流量为0.135 6 kg／s，空气初始温度为300 K，颗粒的初始温度为1 700 K，颗粒的速度为8 m／s，模拟计算得到空气出口温度和渣粒出口温度如图5和图6所示.随着空气进口速度增大，高炉渣颗粒的出口温度以及空气的出口温度都有所下降.比较不同空气进口速度下，高温熔渣颗粒各种换热方式热量的占比，如图7所示.随着空气进口速度增大，对流换热的占比增大；辐射换热的占比下降，主要是因为对流换热增强，导致颗粒温度下降变快，辐射强度随之减小；颗粒沿壁面流动部分导热的热量虽然变化不大，但颗粒换热总量的增加，导热热量的占比下降.

图5 空气进口速度对空气出口温度的影响Fig.5 The influence of air inlet speed on air outlet temperature

图6 空气进口速度对颗粒出口温度的影响Fig.6 The influence of air inlet velocity on particle outlet temperature

图7 空气进口速度对不同换热量的影响Fig.7 The influence of air inlet speed on different heat transfer

3.3 颗粒直径的影响

模拟计算空气进口速度为2 m／s，高温熔渣颗粒速度为8 m／s，空气初始温度为300 K，颗粒初始温度为1 700 K，质量流量为0.135 6 kg／s，颗粒直径分别为1，1.5，2，3 mm，模拟计算得到空气出口温度和颗粒出口温度的变化如图8所示.随着颗粒直径的增大，颗粒出口温度增大，空气出口温度下降.这是因为当质量流量不变时，颗粒直径增大会导致颗粒的比表面积减小和颗粒数目降低，从而影响颗粒的换热效果.同时可以发现，颗粒直径在1～1.5 mm时温降速率最大，表明在此区间颗粒的换热效果较好.比较不同换热方式热量占比柱状图9可知.在颗粒质量流量不变的情况下，随着颗粒粒径的增大，比表面积和颗粒数目的减少使得各种换热方式的热量都降低.其中，受影响最大的是对流换热.

图8 颗粒直径对颗粒和空气出口温度的影响Fig.8 The effect of particle diameter on particle and air outlet temperature

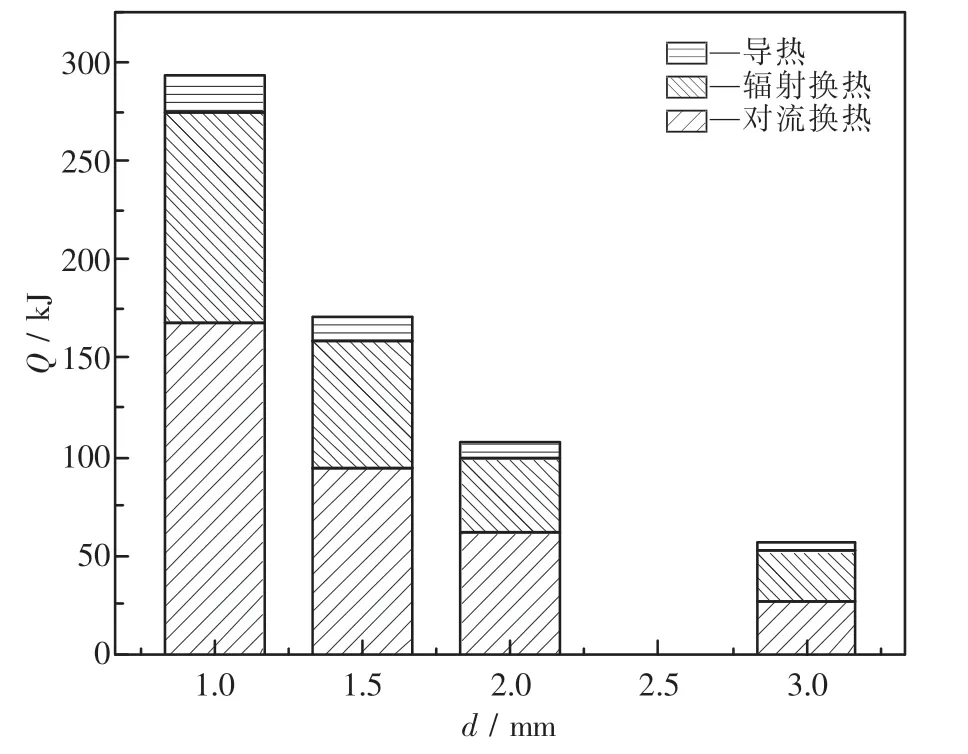
图9 颗粒直径对不同换热量的影响Fig.9 The effect of particle diameter on different heat transfer

3.4 质量流量的影响

模拟计算颗粒直径为2 mm，空气进口速度为2 m／s，高温熔渣颗粒速度为8 m／s，空气初始温度为300 K，颗粒初始温度为1 700 K，质量流量分别为0.1356，0.226 kg／s，空气出口温度如图10，出口渣粒的最小温度如图11.由图10可知，当颗粒的质量流量增大时，空气出口温度也随之增大，主要原因是质量流量的增大增加了计算区域内的颗粒数目，换热量的增大导致空气出口温度增大；从图11可知，虽然质量流量的增加使颗粒数目增大，但是并不影响单个颗粒的换热情况，所以颗粒出口温度的最小值都在一定区间内波动，并没有明显的增大或减小.统计两种质量流量情况下各种换热方式热量占比如图12所示.增大颗粒的质量流量对各种换热方式热量的占比没有影响.

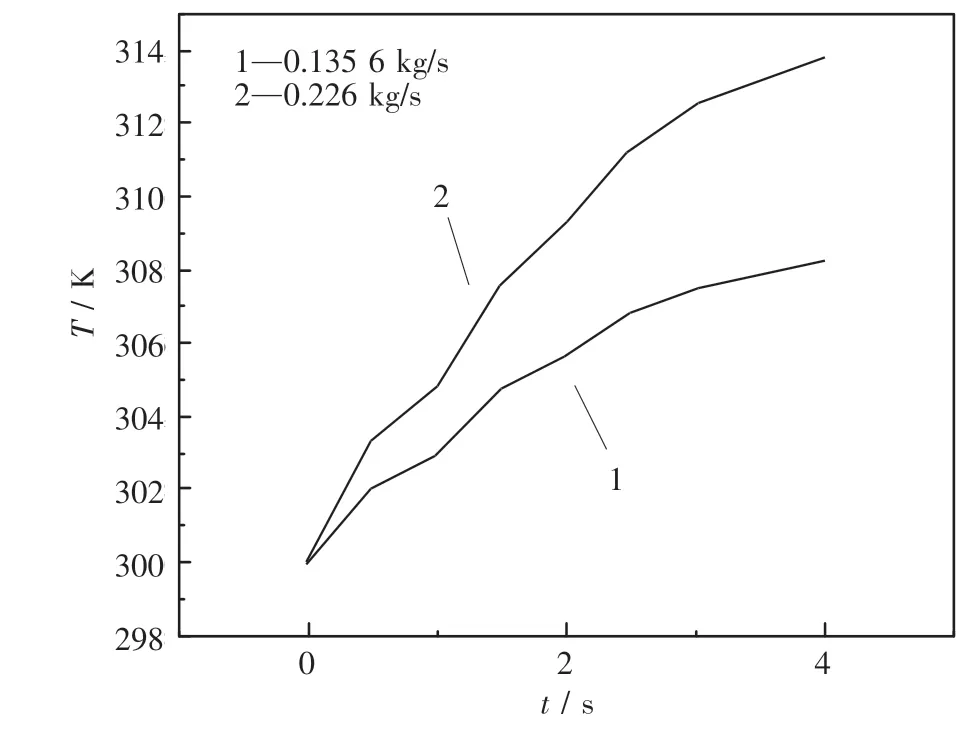
图10 质量流量对空气出口温度的影响Fig.10 The influence of mass flow on air outlet temperature

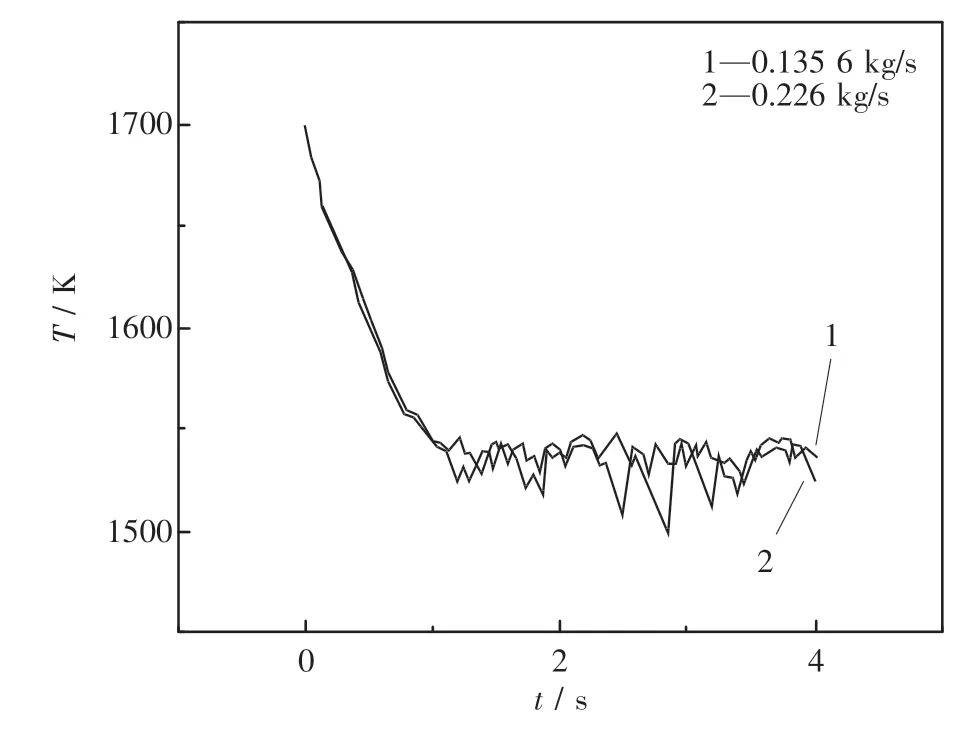
图11 质量流量对颗粒出口温度的影响Fig.11 The influence of mass flow rate on particle outlet temperature

图12 质量流量对不同换热量的影响Fig.12 The influence of mass flow on different heat transfer

4 结 论

（1）粒化装置内部温度最高的部分为颗粒撞击壁面的近壁面区域；颗粒在粒化装置内部运动过程中，撞击壁面时刻的温降速率最快.

（2）高温颗粒在粒化装置内部的换热以对流换热和辐射换热为主，各种换热方式的占比随着工况条件的改变而改变.当其他条件不变，增大空气的进口速度，对流换热的占比随之增大；当其他条件不变，增大颗粒的直径，辐射换热和导热的占比增大；当其他条件不变，增大颗粒的质量流量对各种换热方式的占比的影响几乎没有.

（3）颗粒直径越小，颗粒在整个过程中的换热效果越好.因此，减小颗粒的直径是增强颗粒换热最有效的手段.