剪叉式升降平台起升速度液压控制系统设计与仿真分析*

赵 鑫,纪爱敏,邓 铭,张 磊

(河海大学 机电学院,江苏 常州 213022)

0 引 言

剪叉式升降平台通过剪叉臂的伸缩来垂直升降工作台,并运输工作人员或货物,保持至指定高度,是一种用途十分广泛的专业起升装备[1]。在液压驱动下,增强液压系统的响应速度和工作平台的工作平稳性,对提高升降平台的工作效率和保障操作者的人身安全都至关重要。

为了提高剪叉式升降平台的运动稳定性,国内外学者从不同角度对此进行了研究。MD T I等人[2]用键合图法对剪叉机构进行了研究,并借助仿真软件对其进行了求解,得出了剪叉式升降平台的工作平台的动态特性。付昱[3]建立了双液压缸驱动的剪叉式高空作业平台的数学模型,并借助ADAMS软件,以工作平台的运动稳定性为目标,对模型进行了相应的仿真分析。刘志等人[4]对升降平台的液压系统进行了研究,借助AMESim软件建立了六级剪叉机构的上车液压系统,对在液压管路中配置节流阀、蓄能器以及调速电机的方式进行了比较,分析了相应方案工作平台的速度变化。

在电液控制系统方面,SAMAKWONG T等人[5]设计了具有高速收敛速度的电液伺服系统PID控制器。LIEM D T等人[6]设计了具有前馈网络的模糊电液控制器。

上述研究虽然都从不同方面改善了剪叉式升降平台的运动稳定性,但都存在控制算法较为复杂,使得系统设计难度加大等等的问题。

本文将剪叉式升降平台的液压控制系统作为研究对象,采用模糊PID控制技术对控制器参数进行实时调整,简化算法,解决工作平台起升阶段的运动不稳定现象,提高系统的控制性能。

1 工作平台起升速度函数求解

本研究采用速度瞬心法建立剪叉机构工作平台的速度函数[7],剪叉式升降平台的剪叉臂速度瞬心图如图1所示。

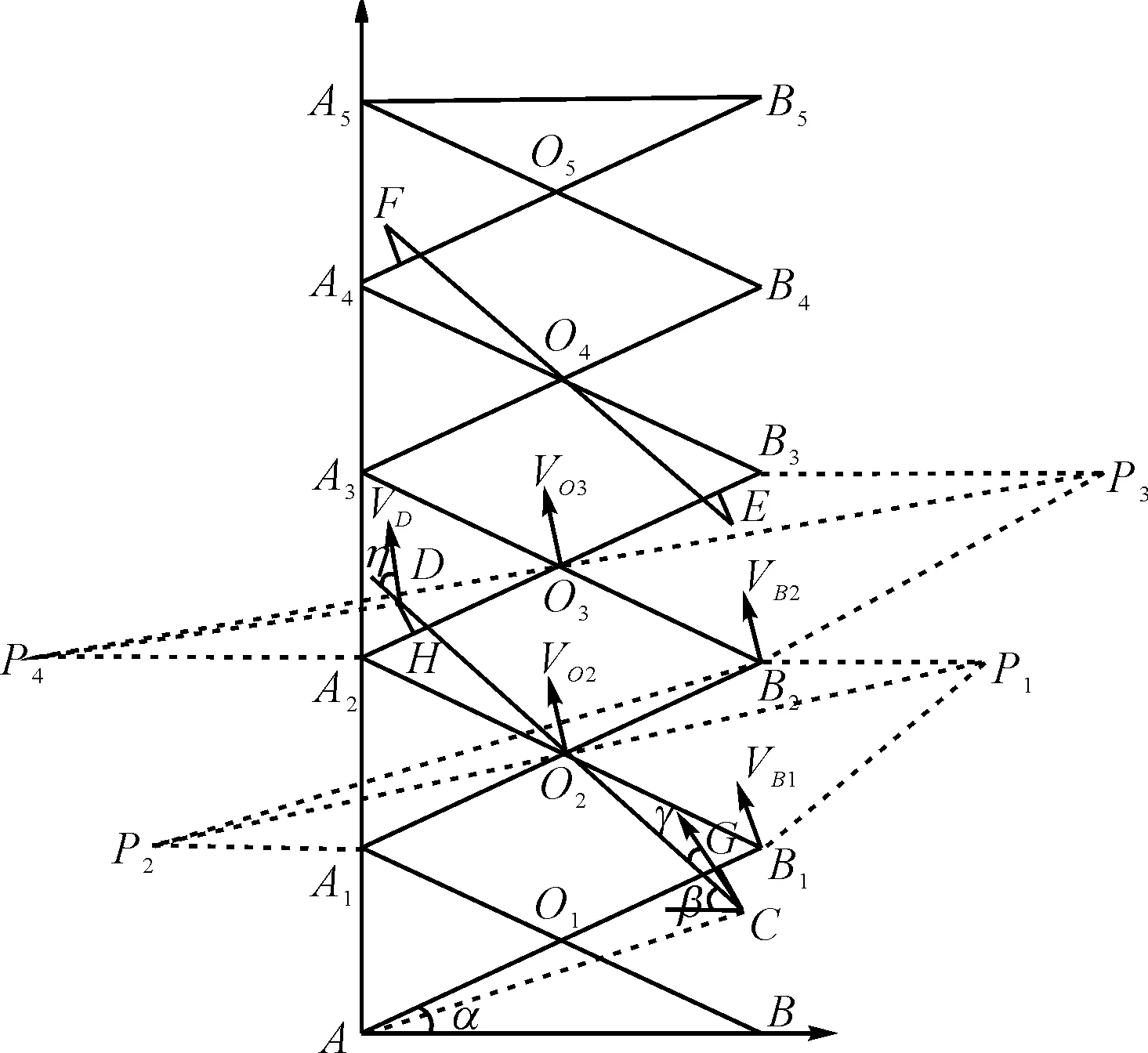
图1 速度瞬心图E、F和C、D—上、下液压缸的安装铰点;以O1～O5为中心的相交线段—五层剪叉臂;A5B5—工作平台;P1～P4—剪叉臂A2B1、A1B2、A3B2、A2B3的瞬心

设剪叉臂的转动角速度为ω,则:

VA5=5ωLcosα

(1)

点D为剪叉臂A2B3上的铰点,点C为剪叉臂AB1的铰点,所以有:

VD=|P4D|ω

(2)

VC=|AC|ω

(3)

由式(1,2)可得:

(4)

由式(1,3)可得:

(5)

设活塞运动速度为V,V为活塞杆和液压缸安装铰点C、D之间的相对速度,V的表达式如下:

V=VDcosη-VCcosγ

(6)

把式(4,5)代入式(6)中,经过变换得到:

(7)

由图1中的几何关系,最终可以得到工作平台速度VA5为:

VA5=

(8)

则:

VA5=V·f(α)

(9)

式中:L—每根剪叉臂长度;a—O1G的长度;b—O3H的长度;L1—CG的长度;L2—DH的长度;α—剪叉臂轴向与水平面之间的夹角;β—液压缸轴向与水平面之间的夹角;η—液压缸轴向与D点速度方向的夹角;γ—液压缸轴向与C点速度方向的夹角;Vi—各个铰点的速度(i对应于各个铰点所对应的字母)。

由式(9)可知:工作平台速度主要取决于活塞运动速度V和角度α。此处以某型号剪叉式高空作业车为例,具体参数为:L=1 800 mm,a+b=1 317 mm,L1+L2=282.8 mm。

笔者将参数代入公式中,得到了工作平台的速度变化情况,如图2所示。

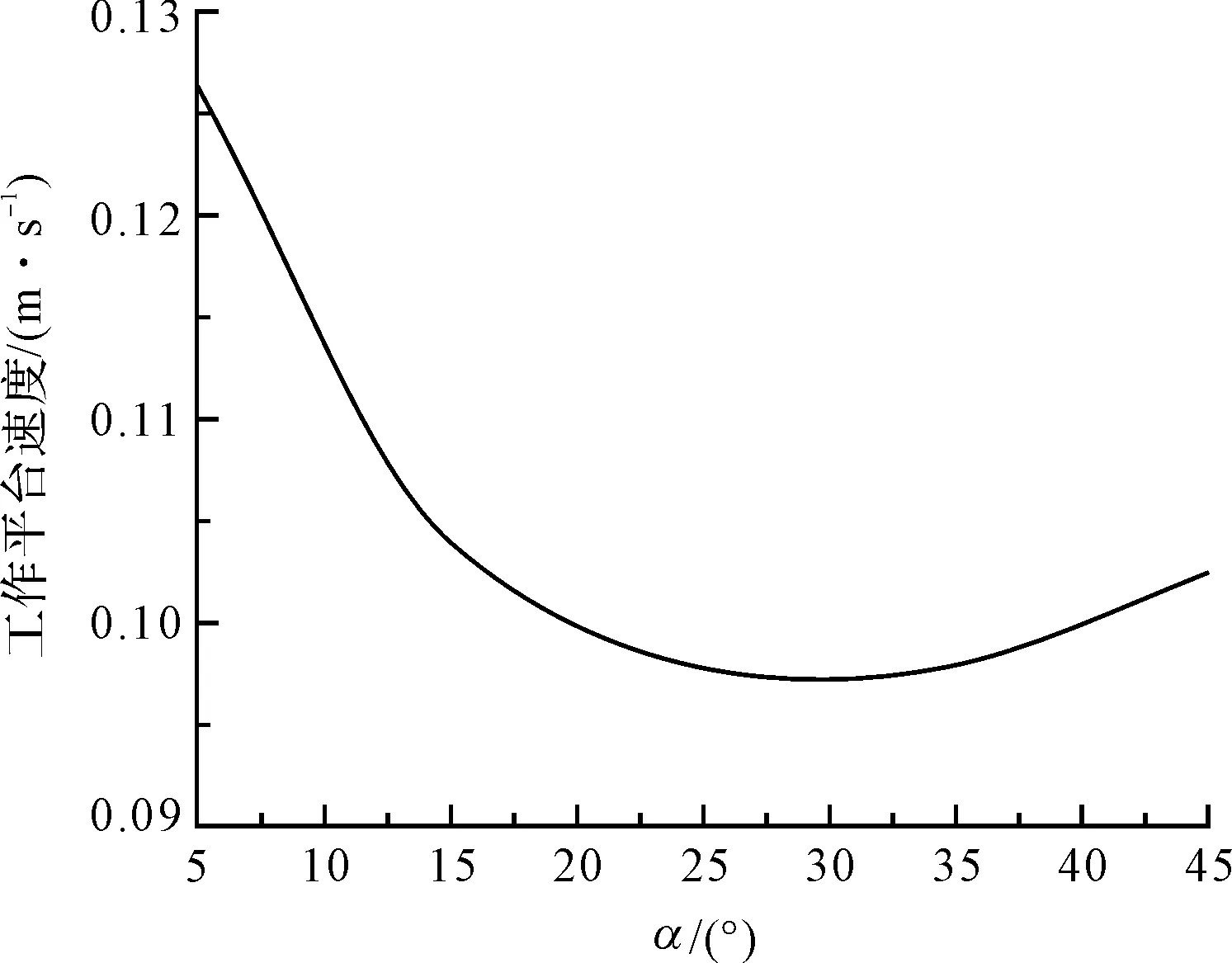
图2 工作平台速度变化

由式(9)和图2可知:当液压缸速度V为某固定值时,随着α的增大,工作平台的速度会先减小再增大,运动并不平稳。而在实际的工作中,期望的工作平台速度为一定值,故需要建立平台的闭环液压控制系统,在该系统控制下使工作平台的速度能快速、平稳地稳定在一个期望值。

2 液压控制系统建模

针对上述的问题,并结合实际的工作情况,笔者建立了该升降平台的液压控制系统的数学模型,并在Simulink中搭建该闭环液压控制系统,通过传统PID控制和模糊PID控制优化系统性能,使得工作平台的速度能快速地稳定在输入的期望值。

2.1 液压系统原理

剪叉式高空作业平台在工作时由液压系统带动液压缸伸缩实现工作平台的起降。考虑到升降平台的运动形式,在保证安全性的前提下,搭建的液压系统原理图如图3所示。

图3 液压系统原理图1—油箱;2—过滤器;3—泵;4—电动机;5—溢流阀;6—电磁比例换向阀;7—开关阀;8—液压缸;9—保护阀

由图3液压系统原理图可知:

首先,压力油从油箱流经过滤器进入齿轮泵,由电动机驱动齿轮泵为液压系统提供动力,压力油进入电磁比例换向阀6,此时电磁比例换向阀右位接通,液压油进入开关阀7-1、7-2,此时开关阀右位接通,压力油进入无杆腔,有杆腔压力油经过保护阀右位流入油箱,形成完整回路(设置开关阀的作用是通过控制线圈得电时间来控制各个液压缸的伸出量),当平台上升至指定高度时,开关阀断开,溢流阀溢流,工作平台不再上升,使工作平台保持在指定位置;完成作业后,电磁换向阀左位接通,保护阀和开关阀右位接通,液压油流回油箱。

2.2 数学模型

综合其各种动态过程,为了简化系统,且不失一般性和典型性,笔者对单条液压缸回路系统进行合理的假设,并进行必要的简化,简化后的闭环液压控制系统如图4所示。

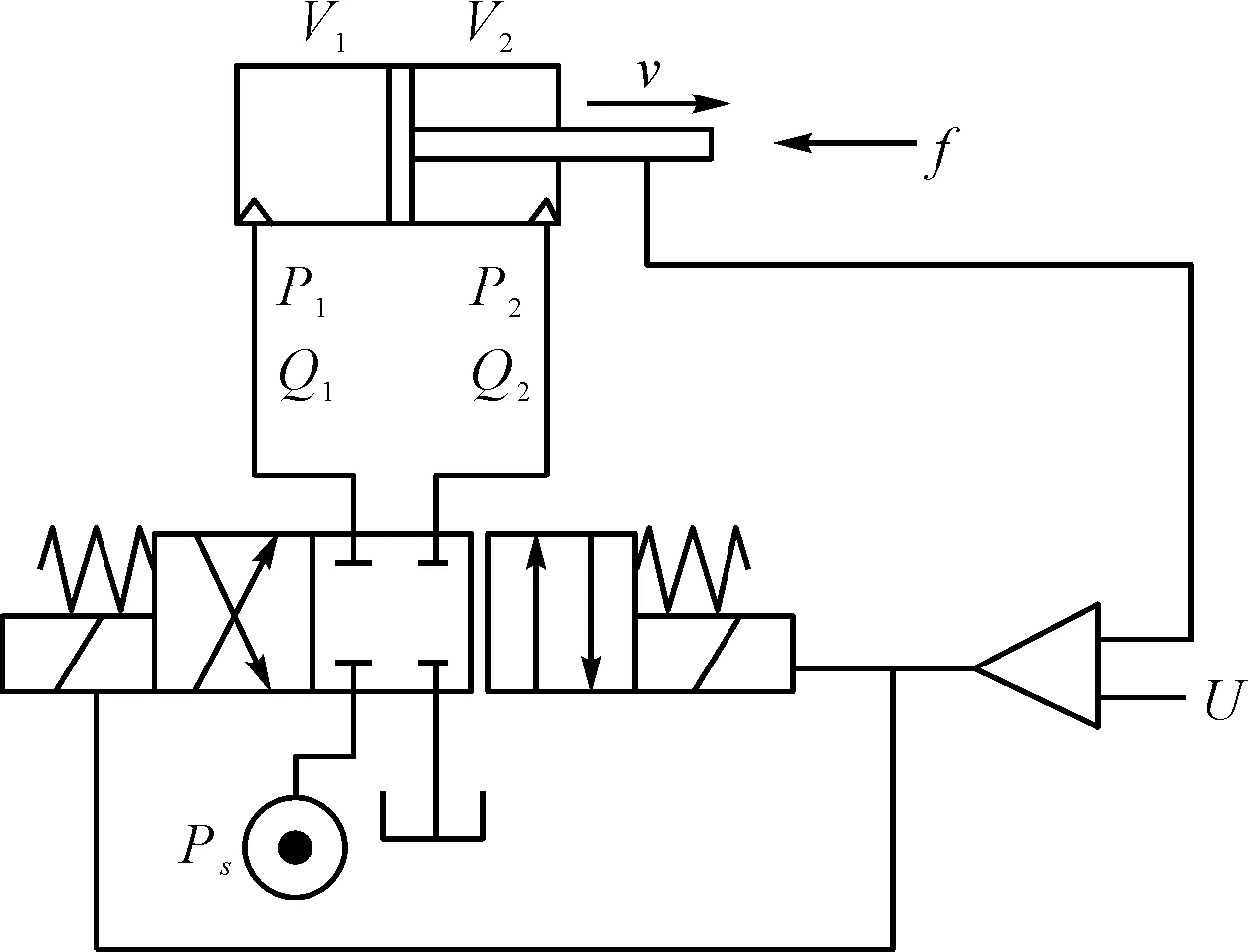
图4 简化后的液压控制系统

对该系统而言,系统的输出信号是活塞杆的运动速度v,控制信号是电磁比例换向阀的电压U,干扰信号是工作负载f,所求的是输出信号对控制信号和干扰信号的传递函数。所根据的是比例换向阀位移方程、滑阀流量方程、液压缸工作腔的流量连续方程和液压缸运动部分的力平衡方程[8]。

2.2.1 比例换向阀位移方程

工程上将比例换向阀视作一个典型的二阶环节,其传递函数为[9]:

(10)

式中:U—比例放大器输入电压信号,V;Ka—比例放大器电器转换增益,A/V;Kv—比例换向阀增益,m/A;ωv—比例换向阀相频宽,rad/s;ζv—比例方向阀的阻尼比。

2.2.2 滑阀的流量方程

在该液压系统下,滑阀的流量方程为:

QLa=Kqxv-KcpL

(11)

式中:Kq—滑阀的流量增益系数,m2/s;Kc—滑阀的流量压力系数,m5/(N·S)。

2.2.3 液压缸工作腔的流量连续方程

液压缸两油腔的流量分别是:

(12)

(13)

式中:Cip，Cep—液压缸内外泄漏系数,m5/(N·S);V1，V2—无杆腔、有杆腔的体积,m3;E—油液等效体积弹性模量,Pa。

定义负载流量为两腔流量的平均值如下:

(14)

由式(12～14)得:

(15)

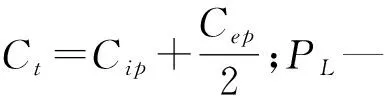
最终得到液压缸的负载流量方程如下:

(16)

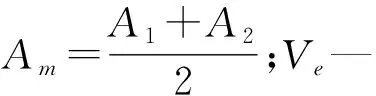
2.2.4 液压缸运动部分力平衡方程

液压缸活塞及滑台的力平衡方程[10]如下:

(17)

式中:M—运动部件总质量,kg;R—黏性摩擦系数,N·s/m;f—外干扰力,N;Ae—液压缸等效活塞面积,m2。

接下来对式(10,11,16,17)进行拉氏变换。并且在该动态系统中,起主导作用的是动力机构环节,比例换向阀和传感器的转折频率更高,所以在该系统工作频率范围内,可以将比例换向阀环节和传感器环节简化成比例环节[11]。

由此,可得系统的传递函数为:

(18)

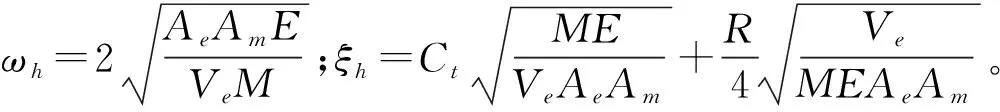
由于该系统输出为液压缸速度,为了反映工作台面的速度变化,笔者用式(8)对系统输出进行转化,系统输入Vs为期望的工作平台速度。

综上所述,最终可以得到该系统的控制系统方框图,如图5所示。

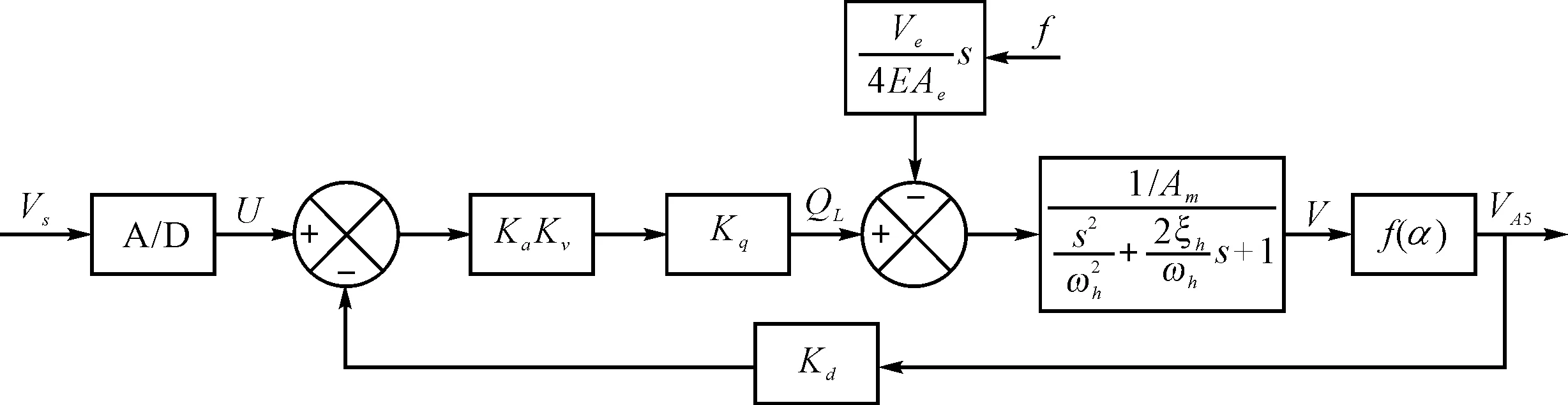
图5 控制系统方框图

2.3 Simulink仿真模型的建立

某型号液压缸缸筒直径为125 mm,活塞杆直径为90 mm,活塞杆工作行程为400 mm;黏性摩擦系数R=2 100 N·s/m,外负载质量M=2 280 kg,系统供油压力Ps=5 MPa,油液密度ρ=900 kg/m3,油液等效体积弹性模量E=0.7×109N/m2,节流阀流量系数Cq=0.6,速度传感器增益Kd=3.8,期望的工作平台速度为0.1 m/s。

笔者将数据代入上述公式中,可计算出仿真所需的参数;采用MATLAB中的组件Simulink分析系统的动态特性,由于Simulink包含了众多的功能模块,每个功能模块下又包含许多子模块,笔者在系统最后添加MATLABFunction模块,并编写程序将式(8)写入,将系统输出转化为工作平台的速度。

2.4 传统PID控制器

为了在动态分析中避免系统不稳定,进一步优化系统的性能,笔者在系统中使用PID控制器和反馈补偿复合校正,可采用试凑法、衰减曲线法等方法对比例、积分、微分3项参数进行不断地调整[12],使系统获得更好的响应性能。

最终建立传统PID控制下的Simulink仿真模型如图6所示。

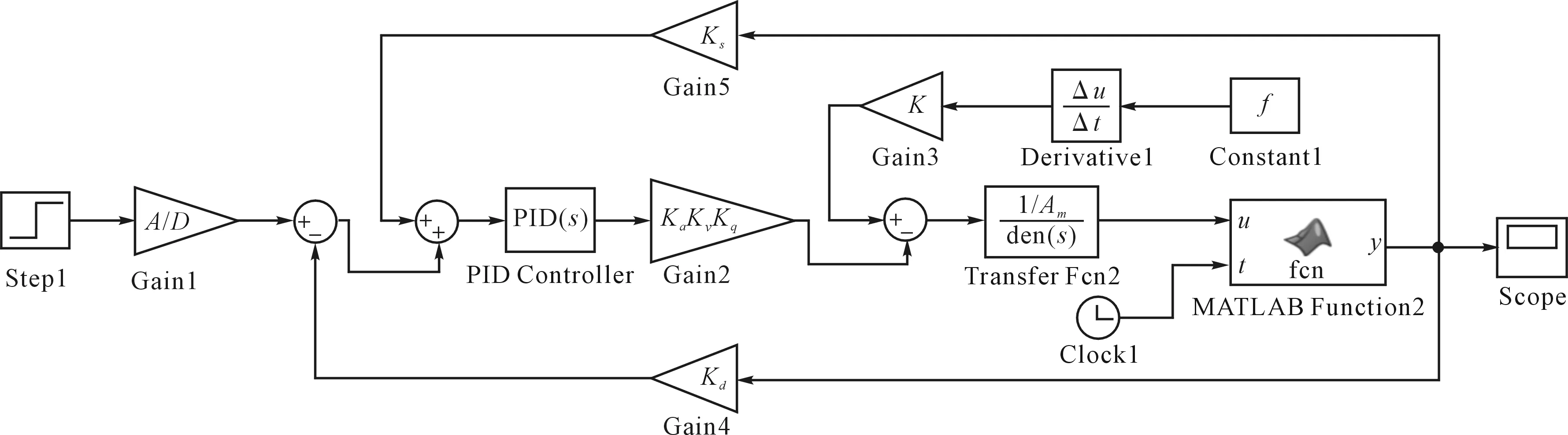
图6 传统PID控制Simulink仿真模型

2.5 模糊PID控制器

模糊PID控制是一种智能控制,在运行过程中不断检测输入e和Δe(其中：e—误差;Δe—误差变化率),根据模糊控制规则对输出比例系数变化量KP、积分系数变化量KI、微分系数变化量KD3个参数进行在线修改,从而使被控对象有良好的动态、静态性能[13-17],输入量和输出量的模糊子集均为{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}。

对该剪叉式高空作业车液压控制系统模糊PID控制器的隶属函数进行设置。其中,e和Δe的隶属函数如图7所示。

KP、KI、KD的隶属函数如图8所示。

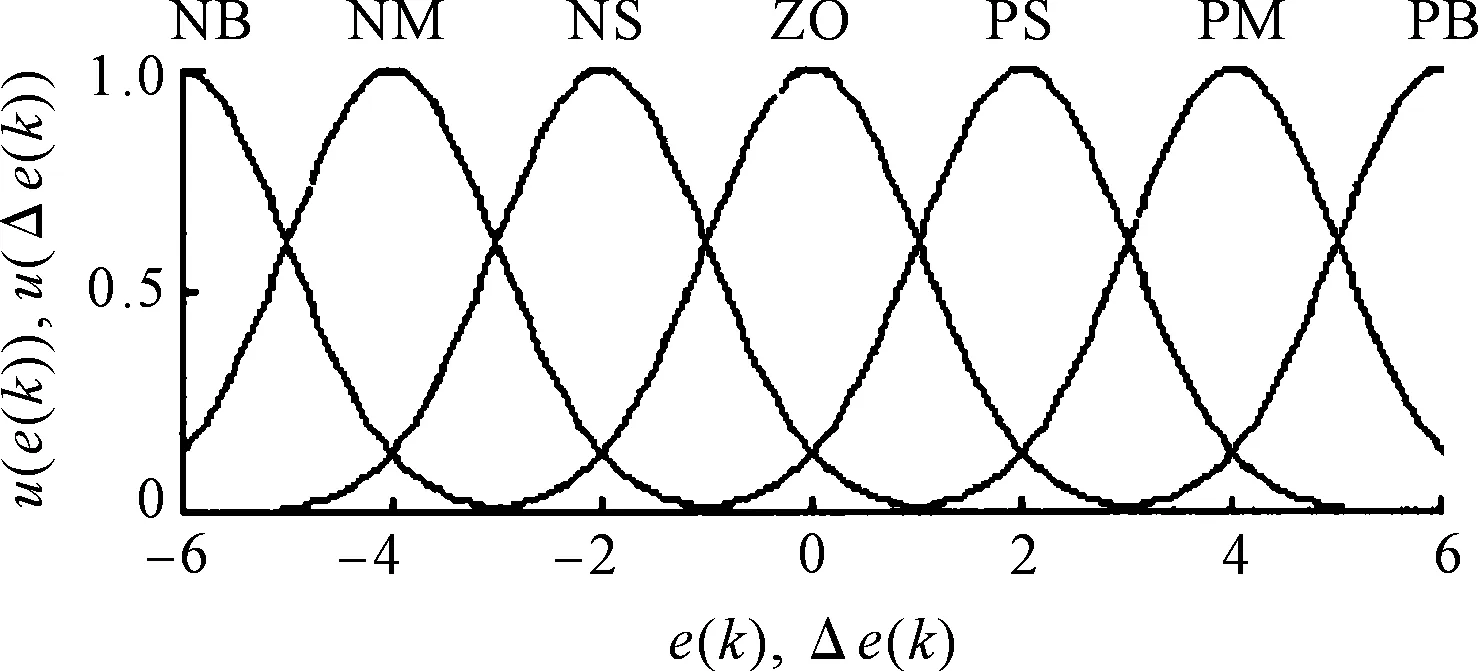
图7 e和Δe的隶属函数

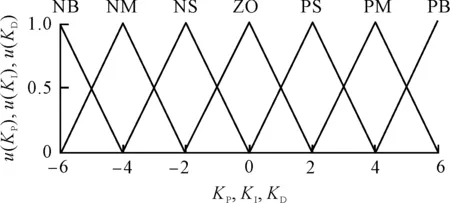
图8 KP、KI、KD的隶属函数

模糊PID控制器的模糊控制规则如表1所示。

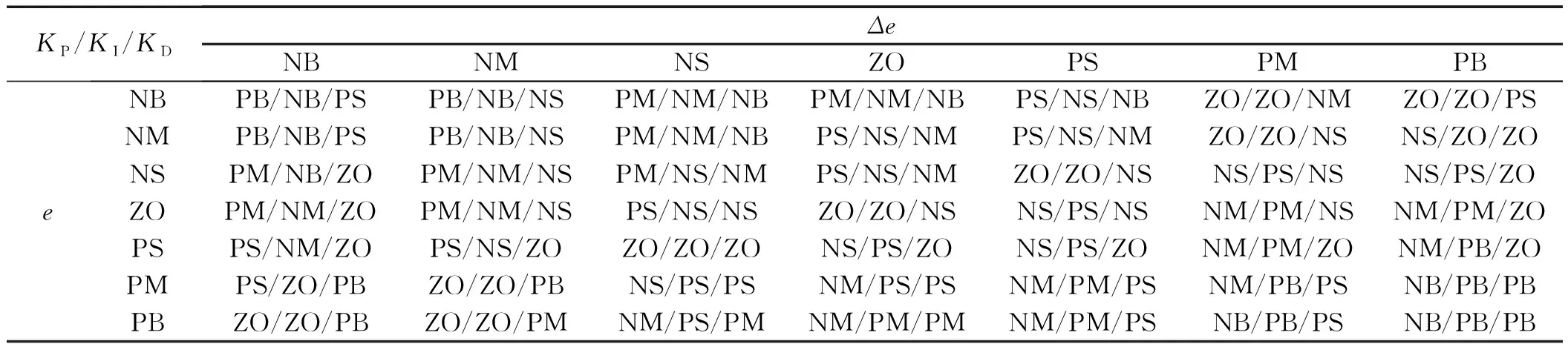
表1 模糊规则控制表

最终建立模糊PID控制的Simulink仿真模型如图9所示。

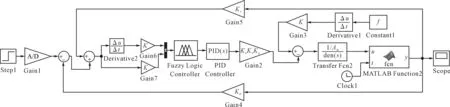
图9 模糊PID控制Simulink仿真模型

3 系统仿真分析

笔者利用仿真软件对剪叉式高空作业平台进行了仿真,得到了启动初期的工作平台速度,如图10所示。

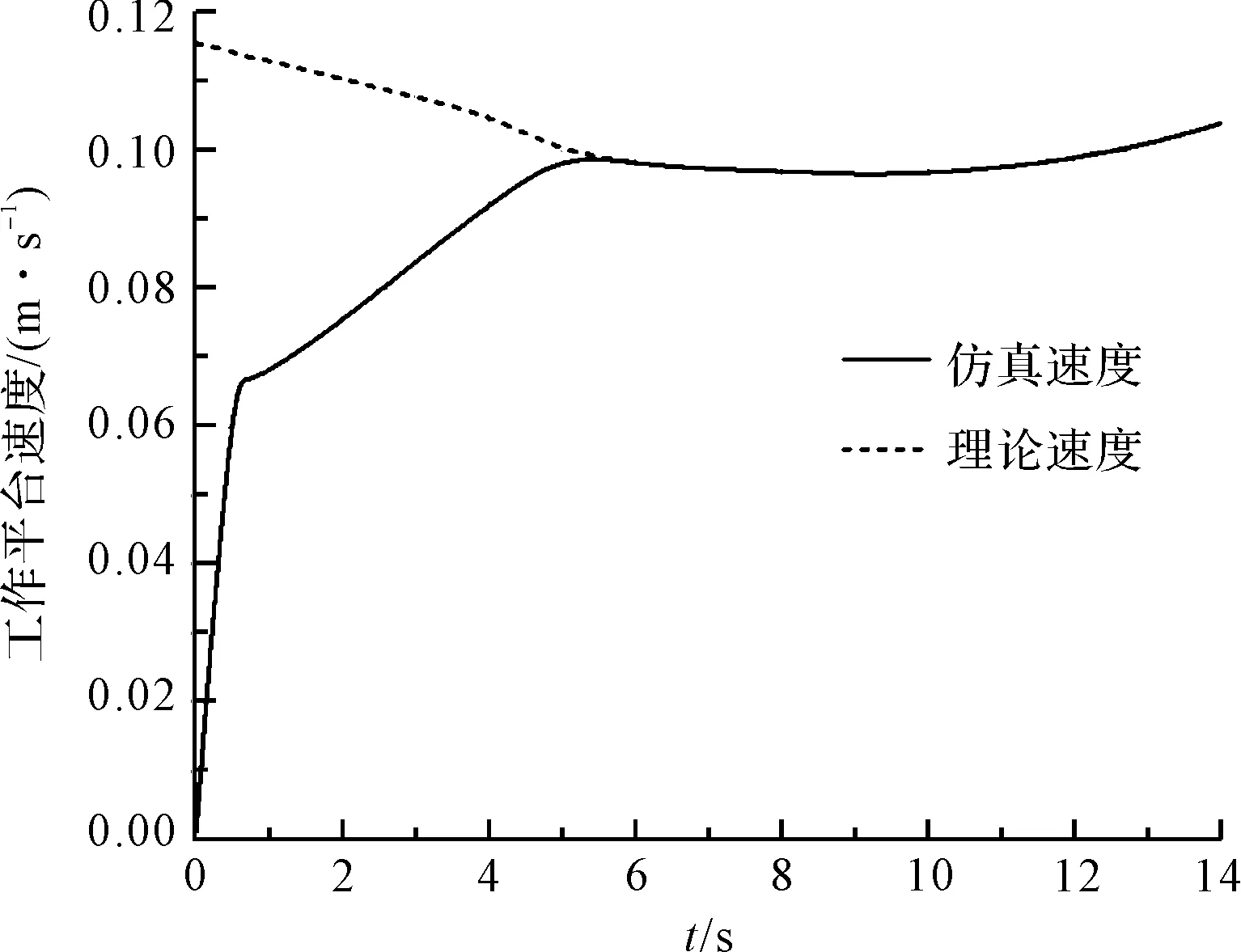
图10 仿真和理论速度对比图

从图10中可以看出:在开始工作的前0.35 s,剪叉式升降平台产生瞬时加速度,是速度上升最快的阶段;在0.35 s～5 s这段时间速度缓慢上升;5 s之后速度按照图2所示规律在变化,在升降平台启动阶段,工作平台需要经过5 s的缓冲时间才能达到理论状态。

为了获得满意的系统性能,笔者对两种PID控制下的Simulink模型进行仿真[18],并得到了系统的输出,如图11所示。

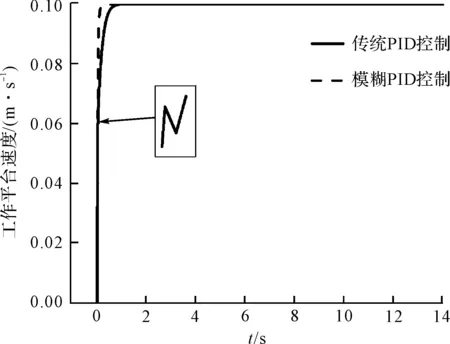
图11 传统PID和模糊PID控制系统输出

从图11中可以看出:模糊PID控制比传统PID控制系统进入稳态的时间更早(约为0.5 s),在保证系统响应快速性的前提下,提高了系统的平稳性,且没有超调,输出的结果符合输入的期望值;

在传统PID控制下,工作平台速度在前0.3 s内有一个明显的抖动,造成这种现象主要是因为传统PID算法中的3个参数都是定值,不能跟随系统的变化而进行自我调整,而模糊PID则很好地解决了这个问题,有效地消除了工作台的振动,由此说明模糊PID控制更适用于对该剪叉式升降平台的控制。

4 结束语

笔者针对某五层剪叉式升降平台,首先用速度瞬心法建立了工作平台的速度函数;其次对工作平台的起升速度控制系统进行了数学建模;最后用Simulink搭建起升速度的控制系统模型,并对传统PID控制和模糊PID控制性能进行了分析和比较。

研究结果表明:

(1)模糊PID能自动调整PID参数,提高了控制系统对环境变化的适应能力;

(2)与传统PID控制相比,模糊PID控制有更好的响应性能,无超调现象,并且消除了系统起升阶段的振动,使工作平台速度快速地稳定在期望值;

(3)通过仿真分析,验证了系统可以实现使工作平台速度快速稳定的目的。

笔者通过模拟建立的数学模型,确定了结构或控制参数的调整范围,其作为实际系统调试的依据,缩短了调试时间,对剪叉式高空作业车液压控制系统的优化具有参考意义和应用价值。但是,因为实验条件的限制,目前笔者尚无法在剪叉式升降平台上测试该系统的实际工作性能。

在后续的研究中,在实验条件允许的情况下,笔者将对该系统进行实验验证。