基于改进集成多隐层小波极限学习神经网络的滚动轴承故障识别研究*
赵凡超,戴石良,房华伟,张丽敏,刘 伟
(1.广西中烟工业有限责任公司,广西 柳州 535006;2.南华大学 土木工程学院,湖南 衡阳 421001;3.湖南核三力技术工程有限公司,湖南 衡阳 421001)
0 引 言
滚动轴承是旋转机械的重要零部件之一,常工作在高速重载工况下,很容易出现故障,因此,及时对滚动轴承故障进行识别具有重要意义[1]。
目前,基于“人工特征提取-人工特征选择-浅层模式识别”的滚动轴承故障诊断方法研究较多。其中,JIANG H K等[2]利用改进集合经验模态分解和多小波包对轴承进行了故障诊断;LEI Y G等[3]利用多种经验模态分解方法对轴承进行了故障诊断。然而现场采集到的振动信号很容易受环境噪声干扰,具有一定的非线性和非平稳性[4],传统的轴承故障诊断方法受主观影响较大,故障特征难以有效提取[5]。
为克服传统轴承故障诊断方法的缺陷,李可等[6]提出了基于极限学习自编码器(extreme learning auto-encoder,ELAE)的轴承故障诊断方法,ELAE将极限学习机(extreme learning machine,ELM)[7]与自编码器(auto-encoder,AE)[8]结合,兼具AE与ELM的优势。
但ELAE为全连接网络,所需要学习的参数较多,训练时间较长,受噪声影响较大;且ELAE一般使用sigmoid激活函数,不能逼近L2(Rn)空间中的任意函数,泛化能力较弱[9];同时,使用单一的网络进行识别泛化能力差。此外,文献[10,11]的研究结果表明:滚动轴承振动信号的噪声会严重降低网络的故障识别率,因此有必要对采集到的轴承振动信号进行降噪前处理。
传统的小波分析降噪方法通过对振动的信号频谱进行二进制分割,从而将信号分解到不同频带,但其缺乏自适应性[12,13];经验模态分解(empirical mode decomposition,EMD)及其变体缺乏严格的理论基础,且存在模态混叠和端点效应等缺陷[14,15]。
本文针对上述研究的缺陷,提出一种改进集成多隐层小波极限学习神经网络的滚动轴承故障识别方法。
1 谱分割小波变换
谱分割小波变换(spectral segmentation wavelet transform,SSWT)是对轴承振动信号的频谱边界进行有效检测和分割,然后建立小波滤波器提取相应的调幅-调频成分,从而将信号分解为若干个本征模态函数(intrinsic modal functions,IMFs)之和。本文提出一种新的频谱分割方法,即考虑频谱形状,使用最大值滤波器的包络寻找主频值,并采取如下准则筛选有效的频率峰值:
准则1。包络平顶频谱宽度要大于统计滤波器尺寸;
准则2。有效包络平顶不能出现在信号频谱的下降趋势段;
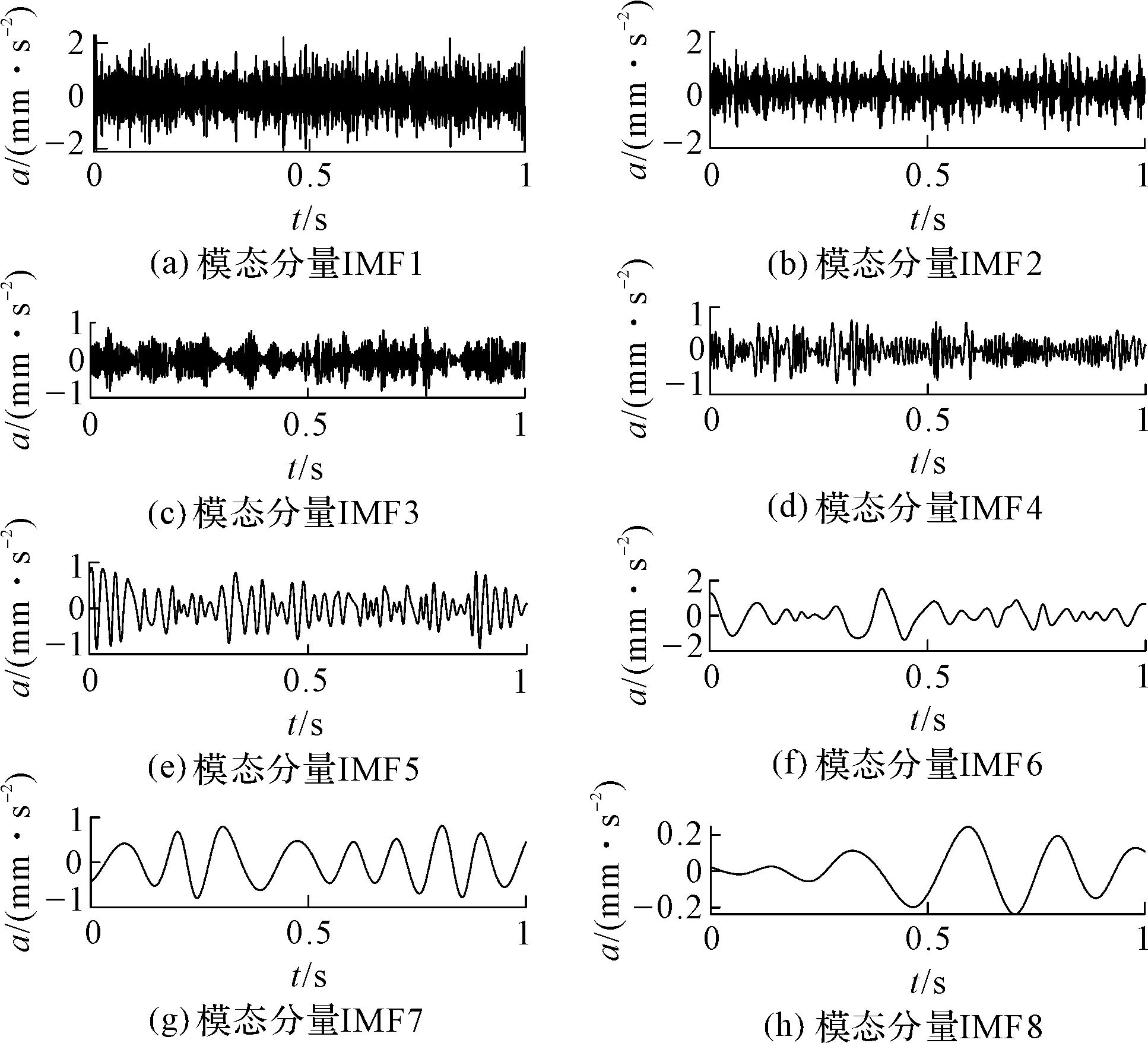
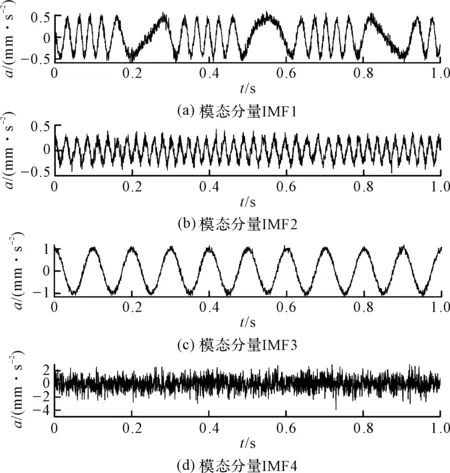
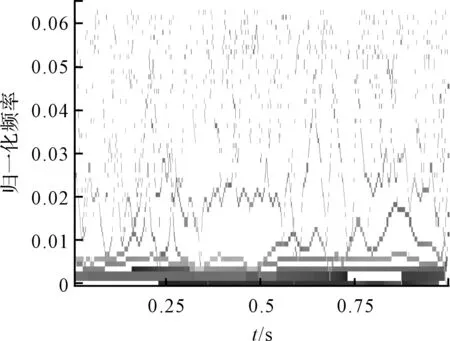
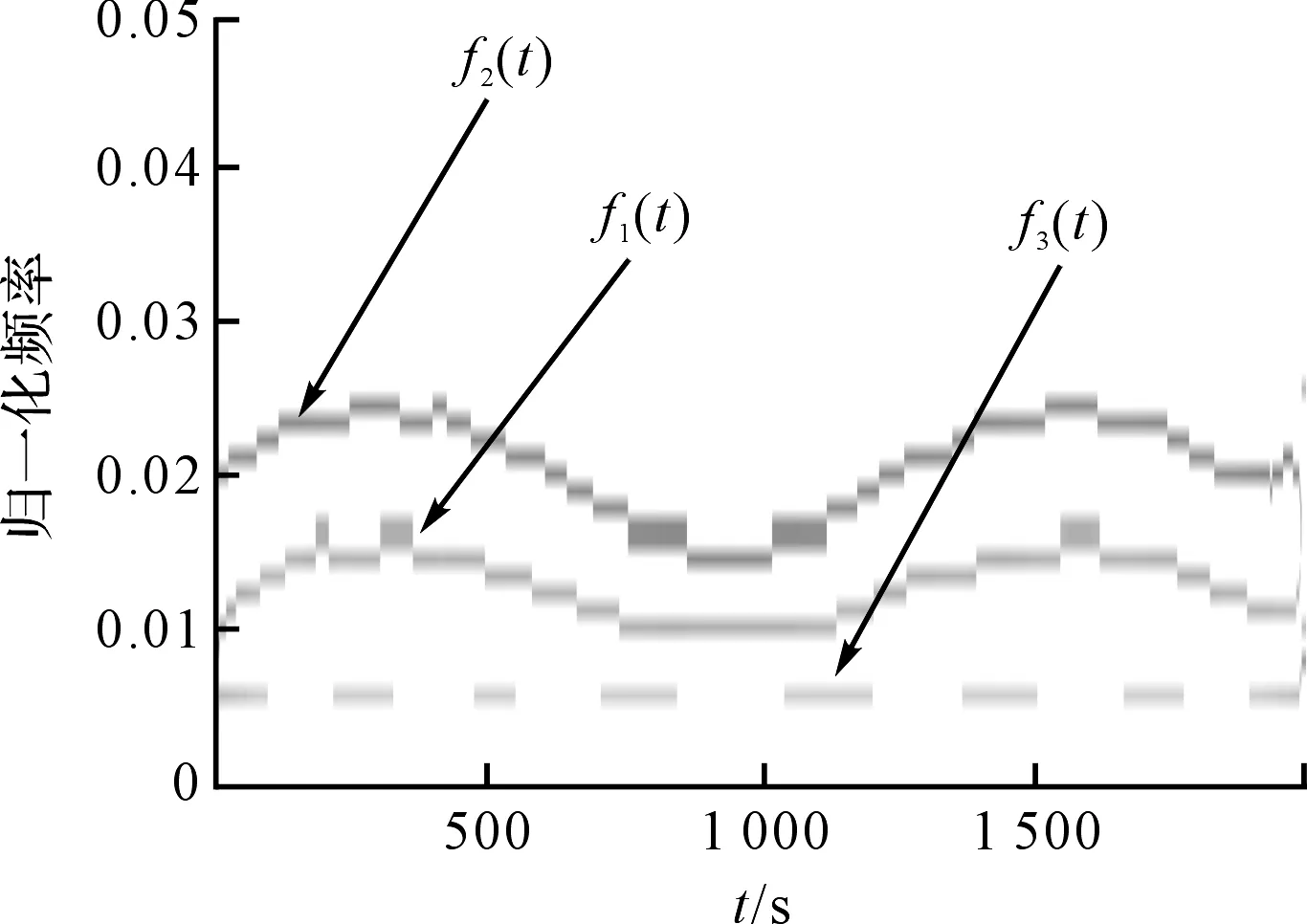
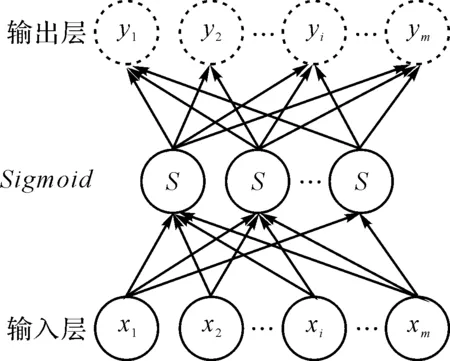
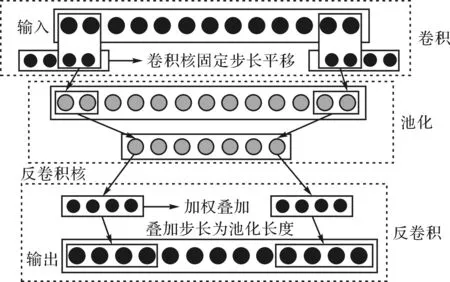
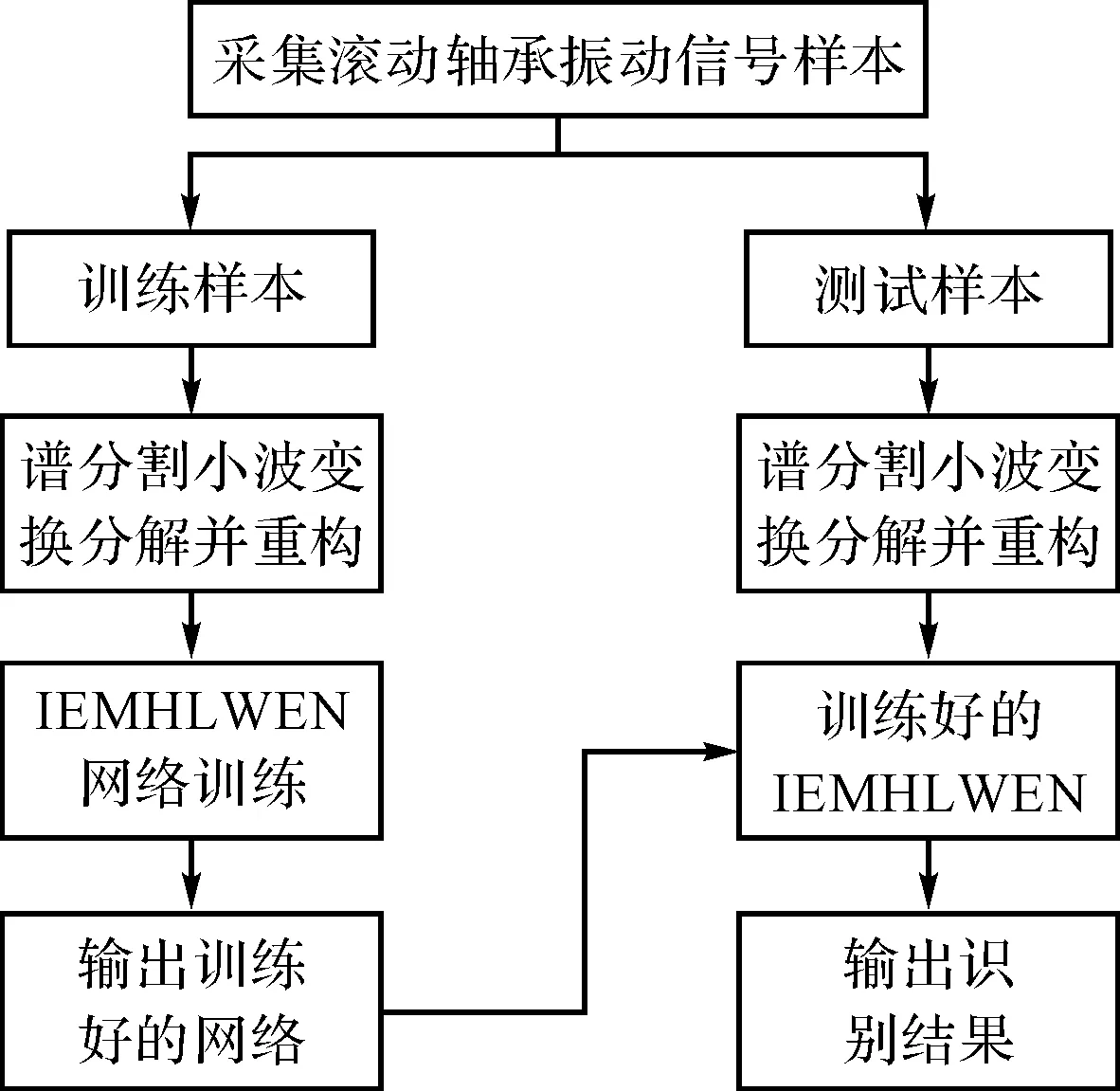
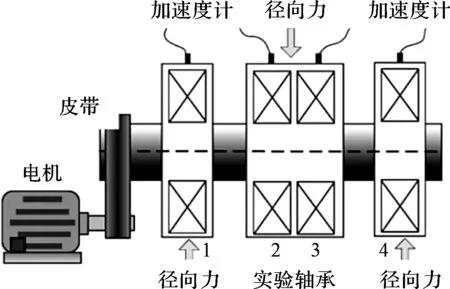
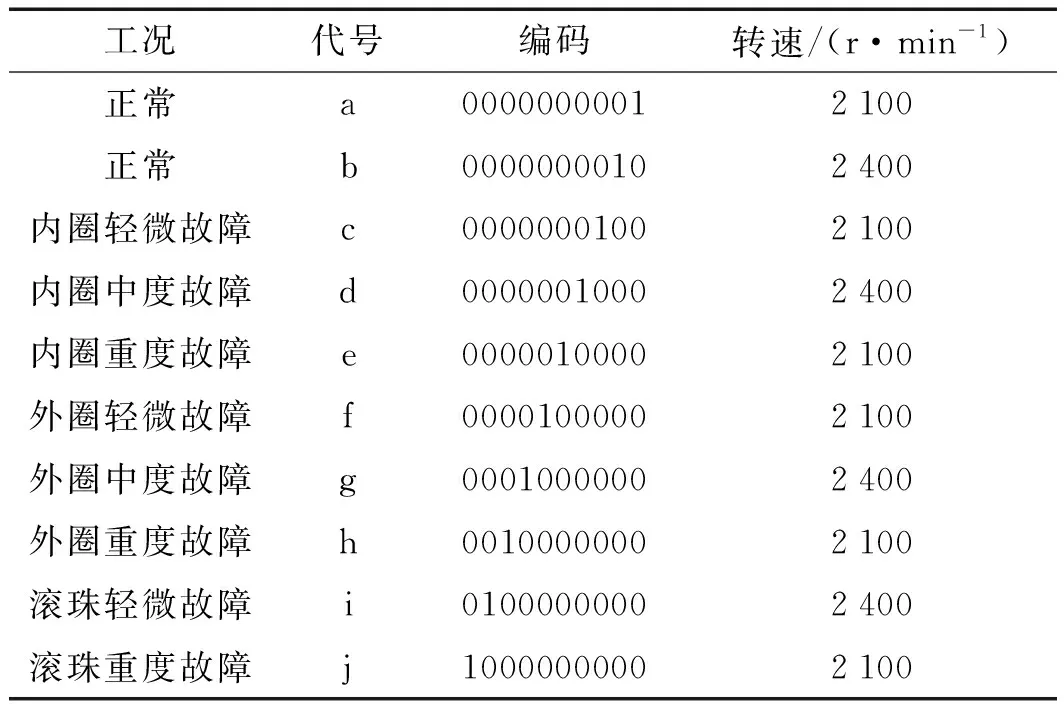
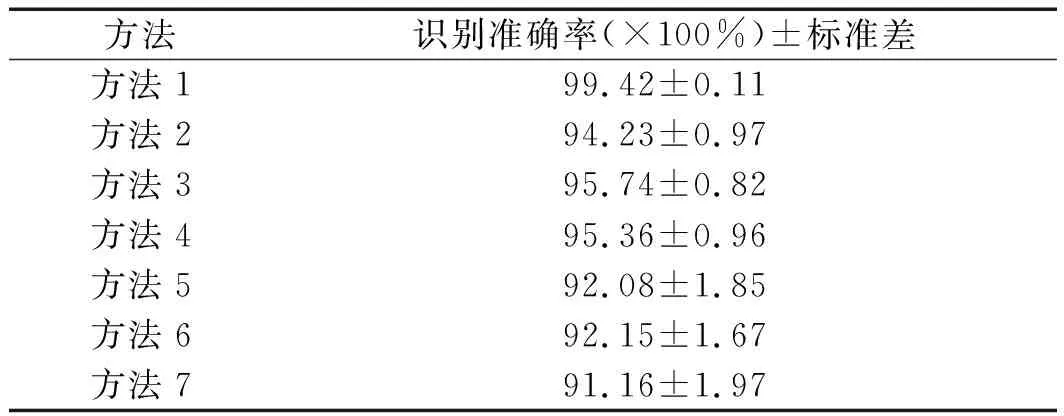
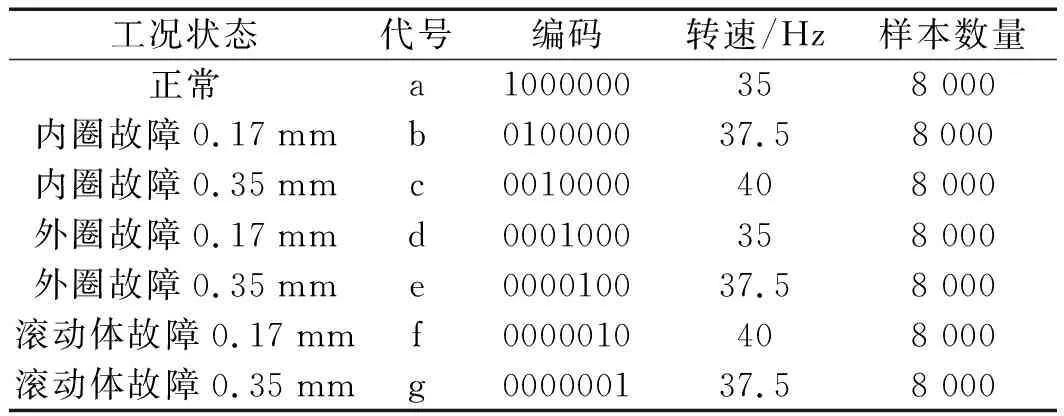
准则3。把包络的局部极大值按降序排列,(M1≥M2≥…≥MM,包括0和π),取MM+a(M1-MM)为阈值(其中:a—相对振幅比,0 (1) (2) 重建公式如下: (3) 式中:*—卷积操作。 信号f(t)可被分解为: (4) (5) 其中:k=(1,2,…,N-1)。 采用仿真信号f(t)进行分析,如下: (6) 式中:f3(t)—余弦信号;f1(t)—调频信号;f2(t)—调频信号;w—白噪声。 笔者采用完备集合模态分解(complementary ensemble empirical mode decomposition,CEEMD)对f(t)进行分解,分解结果如图1所示。 图1 CEEMD分解结果 由图1可知,CEEMD产生了严重的模态混叠效应。 笔者采用谱分割小波变换对f(t)进行分解,分解的结果如图2所示。 图2 谱分割小波变换分解结果 由图2可知,谱分割小波变换能准确地分解仿真信号,对噪声鲁棒性较强。其中,所分解出的模态分量IMF1、模态分量IMF2、模态分量IMF2分别对应于f1(t)、f2(t)和f3(t)。 笔者取与原信号相关性较强的前3层进行重构,CEEMD时频谱如图3所示。 图3 CEEMD时频谱图 由图3可知,CEEMD时频谱杂乱,模态混叠严重。 谱分割小波变换时频谱图如图4所示。 图4 谱分割小波变换时频谱图 由图4可知,谱分割小波变换时频谱能较为准确地分解仿真信号,对噪声鲁棒性较强。 ELAE为3层神经网络,结构如图5所示。 图5 标准ELAE结构图 图5中,输入层神经元个数和输出层神经元个数均为m,隐层神经元个数为L。ELAE的第一步是将输入数据x通过sigmoid激活函数变换为隐层特征向量h=[h1,h2,…,hL]T: h=sigmoid(Wx+b) (7) 式中:W—输入层到隐层的权值向量;b—偏置向量。 ELAE的输出为: y=hTβ (8) 式中:β—隐含层到输出层的输出权重向量。 ELAE的优化函数可以表示为: (9) 式中:β—隐层输出权重。 对于维度压缩,β可以转化为: (10) 式中:H—隐层映射矩阵;I—单位矩阵;C—常数。 但ELAE为全连接网络,训练速度慢,且易产生过拟合,受噪声影响较大,而卷积神经网络(convolutional neural networks,CNN)的局部连接特性可有效降低网络的过拟合;又小波函数具有一定的时频局部化能力,因此,使用小波激活函数代替ELAE的sigmoid函数,具有更优异的特征提取和表示的性能。 因此,笔者将小波和CNN的优势结合,构造改进小波极限学习神经网络(improved wavelet ELM network,IWEN),如图6所示。 图6 IWEN结构图 设IWEN的输入为x,则隐层第k个节点输出如下: hk=ψ[(x*Wk-ck)./ak] (11) (12) 式中:ψ—高斯小波;Wk—卷积核权重矩阵;ak—小波节点的尺度向量;ck—小波节点的平移向量;*—卷积符号;./—按元素相除符号。 IWEN的输出如下: (13) 改进多隐层小波极限学习神经网络堆叠多个IWEN,能进一步提高网络学习到特征的质量。首先,笔者利用振动信号样本训练第一层IWEN,进而得到第1隐层特征;其次,将第1隐层特征输入第2层IWEN,得到第2隐层特征;以此类推。 为克服单一深层网络泛化能力低的缺陷,笔者采用3个具有不同小波激活函数的改进多隐层小波极限学习神经网络的集成。 3种不同的小波激活函数如表1所示。 表1中,笔者利用3个不同小波函数的IDEN对滚动轴承故障进行识别,最后的输出结果采用文献[18]提出的加权平均方法。 表1 不同小波激活函数的方程 综上,采用该方法的轴承故障识别步骤如下: (1)采集滚动轴承不同工况的振动信号样本,随机选取80%作为训练样本,其余为测试样本; (2)对信号样本进行谱分割小波变换,得到IMFs,然后利用峭度评价指标对IMFs进行重建; (3)将重构的训练样本输入IEMHLWEN进行训练; (4)使用测试样本对训练好的模型进行测试。 故障识别流程图如图7所示。 图7 本文方法故障识别流程图 为验证本文算法的可行性和有效性,笔者进行实验验证。试验台如图8所示。 图8 本文轴承故障诊断试验台 试验台由交流电动机、加速度计、转轴、测试轴承等组成。其中,轴承型号为SKF6205,采样频率设置为10 kHz;采用电火花加工技术对轴承的外圈、内圈和滚动体分别设置不同程度的损伤:0.18 mm(轻度损伤),0.36 mm(中度损伤)和0.50 mm(重度损伤)。 限于文章篇幅,笔者取10种不同滚动轴承运行工况,如表2所示。 表2 10种滚动轴承运行工况 最后得到每种工况下8 000个样本,每个样本1 024个采样。 10种电机轴承运行工况的时域图如图9所示。 图9 滚动轴承10种工况时域图 由图9可知,故障信号受噪声干扰严重,难以直接从时域图中对滚动轴承的故障类型及程度进行有效区分。 笔者以轴承外圈中度故障振动信号为例,分别采用谱分割小波变换和CEEMD对其进行分解,分解结果如图(10,11)所示。 图10 谱分割小波变换分解结果 图11 CEEMD分解结果 根据峭度指标,笔者选择峭度值较大的前3个分量进行重构,如图12所示。 图12 CEEMD和谱分割小波变换重构结果 笔者以均方根误差(RMSE)和信噪比(SNR)衡量重构降噪效果,RMSE越小且SNR越高,表明降噪效果越好。 经计算,CEEMD重构信号SNR和RMSE分别为1.79和3.789,谱分割小波变换重构信号的SNR和RMSE分别为6.68和1.081。该结果说明,谱分割小波变换方法很好地实现了重构降噪。 随后,笔者对降噪后的轴承振动信号进行相应的时频变换,如图(13,14)所示。 图13 CEEMD重构信号时频谱 图14 谱分割小波变换重构信号时频谱 为验证本文方法的有效性,笔者采用不同模型进行分析对比,每个深层网络结构均为1024-512-256-128-64-32-10。 方法1。SSWT-IEMHLWEN; 方法2。CEEMD-IEMHLWEN; 方法3。VMD-IEMHLWEN; 方法4。SSWT-IMHLWEN(改进多隐层小波极限学习神经网络,Morlet小波激活函数); 方法5。SSWT-DAE(深层自编码器); 方法6。SSWT-DBN(深层信念网络); 方法7。信号不经处理直接输入IEMHLWEN。 这几种方法10次实验平均故障识别率与标准差如表3所示。 表3 不同方法的平均故障识别结果 由表3可知:本文所提方法具有更高的故障识别准确率(99.42%)和更小的标准差(0.11);基于CEEMD和VMD信号分解前处理的方法均存在一定程度的模态混叠现象,导致难以为IEMHLWEN提供较为优异的训练样本,轴承故障识别率较低;若直接将带噪声振动信号输入IEMHLWEN,受噪声影响,故障识别率仅91.16%,远低于本文方法,验证了分解降噪前处理的有效性; 同时,由表3可知,将多个深层网络进行集成的识别结果要优于单一的深层网络,这是因为单一深层网络泛化能力低,进一步验证了集成学习的优势。 训练集和测试集的样本比例对模型的故障识别率有一定影响,若训练集样本比例过低,则会引起IEMHLWEN欠拟合;若训练集样本比例过高,则会引起IEMHLWEN过拟合。可见,欠拟合和过拟合均会影响IEMHLWEN的故障识别准确率。 训练集样本占比60%~90%时,本文模型的故障识别准确率如图15所示。 图15 不同比例的训练集对故障识别准确率的影响 由图15可知,在训练集样本占比60%~80%时,本文模型的故障识别率随训练集样本所占比例的增加而增加,当超过80%时,工况识别率已不再上升,故笔者选取80%的训练集样本。 为进一步验证IEMHLWEN方法的有效性,笔者以轴承故障诊断领域的Benchmark数据集:西储大学CWRU轴承数据集[19]为对象。 CWRU轴承数据集利用电火花技术在轴承内圈、滚动体和外圈上引入单点损伤,损伤直径分别为0.17 mm、0.35 mm、0.53 mm,使用安装在驱动端且转速为1 720 r/min~1 797 r/min,以及采样频率为12 kHz和48 kHz时的电机振动数据,生成数据集。 CWRU轴承实验台如图16所示。 图16 CWRU数据集实验台 限于计算资源,笔者从数据集中选取7种不同的轴承故障工况,如表4所示。 表4 7种滚动轴承故障工况 为进一步证明IEMHLWEN方法的优势,笔者采用轴承故障诊断领域的2个Benchmark方法进行对比分析,分别为:文献[20]提出的追踪深层小波自动编码器(tracking deep wavelet auto-encoder,TDWAE)和文献[21]提出的集成深层自动编码器(ensemble deep auto-encoders,EDAE);3种方法的输入均为1 024维信号样本,各网络结构均为1024-512-256-128-64-32-7。 笔者共进行10次试验,3种方法的平均识别精度、F1值、平均训练用时和平均测试用时,如表5所示。 表5 不同方法的识别结果 F1值计算如下: (14) 式中:P,Q—准确率和召回率。 其中,F1在[0,1]之间,0代表最差,1代表最好。 由表5可知,IEMHLWEN网络具有更高的识别准确率(99.08%)和更大的F1值(0.969),能较为稳定地识别出滚动轴承的不同故障类型及故障程度。由于信号前处理的原因,训练用时高于TDWAE,但低于EDAE。由于EDAE是多个DAE进行集成学习,训练用时较多,但3种方法单个样本的平均测试时间均较低。 为解决滚动轴承振动信号存在难以提取和其工况状态难以辨识的问题,本文提出了一种基于改进集成多隐层小波极限学习神经网络的滚动轴承故障识别方法。采用该方法得到的滚动轴承故障识别准确率达到了99.42%,标准差为0.11。 主要研究结论如下: (1)提出了一种谱分割小波变换振动信号分解方法,对采集到的滚动轴承振动数据的频谱进行分割,频谱分割时考虑频谱形状;并采取阈值准则筛选有效频率峰值,从而自适应划分信号频段进而自动确定分解模态数,能较准确地分解仿真信号和实际滚动轴承振动信号,对噪声鲁棒性较强,为后续IEMHLWEN自动特征提取和故障识别提供优秀的训练样本; (2)提出的IEMHLWEN将CNN的局部连接特性和ELM结合,可有效降低网络的过拟合,提高了滚动轴承故障识别准确率,且将单一深层网络模型进行集成,获得了比单一深层模型更好的学习效果。 在后续的研究中,笔者将进一步研究谱分割小波变换的更为有效的频谱分割算法,以及IEMHLWEN更有效的训练算法。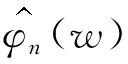
2 改进集成多隐层小波极限学习神经网络
2.1 改进小波极限学习神经网络
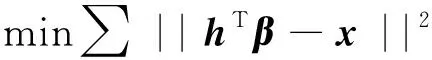
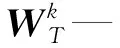
2.2 集成学习

3 实验验证
3.1 实验数据
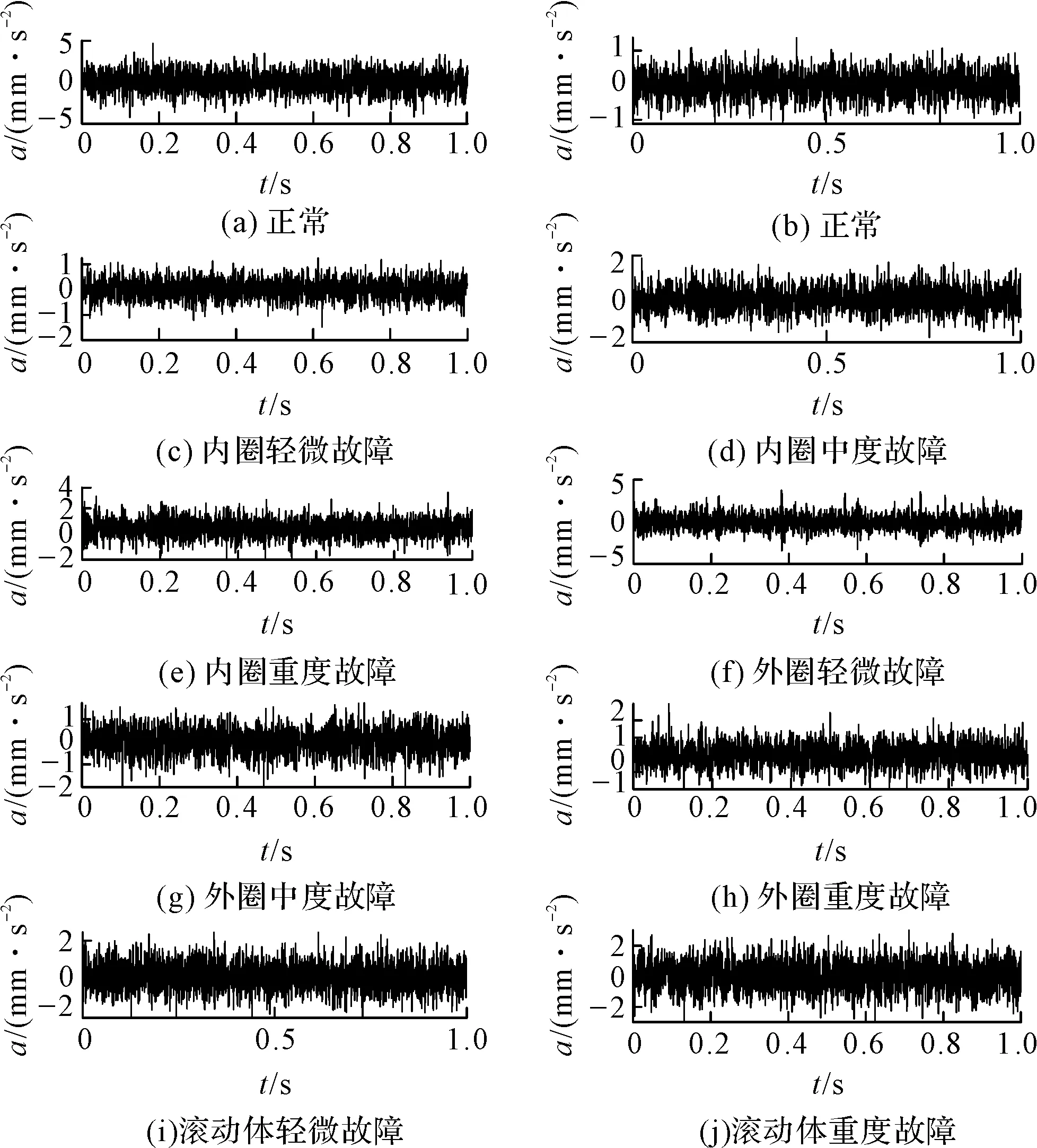
3.2 实际信号分解


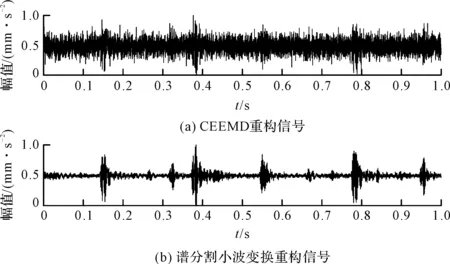
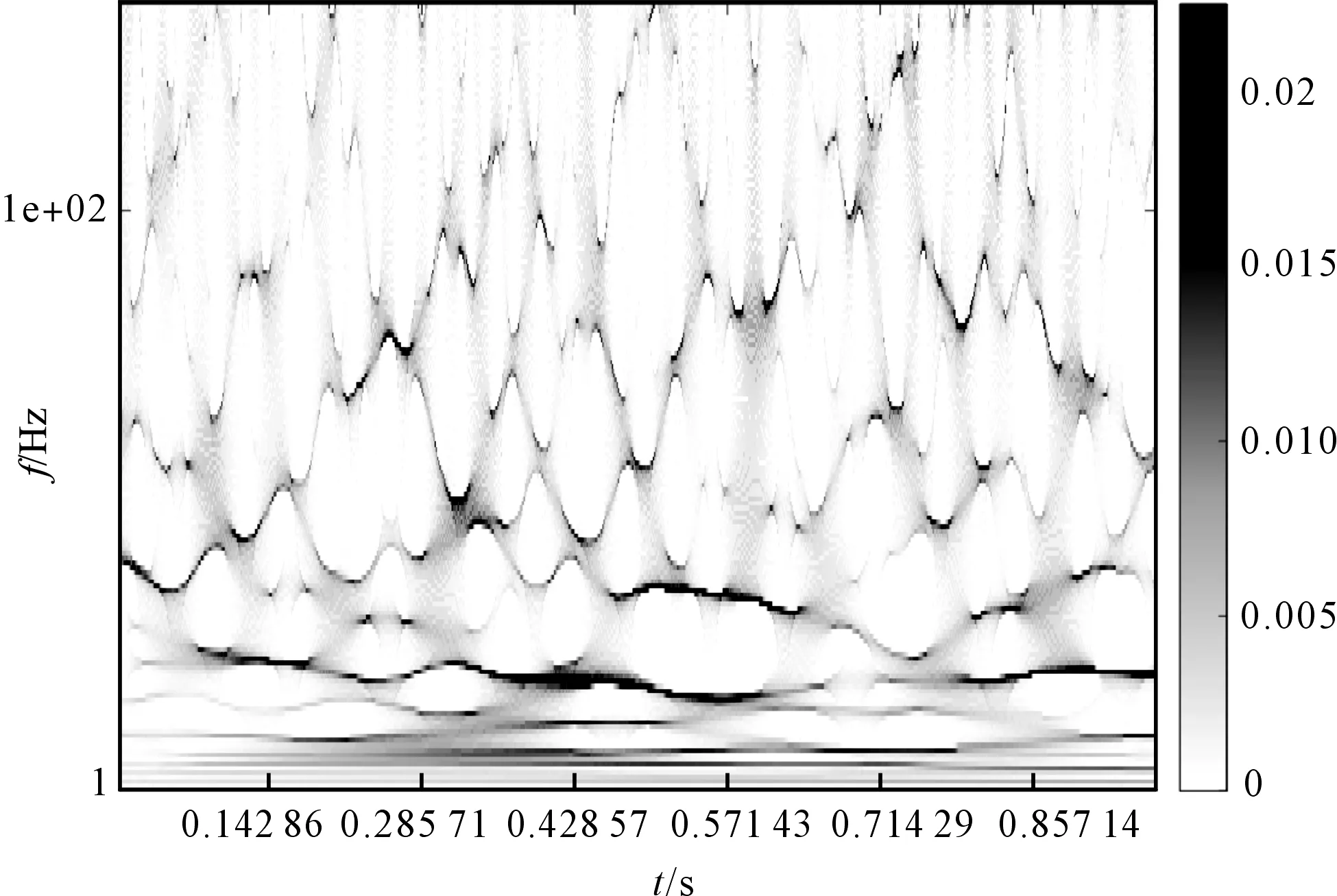
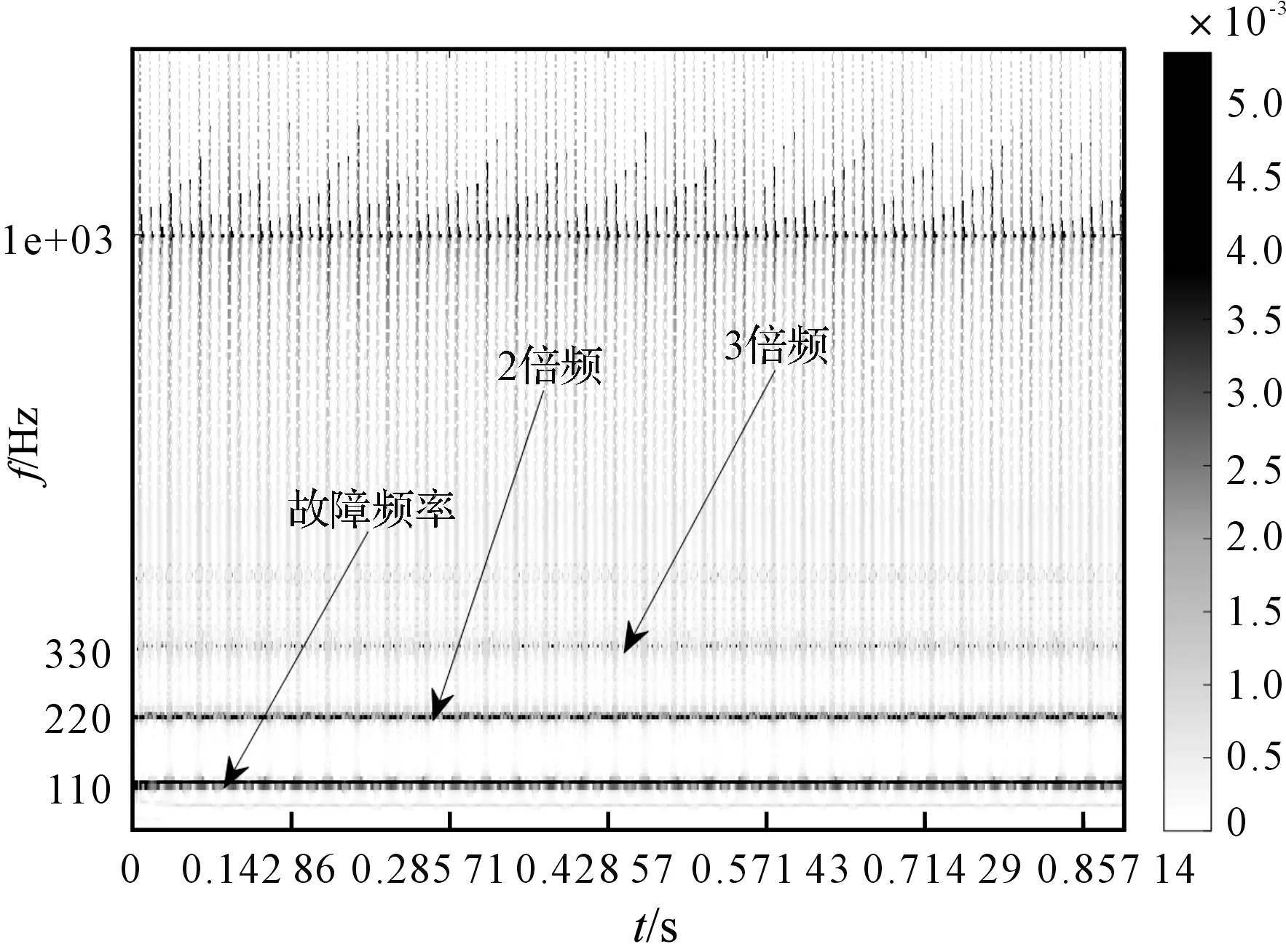
3.3 故障识别与分析
3.4 不同比例的训练集对故障识别准确率的影响

3.5 CWRU数据集下不同方法的轴承故障识别率


4 结束语

