基于MSST和双通道CNN技术的变转速轴承故障诊断研究*

张 冰,姜培刚,林天然

(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)

0 引 言

随着计算机和互联网技术的迅速发展,旋转机械状态检测信息已经迎来“大数据”时代[1]。

滚动轴承在旋转机械设备中起着至关重要的作用,其一旦发生故障将会影响到机器的整体性能,严重情况下甚至会导致机器停止运行[2]。在实际工业应用中,由于生产需要或现场工作环境变化,机械设备的转速或负载条件经常发生变化,滚动轴承监测信号经常表现为非平稳性信号,如何有效进行非平稳信号故障特征提取及诊断已成为当下众多学者的研究热点。

时频分析技术如短时傅里叶变换(STFT)[3]、小波变换(WT)[4]和同步压缩变换(SST)[5]等广泛用于非平稳信号处理和故障特征提取。过去几十年间,这些方法在机械故障诊断领域的应用已逐渐成熟,并取得了很大的成功。但受限于海森堡测不准原理,这些方法仅适用于分析准平稳信号,或具有缓慢时变特征的信号[6],在处理因变工况引起的非线性、非稳态状态监测信号方面仍存在较大的局限性。为了解决该问题,于刚等人[7]最近提出了一种多次同步压缩变换(MSST)技术,该方法通过一种迭代重分配技术对信号的时频分量能量分布进行多次同步压缩变换(SST),以提高非稳态信号时频分布中特征信号分量的能量集中度,分析结果表明,该方法可以有效处理强时变信号并准确计算出变速轴承故障的时频图谱。本研究将采用该方法对变转速工况下滚动轴承振动信号进行分析和实验。

随着计算机技术及人工智能算法的不断发展深化,深度学习作为一种智能方法已被成功用于语音识别、图像处理和人脸识别等领域,并取得了显著的成果[8]。其中,卷积神经网络(CNN)由于其强大的自主学习和特征提取能力,已被国内外诸多专家学者用于机械故障诊断领域。例如,YUAN J H等人[9]通过对滚动轴承的振动信号进行连续小波变换获得时频分布图,然后结合CNN网络对轴承故障进行分类识别,实现了滚动轴承的故障智能诊断;GUO X等人[10]提出了一种分层学习速率自适应的深度卷积神经网络,并将其用于轴承故障诊断及故障严重度的分类识别;ZHANG W等人[11]提出了一种基于一维卷积神经网络的轴承故障诊断方法,通过将预处理过后的轴承振动信号以“端到端”的形式直接输入到模型中,对其进行了故障识别,取得了较好的诊断结果。

上述文献采用的CNN方法及取得的智能诊断结果为本次工作提供了很好的指导意义,但以上方法都是通过卷积神经网络对线性、稳态信号进行信号特征提取及故障识别,而实际工程应用中的轴承故障信号通常具有非线性、非稳态特征,利用改进的CNN算法开展变工况轴承智能诊断研究具有很大的工程应用价值和现实意义。

有鉴于此,笔者提出一种结合多次同步压缩变换和双通道卷积神经网络的混合模型,用于变工况下滚动轴承的故障智能诊断。

1 多次同步压缩变换

多次同步压缩变换是在同步压缩变换(SST)的基础上,采用迭代重分配方法逐步提高时频分布故障特征分量的能量集中度。该方法可以很好地分析处理多分量强时变信号,有效捕捉非平稳信号中各故障分量的时频特性[12]。

对一个多分量非平稳信号s(t),其表述式为:

(1)

式中:K—信号中包含的信号分量个数;Ak(t)—瞬时幅值;φk(t)—该分量的瞬时相位。

同步压缩变换(SST)通过使用频率重新分配算子,来收集信号s(t)在进行短时傅里叶变换G(t,ω)时分散的时频系数,即:

(2)

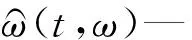
通过SST运算,可以将短时傅里叶变换得到的能量发散时频分布有效压缩到特征时频分量的瞬时频率附近,以获得能量集中的时频分析结果。

多次同步压缩变换(MSST)是在SST基础上,通过多次迭代使得信号时频分量的能量在其瞬时频率附件得到进一步压缩,以获得能量高度集中的时频分布。

多次同步压缩变换表达式为:

(3)

式中:N—总迭代次数。

(4)

式中:φ′(t)—信号s(t)的瞬时相位φ(t)的一阶导数。

通过多次迭代,由式(4)表述的瞬时频率将会越来越接近信号的真实瞬时频率,从而获得强时变信号的高分辨率时频图谱。

2 卷积神经网络

卷积神经网络是一种典型的深度结构前馈神经网络,是深度学习重要的模型之一[13]。卷积神经网络模型主要由卷积层、池化层及全连接层3类结构层组成。

经典LeNet-5[14]模型如图1所示。

图1 LeNet-5网络结构图

该模型包含由卷积层与池化层串联堆叠组成的基础单元模块,并在模型输出端连接两个全连接层,从而组成一个完整的信息提取及模式识别网络模型。

卷积层作为卷积神经网络中最为重要的核心层,其包含多个卷积核(滤波器)[15]。前一层的特征图或特征向量输入到卷积层中,分别与卷积核做卷积运算,并结合激活函数映射出新的特征信息,以作为该层的输出。

其卷积运算代数表达式如下:

(5)

非线性激活函数是卷积神经网络中不可缺少的关键模块,为了防止在反向传播的时候出现梯度爆炸或梯度弥散的情况,CNN模型一般采用ReLU函数作为网络的激活函数,其代数表达式如下:

f(x)=ReLU(x)=max(0,x)

(6)

在卷积层后通常设置池化层来进行降采样操作,对前层输出特征信息进行简化和提炼,其目的是降低维度和从数据中捕获更多的特征信息;同时,也可以在一定程度上降低网络的参数量,防止过拟合,并提高计算速度。

CNN模型通常在中间隐藏层中使用最大池化层,而在输出端使用平均池化层。这样不仅可以减少冗余的参数,同时也能保证有更多有效的特征数据被保留下来,使得网络学习的效果更好。

池化层代数表达式如下:

(7)

式中:Pm—最大池化层的输出矩阵;S—池化层的尺寸。

作为网络的输出层,全连接层是整个卷积神经网络的“分类器”,其作用是将网络学习到的特征信息映射到样本的标记空间。对于多分类问题,CNN模型使用SoftMax函数输出最后分类结果。

全连接层代数表达式如下[16]:

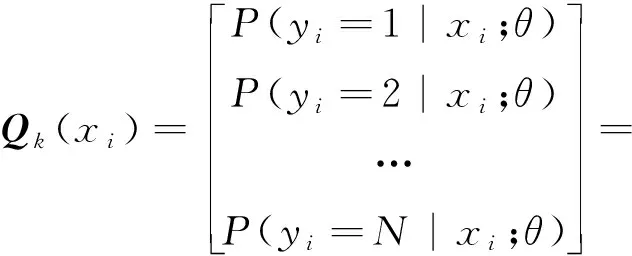
(8)

式中:θ(1),θ(2),…,θ(N)—模型中的参数集合;Qk(xi)—卷积神经网络最终输出结果。

3 基于MSST与TCNN的故障诊断流程和模型结构

3.1 MSST和TCNN模型故障诊断流程

基于MSST与双通道卷积神经网络的变转速轴承故障诊断流程如图2所示。

图2 基于MSST与TCNN的故障诊断流程图

通过该模型的轴承故障智能诊断流程可以划分为三大部分:(1)首先笔者通过峰值保留降采样法[17]对原始数据进行减样处理以减少数据量,然后通过MSST技术获得变速轴承故障信号的时频分布图谱;(2)第二部分将时频分布图谱输入到设计好的双通道深度卷积神经网络(TCNN)进行故障特征提取,通过网络进行监督学习,在训练过程中网络不断调节自身权重,最终输出高准确率的故障识别;(3)第三部分则是通过预留的测试数据集验证模型的故障分类性能。

3.2 TCNN模型结构与参数设定

在提取图像特征时,采用传统的单通道卷积神经网络存在局部特征信息提取不充分的问题。

根据经典CNN模型LeNet-5结构,笔者设计了一种双通道CNN。

基于MSST和TCNN的故障诊断模型结构图如图3所示。

该模型由两条单通道CNN组成,每条通道网络由3个卷积层和池化层交替连接,然后利用Concatenate机制[18]将两条通道提取到的特征信息进行融合,进而得到深层的故障特征信息,最后结合全连接层和Softmax函数输出故障分类结果。

图3 基于MSST和TCNN的故障诊断模型结构图

由于卷积核的大小决定着捕获故障特征信息的范围,较大的卷积核有助于提取全局特征信息,但它会忽略图像的小特征,且需要使用较多参数;而较小的卷积核可以有效提取局部特征,但不利于提取稀疏特征。

因此,经综合考虑,笔者设计了如图3所示的TCNN模型结构。在保持较少参数量的条件下,该模型中通道一与通道二内分别采用2×2和3×3的小卷积核代替大卷积核,这样不仅可以得到更深层的特征信息,提高模型的非线性映射能力,同时也可以减少网络参数,提高其运算速度。

TCNN各通道参数设置如表1所示。

表1 TCNN各通道参数设置

4 基于MSST与TCNN的变转速轴承故障诊断

4.1 轴承故障实验

为验证所提模型的有效性,笔者通过实验室轴承故障模拟实验台采集到的变转速工况下的轴承故障振动信号进行分析。

轴承模拟故障诊断实验台如图4所示。

图4 轴承模拟故障诊断实验台

该实验台主要由变频控制器、转速显示器、变频电机、弹性联轴器、滚动轴承、故障轴承组成。在采集信号的过程中,通过安装在轴承座上的加速度传感器(B&K4370)采集故障轴承信号;采样频率设定为10 kHz,电机转速在9 s内由0 r/min加速至1 500 r/min,即完成一次信号的采集;故障轴承型号为单列滚子轴承(ER-16 k)。

为模拟零部件早期微弱失效在轴承上设置局部故障,同时考虑到轴承上可能出现的故障,该实验被测轴承一共包含5种状态。

测试轴承如图5所示。

图5 测试轴承实物图

轴承故障分别为:①正常;②内圈故障;③外圈故障;④滚动体故障;⑤复合故障(含内圈、外圈和滚动体3种故障)。

故障轴承不同健康状态下的时域波形图如图6所示。

图6 故障轴承不同健康状态下的时域波形图

从原始振动信号时域图上可以看出,本次研究的振动信号呈现加速度状态,符合变转速工况下的运行规律。

由于采集到的变转速振动信号含有冗余信息,且数据量较大,为了提高计算效率和时间,笔者首先采用峰值保持降采样算法,在不丢失信号特征信息情况下降低每一个数据包的数据量,然后通过多次同步压缩变换(MSST)来获得视频图谱。

不同状态下轴承监控信号的时频分布如图7所示。

(a)正常状态

图7分别展示5种轴承不同状态下的时频表示。除了正常状态可以看到转动频率带,其他故障的时频分布都有效地压缩到特征时频分量的瞬时频率附近。

轴承故障样本的数据集如表2所示。

表2 轴承故障样本数据集

由表2中,笔者对每种轴承健康状态进行采集,并通过多次同步压缩变换后,生成300张时频分布图样本,得到共1 500张样本图;把样本以6 ∶2 ∶2的比例划分为训练集、验证集和测试集,并输入TCNN模型进行训练及故障分类。

4.2 TCNN模型训练与分类

笔者通过对初始化的TCNN模型进行10次迭代训练,并观察其学习曲线。

训练和验证精度曲线图如图8所示。

图8 训练和验证精度曲线图

由模型输出训练集和验证集的测试准确度结果可知,当模型经过第5次训练后,其训练和验证损失值迅速收敛至4%以下;在第5次迭代训练后的模型平均验证精度达到99.67%。

通过训练集和验证集的实验结果,验证了文中提出的模型可以准确地对变转速滚动轴承的故障进行诊断识别。

为了验证所提双通道卷积神经网络在变转速轴承故障诊断的有效性和优越性,笔者将双通道卷积神经网络(TCNN)在不同迭代训练次数时得到的诊断准确度,与使用卷积核尺寸为2×2、3×3和5×5的单通道CNN得到的诊断结果进行对比。

不同结构模型平均验证精度如图9所示。

图9 不同结构模型平均验证精度

由图9结果可知,当卷积核尺寸较小时,由于网络能够更容易捕获数据中的微小特征,其对故障特征的提取能力更强,准确率更高;

从图9中也可以看出,采用小卷积核双通道网络可以输出较高且较为稳定的故障分类准确率。

为进一步检验所提模型的鲁棒性,笔者将以上4个模型分别训练5次并保存模型权重,然后加载各模型权重,将测试集的时频谱作为模型输入测试准确度。

不同结构模型测试精度如图10所示。

图10 不同结构模型测试精度

从测试集的表现可看出:在每次独立计算中,双通道模型表现的测试精度总是比单通道高,而其他3种模型每次计算的测试精度不是很稳定。

通过以上分析可以证明,所提的算法不但具有着较强的鲁棒性,而且模型的稳定性能也优于其他3种单通道CNN方法。

5 结束语

笔者提出了一种结合多次同步压缩变换(MSST)技术及双通道卷积神经网络(TCNN)用于变转速滚动轴承故障智能诊断新方法。

主要研究结论如下:

(1)通过使用不同尺寸的小卷积核TCNN进行提取时频图谱中的故障特征信息,并进行融合后,提高了模型的特征提取能力;通过一组实验数据验证了该技术可以实现在变转速工况下的滚动轴承故障诊断;

(2)该模型通过采用小尺寸卷积核代替大卷积核,不仅减少了网络所需的参数量,而且还增强了网络的非线性拟合能力;采用小尺寸卷积核更能充分地挖掘故障特征中的细小特征,从而提高了模型的识别度。

实验结果也表明:与单通道卷积神经网络结构相比,所提的模型表现出收敛速度快、训练稳定，并且模型有较强的特征提取能力和鲁棒性,可有效应用于变转速滚动轴承故障诊断中,为变转速滚动轴承故障智能诊断提供了一种新思路。

此外,笔者下一步的研究方向是结合CNN算法,如何有效地发掘原始变转速振动信号中的故障特征信息,以实现“端到端”的诊断模式。