基于粒子群-小波神经网络的水工隧洞造价预测
李天翔,黎伞伞
(1.中国电建集团贵阳勘测设计研究院有限公司,贵阳 550081; 2.贵州理工学院,贵阳 550003)
项目前期阶段是工程建设的初始阶段,其造价文件成果是投资决策的重要参考依据,对工程的投资起着宏观控制的作用。在项目建设各阶段中,项目前期阶段对造价的影响程度最高。使用计价定额能准确计算出工程的前期造价,但是需要花费大量的时间,因此如何快速而准确地预测工程造价是众多学者关注和研究的焦点。水利水电工程往往受自然条件制约多、施工条件复杂、工期长、范围广,同时大部分工程均为非标准化设计,这些因素都给项目的造价求解增加了难度。吁莎[1]用模糊数学理论对水电工程造价案例进行筛选,再采用BP神经网络,实现水电工程特征与造价之间的复杂非线性映射;迟晓梅[2]通过分析国内水利工程造价估算中存在的问题,将粒子群算法与水利工程造价候选方案进行动态映射,将参数约束问题转换成函数,形成动态模型;王建[3]运用灰色系统理论的原理和方法,建立水利工程造价估算模型,并对估算结果进行检验。本文在粒子群算法和小波神经网络理论的基础上,构建隧洞的造价预测模型,并利用实际工程检验其有效性。
1 粒子群-小波神经网络算法
1.1 小波神经网络
小波神经网络是将小波变换和人工神经网络结合后发展起来的,小波神经网络继承了小波变换的多分辨率分析的特性,使其能够对具体奇异信号进行精确识别,具有更强的非线性映射能力。基于这种特性,小波神经网络被广泛应用于函数逼近、参数辨识、图像处理等领域。小波神经网络包含输入层、隐含层、输出层3层结构,其结构见图1。

图1 小波神经网络结构
图1中x1,x2,…xm为小波神经网络的输入值;y1,y2,…yn为小波神经网络的输出值;ψ为小波函数。
小波神经网络隐含层的输出计算公式为:
(1)
式中:ψa,b(hj)为隐含层中第j个节点的输出值;xk为小波神经网络输入值;wjk为输入层和隐含层的连接权值;bj为小波基函数的平移因子;aj为小波基函数的伸缩因子;ψ为小波函数,选用满足框架条件的Morlet小波函数,其公式为:
(2)
小波神经网络输出层的计算公式为:
(3)
式中:wij为隐含层与输出层的连接权值;ψa,b(hj)为隐含层中第j个节点的输出值。
用均方根误差来反映学习的性能,其表达式为[4]:
(4)
小波神经网络的学习和训练方式与BP网络基本相同,通过误差反传来调整权值和阈值。
1.2 粒子群算法
粒子群优化算法是一种以群智能随机优化计算为基础的算法,它模拟的是鸟群社会系统,它不要求函数具有可微、可导等特性,因而使用广泛。粒子群更新公式如下[5]:
(5)
(6)
(7)
式中:wmax、wmin分别为惯性权值的最大值和最小值;t为当前迭代次数;Tmax为最大迭代次数;c1、c2为学习因子;r1、r2为在区间[0,1]之间的随机数;xid为粒子位置;vid为粒子速度;pbest为个体最优位置;gbest为群体最优位置。
采用粒子群算法优化小波神经网络的初始权值及阈值,能够省去一部分梯度下降法中误差调整的过程,加快了小波神经网络的训练速度,避免陷入局部最优点,提高了网络的泛化能力。
2 工程应用
2.1 工程概况
某工程中的两个隧洞埋深均较大,衬砌为C25混凝土,隧洞洞身布置排水孔φ50@3×3 m,L=2 m。隧洞一总长度为1 327.3 m,过流断面为3 m×3.5 m(宽×高),III类围岩占总长度的17.9%,IV类围岩占总长度的78.2%,V类围岩占总长度的4.0%。隧洞二总长度为385.67 m,过流断面为3.5×4.0 m(宽×高),III类围岩占总长度的19.90%,IV类围岩占总长度的73.50%,V类围岩占总长度的6.60%。
2.2 造价影响因素敏感性分析
选择隧洞一作为研究对象进行造价影响因素的敏感性分析,影响隧洞每延米造价的主要因素有:
1) 围岩类别。根据相关设计规范,不同围岩类别往往采用的断面形式也不同,本工程采用的断面形式见表1。

表1 各围岩类别对应的断面形式
2) 岩石级别。岩石的级别越高, 其强度越高, 钻孔的阻力越大, 工效越低, 对爆破的抵抗力越大, 所需的炸药也越多[6]。
3) 断面面积。断面面积越小,隧洞各项目的工程量越小,但是出渣及开挖的效率降低,石方开挖的难度逐渐增大,超挖百分比也增大。
4) 隧洞长度。隧洞的长度增加,机械的运输效率降低,隧洞内通风的费用也将增加。
将隧洞一的特征值(IV类围岩、Ⅸ-Ⅹ级岩石,隧洞断面面积10.5 m2,隧洞长度1.3 km)作为敏感性分析的基准值,并求得基准值对应的每延米隧洞的投资;只改变基准值中的某一个因素,其他因素与基准值保持一致,求得各因素引起的每延米单价变化见表2。
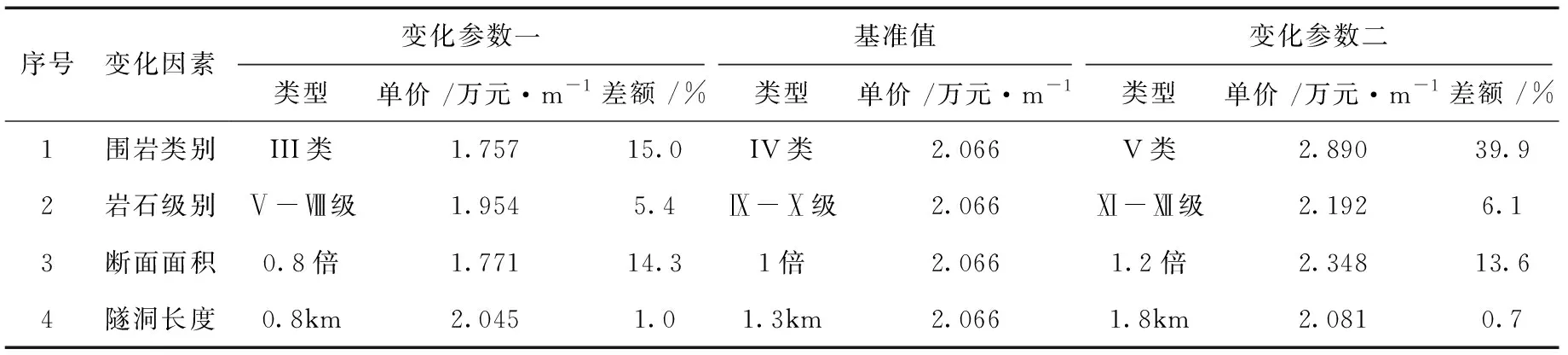
表2 各因素引起每延米单价变化
根据计算结果可知,影响隧洞每延米单价的各因素按影响程度大小依次排列为:围岩类别>断面面积>岩石级别>隧洞长度。
2.3 造价预测
根据敏感性分析成果,选取各类围岩所占百分比、平均过水断面面积、岩石级别(Ⅴ-Ⅷ取1,Ⅸ-Ⅹ级取2,Ⅺ-Ⅻ级取为3)、隧洞长度作为网络输入,对应的隧洞每延米投资作为网络输出。小波神经网络的训练样本可根据以往工程统计结果分析得到,具体见表3。
将训练样本数据按照式(8)进行归一化处理,使其在区间[-1,1]之内:
(8)
式中 :xt为归一化处理后在区间[-1,1]的数据;x为未归一化的数据。
小波神经网络隐含层节点数量根据以下经验公式计算[7]:
(9)
式中:nb为隐含层节点数;ni为输入层节点数;n0为输出层节点数;α为1~10之间的常数。
经计算,当nb=6时,网络训练的误差较小,此时小波神经网络的结构为6-6-1的形式。
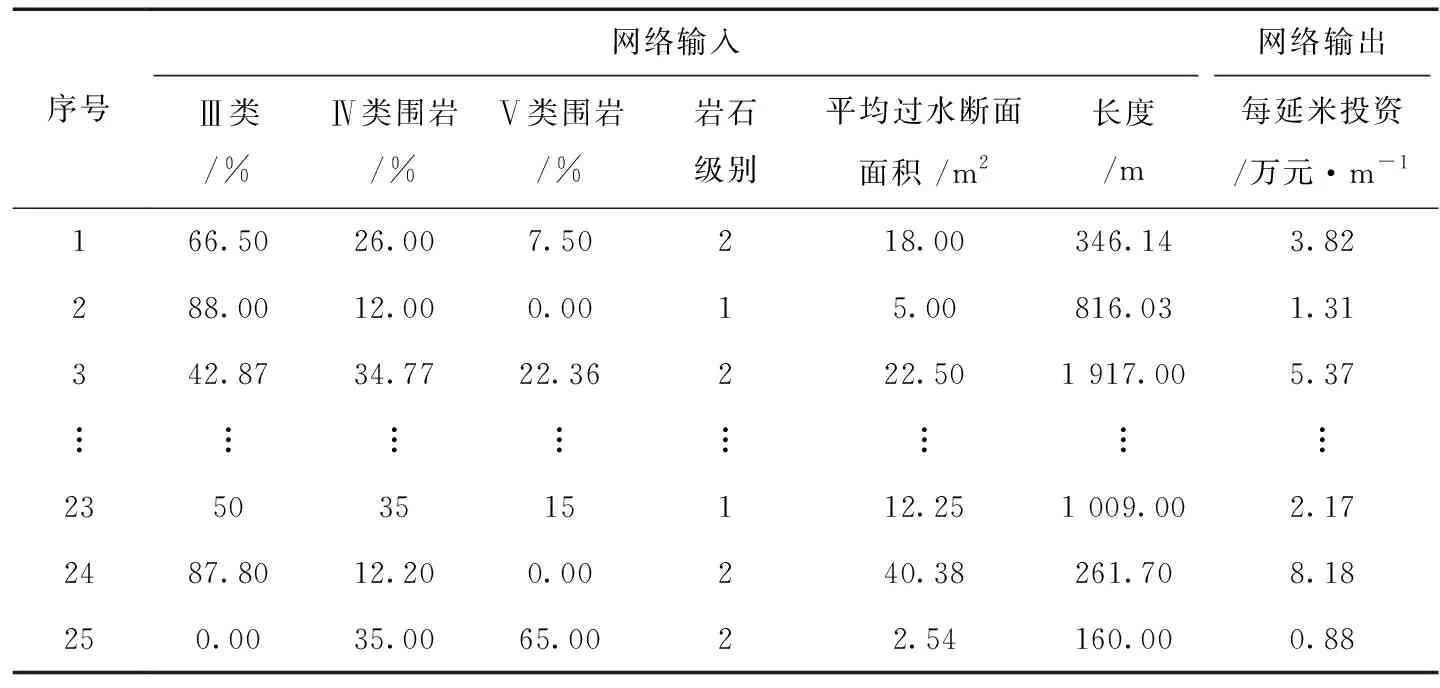
表3 小波神经网络训练样本
将训练样本输入到粒子群-小波神经网络中进行训练,经过3 675次迭代,小波神经网络的均方根误差达到0.003。若小波神经网络的初始值未经粒子群算法优化,则需要5 873次迭代,才能使均方根误差达到0.003。将测试样本数据按照式(8)归一化处理后输入到训练好的小波神经网络中,测试样本见表4。

表4 小波神经网络测试样本
将测试样本输出反归一化得到每延米隧洞的造价预测值,乘以隧洞长度即得到隧洞的造价,隧洞造价预测值及实际值见表5。

表5 隧洞造价预测值及实际值
由表5可知,使用粒子群-小波神经网络进行造价预测,计算速度较快,误差较小,精度满足项目前期投资决策的需要。
3 结 论
将粒子群-小波神经网络算法应用于造价预测中,主要得到如下结论:
1) 围岩级别、断面面积等因素对隧洞的投资起关键性作用。
2) 粒子群算法的应用减少了小波神经网络的迭代次数,提高了网络的泛化性能和预测精度。
3) 粒子群-小波神经网络应用于造价预测中,与实际值较为接近。本预测模型亦可用于其他类型水工建筑物的造价预测中。

