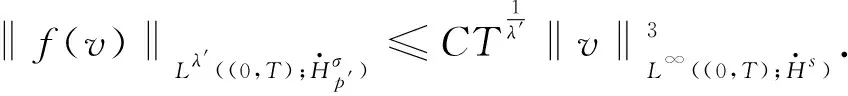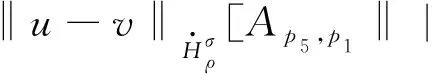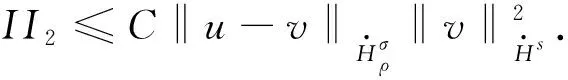Hartree型非线性薛定谔方程解的无条件唯一性
武江雪,韩 征,方聪慧,付 雪
(杭州师范大学数学学院,浙江 杭州 311121)
1 绪论
本文主要研究了Hartree型非线性薛定谔方程的解在Sobolev空间中的无条件唯一性,其方程如下:

(1)
其中n≥1,γ∈,T>0,s>0,0<β 参考文献[1-12]研究了该方程在Sobolev空间中的柯西问题.特别地,苗长兴等人[9]证明了该方程在Hs(n) 中的局部适定性问题,其中 以下是本文的主要结论: 0<β 则方程 (1) 的解在L∞((0,T);Hs) 中的无条件唯一性成立. 0<β 则方程 (1) 的解在L∞((0,T);Hs) 中的无条件唯一性成立. 3s+1≤β<2s+2. 注记1由以上结论,可对方程 (1) 解的无条件唯一性作出如下总结: 1)对于n=1 和n≥7,s>0,0<β 定义1如果q,r满足下列条件,则称(q,r)为一组相容对. 引理1(经典的Strichart估计[17]). 1)对 ∀φ∈L2(n),函数U(t)φ属于Lq(,Lr(n))∩C(,L2(n)),其中(q,r)为相容对.则存在一个常数C,使得对∀φ∈L2(n),有 ‖U(·)φ‖Lq(;Lr)≤C‖φ‖L2. 2)已知区间I⊂,令若(γ,ρ)是一组相容对,且f∈Lγ′(I;Lρ′(n)),则对任意的相容对(q,r),我们有 其中t∈I.而且,存在一个与I无关的常数C,对∀f∈Lγ′(I;Lρ′),使得下面的式子成立 ‖Φf(t)‖Lq(I;Lr)≤C‖f‖Lγ′(I;Lρ′). (2) 引理2(非齐次Strichartz估计[18]) 对∀σ∈,满足下列条件: 已知区间I⊂,令如果(q,r) 是一组相容对且则对任意的一个相容对 (γ,ρ),存在一个与I无关的常数C,使得 其中γ,ρ,q和r满足如下条件 (3) 且还需满足以下条件之一: 如果n=2,则r,ρ<∞; 如果n≥3,则需分以下两种情况: (4) 引理3(Hardy-Littlewood-Sobolve不等式[19]).若 0<β 其中 1 ‖|x|-β*f‖Lq≤Ap,q‖f‖Lp. 则存在一个常数C,使得 (5) 证明根据对偶的性质来证明方程(5),即转化为证明下面的不等式: 由Hölder不等式可得 又由三角不等式和Hölder不等式可得 综上所述,可得 故引理得证. 引理7令 0<β (6) 则存在一个常数C,使得 ‖[|x|-β*(fω)]h‖Lp≤C‖f‖Lr‖ω‖Hs‖h‖Hs. ‖[|x|-β*(fω)]h‖Lp≤C‖|x|-β*(fω)‖Lp1‖h‖Lp2≤C‖fω‖Lp3‖h‖Lp2, C‖fω‖Lp3‖h‖Lp2≤C‖f‖Lr‖ω‖Lp2‖h‖Lp2≤C‖f‖Lr‖ω‖Hs‖h‖Hs. 由引理1可得 ‖u-v‖Lq((0,T);Lr)≤‖f(u)-f(v)‖La′((0,T);Lb′), (7) 其中(a,b) 是另一组相容对. (8) (9) 对于II,由三角不等式得 (10) (II1)≤‖u-v‖Lr‖u‖Hs‖v‖Hs. (11) 同理可得 (12) 因此,由方程(7)—(12)和关于t运用Hölder不等式,其中若q,r,a,b,p1和p2满足 (13) 则有 (14) 所以,当β和s满足条件 即可保证条件(13)成立. 因此,如果T充分小,则方程(14)右端可被左端吸收,从而无条件唯一性得证. 由引理2可知 ‖u-v‖Lq((0,T);Lr)≤‖f(u)-f(v)‖La′((0,T);Lb′), 类似于上面的证明,我们有 ‖f(u)-f(v)‖Lb′≤C‖u-v‖Lr(‖u‖Hs+‖v‖Hs)2. 综上所述,定理1和定理2证明完毕. (15) 由引理2可得 (16) (17) 同理可得 (18) 由方程(15)—(17)及关于t运用Hölder不等式,我们可得 (19) 又由三角不等式可得 又由方程(21)可得 (22) 而对于II,可转化为 (23) 由引理6可得 (24) 同理可得 (25) 因此,由方程(19)—(22)和关于t运用Hölder不等式可得 (26) 其中(γ,ρ),(λ,p),(q,r)满足条件(2),(3),(4),即 (27) (28) 所以,当T充分小时,方程(26)的右端可以被左端吸收,则无条件唯一性成立. 由以上关系可得,当2≤n≤6时,要使条件(26)和(27)成立,β和s需满足以下条件: 当n≥7时,要使条件(27)和(28)存在,β和s需满足先前假设(15).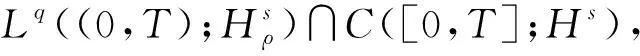
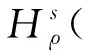


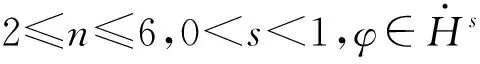



2 准备工作




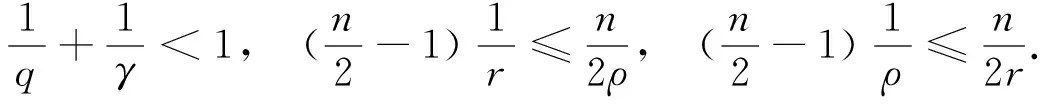











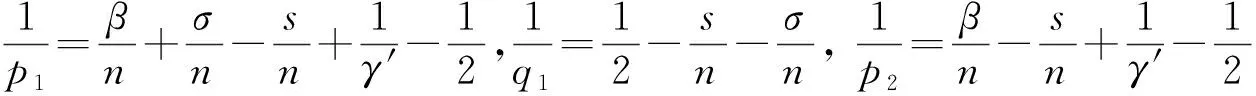





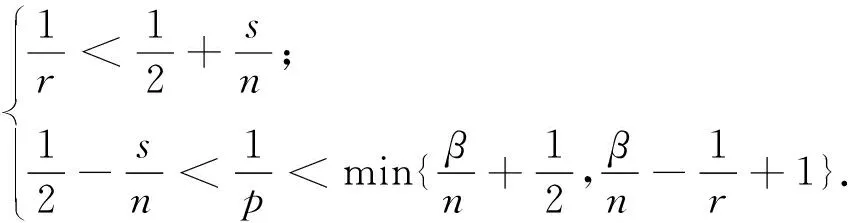
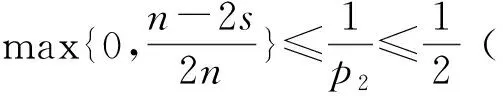

3 定理1和 定理2的证明
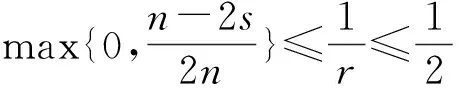
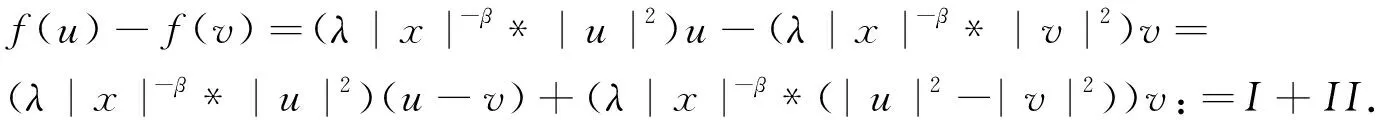

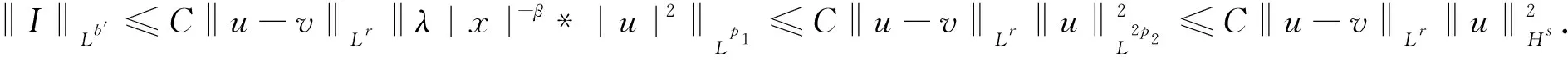

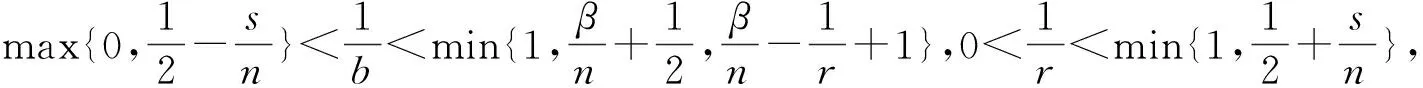
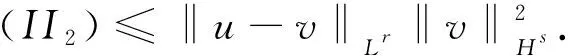

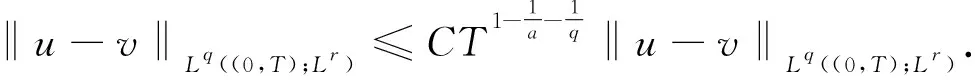
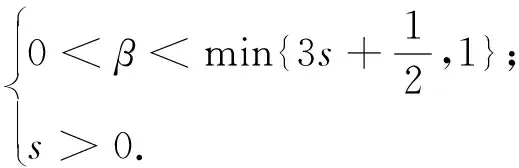
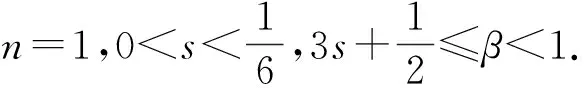



4 定理3和定理4的证明