Three-factor Multi-server Authentication Scheme for Multimedia Social Networks without Registration Center
XIE Qi, MU Hang
(Key Laboratory of Cryptography of Zhejiang Province, School of Mathematics, Hangzhou Normal University, Hangzhou 311121, China)
Abstract: Since more and more people use multimedia social networks (MSN) to share multimedia information (MI) or obtain MI from MSN, therefore, multi-server authentication plays an important role in MSN, which can prevent users from registering to each server and remembering each password in single server authentication mechanism. Recently, Chaudhry points out that two three-factor multi-server authentication schemes for MSN proposed by Lu et al. suffer from impersonation attack and do not provide user anonymity. To fix these problems, Chaudhry proposes a security enhancement scheme, and claims that his scheme is secure. However, his scheme lacks of perfect forward secrecy and session key secrecy, and suffers from insider impersonation attack and man-in-the-middle attack. Therefore, this paper proposes a new three-factor multi-server authentication scheme without registration center (RC). It further proves the security of the proposed scheme by using formal verification tool ProVerif which bases on applied pi calculus, and demonstrates that it has high computational efficiency by comparison with some related schemes.
Key words: multimedia social networks; multi-server; authentication; bioinformation; ProVerif
1 Introduction
Multimedia social networks (MSN), such as YouTube, LinkedIn and Facebook, are widely used nowadays. Many people publish their multimedia information (MI), such as papers, pictures, videos and music, in MSN, and browse MI in MSN. In single server authentication mechanism, user needs to register him on to different servers and remember different passwords. Once he wants to access different MSN, he should use different passwords to login to different servers. However, it is inconvenience. Multi-server authentication allows user register onto registration center (RC) once, just remember one password and can pass through the authentication of all servers and obtain the services from all servers.
By scrutinizing the proposed multi-server authentication schemes, they can be divided into two categories according to whether RC participates in the authentication process. If the authentication process needs RC participation, it may need more communication and computation costs, RC will also be bottleneck once many users want to login to servers at the same time. Obviously, the schemes without RC participation may cost-efficient. In terms of lightweight design, multi-server authentication schemes can be categorized into password based[1-2], two-factor (password and smart card) based[3-14], and three-factor (password, smart card and biometrics) based[15-20]schemes. In this paper, we focus on three-factor based multi-server authentication scheme without RC participation.
1.1 Related works
In 2013, Yoon et al.[21]proposed elliptic curve cryptography (ECC) based three-factor multi-server authentication scheme. Later on, Shen et al.[22]showed that their scheme is vulnerable to impersonation attack, insider attack, and password guessing attack, and then they proposed an improved scheme. But Li et al.[23]showed that Shen et al.’s scheme suffers from denial-of-service attack and lacks of user anonymity, and then they proposed an improved scheme. In 2018, Irshad et al.[24]pointed out that Tan’s scheme[12]suffers from impersonation attack and password guessing attack, and proposed a new one. However, the above schemes need RC participate in the authentication process, it may need more communication and computation costs.
In order to improve efficiency, in 2014, Chuang et al.’s[25]proposed three-factor multi-server authentication scheme without RC participating the authentication process. Unfortunately, Lin et al.[26]pointed out that their scheme cannot resist server spoong attack and impersonation attack, lacks of user anonymity and session key secrecy. Then, they proposed an improvement of Chuang et al.’s protocol. In 2016, Irshad et al.[27]pointed out that Jiang et al’s scheme[28]suffers from traceability and stolen-verier attack, and proposed a chaotic map based multi-server authentication scheme without engaging RC. The same year, Chaudhry[29]pointed out that Lu et al.’s schemes[30-31]suffer from impersonation attacks and lack of user anonymity, an then he proposed a new three-factor multi-server authentication scheme. In 2018, Irshad et al.[32]proposed a new multi-server authentication scheme for critical systems.
1.2 Our contribution
In this paper, we showed that Chaudhry’s scheme[29]is insecure, which suffers from insider impersonation attacks and man-in-the-middle attacks, lacks of session key secrecy and perfect forward secrecy, and then propose a new three-factor multi-server authentication scheme. The proposed scheme can resist various known attacks, and has some advantages, such as user anonymity, no RC participation, and perfect forward secrecy. We use formal verification tool ProVerif to prove the authentication and secrecy of our scheme.
2 Review of Chaudhry’s Scheme
We will introduce Chaudhry’s three-factor multi-server authentication scheme, which including initialization, server registration, use registration, authentication and key agreement, and password change. In this section, we only introduce the first four phases. The notations are as follows.
·IDu: the userUi’s identity.
·SIDj: the serverSj’s identity.
·PWu:Ui’s password.
·Ep(a,b): elliptic curve selected by registration center (RC).
·ru: a random number.
·nu: a random number selected byUi.
·ns: a random number selected bySj.
·Biu: personal biometrics ofUi.
·SKRS: secret key shared between RC and allSj.
·PKSj,SKSj: public key and secret key ofSj.
·h(·): a secure collision-free one-way hash function.
·H(·): a biological hash function.
· ⊕: the bitwise XOR operation.
· ‖: the concatenation operation.
·SCu: smart card ofUi.
·Ek(),Dk(): secure symmetric encryption and decryption functions with the keyk.
2.1 Initialization
The registration center RC selects an elliptic curveEp(a,b) and a base pointP, the one-way hash functionh(·) and the biological hash functionH(·), and then selects a secret keySKRSshared with all servers. Finally,RCpublishesEp(a,b),h(·) andH(·).
2.2 Server registration
In this phase, all serversSjregister onto the RC as follows.
Sjselects his identitySIDjand his private keySKSj, calculates his public keyPKSj=SKSj·P, and then sendsSIDjandPKSjto the RC. After receiving the registration information, RC sends it’s secret keySKRStoSjvia a secure channel, and publishes the public keyPKSj.
2.3 User registration
In this phase, all usersUiregister onto the RC as follows.
Step1:Uiselects his identityIDuand passwordPWu, and enters the biometric informationBiu, and sends {IDu,h(PWu‖H(Biu))} to RC through a secure channel.
Step2: After receiving the registration information, RC calculatesVu=h(IDu‖h(PWu‖H(Biu))) andh(SKRS‖IDu). Then, RC storesVuandh(SKRS‖IDu) into the smart card (SCu) and issues it toUithrough a secure channel.
Step3: After obtainsSCu,Uicalculates
Yu=h(SKRS‖IDu)⊕h(PWu‖IDu‖H(Biu)),
and replacesh(SKRS‖IDu) withYuinSCu. That is,SCucontains{Vu,Yu,h(),H()}.
2.4 Authentication and key agreement
In this phase,UiandSjcomplete mutual authentication and generate a secure session key.
Step1:UiinputsIDu,PWuandBiu, and insertsSCuinto the card reader,SCucalculates
Vu′=h(IDu‖h(PWu‖H(Biu)))
and compares whetherVu=?Vu′ or not. If not, rejects it. Otherwise,SCugenerates two random numbersruandnu, calculates
Ku=ru·PKSj,M1=ru·P,M2=IDu⊕Ku,
h(SKRS‖IDu)=Yu⊕h(PWu‖IDu‖H(Biu))
M3=nu⊕h(h(SKRS‖IDu)‖SIDj),
Zu=h(h(SKRS‖IDu)‖nu‖Ku‖T1),
whereT1is a current timestamp. ThenUisends {Zu,M1,M2,M3,T1} toSj.
Step2: After received the message fromUi,Sjchecks the freshness of the timestampT1.Then computes
Ku′=SKSj·M1,IDu′=M2⊕Ku′,
nu′=M3⊕h(h(SKRS‖IDu′)‖SIDj),Zu′=h(h(SKRS‖IDu′)‖nu‖Ku‖T1).
and verifies ifZu=Zu′. If not, rejects it. Otherwise,Sjgenerates a random numbernsand calculates
M4=ns⊕Ku,
M5=h(IDu‖nu′‖ns‖Ku‖T2),
SKji=h(IDu‖nu′‖ns‖Ku),
whereT2is a current timestamp andSKjiis a session key. ThenSjsends the message {M4,M5,T2} toUi.
Step3: After receiving {M4,M5,T2},Uichecks the freshness of the time stampT2, calculates
ns′=M4⊕Ku,M5′=h(IDu‖nu‖ns′‖Ku‖T2)
and then compares ifM5=M5′ is correct. If not, rejects it. Otherwise,Uicomputes
SKij=h(IDu‖nu‖ns′‖Ku),M6=h(SKij‖IDu‖ns′‖T3),
whereT3is a current timestamp. ThenUisends {M6,T3} toSj.
Step4: After receiving {M6,T3},Sjverifies the freshness of the time stampT3and verifies whetherM6=h(SKji‖IDu‖ns‖T3) is correct. If not, terminates it. Otherwise, mutual authentication is completed and the session key is established.
3 Weaknesses of Chaudhry’s Scheme
Though Chaudhry claimed that his scheme can resist various known attacks, we found that his protocol has some weaknesses.
3.1 No session key secrecy
In Chaudhry’s scheme, if an adversary is a legitimate serverSm, and the userUihas ever been logged in it, soSmhas known the identityIDuofUi, and can computeh(SKRS‖IDu)by using the secret keySKRSshared withRC. WhenUiand another legitimate serverSjauthenticate each other and establish a session keySKij=h(IDu‖nu‖ns‖Ku), the adversarySmcan obtain {Zu,M1,M2,M3,T1} and {M4,M5,T2} by public channels, and the identitySIDjofSjis easily available. Therefore,Smcan computeKu=M2⊕IDu,nu=M3⊕h(h(SKRS‖IDu)‖SIDj),ns=M4⊕Ku. Thus, the adversarySmcan compute the session keySKij=h(IDu‖nu‖ns‖Ku) shared betweenUiandSj.
3.2 No perfect forward secrecy
Because the session key isSKij=h(IDu‖nu‖ns‖Ku) in Chaudhry’s scheme, whereIDuis the identity ofUi,nuandnsare random nonce chosen byUiandSjrespectively,Ku=ru·PKSj=M1·SKSj, whereSKSjis the secret key ofSj,SKRSis a secret key shared betweenRCand allSj,nu=M3⊕h(h(SKRS‖IDu)‖SIDj),ns=M4⊕Ku. Therefore, if the private keySKSjofSj, secret keySKRSshared between RC and allSj, and the identiesIDuandSIDjare compromised, then the session keySKijcan be computed.
3.3 Insider impersonation attack
If an adversary is a legitimate serverSm, who can impersonate another legitimate serverSj, once the userUihas ever been logged inSmand want to loginSj, becauseSmhas known the identityIDuof theUi, and can computeh(SKRS‖IDu) by using the secret keySKRSshared with RC. WhenUilogs onto serverSjand sends {Zu,M1,M2,M3,T1} toSj,Smintercepts and calculatesKu=M2⊕IDu, generates a random numbernsand calculatesM4=ns⊕Ku,nu=M3⊕h(h(SKRS‖IDu)‖SIDj),M5=h(IDu‖nu‖ns‖Ku‖T2),SKji=h(IDu‖nu′‖ns‖Ku), returns {M4,M5,T2} toUi. Obviously,Uican computensand verify the correction ofM5, and can generate the session keySKji, which shared with the adversarySmnot theSj.
On the other hand, if an adversary is a legitimate serverSm, who can impersonate userUionce the userUihas ever been logged inSm. WhenUiwants to log onto another legitimate serverSjand sends {Zu,M1,M2,M3,T1} toSj,Smintercepts and calculatesM1=ru′·P,M2′=IDu⊕ru′·PKSj,M3′=nu′⊕h(h(SKRS‖IDu)‖SIDj) andZu′=h(h(SKRS‖IDu)‖nu′‖ru′·PKSj|T1′), whereru′ andnu′ are random chosen bySm. ThenSmsends {Zu′,M1′,M2′,M3′,T1′} toSj. Obviously,Smcan be authenticated bySj, andSjcan generate and share a session key withSmnotUi.
3.4 Suffer from man-in-the-middle attack
According to above analysis, a legitimate serverSmcan impersonate another legitimate serverSjto cheat a userUi, andSmcan also impersonateUito cheat another legitimate serverSj, so Chaudhry’s scheme can not resist the man-in-the-middle attack.
3.5 An error
In authentication and key agreement of Chaudhry’s scheme,UicomputesM2=IDu⊕Kuandns′=M4⊕Ku, andSjcomputesIDu′=M2⊕Ku′ andM4=ns⊕Ku, may unworkable. The reason is thatKuis a point of elliptic curve,IDMUandnsare integer numbers. To fix these problems, we can correct them asM2=IDu⊕h(Ku) andM4=ns⊕h(Ku).
4 The proposed scheme
Our proposed scheme also contains initialization, server registration, use registration, authentication and key agreement, and password change. The initialization is the same as that of Chaudhry’s scheme, the other phases are as follows.
4.1 Server Registration
Sjselects his identitySIDjand sends it to registration center RC, RC selects his private keyxand computess=h(SIDj‖x),PKSj=sP, and then sendsstoSjvia a secure channel, publishesSIDjandPKSj,Sjkeepssin secret.
4.2 User Registration
UserUiselects a random numbern, his identityIDuand passwordPWu.Then inputs his biometric informationBiu, computesRPWu=h(IDu‖PWu‖n), and sends {RPWu,IDu} to RC via a secure channel.
RC computesu=h(IDu‖x),PKu=u·P,Xi=u⊕RPWu, and storesPKuandXiin a smart cardSCu, and then sendsSCutoUivia a secure channel. Finally, RC publishesIDuandPKu.
UicomputesXu=Xi⊕RPWu⊕h(IDu‖PWu‖H(Biu))=u⊕h(IDu‖PWu‖H(Biu)),V=h(u). At last,SCucontainsPKu,VandXu.

4.3 Authentication and Key Agreement
In this phase,UiandSjcomplete mutual authentication and generate a secure session key. The process is illustrated in Fig.1
Step1:Uiinserts his smart cardSCuinto a card reader, and inputs hisBiu,IDuandPWu,SCucomputesu=Xu⊕h(IDu‖PWu‖H(Biu)),and verifies whetherV=h(u) or not. If it is not correct, re-does it again. Otherwise,SCugenerates a random numbera, computes
V1=uPKSj=h(IDu‖x)h(SIDj‖x)P,
V2=aP,
V3=aPKSj=asP=ah(SIDj‖x)P,
V4=h(V3‖t1)⊕IDu,
V5=Eh(V3)(V1‖IDu‖SIDj‖V2‖V3‖V4‖t1),
wheret1is current timestamp. ThenSCusendsm1={SIDj,V2,V4,V5,t1} toSj.
Step2: After receivingm1={SIDj,V2,V4,V5,t1},Sjfirst checks the freshness of the timestampt1, then computesV3=sV2=h(SIDj‖x)V2=ah(SIDj‖x)P,IDu=h(V3‖t1)⊕V4. According toIDuobtainsPKu, and computesV1′=sPKu=h(IDu‖x)h(SIDj‖x)P,Dh(V3)(V5)={V1‖IDu‖SIDj‖V2‖V3‖V4‖t1}, and checks the correction of {V1′,IDu,SIDj,V2,V3,V4,t1}. If no, rejects it. Otherwise,Sjselects a random numberb, computes
V6=bP,
SKji=h(bV2‖V1‖V6‖IDu‖SIDj‖V2‖t1‖t2)
V7=Eh(V3)(V6‖IDu‖SIDj‖SKji‖V2‖t2),
wheret2is current timestamp. ThenSjsendsm2={V7,t2} toSCu.
Step3:SCuchecks the freshness of the timestampt2, and computesDh(V3)(V7)={V6‖IDu‖SIDj‖SKji‖V2‖t2}, checks the correction of {IDu,SID,V2,t2}, then computesSKij=h(aV6‖V1‖V6‖IDu‖SIDj‖V2‖t1‖t2), and checks ifSKji=SKij. If not, reject it. Otherwise, the mutual authentication is completed, and the session keySKjiis established.
4.4 Password Change
IfUiwants to change his password, he can insert hisSCuinto a card device, enter his old passwordPWuand new passwordPWu′, along with hisBiuandIDu.
SCucomputesXu⊕h(IDu‖PWu‖H(Biu))=u′, and checks ifV=h(u′). If not, re-entersPWutillV=h(u′). Otherwise,SCucomputesXu′=u′⊕h(IDu‖PWu′‖H(Biu)). At last,SCucontainsPKu,VandXu′.
5 Security analysis
In this section, we show that the proposed scheme is secure.
5.1 Password guessing attack
If an adversary can know all information {PKu,V,Xu} stored in smart cardSCu, and wants to guessPWuand computeu=Xu⊕h(IDu‖PWu‖H(Biu)). Unfortunately, he cannot knowBiuand cannot compute and verify the correction ofu, becauseBiuis not easy to be imitated and guessed. Therefore, the adversary cannot verify whether the guessed password is correct or not.
5.2 Impersonation attack
If an adversary wants to impersonateUi, he generatesaandV1, computesV2=aP,V3=aPKSj=asP=ah(SIDj‖x)P,V4=h(V3‖t1)⊕IDuandV5=Eh(V3)(V1‖IDu‖SIDj‖V2‖V3‖V4‖t1), and sendsm1={SIDj,V2,V4,V5,t1} toSj. However,V1generated by the adversary cannot pass through the authentication, becauseV1=uPKSj=h(IDu‖x)h(SIDj‖x)P=h(SIDj‖x)PKu=sPKu, and the adversary does not knowuands, so he cannot computeV1fromPKuandPKSjdue to the Elliptic Curve Diffie-Hellman problem (ECDHP).
If an adversary wants to impersonateSj, because he does not knows, so he cannot computeV3=sV2=asP=ah(SIDj‖x)Pwhen the adversary receivesm1={SIDj,V2,V4,V5,t1} fromUi, he can also not obtainV1fromV5. Therefore,SKjiandV7generated by the adversary cannot pass through the authentication ofUiwithout knowingV1.
5.3 Man-in-the-middle attack
Due to the above analysis, we can know that an adversary neither can impersonate the user nor can impersonate the server, so our scheme can resist the man-in-the-middle attack.
5.4 Perfect forward secrecy
Even if an adversary can know {Biu,PWu,IDu} of the userUiand secret keysof the serverSj, he still cannot compute the session keySKji=h(bV2‖V1‖V6‖IDu‖SIDj‖V2‖t1‖t2), because he cannot computebV2=abPfromV6=bPandV2=aP, which may suffer from ECDHP.
5.5 Replay attack
The random nonce {a,b} and the timestamps {t1,t2} are used in our scheme, which can resist replay attack.
5.6 Known session key security
In our scheme, random nonce {a,b} are different in each session, so an adversary cannot compute the before and the future session key even if he can know one session key.
5.7 Anonymity and unlinkability
The identityIDuofUiis contained in {V4,V5,V7}, which is different in each session and is protected by hash function and encryption function, and an adversary cannot computeV3andV1. Therefore, our scheme keeps anonymity and unlinkability.
6 Formal verification
We apply applied pi calculus[33]based formal verification tool ProVerif[34]to verify authentication and security of our protocol, which is an automated verification tool that can handle symmetric and asymmetric cryptography, hash functions and digital signatures, and evaluate the security attributes of the authentication protocol. The ProVerif code can be divided into three prats.
First part is the definitions of message transmission channels, constants, variables and functions etc. There are three kinds of channels:rsschandruschare defined as private channels in server and user registration phases,cchis defined as a public channel in authentication and key agreement phase.
freerssch:channel[private].
freerusch:channel[private].
freecch:channel.
All variables and constants are defined as:SIDjandIDuare the identities of server and user,pis a base point,PWuandBiare user’s password and biometric information,xis the private key of RC,SKijandSKjiare session keys shared between a user and a server.
freeSIDj:bitstring[private].
constx:bitstring.
constp:bitstring.
freeSKij:bitstring[private].
freeSKji:bitstring[private].
freeIDu:bitstring[private].
freePWu:bitstring[private].
freeBi:bitstring[private].
The functionsh/H,concatare the secure one-way hash functions and the bit concatenate function,xorandmultare xor operation and the multiplication on ECC, respectively. All functions are defined as follow:
funh(bitstring):bitstring.
funh(bitstring):bitstring.
funH(bitstring):bitstring.
funxor(bitstring,bitstring):bitstring.
funinverse(bitstring):bitstring.
funmult(bitstring,bitstring):bitstring.
funconcat(bitstring):bitstring.
funsenc(bitstring,bitstring):bitstring.
equationforalla:bitstring,b:bitstring;xor(xor(a,b),b)=a.
equationforalla:bitstring,b:bitstring;mult(b,mult(a,p))=mult(a,mult(b,p)).
reducforallkey:bitstring,m:bitstring;sdec(senc(m,key),key)=m.
tableregtable(bitstring,bool).
The events are defined as:
eventUsignS(bitstring).
eventSauthU(bitstring).
eventSsignU(bitstring).
eventUauthS(bitstring).
The second part is the process that describes the actions of user, server and RC according to our scheme. The actions of RC are all executed in the user and server registration phase. In this phase, RC receives registration message from server and sends a secret value to server via a private channelrssch. Then he waits registration message from user and responses message to user via a private channelrusch.RegCenteris defined as:
letRegCenter=
in(rssch,xSIDj:bitstring);
newb1:bool;
getregtable(=xSIDj,b1)in
ifb1 <>truethen
insertregtable(xSIDj,true);
lets=h((xSIDj,x))in
letPKsj=mult(s,p)in
out(rssch,(s,PKsj));
out(cch,(xSIDj,PKsj));
in(rusch,(xIDu:bitstring,xRPWu:bitstring));
newb2:bool;
getregtable(=xIDu,b2)in
ifb2 <>truethen
insertregtable(xIDu,true);
letu=h((xIDu,x))in
letPKu=mult(u,p)in
letXi=xor(u,xRPWu)in
out(rusch,(Xi,PKu,xSIDj,PKsj));
out(rssch,(xIDu,PKu));
0.
The actions of server are divided into two parts. In the registration phase, server submits registration message to RC and receives response message from RC via a secure channelrssch. In the login and authentication phase, server gets request message from user, verifies user’s validity and transmits the returned message to user on a public channelcch. After that, server computes and stores it session key. The code is:
letServerj=
out(rssch,SIDj);
in(rssch,(xs:bitstring,xPKsj:bitstring));
in(rssch,(xxIDu:bitstring,xPKu:bitstring));
in(cch,(xxxSIDj:bitstring,xV2:bitstring,xV4:bitstring,xV5:bitstring,xt1:bitstring));
letV3′=mult(xs,xV2)in
letIDu′=xor(xV4,h((V3′,xt1)))in
letV1′=mult(xs,xPKu)in
let(V1″:bitstring,IDu″:bitstring,SIDj″:bitstring,V2″:bitstring,V3″:bitstring,V4″:bitstring,t1′:bitstring)=sdec(xV5,V3′)in
ifV1″=V1′then
ifIDu″=xxIDuthen
ifSIDj″=SIDjthen
ifV2″=xV2then
ifV3″=V3′then
ifV4″=xV5then
eventSauthU(V1′);
newb:bitstring;
letV6=mult(b,p)in
newt2:bitstring;
letSKji=h((mult(b,xV2),V1′,V6,xxIDu,SIDj,xV2,xt1,t2))in
letV7=senc((V6,xxIDu,SIDj,SKji,xV2,t2),V3′)in
out(cch,(V7,t2));
eventSsignU(V1′);
0.
The actions of user are also divided into two parts. In the registration phase, user submits registration message to RC and waits for message from RC through a secure channelrusch. In the login and authentication phase, user sends login message to server and receives the returned message from server on a public channelcch. After that, user checks the validity of server and computes their session key.The code is:
letUser=
newn:bitstring;
letRPWu=h((IDu,PWu,n))in
out(rusch,(IDu,RPWu));
in(rusch,(xXi:bitstring,xPKu:bitstring,xxSIDj:bitstring,xxPKsj:bitstring));
letXu=xor(xor(xXi,RPWu),h((IDu,PWu,H(Bi))))in
letV=h((xor(xXi,RPWu)))in
letu′=xor(Xu,h((IDu,PWu,H((Bi)))))in
letV′=h((u′))in
ifV′=Vthen
letV1=mult(u′,xxPKsj)in
newa:bitstring;
letV2=mult(a,p)in
letV3=mult(a,xxPKsj)in
newt1:bitstring;
letV4=xor(IDu,h((V3,t1)))in
letV5=senc((V1,IDu,xxSIDj,V2,V3,V4,t1),V3)in
out(cch,(xxSIDj,V2,V4,V5,t1));
eventUsignS(V1);
in(cch,(xV7:bitstring,xt2:bitstring));
let(V6′:bitstring,IDu′:bitstring,SIDj′:bitstring,SKji′:bitstring,V2′:bitstring,t2′:bitstring)=sdec(xV7,V3)in
letaV6′=mult(a,V6′)in
letSKij=h((aV6′,V1,V6′,IDu,SIDj,V2,t1,xt2))in
ifSKij=SKji′then
eventUauthS(SKji′);
0.
Replication(!) symbol means multiple users, servers and RCs can run at the same time, we defined a process of the scheme as the parallel executions of three parties :
process!RegCenter|!User|!Serverj
The session key secrecy and mutual authentication are verified by checking attacker queries:
queryattacker(SKij).
queryattacker(SKji).
queryid:bitstring;inj-event(SauthU(id))==>inj-event(UsignS(id)).
queryid:bitstring;inj-event(UauthS(id))==>inj-event(SsignU(id)).
We run the above process codes in ProVerif 1.95. Fig.2 displays the results that attacker query are not true. They confirm that the session key is enough secure, any attacker isn’t able to obtain or calculate session key directly.
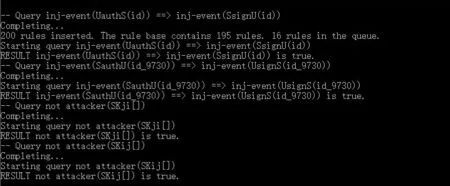
Fig.2 The results of attacker’s queries
7 Security and Performance comparison
Since the latest four schemes[29-32]without registration center are all based ECC and have well computational efficiency and security. Therefore, we only give the comparisons between our scheme and these four schemes[29-32]in terms of security and efficiency, which are given in Tab.1 and 2. LetTH,TSEandTMbe hash, symmetric encryption or decryption, and point multiplication operations, according to[35], we know that it needs 0.0023ms for a hash,0.0046ms for a symmetric encryption or decryption, and 2.226ms for a point multiplication operation in ECC.
Since all servers know the sameh(s) in[32], all servers can decrypt the message sent from any user and can know the identity of the user, so the scheme of[32]cannot provide user anonymity. From Tab.1, we can conclude that our scheme is more secure than others. Because three schemes in [29-31] do not provide perfect forward secrecy, so these schemes are efficient than other schemes according to Tab.2, but our scheme is more efficient than the scheme of [32] with perfect forward secrecy.

Tab.1 Security comparison

Tab.2 Efficiency comparison
8 Conclusion
There are many advantages in designing multi-server authentication scheme using three-factor, for example, password is easy to be remembered, smart cards can store authentication information and calculate conveniently, and biological information is not easy to be imitated and guessed. Therefore, many three-factor multi-server authentication schemes are proposed. In this paper, we scrutinize Chaudhry’s anonymous authentication scheme without RC, and show that his scheme suffers from insider impersonation attacks and man-in-the-middle attacks, lacks of session key secrecy and perfect forward secrecy, and exists an error that it may unworkable. We propose a new three-factor multi-server authentication scheme without RC, which is secure and efficient, and can be used in multimedia social networks.

