借助一元二次方程 感受数学模型魅力

文／吕 雯

纵观“一元一次方程”“二元一次方程”“分式方程”“一元二次方程”等内容，我们要学会的其实是一种数学方法——数学建模。一元二次方程是初中数学学习的重点，也是学好二次函数不可或缺的条件，更是学好高中数学的基础，还能解决生活中经常遇到的问题。从每年的中考数学试卷中，我们都能看到一元二次方程实际应用的身影。下面，就让我们一起来归纳探讨。

一、增长率问题

例1（2021·江苏盐城）劳动教育已纳入人才培养全过程，某学校加大投入，建设校园农场，该农场一种作物的产量两年内从300千克增加到363千克。设平均每年增产的百分率为x，则可列方程为________。

【解析】可先表示出第一年的产量，那么第二年的产量×（1+增长率）=363。把相应数值代入即可求解第一年的产量为300×（1+x），第二年的产量在第一年产量的基础上增加x，为300×（1+x）×（1+x），则列出的方程是300（1+x）2=363。

【点评】本题考查平均变化率问题，解题的关键在于理解平均变化率。若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b。

二、销售问题

例2（2021·山东烟台）直播购物逐渐走进了人们的生活。某电商在抖音上对一款成本价为40 元的小商品进行直播销售，如果按每件60 元销售，每天可卖出20 件。通过市场调查发现，每件小商品售价每降低5 元，日销售量增加10件。

（1）若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？

（2）小明的线下实体商店也销售同款小商品，标价为每件62.5 元。为提高市场竞争力，促进线下销售，小明决定对该商品实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？

【解析】（1）根据日利润=每件利润×日销售量，可求出售价为60 元时的原利润。设每件售价应定为x元，则每件的利润为（x-40）元，日销售量为20+=（140-2x）件。根据日利润=每件利润×日销售量，得（x-40）（140-2x）=（60-40）×20，即可得出关于x的一元二次方程x2-110x+3000=0，解得x1=50，x2=60，取较小值即可。

（2）设该商品需要打a折销售。由题意得，解得a≤8，即该商品至少需打8折销售。

【点评】这是一个生活中常见的销售类问题，解题的关键在于从实际问题中建立数学模型。通过方程模型的建立，我们能更好地感受到数学来源于生活又服务于生活，同时增强数学的应用意识。

三、面积问题

例3（2020·贵州遵义）如图，把一块长为40cm，宽为30cm 的矩形硬纸板的四角剪去四个相同小正方形，然后把纸板的四边沿虚线折起，并用胶带粘好，即可做成一个无盖纸盒。若该无盖纸盒的底面积为600cm2，设剪去小正方形的边长为xcm，则可列方程为（ ）。

A.（30-2x）（40-x）=600

B.（30-x）（40-x）=600

C.（30-x）（40-2x）=600

D.（30-2x）（40-2x）=600

【解析】设剪去小正方形的边长是xcm，则纸盒底面的长为（40-2x）cm，宽为（30-2x）cm，根据长方形的面积公式，结合纸盒的底面积是600cm2，即可得出关于x的一元二次方程（30-2x）（40-2x）=600。

【点评】本题考查用含有x的代数式表示长、宽这些量，感受用字母表示量的思想，找准等量关系，正确列出一元二次方程。

四、球赛问题

例4（2020·广西桂林）参加足球联赛的每两支球队之间都要进行两场比赛，共要比赛110 场，设参加比赛的球队有x支，根据题意，下面列出的方程正确的是（ ）。

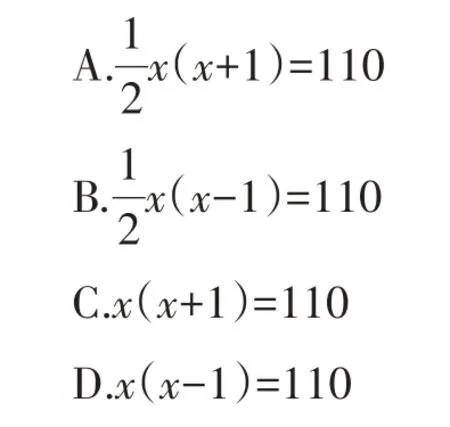
【解析】设有x个队参赛，每两队之间都进行两场比赛，共要比赛110 场，可列出方程x（x-1）=110。

【点评】本题考查由实际问题抽象出一元二次方程，我们可以根据总比赛场数作为等量关系列方程求解。

数学来源于生活，又服务于生活。如何学好数学？这就要求我们要会用数学的眼光从生活中捕捉数学问题，自主运用数学知识分析生活现象，将生活问题抽象成数学问题，从而解决生活中的实际问题。那么，在运用一元二次方程解决实际问题的过程中，我们应找出问题中的已知量和未知量，分析数量之间的等量关系，建立数学模型，列出符合题意的方程，同时不忘检验方程的解是否合理。这样，问题便能迎刃而解，同时学习的知识也能形成体系。