异步电机矢量控制系统中自适应滑模变结构控制器研究

中国船舶第七一五研究所 张天俊

PI控制器是目前异步电机矢量控制系统中较通用的控制器。但异步电机的参数极易受到环境变化的影响，如果加入电机在线参数辨识又会增加系统的复杂性，不利于矢量控制变频器的实用化。本文采用积分型滑模变结构面和自适应控制律对转速控制器改进来减小转速的超调，提高系统的抗扰性。

1 自适应积分型滑模面变结构控制器的设计

滑模变结构控制(SMC)可以提高系统的鲁棒性和抗干扰性。系统但控制器若选用SMC会引入开关信号，易使系统不稳定且引入高频噪声。为此，本文在滑模面设计时选用积分型滑模面，可以很大程度上抑制噪声。此外，矢量控制中控制器设计依赖电机参数精度，尤其是电机的转动惯量J的误差直接影响系统性能。然而异步电机参数J的辨识实验要在电机转轴上安装定制的齿轮，操作复杂、辨识精度不高且难以测量其持续变化的量。因此，本文在设计转速控制器时引入自适应滑模控制律，将J作为系统未知量进行估算，仿真验证系统得到很好的控制性能。

1.1 积分型滑模面变结构控制器设计

转速控制器的状态变量为：

式中，ω*为给定转速，ω为实际转速。电机的运动方程为：

式中，Te为电磁转矩、TL为负载转矩、J为转动惯量。

本文设计系统的积分型滑模面s为：

选取上述滑模面积分的初始值为：

指数趋近律的形式如下：

式中，-ks为指数趋近项。采用饱和函数sat(s)替换式(5)中的符号函数，进一步削弱系统的抖振。选Te作为转速SMC的输出：

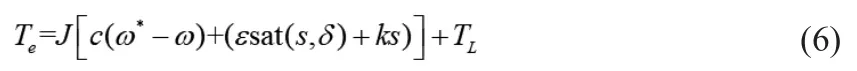
1.2 自适应滑模控制律的设计与分析

定义J的上下界为0≤Jmin≤J≤Jmax，取θ为J的估计值。令J1=θ-J，定义李雅普诺夫函数为：

经过整理则得到最终控制律：

选取自适应律如下：

V≥ 0且≤0，可知t→∞时，V有界，θ有界。但根据拉萨尔不变形定理1只能证明s→0，无法得到J1→0。为避免θ≤ 0或θ过大造成Te也过大，本文设计自适应律来确保θ∈[Jmin，Jmax]。

本文控制器参数如表1所示。

表1 控制器参数

2 基于改进的滑模变结构矢量控制系统仿真研究

异步电机的参数为：P=370W，f=50Hz，U=380V，I=1.05A，ω=1400r/min，Rs=14.96Ω，Rr=14.86Ω，Lls=96.72mH，Llr=109.49mH，Lm=829.49mH，J=0.004kg.m2。

如图1、2所示，给定转速为80rad/s空载启动，在1.5s时加入1N·m负载。当电机运行过程中突加负载，采用积分型滑模面SMC转速波动比PI控制器下小，且Te跟踪负载转矩更快。因此，积分型滑模面变结构控制器提高异步电机系统的启动性能与抗干扰性能。

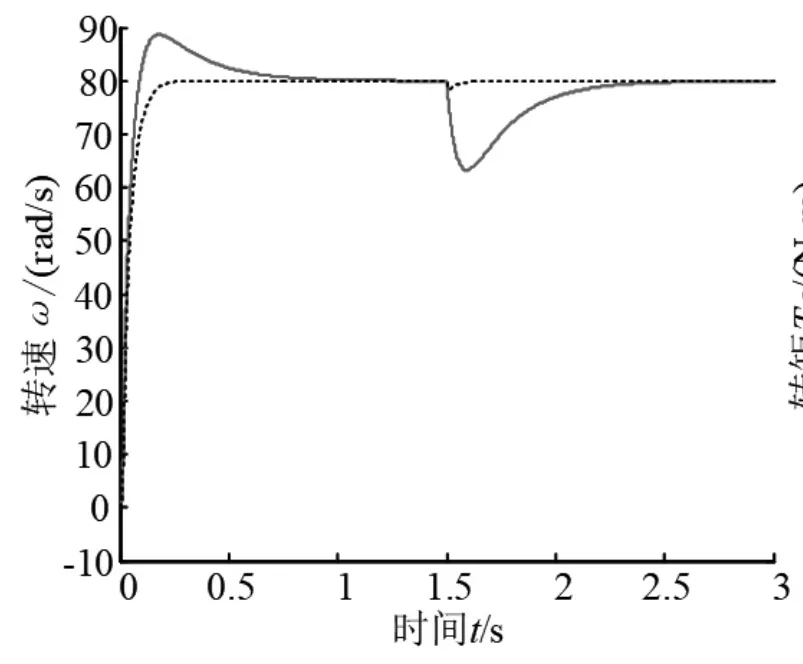
图1 突加负载时转速

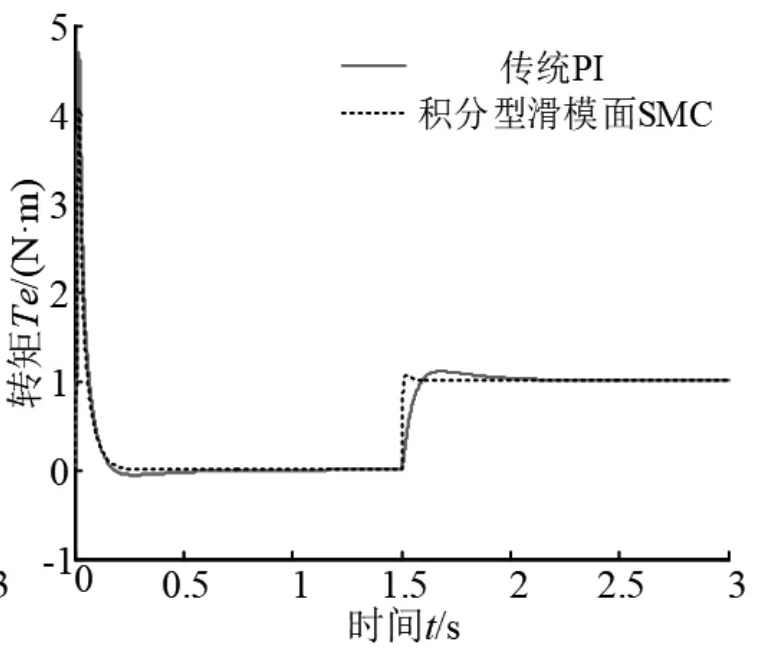
图2 突加负载时转矩

图4 自适应SMC转矩波形

将J的给定值在5s时间内从1-5倍按指数增长曲线连续变化，如图3、4所示，利用自适应积分型SMC的速度控制器，仍能保持系统的ω、Te可以很好的跟随给定。综上，本文所述方法在转速控制器上的应用提高了异步电动机矢量控制系统的鲁棒性与抗干扰性。

图3 自适应SMC转速波形